STL庫——二叉搜索樹

? ? ? ? ?

づ?ど

?🎉?歡迎點贊支持🎉

個人主頁：勵志不掉頭發的內向程序員；

專欄主頁：C++語言；

文章目錄

前言

一、二叉搜索樹的概念

二、二叉搜索樹的性能分析

三、二叉搜索樹的插入

四、二叉搜索樹的查找

五、二叉搜索樹的刪除

六、二叉搜索樹的析構

七、二叉搜索樹的拷貝

八、二叉搜索樹 key 和 key/value 使用場景

6.1、key搜索場景

6.2、key/value 搜索場景：

6.3、key/value 二叉搜索樹代碼實現

總結

前言

這一章節我們來聊聊我們之前的二叉樹的一種新形態二叉搜索樹，這個形態也有一定的問題，但是它是我們后面講解 map/set 容器的基礎，我們到后面才會講解改怎么解決二叉搜索樹的方式，但是我們本章節搞明白二叉搜索樹的原理和實現也非常重要。

一、二叉搜索樹的概念

二叉搜索樹又稱二叉排序樹，它要么是一顆空樹，要么是具有以下性質的二叉樹：

若它的左子樹不為空，則左子樹上所有結點的值都小于等于根結點的值。
若它的右子樹不為空，則右子樹上所有結點的值都大于等于根節點的值。
它的左右子樹也分別為二叉搜索樹。
二叉搜索樹中可以支持插入相等的值，也可以不支持插入相等的值，具體看使用場景定義，后續我們學習 map/set/multimap/multiset 系列容器底層就是二叉搜索樹，其中 map/set 不支持插入相等值，multimap/multiset 支持插入相等值。

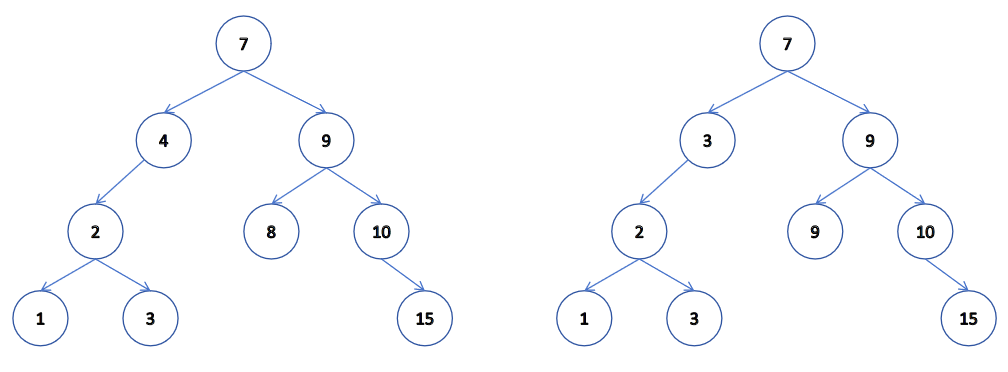
我們二叉樹的邏輯就是，當插入一個新結點時，從頭結點，也就是樹的根結點開始做比較，如果比新結點大，就走到我們的右結點。如果比新小節點小，就走到我們的左節點，然后再和這些結點進行比較，一直到結點走到底，沒有結點比較時就插入即可。

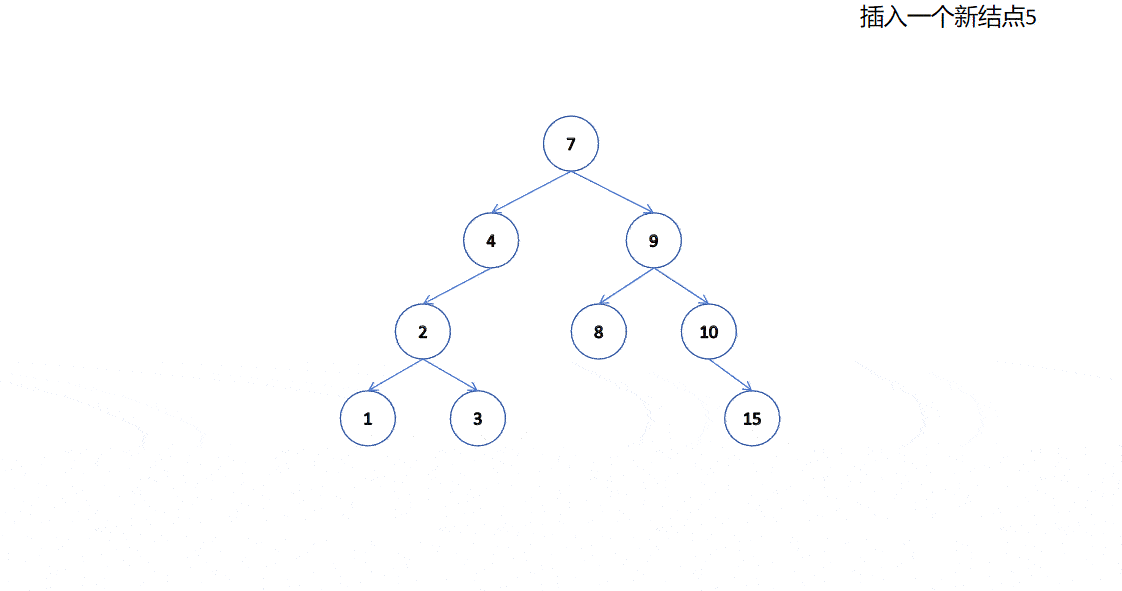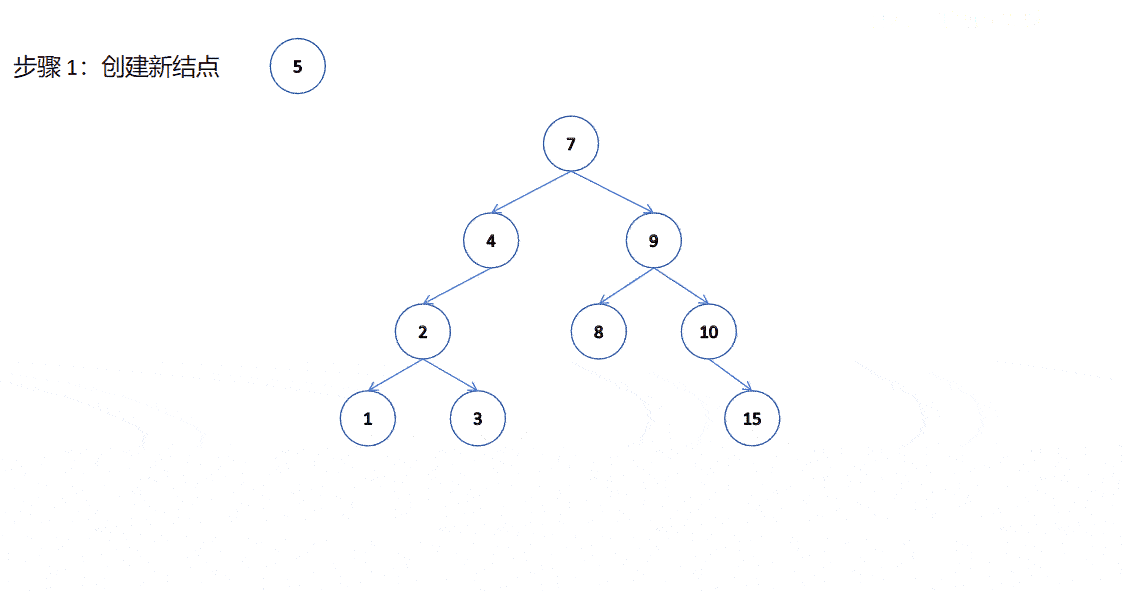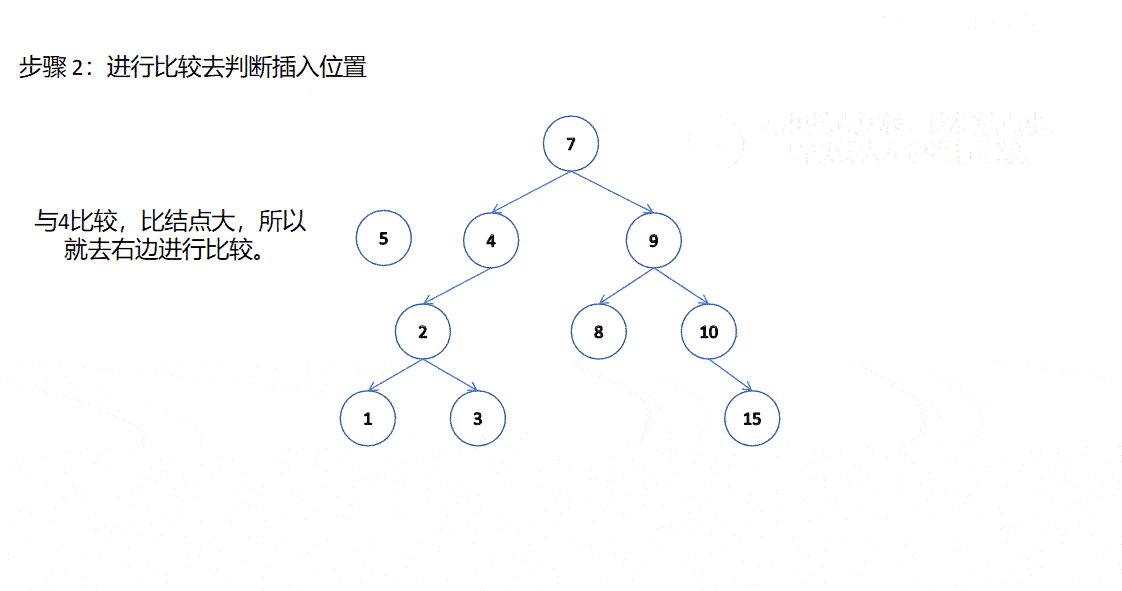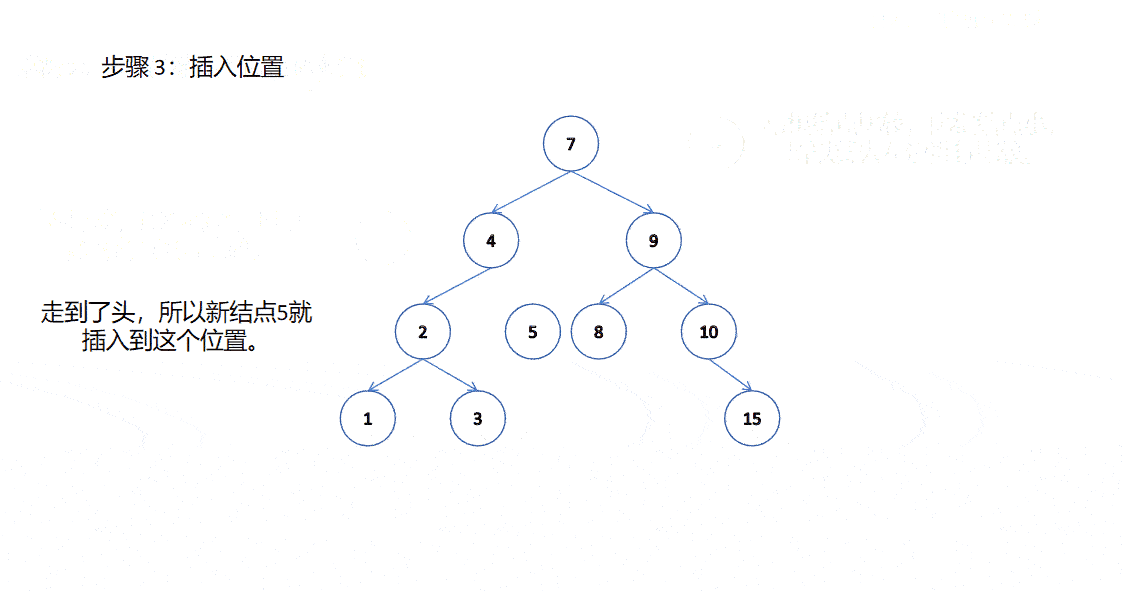
我們學習數據結構的時候可能有聽說過我們二叉樹如果單獨存儲數據是沒有意義的。要想有意義，我們得在二叉樹的基礎上加入一些東西，這樣才有意義，就比如在二叉樹的基礎上加入搜索二叉樹的規則。

二、二叉搜索樹的性能分析

最優情況下，二叉搜索樹為完全二叉樹（或者接近完全二叉樹），其高度為：log2(N)。

最差情況下，二叉樹退化為單支樹（或者類似單支），其高度為：N。

所以綜合而言二叉搜索樹增刪查改時間復雜度為：O(N)。

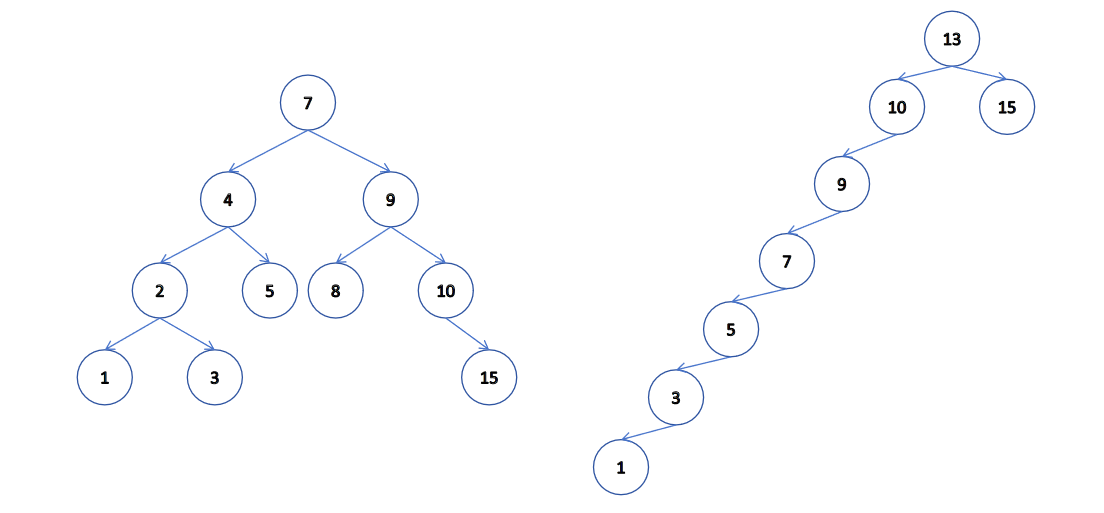
這樣的效率顯然是無法滿足我們需求的，我們后面章節會繼續講解二叉搜索樹的變形，平衡二叉搜索樹AVL樹和紅黑樹，才能適用于我們在內存中存儲和搜索數據。

另外，我們二分查找也可以實現 O( log2(N) ) 級別的查找效率，但是二分查找有兩大缺陷：

需要存儲在支持下標隨機訪問的結構中，并且有序。
插入和刪除數據效率很低，因為存儲在下標隨機訪問的數據結構中，插入和刪除數據一般需要挪動數據。

三、二叉搜索樹的插入

插入的具體過程如下：

樹為空，則直接新增結點，賦值給 root 指針。
樹不為空，按二叉搜索樹性質，插入值比當前結點大往右走，插入值比當前結點小往左走，找到空位置，插入新結點。
如果支持插入相等的值，插入值跟當前結點相等的值可以往右走，也可以往左走，找到空位置，插入新結點（要注意的是要保持邏輯一致性，插入相等的值不要一會兒往左走，一會兒往右走）。

就如上圖一樣的插入方式。

我們先把二叉搜索樹的框架搭建出來，創建一個結點類，這個結點包含左結點的指針和右結點的指針，以及一個要保存的類型。

namespace zxl
{template <class K>struct BSTNode{BSTNode<K>* _left;BSTNode<K>* _right;K _key;BSTNode(const K& key): _key(key),_left(nullptr),_right(nullptr){}};template <class T>class BSTree{typedef BSTNode<T> Node;public:private:Node* _root = nullptr;};
}

我們設計一個插入的成員函數，它的返回值可以是布爾類型來查看是否插入成功。我們可以通過while 循環比較的方式一直比較到 nullptr 時讓循環停下來，但是此時我們的 cur 指向的是一個空指針，我們應該指向它的上一個指針，所以我們還得創建一個變量來記錄上一個變量，通過 cur 的上一個變量來插入我們的新結點。我們這里實現的是不允許有相等的情況出現的，如果想要實現有相等的情況可以在比較那里改一下即可。

我們可以來看看下面的動畫來幫助理解。

bool insert(const T& key)
{if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;
}

此時我們可以寫一個中序遍歷來看看我們實現的怎么樣，由于我們的二叉搜索樹的結構，這導致我們的中序遍歷出來的是一個從小到大排序好的數據，這樣就可以驗證我們的插入實現的是否成功。

我們把中序遍歷寫在私有位置，這樣就可以不把根結點暴露出去。我們想要調用遞歸，就必須傳Node 的指針，如果我們把我們的中序遍歷寫在公有，那它有默認的 this 指針，可以調用 _root，但是此時去下一層就得傳下一層的地址，但是由于我們之前是靠 this 指針而得到的 _root。所以此時我們就無法傳值到遞歸下一層。但是如果我們想要寫一個傳值的成員函數，不寫在私有的話因為要傳指針所以就得暴露我們的 _root。所以為了避免我們干脆直接寫成私有的。

private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}

此時我們就有一個問題，那就是我們在外界沒辦法調用我們的中序遍歷，此時我們可以在類內公有位置創建一個成員函數，讓這個成員函數去調用我們的中序遍歷即可。

public:void InOrder(){_InOrder(_root);cout << endl;}

此時我們就可以嘗試去測試我們的插入了。

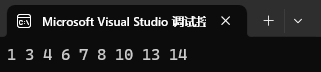
int main()
{zxl::BSTree<int> t;int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };for (int i = 0; i < sizeof(a) / sizeof(int); i++){t.insert(a[i]);}t.InOrder();return 0;
}

四、二叉搜索樹的查找

我們查找的邏輯就和搜索的邏輯一樣。

從根開始比較，查找 x，x 比根的值大則往右邊查找，x 比根小則往左邊查找。
最多查找高度次，走到空還沒找到這個值就不存在。
如果不支持插入相等的值，找到 x 即可返回。
如果支持插入相等的值，意味著有多個 x 存在，一般要求查找中序的第一個 x。

bool Find(const T& key)
{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;
}

五、二叉搜索樹的刪除

首先查找元素是否在二叉搜索樹中，如果不存在，則返回 false。

如果查找元素存在則分以下四種情況分別處理：（假設要刪除的結點為 N）

要刪除結點 N 左右孩子結點均為空。
要刪除結點 N 左孩子結點為空，右孩子結點不為空。
要刪除結點 N 右孩子結點為空，左孩子結點不為空。
要刪除結點 N 左右孩子結點均不為空。

第一種情況：

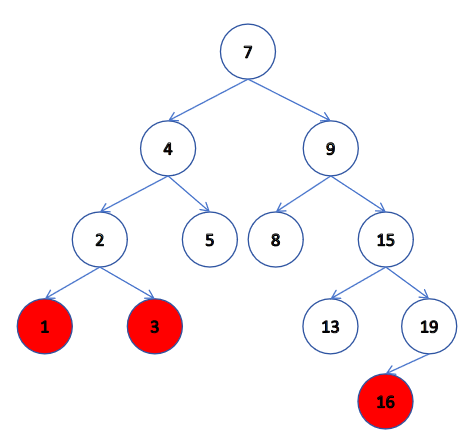
第二種情況：

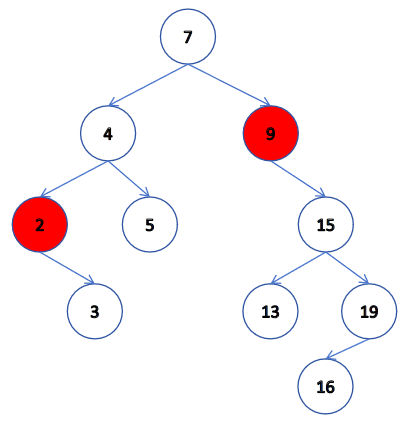
第三種情況：

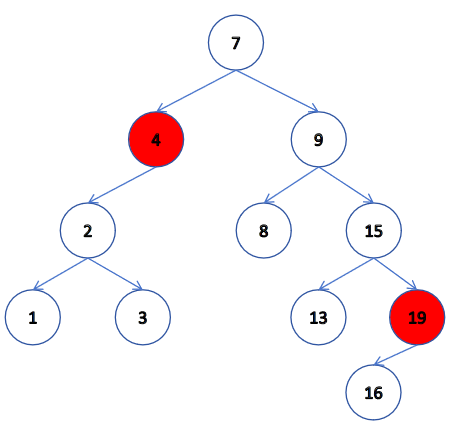
第四種情況：

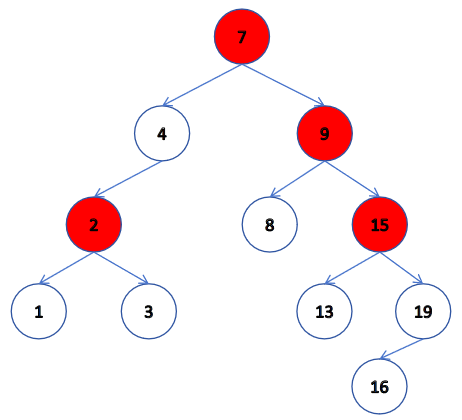
對應以上四種情況的解決方案：

由于 N 結點左右孩子都是空，所以我們直接銷毀掉我們的這個結點即可，但是為了讓它的父親結點不會指向野指針，我們在銷毀這個結點后要記得把指向它的父親結點指向 nullptr。
把N結點的父親對應孩子指針指向N的右孩子，然后就像 1 一樣刪除掉 N 結點即可。
把N結點的父親對應孩子指針指向N的左孩子，然后就像 1 一樣刪除掉 N 結點即可。
無法直接刪除 N 結點，因為 N 的兩個孩子無處安放，只能用替換法刪除。找 N 左子樹的值最大結點 R（最右結點）或者?N 右子樹的值最小結點 L（最左結點）代替 N，因為這兩個結點中任意一個，放到 N 的位置，都滿足二叉搜索樹的規則。替代 N 的意思就是 N 和 R 的兩個結點的值的交換，轉而變成刪除 R 結點，R 結點符號情況 2 或情況 3，可以直接刪除。

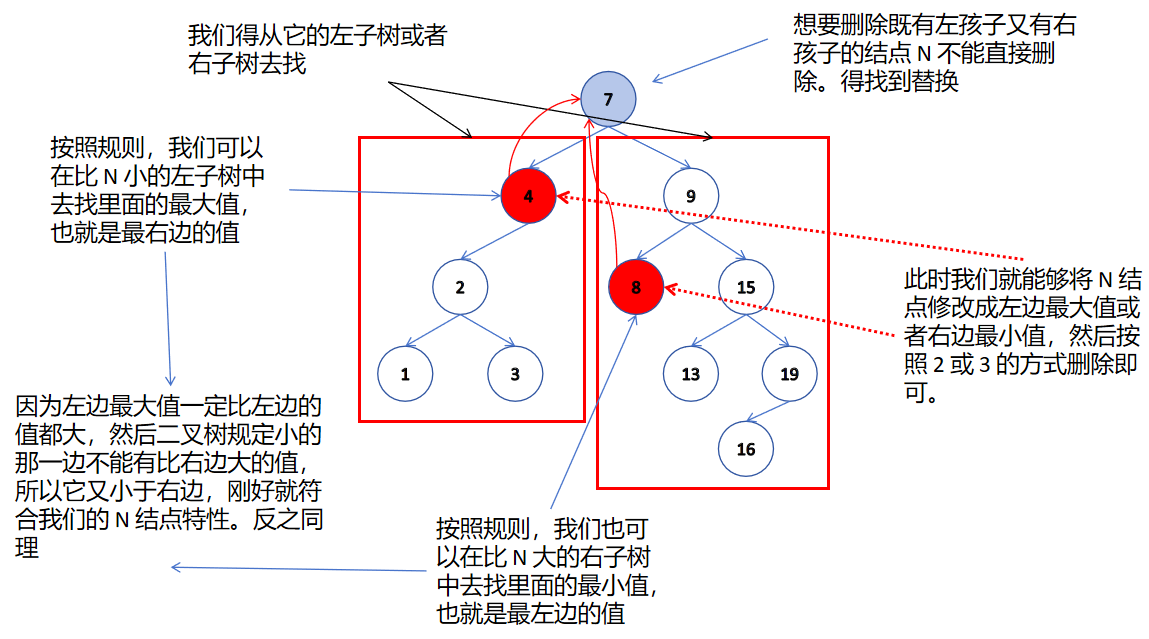
我們先用循環去找到我們的 key 值，邏輯和上面一樣，當我們的找到我們 key 時，我們就開始討論這 4 種情況，我們的情況 1 其實可以融合在情況 2 或 3中，所以這里就只討論 3 種情況。

第一種情況：

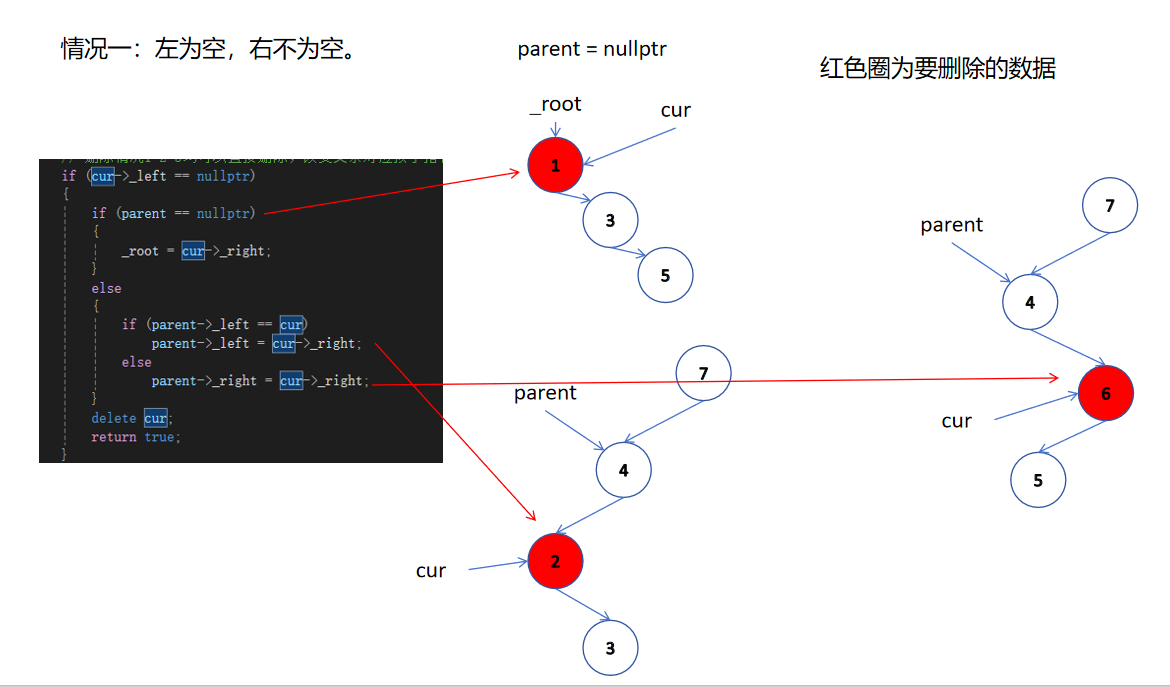
第二種情況：

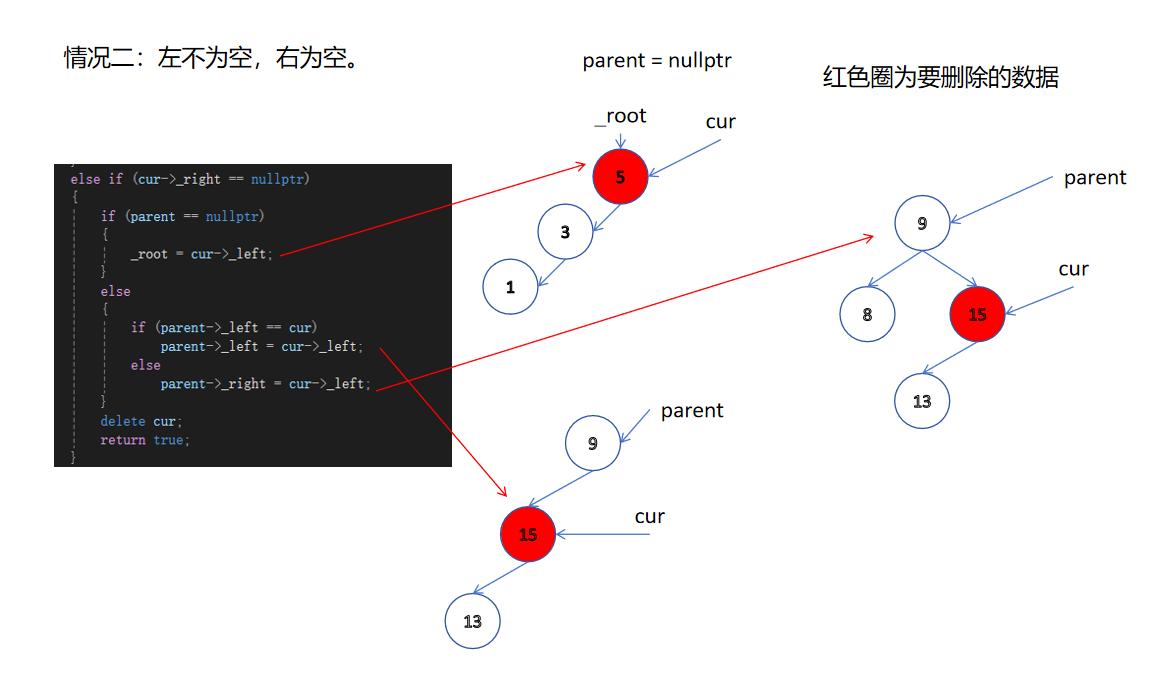
bool Erase(const T& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 0-1個孩?的情況// 刪除情況1 2 3均可以直接刪除，改變?親對應孩?指針指向即可if (cur->_left == nullptr){if (parent == nullptr){_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;return true;}else if (cur->_right == nullptr){if (parent == nullptr){_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;return true;}else{// 2個孩?的情況// 刪除情況4，替換法刪除// 假設這?我們取右?樹的最?結點作為替代結點去刪除// 這?尤其要注意右?樹的根就是最?情況的情況的處理，// 對應課件圖中刪除7的情況// ?定要把cur給rightMinP，否會報錯。Node* rightMinP = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinP = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;if (rightMinP->_left == rightMin)rightMinP->_left = rightMin->_right;elserightMinP->_right = rightMin->_right;delete rightMin;return true;}}}return false;
}

六、二叉搜索樹的析構

我們二叉搜索樹的析構可以使用遞歸，向我們的中序遍歷一樣得讓遞歸函數私有，然后再在公有的地方實現析構函數以此來保護我們的根結點。

public:~BSTree(){Destroy(_root);_root = nullptr;}private:void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}

七、二叉搜索樹的拷貝

和我們的析構同理，也是用遞歸來實現。

public:BSTree(const BSTree<K, V>& t){_root = Copy(t._root);}private:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key, root->_value);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}

剩下的像默認構造沒有必要實現，而賦值重載用我們的交換大法即可輕松完成，這里就不過多贅述。

八、二叉搜索樹 key 和 key/value 使用場景

6.1、key搜索場景

只有 key 作為關鍵碼，結構中只需要存儲 key 即可，關鍵碼即為需要搜索到的值，搜索場景只需要判斷 key 在不在。key 的搜索場景實現的二叉樹搜索樹支持增刪查，但是不支持修改，修改 key 破壞搜索樹機構了。

場景1：小區無人值守車庫，小區車庫買了車位的業主車才能進小區，那么物業會把買了車位的業主的車牌號錄入后臺系統，車輛進入時掃描車牌在不在系統中，在則抬桿，不在則體現非本小區車輛，無法進入。

場景2：檢查一篇英文文檔拼寫是否正確，將詞庫中所有的單詞放入二叉搜索樹，讀取文章中的單詞，查找是否在二叉搜索樹中，不在則波浪線標紅提示。

6.2、key/value 搜索場景：

每?個關鍵碼 key，都有與之對應的值 value，value 可以任意類型對象。樹的結構中 (結點) 除了需要存儲 key 還要存儲對應的 value，增/刪/查還是以 key 為關鍵字??叉搜索樹的規則進行比較，可以快速查找到 key 對應的 value。key/value 的搜索場景實現的?叉樹搜索樹?持修改，但是不?持修改 key，修改 key 破壞搜索樹性質了，可以修改 value。

場景1：簡單中英互譯字典，樹的結構中 (結點) 存儲 key (英?) 和 vlaue (中?)，搜索時輸入英?，則同時查找到了英?對應的中?。

場景2：商場無人值守車庫，入口進場時掃描車牌，記錄?牌和入場時間，出口離場時，掃描車牌，查找入場時間，?當前時間 - 入場時間計算出停車時長，計算出停?費?，繳費后抬桿，車輛離場。

場景3：統計?篇?章中單詞出現的次數，讀取?個單詞，查找單詞是否存在，不存在這個說明第?次出現，（單詞，1），單詞存在，則++單詞對應的次數。

6.3、key/value 二叉搜索樹代碼實現

我們 key/value 的結構和我們上面的 key 結構相比，無非就是多了一個 value，我們在結點創建時多創建一個 value，然后在增刪查的時候我們只要讓我們傳過來的值中的 key 進行比較，然后 value 不管，插入時把 key/value 都插入即可實現，我們可以通過下面的 key/value 的代碼和上面的 key 作比較就能看出其中的相似。

namespace zxl
{template<class K, class V>struct BSTNode{// pair<K, V> _kv;K _key;V _value;BSTNode<K, V>* _left;BSTNode<K, V>* _right;BSTNode(const K& key, const V& value):_key(key), _value(value), _left(nullptr), _right(nullptr){}};template<class K, class V>class BSTree{typedef BSTNode<K, V> Node;public:BSTree() = default;BSTree(const BSTree<K, V>& t){_root = Copy(t._root);}BSTree<K, V>& operator=(BSTree<K, V> t){swap(_root, t._root);return *this;}~BSTree(){Destroy(_root);_root = nullptr;}bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{if (cur->_left == nullptr){if (parent == nullptr){_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;return true;}else if (cur->_right == nullptr){if (parent == nullptr){_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;return true;}else{Node* rightMinP = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinP = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;if (rightMinP->_left == rightMin)rightMinP->_left = rightMin->_right;elserightMinP->_right = rightMin->_right;delete rightMin;return true;}}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key, root->_value);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}private:Node* _root = nullptr;};}