基于偏最小二乘法（PLS）多輸入單輸出的回歸預測【MATLAB】

在科學研究和工程實踐中，我們常常需要根據多個相關變量來預測一個關鍵結果。例如，根據氣溫、濕度、風速等多個氣象因素預測空氣質量指數，或根據多種原材料成分預測產品的最終性能。這類“多輸入單輸出”的預測任務，對模型處理復雜變量關系的能力提出了挑戰。本文將介紹一種經典且高效的統計建模方法——偏最小二乘法（Partial Least Squares, PLS），并展示如何在MATLAB中利用它實現精準的回歸預測。

為什么選擇偏最小二乘法（PLS）？

在處理多輸入數據時，變量之間往往存在高度相關性（即共線性），或者輸入變量的數量遠超樣本數量，這會使傳統回歸方法（如多元線性回歸）失效或表現不佳。偏最小二乘法正是為解決這類問題而設計的。

PLS的核心優勢在于它能夠：

• 有效處理共線性：即使輸入變量之間高度相關，PLS也能穩定地提取信息，避免模型崩潰。
• 降維與信息融合：它不直接使用原始變量，而是通過分析輸入與輸出之間的關系，構建出一組新的、互不相關的“綜合變量”（也稱潛變量或主成分）。這些綜合變量集中了原始數據中的關鍵信息，同時大幅降低了數據的復雜度。
• 兼顧輸入與輸出的關系：與主成分分析（PCA）只關注輸入數據的方差不同，PLS在提取綜合變量時，會同時考慮這些變量對輸出目標的預測能力，確保降維過程“有的放矢”。

因此，PLS特別適合于變量多、相關性強、樣本量有限的復雜預測場景。

PLS的工作原理（直觀理解）

可以將PLS的運作過程想象成一場“信息提煉”之旅：

1. 尋找最佳“投影方向”：PLS首先在輸入數據中尋找一個方向，使得沿著這個方向投影后得到的“綜合變量”，既能最大程度地概括輸入數據的變化，又能最好地解釋輸出變量的變化。
2. 提取第一對“潛變量”：根據找到的方向，計算出輸入數據的第一個“綜合變量”和對應的輸出“綜合變量”。這兩個變量共同捕捉了數據中最核心的預測信息。
3. 剝離已提取信息：將原始數據中已經被這對“潛變量”解釋的部分剔除，得到“殘差數據”。
4. 重復過程：在殘差數據上重復上述步驟，尋找下一個最佳方向，提取第二對潛變量。這個過程可以持續進行，直到提取出足夠數量的潛變量，或者模型性能不再顯著提升。
5. 建立預測模型：最終，PLS將這些潛變量與原始輸出變量建立回歸關系。當有新的輸入數據時，模型會先將其轉換為對應的潛變量，再通過回歸方程預測出最終的輸出結果。

整個過程自動化地完成了從高維、相關數據中提取關鍵預測因子，并建立簡潔高效模型的任務。

MATLAB實現步驟

在MATLAB中實現PLS回歸預測非常便捷，主要依賴其內置的統計和機器學習工具。以下是關鍵步驟：

1. 數據準備：

   • 使用 readtable 或 xlsread 等函數加載數據。
   • 將數據劃分為訓練集和測試集（可使用 cvpartition）。
   • 對輸入和輸出數據進行歸一化處理（mapminmax 函數），這是PLS的標準預處理步驟。

2. 模型訓練：

   • 調用 plsregress 函數，輸入訓練集的輸入矩陣和輸出向量。
   • 指定需要提取的潛變量數量。這個數量可以通過交叉驗證（Cross-Validation）來確定，以避免過擬合。plsregress 函數會返回模型系數、得分、載荷等關鍵信息。

3. 模型驗證與潛變量選擇：

   • 利用交叉驗證結果，繪制預測誤差隨潛變量數量變化的曲線。
   • 選擇誤差最小或趨于穩定的潛變量數量，作為最終模型的配置。

4. 預測與評估：

   • 使用訓練好的模型對測試集進行預測。
   • 計算預測性能指標，如決定系數（R2）、均方根誤差（RMSE）等，評估模型的準確性。
   • 使用 plot 函數繪制預測值 vs. 真實值的散點圖，直觀檢驗模型效果。

應用場景

偏最小二乘法在眾多領域都有廣泛應用：

• 化學與制藥：光譜數據分析（如近紅外、拉曼光譜），根據光譜特征預測物質濃度或成分。
• 生物醫學：基因表達數據分析，預測疾病狀態或治療反應。
• 工業過程控制：根據多個傳感器讀數預測關鍵產品質量指標。
• 社會科學：分析調查問卷數據，預測用戶滿意度或行為傾向。

優勢與注意事項

優勢：

• 算法成熟穩定，理論基礎扎實。
• 特別擅長處理小樣本、多變量、高共線性的數據。
• 模型具有較好的可解釋性，可通過載荷分析了解各輸入變量的重要性。

注意事項：

• 數據標準化是必要步驟。
• 潛變量數量的選擇至關重要，需通過交叉驗證等方法謹慎確定。
• 主要適用于線性或近似線性關系；對于強非線性問題，可考慮結合核方法或其他非線性模型。

結語

偏最小二乘法（PLS）作為一種強大的多變量分析工具，在多輸入單輸出回歸預測任務中表現出色。它巧妙地解決了高維數據帶來的共線性和維度災難問題，通過提取關鍵潛變量，構建出簡潔而高效的預測模型。借助MATLAB強大的數據處理和統計分析功能，研究人員和工程師可以輕松實現PLS模型，快速從復雜數據中挖掘價值，為科學決策和工程優化提供有力支持。無論是初學者還是資深從業者，PLS都是一項值得掌握的重要技能。

部分代碼

%% 清空環境
warning off;          % 關閉警告提示
clc;                  % 清空命令行
clear;                % 清除工作區變量
close all;            % 關閉所有圖形窗口%% 讀取數據
res = xlsread('data.xlsx');  % 假設最后一列為輸出（標簽），其余為輸入（特征）
fprintf('數據已加載，共 %d 個樣本，%d 個特征。\n', size(res,1), size(res,2)-1);%% 劃分訓練集和測試集
train_ratio = 0.7;            % 訓練集占比
n = size(res, 1);             % 總樣本數
trainnum = floor(train_ratio * n);  % 訓練樣本數量
idx = randperm(n);            % 隨機打亂索引% 提取訓練集（輸入 P，輸出 T），并轉置為 【特征×樣本】格式
P_train = res(idx(1:trainnum), 1:end-1)';  % 輸入：前若干列為特征
T_train = res(idx(1:trainnum), end)';      % 輸出：最后一列為目標值
M = size(P_train, 2);                      % 訓練樣本個數% 提取測試集
P_test = res(idx(trainnum+1:end), 1:end-1)'; % 測試輸入
T_test = res(idx(trainnum+1:end), end)';     % 測試輸出
N = size(P_test, 2);                         % 測試樣本個數fprintf('訓練集大小: %d 個樣本\n', M);
fprintf('測試集大小: %d 個樣本\n', N);%% 數據歸一化 [0,1]
% 對輸入和輸出分別進行歸一化，并保存參數用于反歸一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);% 轉置為【樣本×特征】格式，適配 plsregress 函數輸入要求
p_train = p_train';
p_test  = p_test';
t_train = t_train';
t_test  = t_test';

運行結果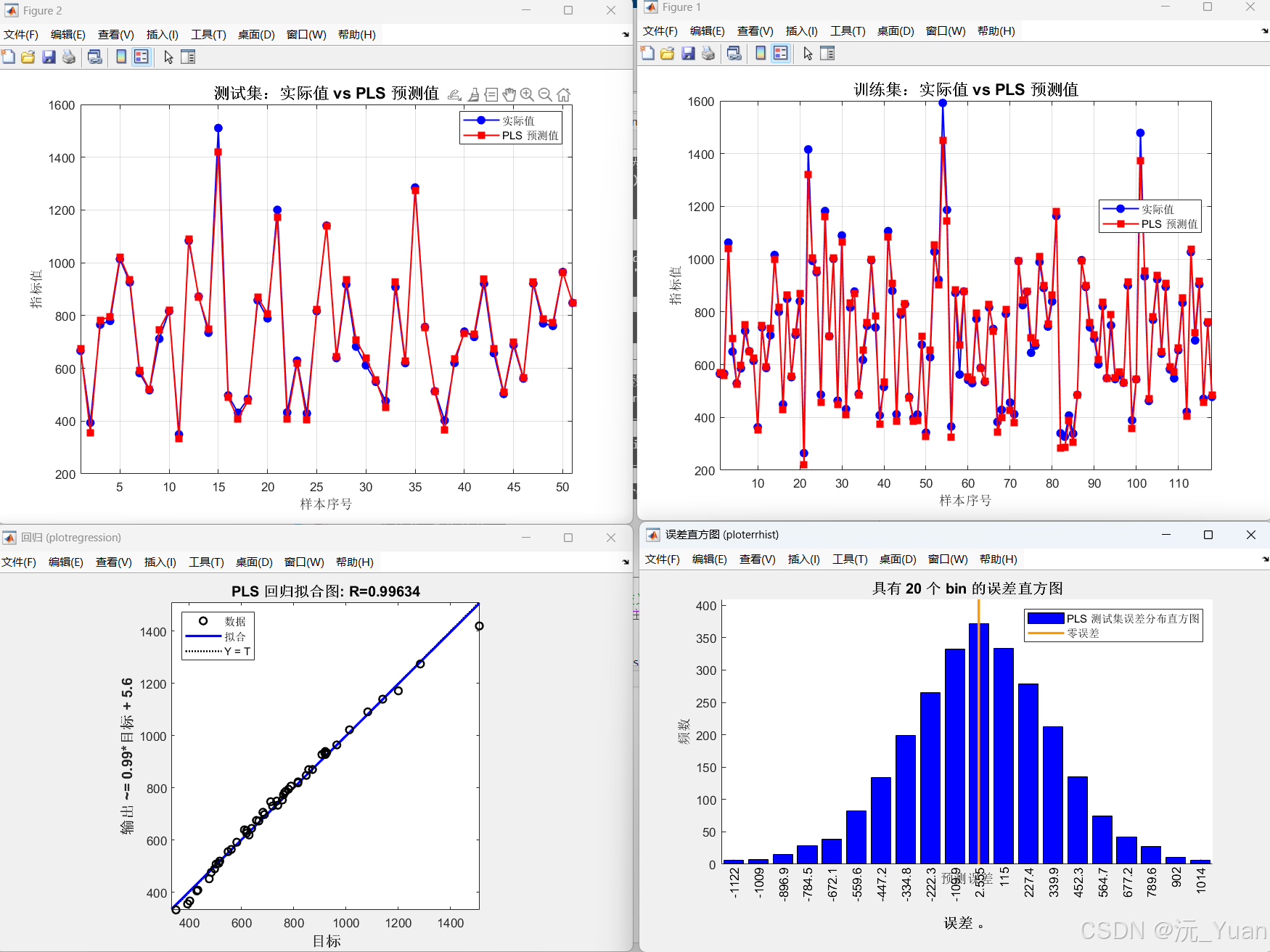

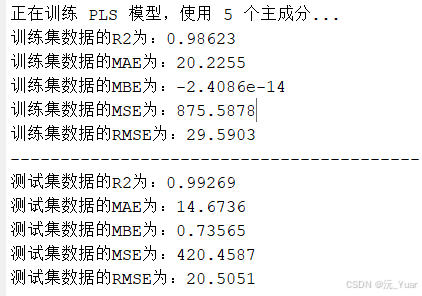
代碼下載

https://mbd.pub/o/bread/YZWXlJhvaA==