---

---

? 🎁個人主頁：工藤新一1

? 🔍系列專欄：C++面向對象（類和對象篇）

? 🌟心中的天空之城，終會照亮我前方的路

? 🎉歡迎大家點贊👍評論📝收藏?文章

---

二叉樹

一、二叉樹的概念與結構

• 樹是一種遞歸的結構

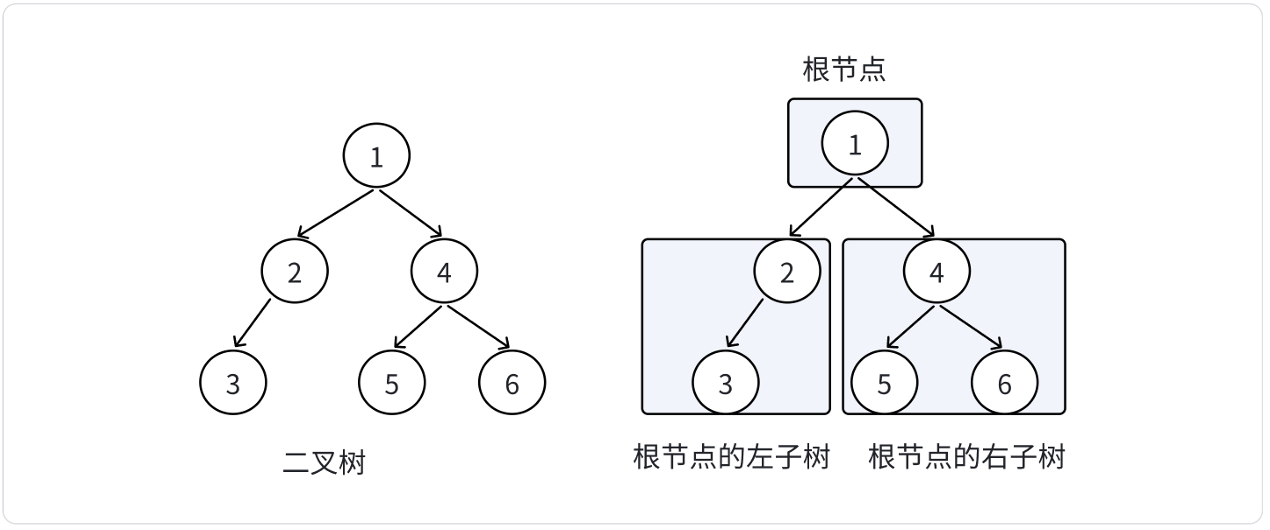
• 在樹形結構中，我們最常用的就是二叉樹。一顆二叉樹的節點是一個有限的集合，該集合由一個根節點，再加上兩顆別稱為左子樹和右子樹的二叉樹組成

---

---

二、幾種常見的樹

2.1二叉樹、滿二叉樹

• 二叉樹不存在 “度” 大于 2 的節點

• 二叉樹的子樹一定有序（有左右之分），次序不能顛倒，因此二叉樹是一顆有序樹

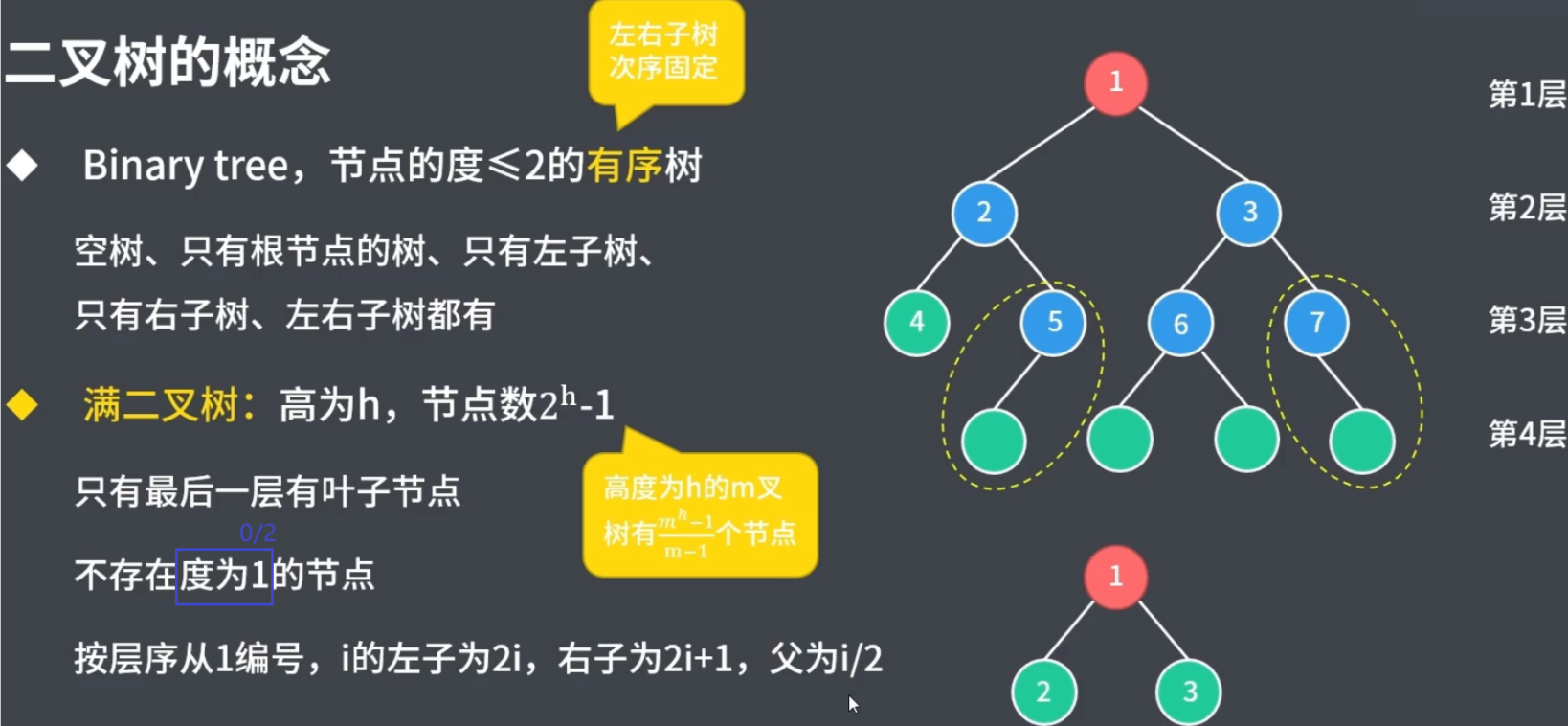
• 滿二叉樹（理想化的二叉樹）： 二叉樹的每一層的節點達到最大值，也就是說，如果一個二叉樹的層數為 K ，那么其總節點數是 2^k - 1，則其就為滿二叉樹

---

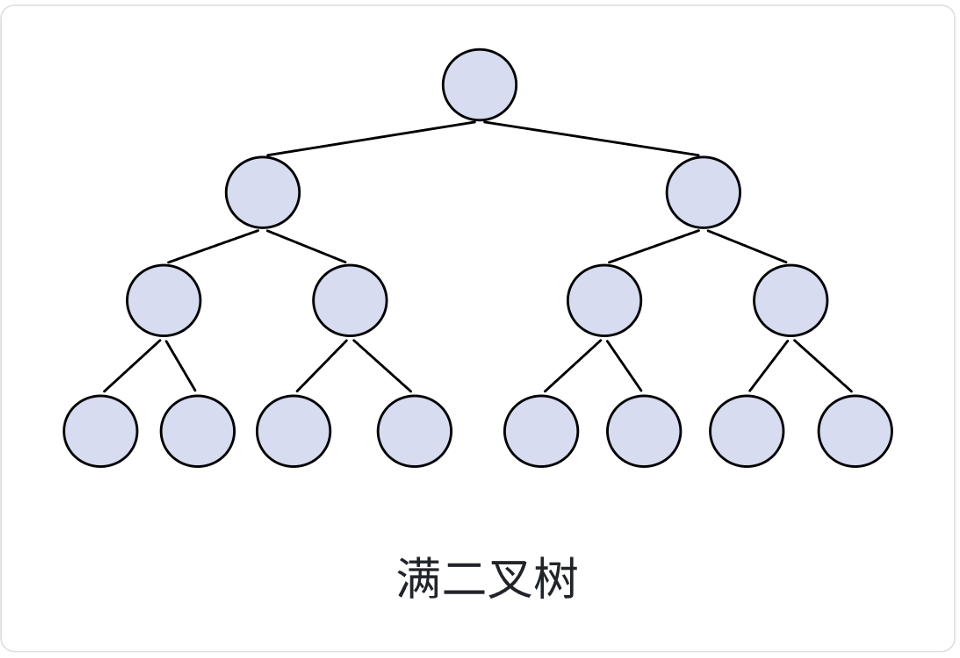
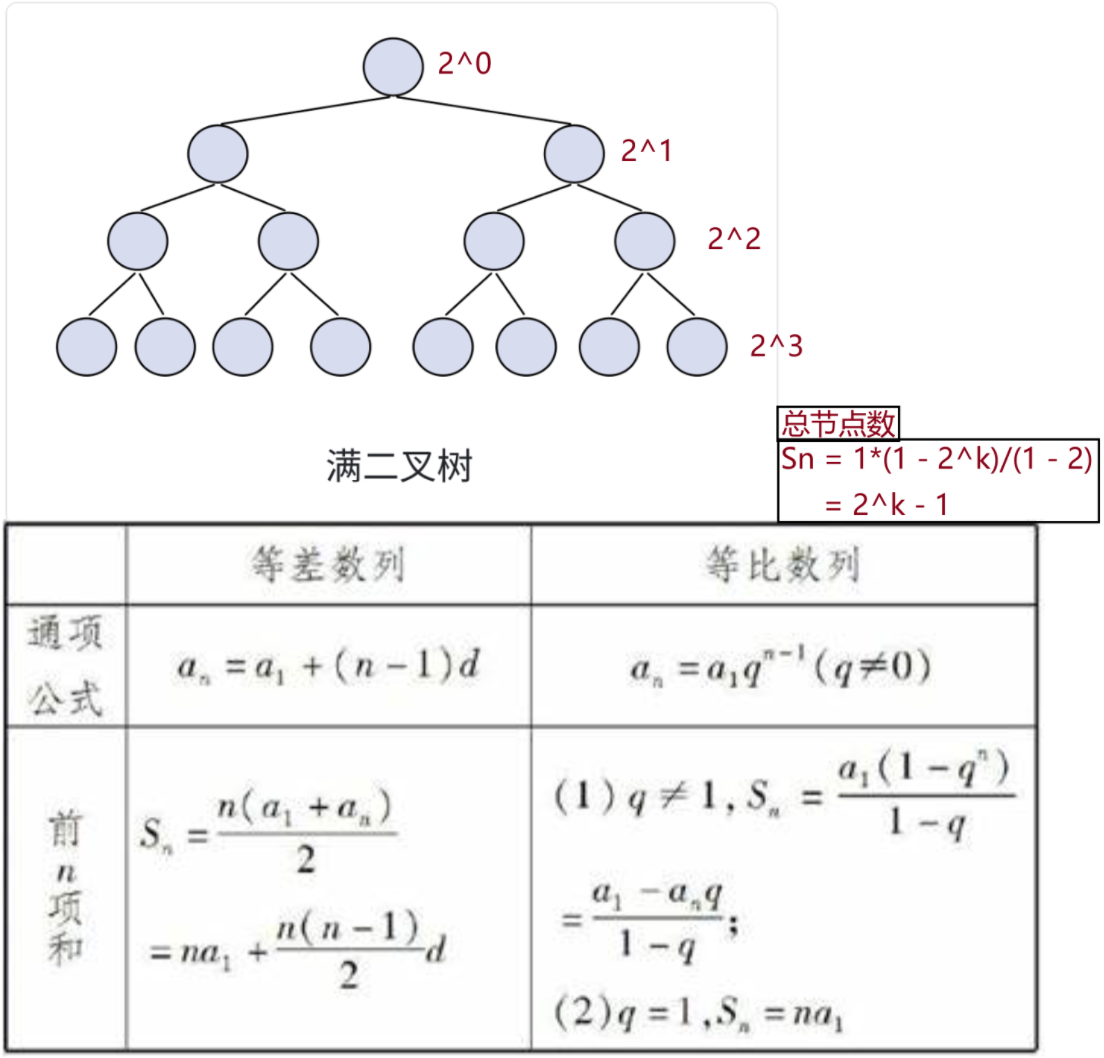
• 滿二叉樹：第 K 層節點個數是 2^k-1

---

2.2完全二叉樹

• 滿二叉樹是完全二叉樹中的子集（滿二叉樹是（特殊的）完全二叉樹），其是一個效率很高的數據結構

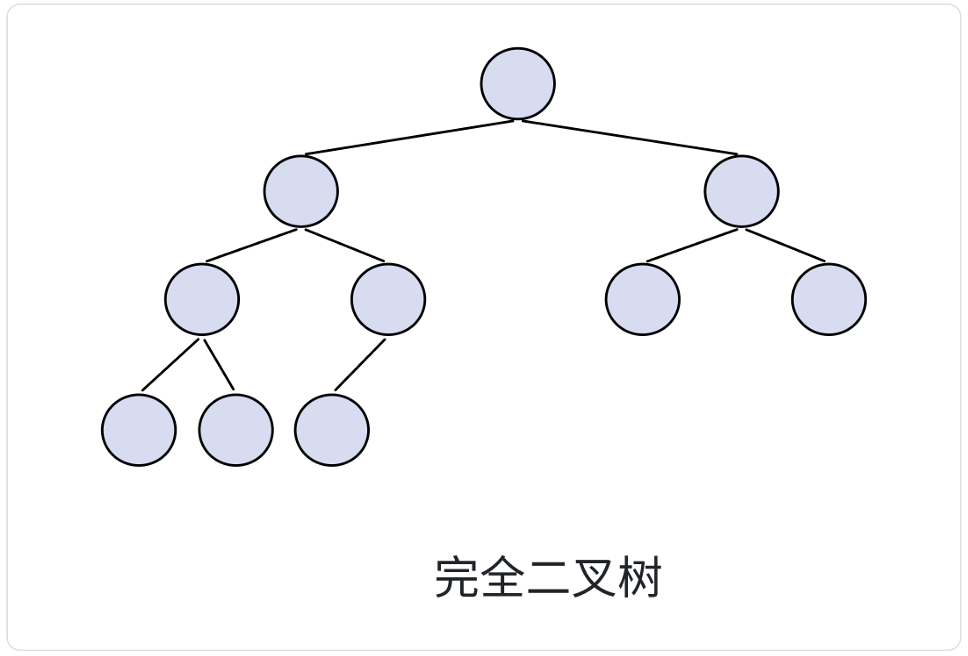
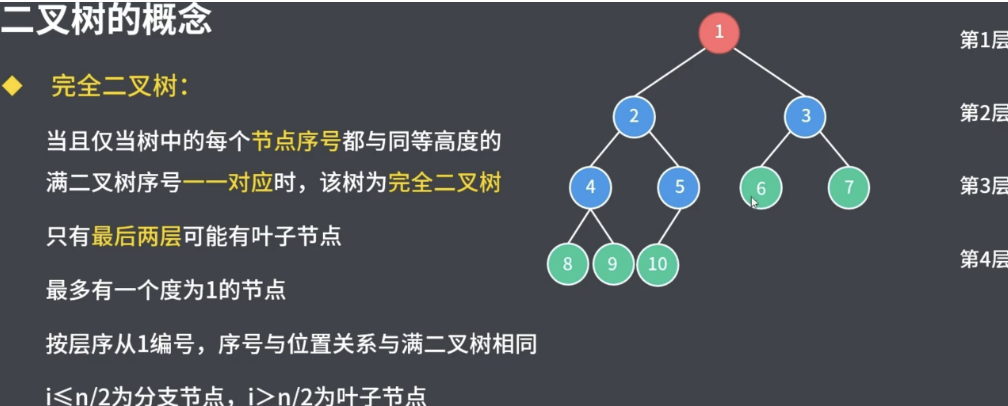
對于深度為 K ，有 n 個節點的二叉樹，當且僅當其每一個節點都與深度為 K 的滿二叉樹中編號從 1 到 n 的節點一 一對應時（節點從左到右依次排列）稱之為完全二叉樹。

• 最后一層節點個數未達到最大：完全二叉樹
• 最后一層節點個數達到最大：即是完全二叉樹，又是滿二叉樹

---

---

---

• 完全二叉樹

---

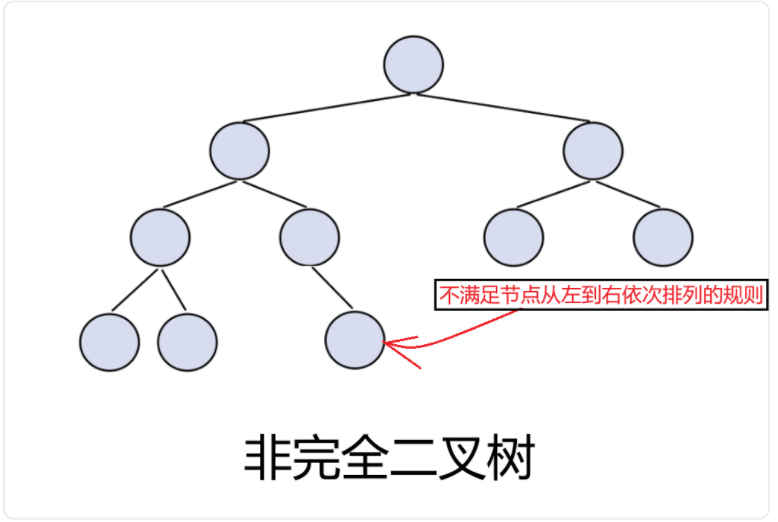
• 非完全二叉樹

---

---

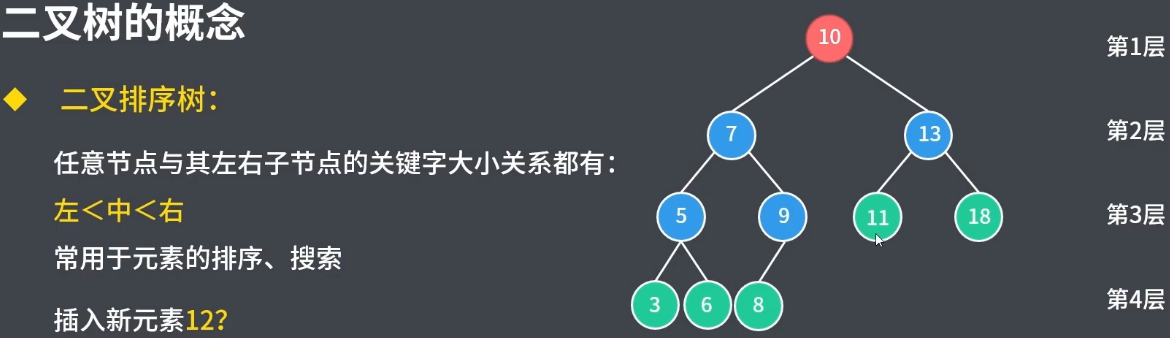
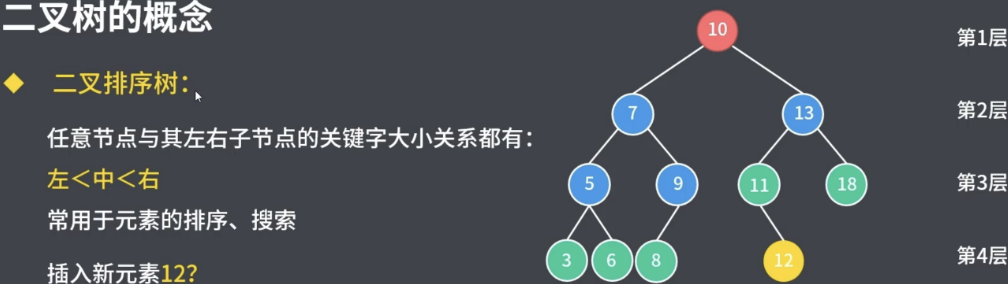
2.3二叉排序樹

常用于非重復元素的排序、搜索；對二叉排序樹進行左中右遍歷可以獲取到有序的元素串

---

---

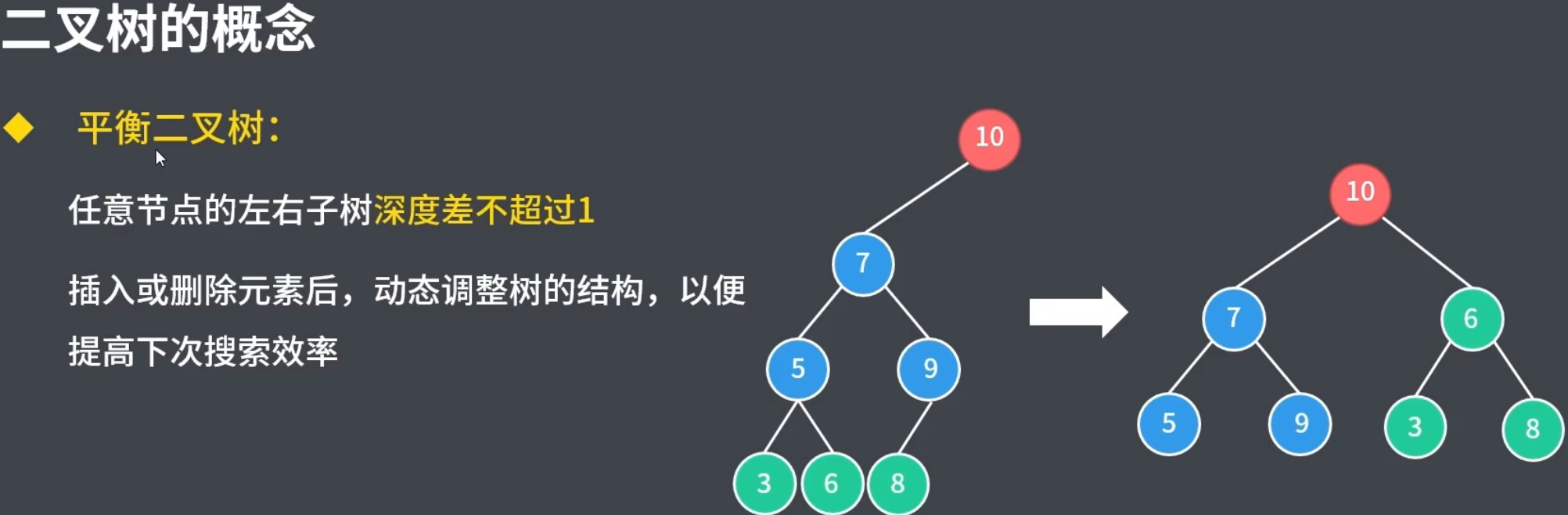
2.4平衡二叉樹

---

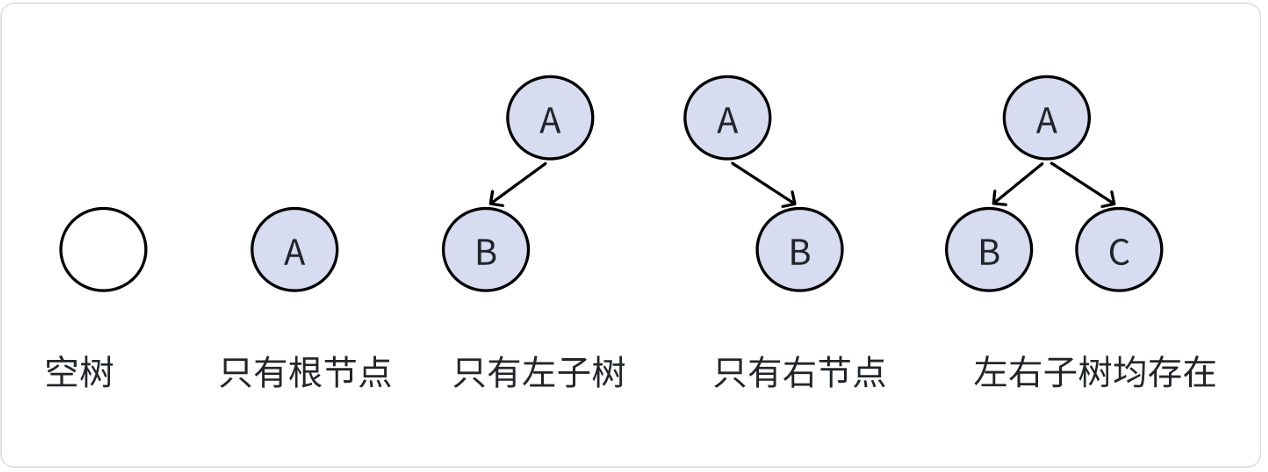
注意：對于任意的二叉樹都是由下列幾種情況復合而成

---

三、二叉樹的性質

在 二叉樹 中，葉子節點個數 == 分支節點個數 + 1

---

---

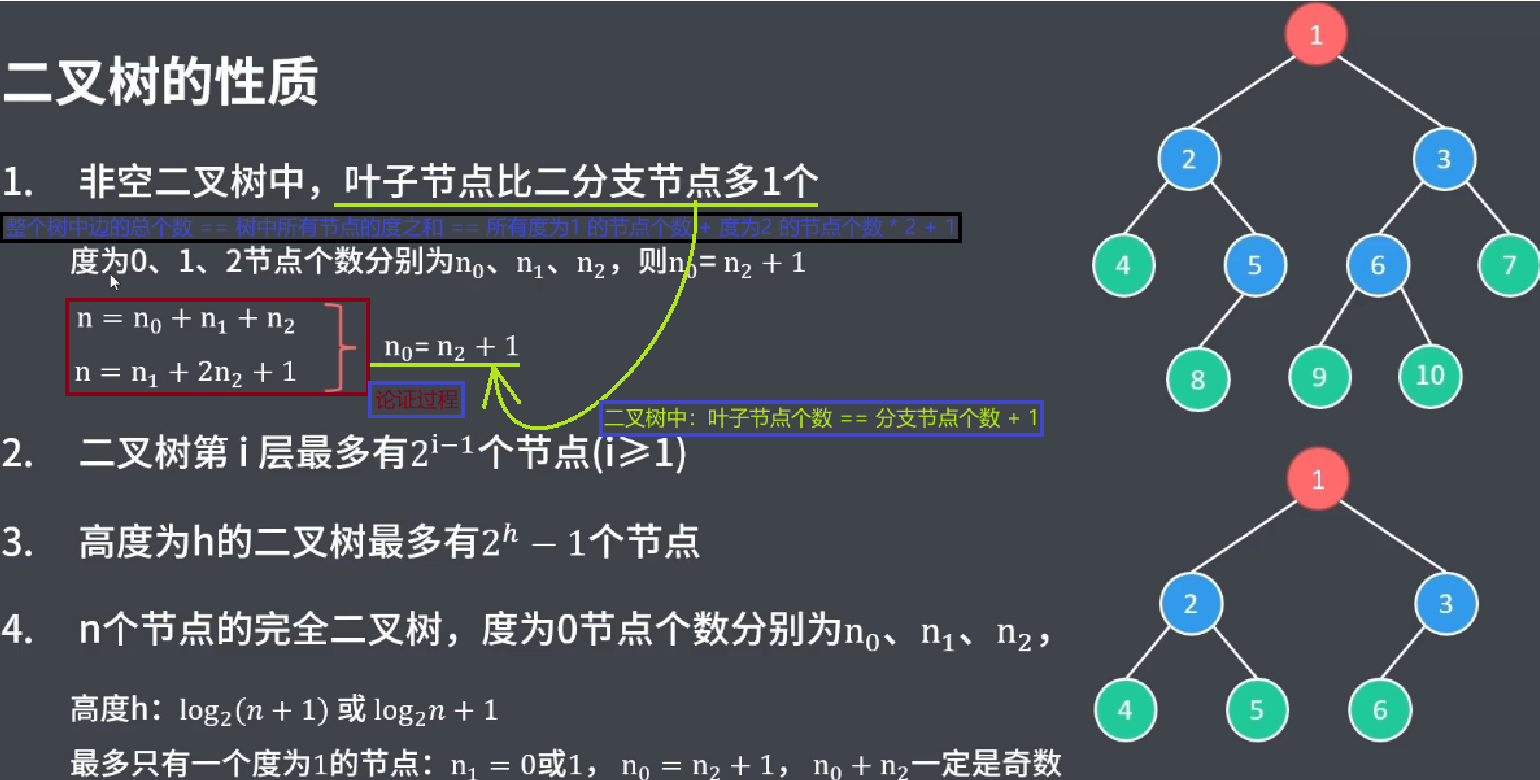
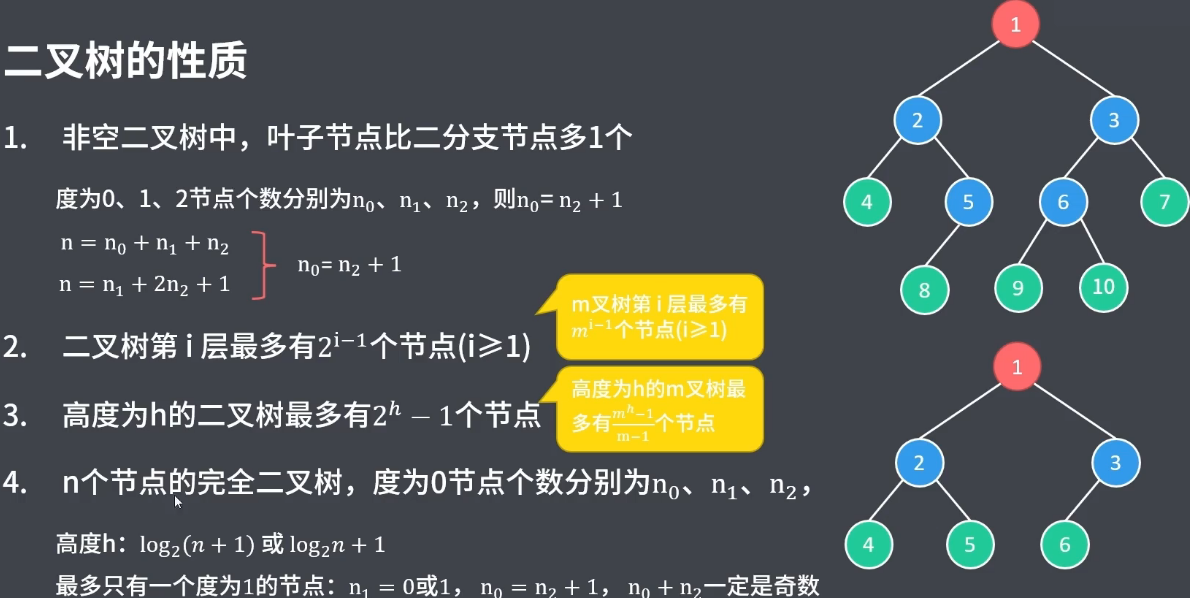
完全二叉樹中，最多只有一個度為1的節點： n₁ = 0 或 n₁ = 1；

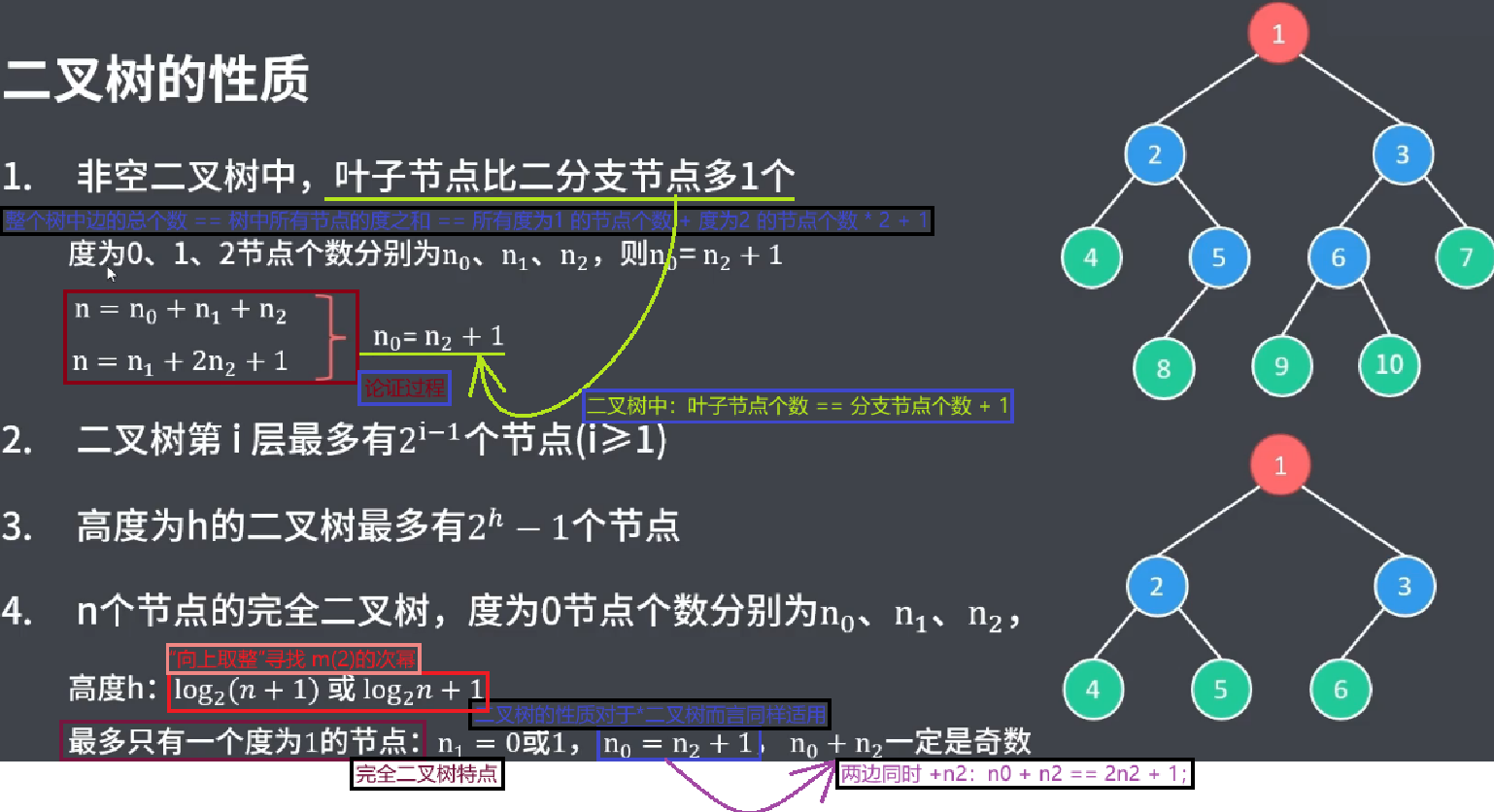
因此，給定節點個數 n，即可求得 n₀ n₁ n₂（因為 完全二叉樹特點：n₁為定值）

---

🌟 各位看官好，我是工藤新一1呀~

🌈 愿各位心中所想，終有所致！