前言

數據結構中的堆是一種結構，C語言的堆是空間管理的程序員malloc，free的空間，兩者沒多大關系。

1.堆

• 邏輯上

  堆（Heap）是一類基于完全二叉樹的特殊數據結構。通常將堆分為兩種類型：

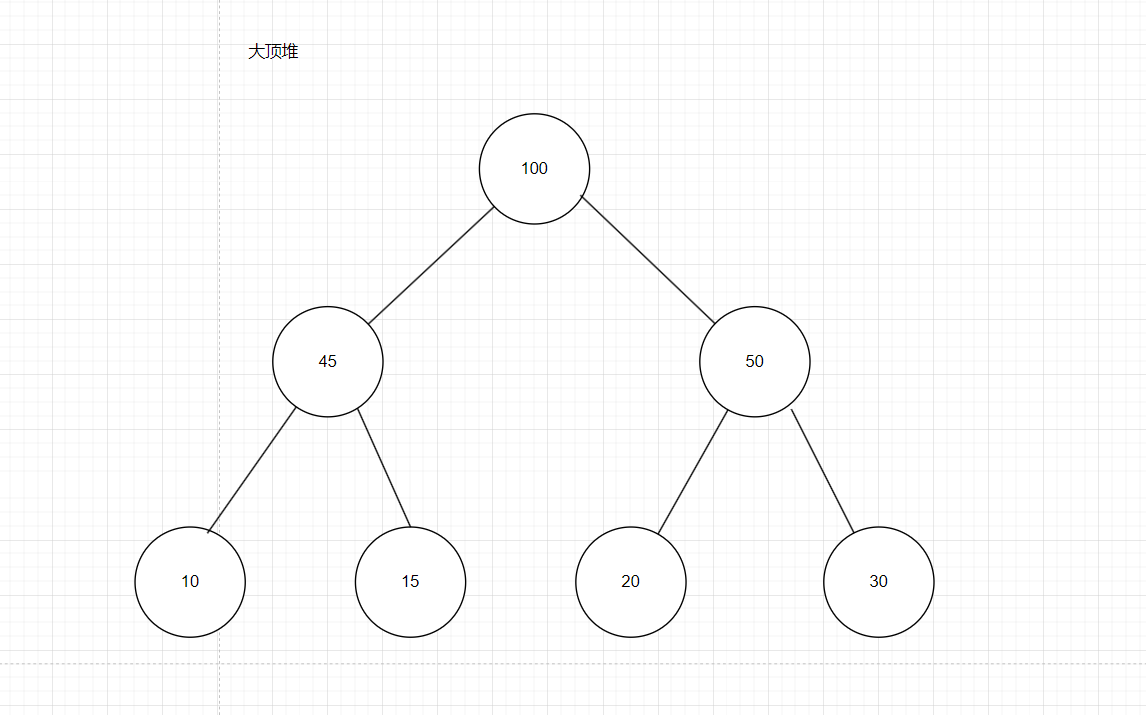
  1.大頂堆（Max Heap）：在大頂堆中，根結點的值必須大于他的孩子結點的值，對于二叉樹中所有子樹都滿足此規律
  

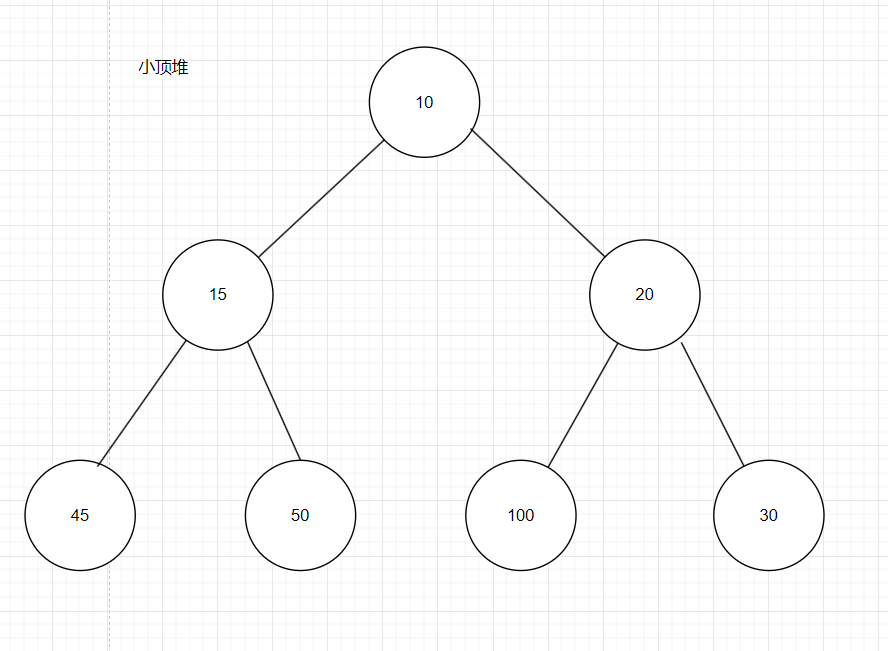
  2.小頂堆（Min Heap）：在小頂堆中，根結點的值必須小于他的孩子結點的值，對于二叉樹中所有子樹都滿足此規律
  

• 物理上

  之前有個性質：完全二叉樹中用數組空間來存儲結構，從1號下標開始存儲第一個元素，i號下標的根節點是2\i，左孩子2i,右孩子2i+1，接下來我們來看下怎么處理堆的邏輯。

2.堆的操作邏輯

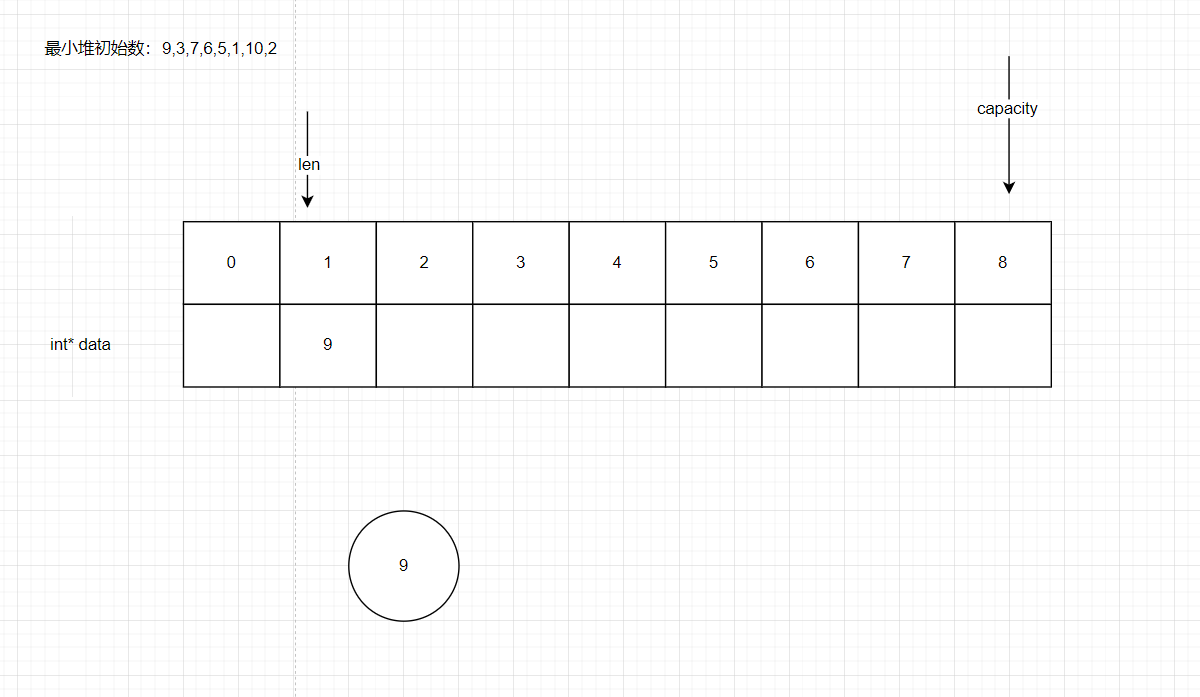
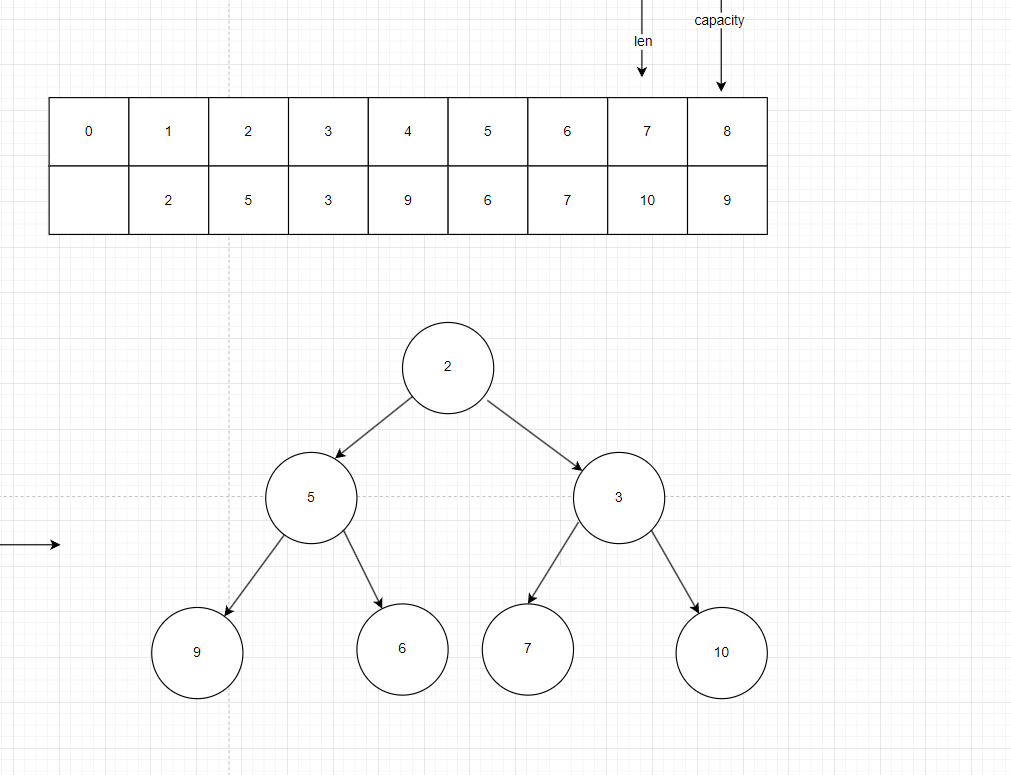
如圖，有8個數組組成了最小堆初始化數，我已經申請了9個空間（因為是完全二叉樹用數組空間存儲，從1號下標開始存元素），定義兩個 指針：len指針用來表示待插入位置，capacity用來表示數組空間容量

插入邏輯：

1.在最后一個位置上插入新元素，從代碼角度講 ++len;data[len]=v;
2.如果是小頂堆，找這個元素的父節點，如果父節點的值大于這個元素，交換兩個節點的值
3.繼續交換節點的父節點繼續執行條件判斷，是否交換
4.直到找到根或者已不滿足條件

2，3，4我們的稱為上浮操作

如圖初始化時把9放進來

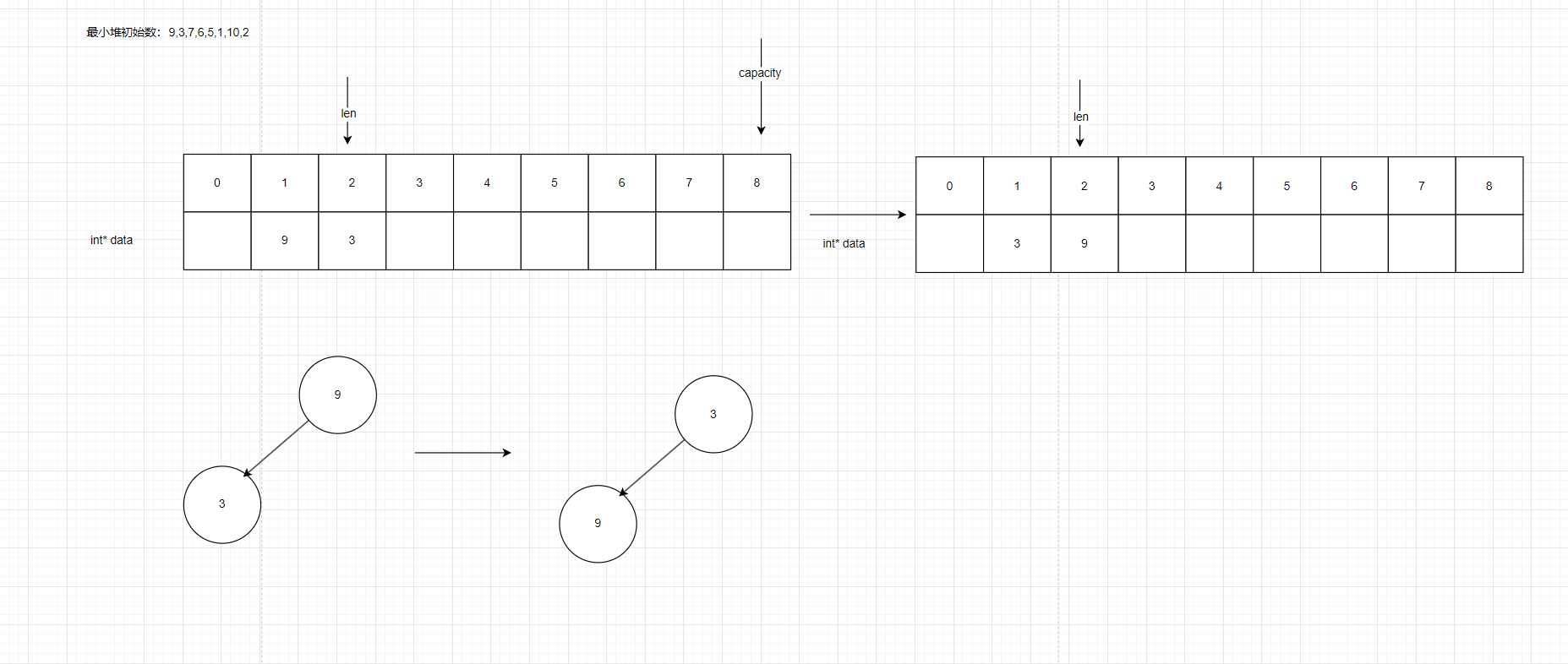
把3放進來，發現3比9小，于是交換兩個節點的值，并在數據區里也更新對應的值

把7放進來

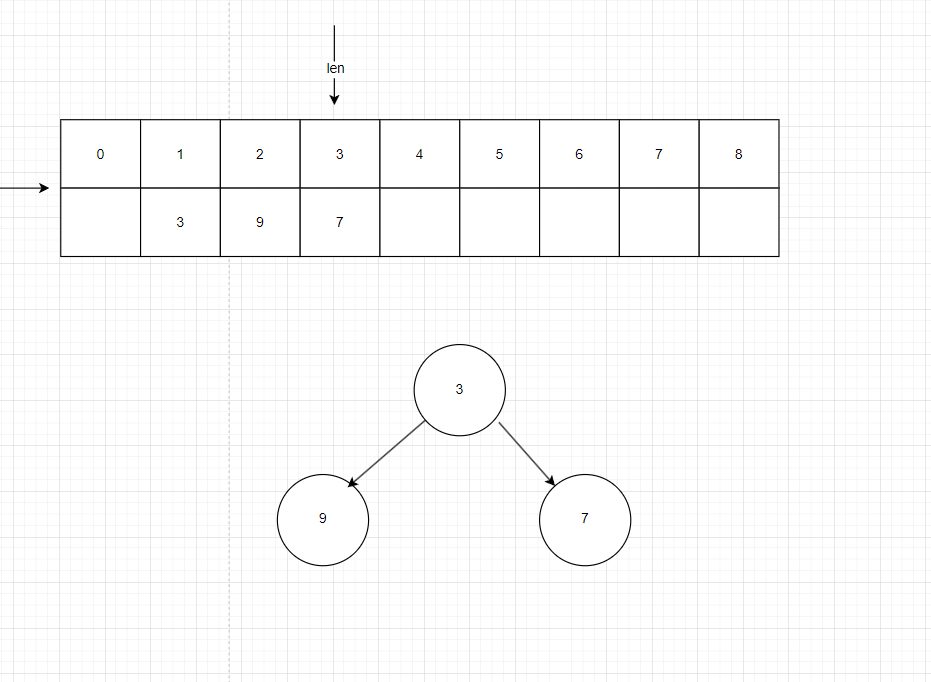
把6放進來，發現父節點9的值比它大，交換

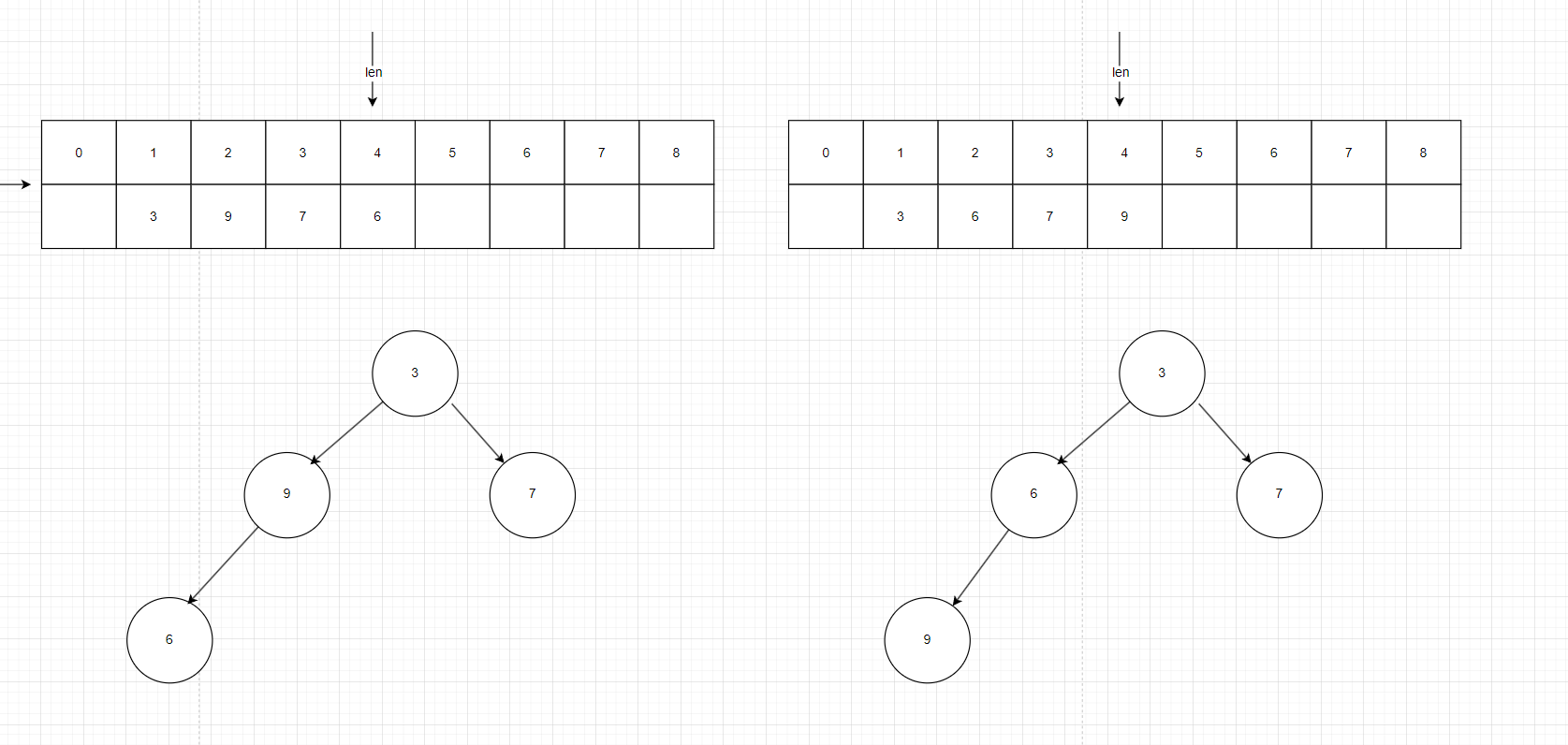
一直這樣直到把全部數字都放進堆中，最終結果如圖

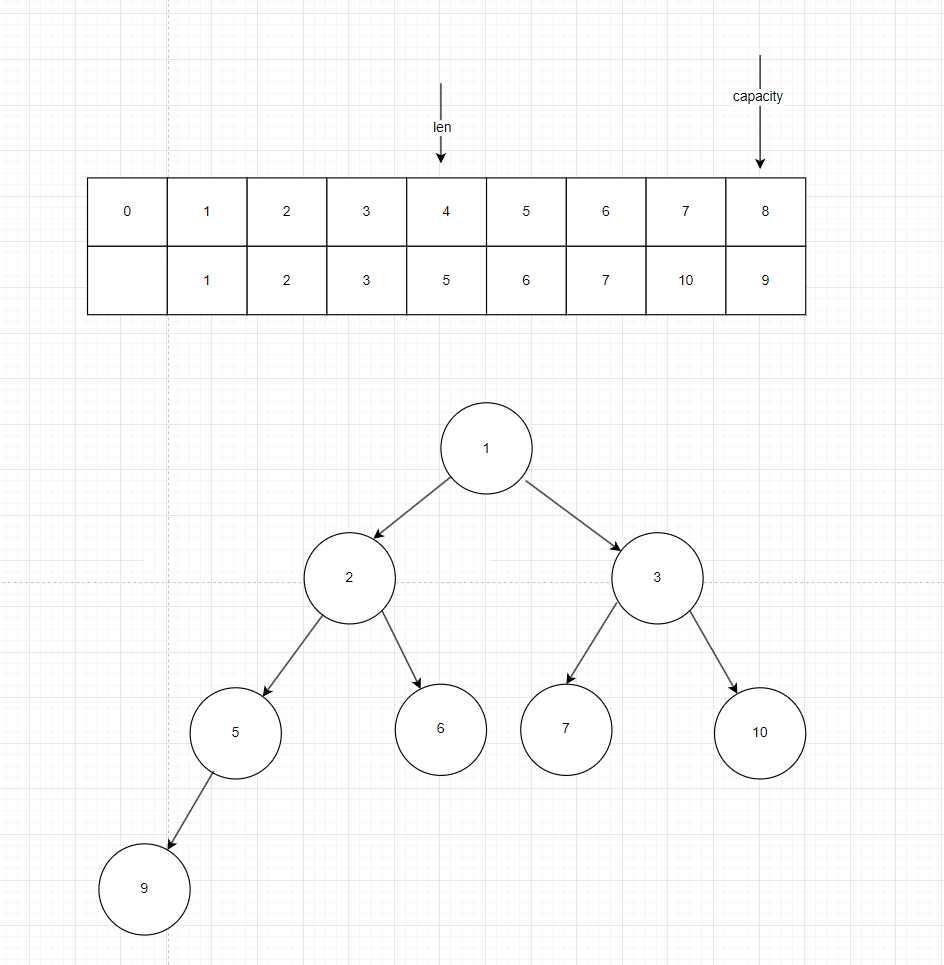
提取數據：
1.提取根元素，提取到最值
2.我們不能直接給它刪了，我們要繼續保持這顆樹的邏輯結構
3.把最后一個元素放到根節點的值，有效長度再減1，等價于刪除最后一個元素(因為刪除完全二叉樹的節點時都是刪除葉子節點，這樣才可以保持樹的結構，但是沒有滿足小頂堆的約束)。
4.把現在的根節點的值放入到正確的位置

3，4我們稱為下沉。

如圖我們要提取根節點1，按照上述邏輯，我們要保持整棵樹的結構，先把葉子節點9的值交給1，刪除葉子節點，len–

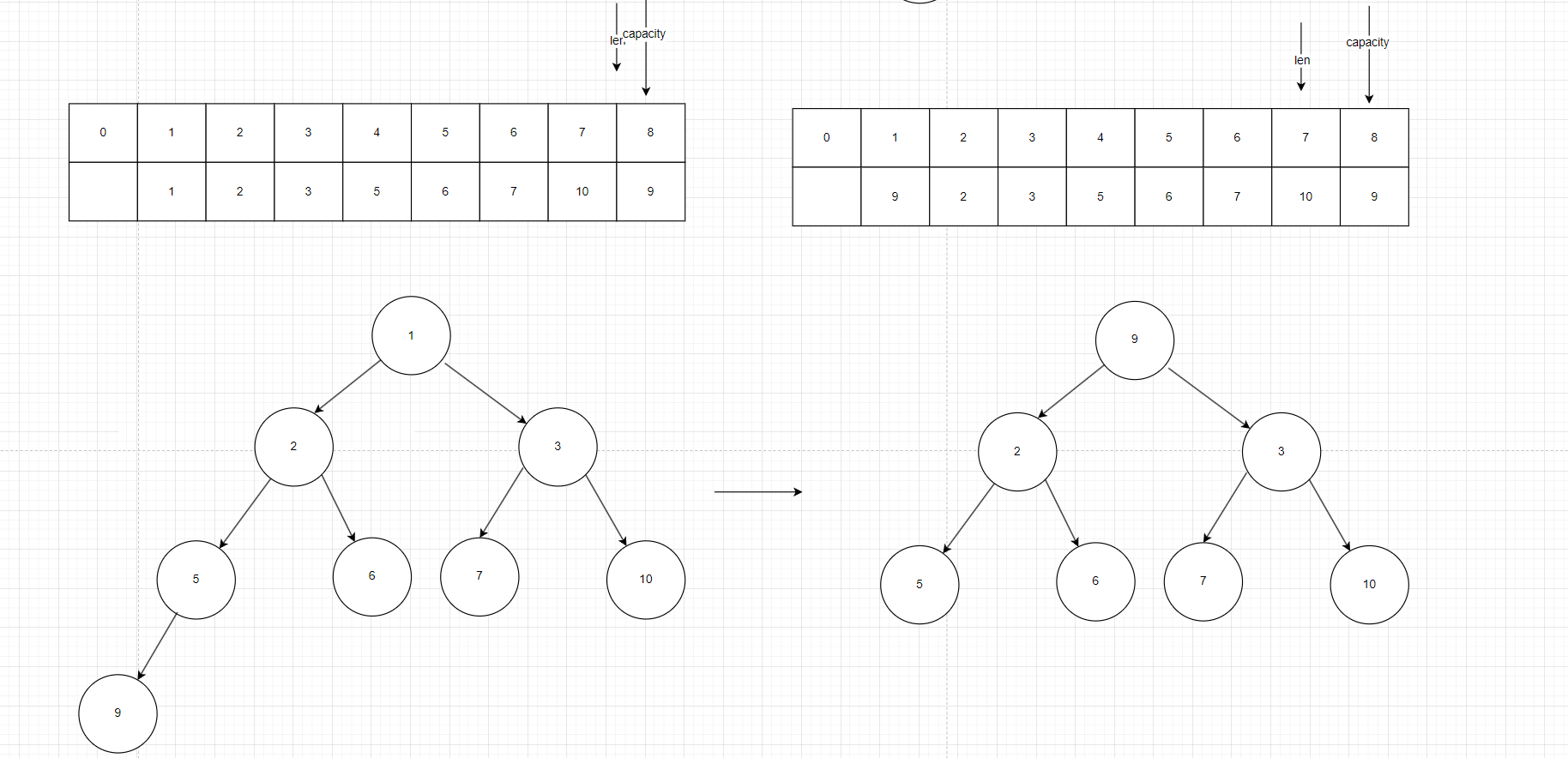
開始完成約束條件，把根節點的值放入正確的位置，此時我們需要比較根節點的左右孩子的大小，選擇較小的那個，因為如果我們把9和3交換位置，3比2大依然沒有滿足小頂堆的約束，所以9和2交換位置，此時9來到2的位置，再次比較左右孩子的大小，發現5是較小值，交換5和9。如圖：

如果我們有100個元素，但是我們只想要提取前5個，你可以把這100個排好序，然后取前5個即可，但是這樣時間復雜度是O(n²)，我們完全可以用小頂堆排好這100個元素，然后提取5次小頂堆的根節點，時間開銷就很少，這樣效率就較好。例如應用：Top10，在音樂榜單中的前10首歌曲，就可以采取這種思想，把成千上萬首歌放進小頂堆，然后取10次小頂堆的根節點就拍好序了。

3.堆的代碼實現

數據結構實現

#ifndef MINI_HEAP_H
#define MINI_HEAP_H
#include "../sortHelper.h"
// 定義小頂堆的結構
typedef struct {keyType *data;int len;            // 堆data的長度int capacity;       // 最大容量
} MiniHeap;MiniHeap *createMiniHeap(int n);            // 產生n個元素的堆空間
void releaseMiniHeap(MiniHeap *miniHeap);// 插入
void insertMiniHeap(MiniHeap *heap, keyType e);
// 提取
keyType extractMinMiniHeap(MiniHeap *heap);
#endif //MINI_HEAP_H

創建樹的接口：MiniHeap *createMiniHeap(int n);

MiniHeap * createMiniHeap(int n) {MiniHeap * heap = malloc(sizeof(MiniHeap));if (heap==NULL) {return NULL;}heap->data = malloc(sizeof(int)*n);if (heap->data == NULL) {free(heap);return NULL;}heap->capacity=n;heap->len=0;return heap;
}

釋放樹的接口：void releaseMiniHeap(MiniHeap *miniHeap);

void releaseMiniHeap(MiniHeap *miniHeap) {if (miniHeap) {if (miniHeap->data) {free(miniHeap->data);}free(miniHeap);}
}

插入接口：void insertMiniHeap(MiniHeap *heap, keyType e);

static void shiftUp(MiniHeap *miniHeap, int k) {keyType tmp;// k/2表示父節點，k節點子節點while (k > 1 && miniHeap->data[k / 2] > miniHeap->data[k]) {tmp = miniHeap->data[k];miniHeap->data[k] = miniHeap->data[k / 2];miniHeap->data[k / 2] = tmp;k /= 2;}
}void insertMiniHeap(MiniHeap *heap, keyType e) {//防越界if (heap->len + 1 > heap->capacity) {return;}heap->data[++heap->len] = e;shiftUp(heap,heap->len);
}

我這里寫了一個內在的接口shifUp即我在2.堆的操作邏輯中的2，3，4操作中的上浮操作，相信大家應該能看懂

提取接口:keyType extractMinMiniHeap(MiniHeap *heap)；

static void shiftDown(MiniHeap *miniHeap, int k) {keyType tmp;while (2 * k <= miniHeap->len) {        // 保證有左孩子int index = 2 * k;if (index + 1 <= miniHeap->len && miniHeap->data[index + 1] < miniHeap->data[index]) {++index;}if (miniHeap->data[k] <= miniHeap->data[index]) {break;}tmp = miniHeap->data[k];miniHeap->data[k] = miniHeap->data[index];miniHeap->data[index] = tmp;k = index;}
}keyType extractMinMiniHeap(MiniHeap *heap) {//防越界if (heap->len <= 0) {return 0;}keyType ret=heap->data[1];heap->data[1]=heap->data[heap->len--];shiftDown(heap,1);return ret;
}

注意在static void shiftDown(MiniHeap *miniHeap, int k)我們不僅要檢驗左子樹有沒有越界還要檢驗右子樹有沒有越界，先保證有左孩子，如果我們的右孩子沒有越界并且右孩子的值小于左孩子的值，那就拿到右孩子的索引，如果父節點的值已經小于了左右孩子節點中的較小值就直接退出，然后進行交換值。

來測一下：

#include <stdio.h>
#include "miniHeap.h"void test01() {int data[] = {9, 3, 7, 6, 5, 1, 10, 2};int n = 20;MiniHeap *miniHeap = createMiniHeap(n);for (int i = 0; i < sizeof(data) / sizeof(data[0]); i++) {insertMiniHeap(miniHeap, data[i]);}printf("extra: ");for (int i = 0; i < sizeof(data) / sizeof(data[0]); i++) {printf("%d ", extractMinMiniHeap(miniHeap));}printf("\n");releaseMiniHeap(miniHeap);
}int main() {test01();return 0;
}

結果：

D:\work\DataStruct\cmake-build-debug\04_Sort\HeapSort.exe
extra: 1 2 3 5 6 7 9 10進程已結束，退出代碼為 0

我們再寫一個接口來測試堆排序的時間復雜度：

#include "heapSort.h"void miniHeapSort(SortTable *table) {MiniHeap *heap = createMiniHeap(table->length);for (int i = 0; i < table->length; i++) {insertMiniHeap(heap, table->data[i].key);}for (int i = 0; i < table->length; i++) {table->data[i].key = extractMinMiniHeap(heap);}releaseMiniHeap(heap);
}

用快速排序來進行對比：

#include <stdio.h>
#include "miniHeap.h"
#include "heapSort.h"
#include "../02_SwapSort/quickSort.h"void test01() {int data[] = {9, 3, 7, 6, 5, 1, 10, 2};int n = 20;MiniHeap *miniHeap = createMiniHeap(n);for (int i = 0; i < sizeof(data) / sizeof(data[0]); i++) {insertMiniHeap(miniHeap, data[i]);}printf("extra: ");for (int i = 0; i < sizeof(data) / sizeof(data[0]); i++) {printf("%d ", extractMinMiniHeap(miniHeap));}printf("\n");releaseMiniHeap(miniHeap);
}void test02() {int n = 100000;SortTable *table1 = generateRandomArray(n, 0, n + 5000);SortTable *table2 = copySortTable(table1);testSort("Heap Sort", miniHeapSort, table1);testSort("quick Sort", quickSortV1, table2);releaseSortTable(table1);releaseSortTable(table2);
}int main() {test02();return 0;
}

結果：

D:\work\DataStruct\cmake-build-debug\04_Sort\HeapSort.exe
Heap Sort cost time: 0.013000s.
quick Sort cost time: 0.009000s.進程已結束，退出代碼為 0

可以看到兩者的排序時間是差不多的，這是因為堆排序和樹的高度有關，所以時間復雜度也是O(nlogn)。

大概先寫這些吧，今天的博客就先寫到這，謝謝您的觀看。