🔥個人主頁:胡蘿卜3.0
🎬作者簡介:C++研發方向學習者
📖個人專欄:??《C語言》《數據結構》?《C++干貨分享》
??人生格言:不試試怎么知道自己行不行

正片開始之前,我們來了解一下我們即將要來介紹、學習的這個數據結構——二叉樹。
二叉樹的作用:
(1)快速查找
二叉樹(尤其是二叉排序樹)可以用于高效的數據查找,其查找的時間復雜度為 O(log?n),最壞情況下為O(n)。這種特性使得二叉樹特別適合需要頻繁查找、插入和刪除操作的場景。(2)動態數據管理
由于二叉樹支持動態查詢,并且可以通過調整樹的結構來優化性能(例如 AVL 樹、紅黑樹),它被廣泛應用于需要動態管理數據的場景,如數據庫索引和內存管理。(3)有序序列生成
中序遍歷一棵二叉排序樹可以得到一個關鍵字的有序序列,這使得二叉樹成為一種有效的排序工具。構造二叉排序樹的過程本質上就是對無序序列進行排序的過程。(4)樹狀結構表示
許多現實世界的問題可以用樹狀結構來建模,例如網站目錄結構、文件系統等。雖然這些結構可能不是嚴格的二叉樹,但通過適當的轉換,它們可以使用二叉樹的相關算法來處理。
應用場景:
(1)網頁爬蟲中的遍歷
在互聯網工程中,當需要下載某個網站的所有網頁時,可以利用二叉樹的遍歷算法來模擬這一過程。這種算法能夠確保所有頁面都被訪問到,并且按照一定的順序進行處理。(2)二叉樹的展開
在某些特定的應用中,比如將二叉樹轉換為鏈表形式,可以通過遞歸的方式實現。例如,在先序遍歷的順序下,左子樹會被移到右指針位置,而左子樹的最后一個節點會指向原來的右子樹。(3)平衡二叉樹的應用
平衡二叉樹(如 AVL 樹、紅黑樹)通過保持樹的高度平衡來確保查找、插入和刪除操作的時間復雜度始終為O(logn)。這類樹結構廣泛應用于需要高性能數據檢索的場景,例如數據庫索引和操作系統調度器。(4)表達式樹
表達式樹是一種特殊的二叉樹,其中葉子節點表示操作數,內部節點表示運算符。這種結構可以用于解析和求值數學表達式,并且在編譯器設計中具有重要應用。(5)哈夫曼編碼
哈夫曼樹是一種帶權路徑長度最短的二叉樹,常用于數據壓縮領域。通過構建哈夫曼樹,可以生成最優前綴編碼,從而減少存儲空間或傳輸成本。(6)決策樹
在機器學習和人工智能領域,二叉樹可以用來表示決策過程。每個節點代表一個特征判斷,每個分支代表一個可能的結果,最終的葉子節點則代表最終的決策結果。
二叉樹這個部分學起來不會容易,但是會讓你覺得很有收獲,你慢慢會覺得學二叉樹很爽!
目錄
正文?
一、樹
1.1 樹的概念與結構
1.2 非樹形結構
1.3 樹的相關術語
1.4 樹的表示方法--孩子兄弟表示法
1.5 屬性結構實際運用場景
二、二叉樹
2.1 二叉樹的概念與結構
2.2 特殊的二叉樹
2.2.1 滿二叉樹
2.2.2 完全二叉樹
三、二叉樹的存儲結構
3.1 順序結構
3.2 鏈式結構
正文?
一、樹
樹是什么?數據結構中的樹和自然界中的樹有什么聯系嗎?有。


樹的根在地下,故曰“向陽而生”;樹形結構的根在上面——
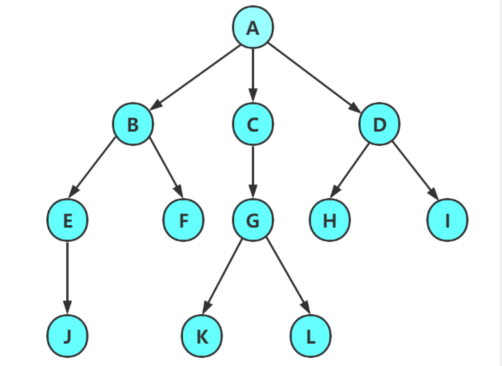
1.1 樹的概念與結構
樹是一種非線性的數據結構,它是由n(n>=0)個有限結點組成一個具有層次結構的集合。我們把它叫做樹是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。
- 有一個特殊的結點,稱為根節點,根節點沒有前驅結點。(根節點稱為父節點/雙親結點)
- 除根節點外,其余結點被分成M(M>0)個互不相交的集合(T1、T2、……、Tm),其中每一個集合Ti(1<=i<=m)又是一棵結構與樹類似的子樹。每棵樹的根節點有且只有一個前驅,可以有0個或者多個后繼。因此,樹是遞歸定義的。
1.2 非樹形結構
在樹形結構中,子樹之間不能有交集,否則就不是樹形結構!!!如果子樹之間有交集,那就是非樹形結構
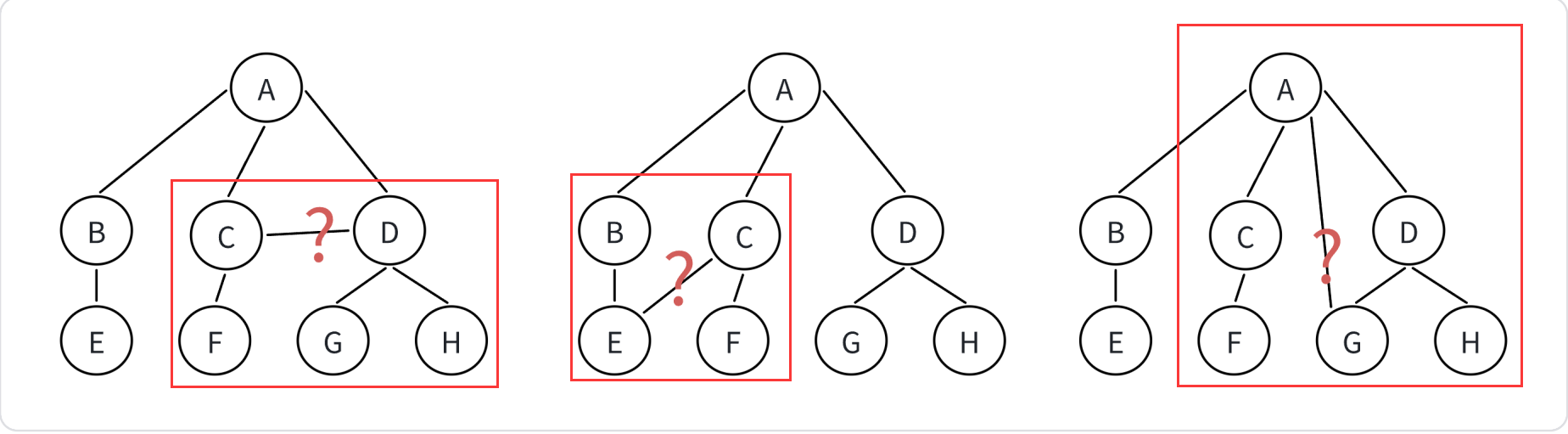
上圖中的三個都是非樹形結構,紅方框內的子樹有交集
注意:
- 子樹是不相交的(如果存在相交就是圖了,圖以后得課程會有講解)
- 除了根結點外,每個結點有且僅有一個父節點
- ?棵N個結點的樹有N-1條邊(記憶方式:2個結點有一條邊)
1.3 樹的相關術語
下圖就是一個樹形結構——
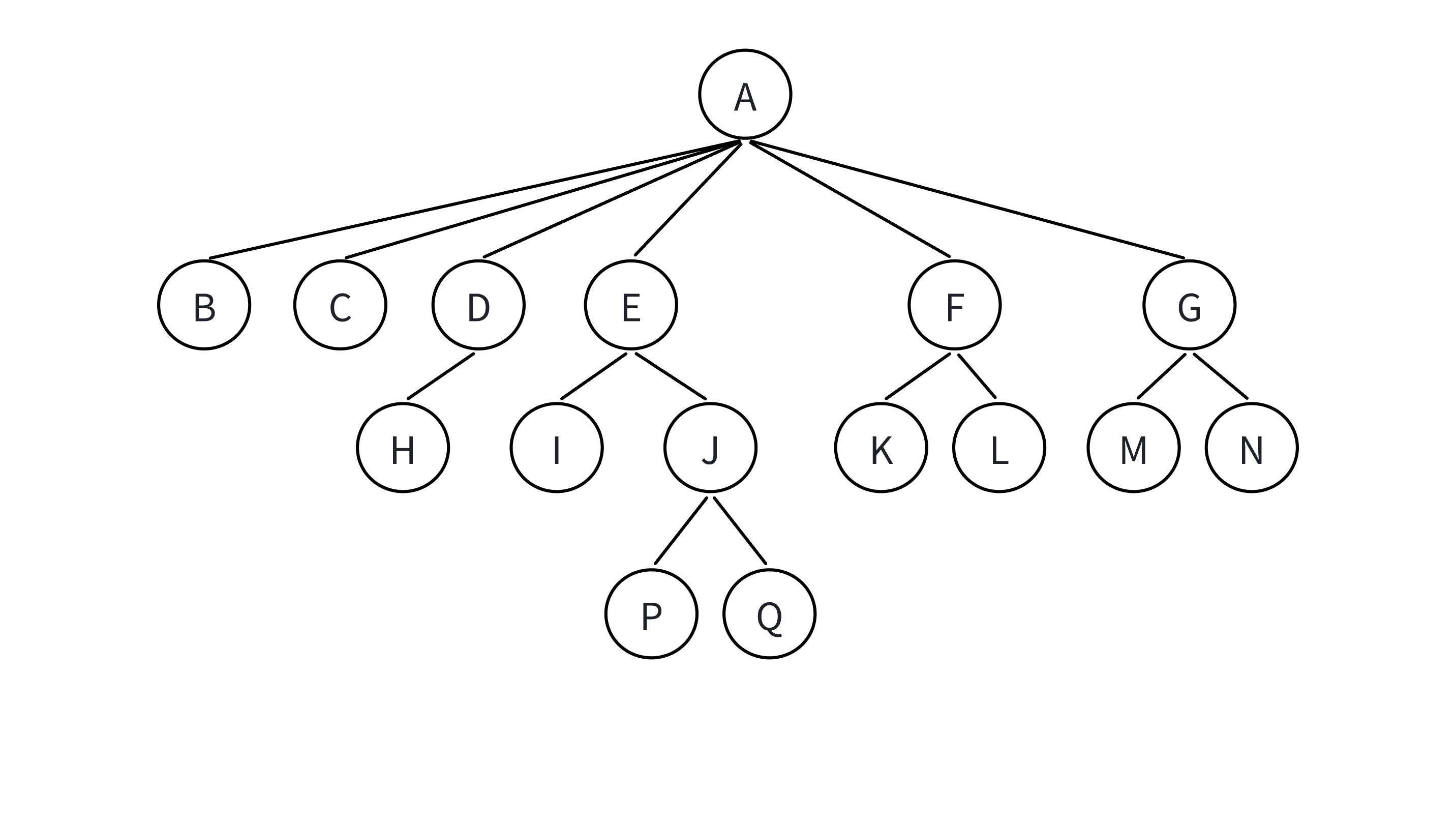
父結點/雙親結點:若一個結點含有子結點,則這個結點稱為其子結點的父結點,如上圖:A是B的父結點。
子結點/孩子結點:一個結點含有的子樹的根結點稱為該結點的子結點,如上圖:B是A的孩子結點。
結點的度:一個結點有幾個孩子,他的度就是多少,比如A的度為6,F的度為2,K的度為0。
樹的度:一棵樹中,最大的結點的度稱為樹的度,如上圖:樹的度為6。
葉子結點/終端結點:度為0的結點稱為葉結點,如上圖: B、C、H、I . . .等結點為葉結點。
分支結點/非終端結點:度不為0的結點,如上圖: D、E、F、G... 等結點為分支結點。
兄弟結點:具有相同父結點的結點互稱為兄弟結點(必須是親兄弟),如上圖: B、C 是兄弟結點。
結點的層次:從根開始定義起,根為第 1 層,根的子結點為第 2 層,以此類推。
樹的高度或深度:樹中結點的最大層次,如上圖:樹的高度為4。
結點的祖先:從根到該結點所經分支上的所有結點,如上圖: A 是所有結點的祖先。
路徑:一條從樹中任意節點出發,沿父結點 - 子節點連接,達到任意節點的序列,比如A到Q的路徑為: A-E-J-Q、H到Q的路徑H-D-A-E-J-Q。
子孫:以某結點為根的子樹中任一結點都稱為該結點的子孫,如上圖:所有結點都是A的子孫。
森林:由m(m>0)棵互不相交的樹的集合稱為森林。
?
1.4 樹的表示方法--孩子兄弟表示法
樹結構相對線性表就比較復雜了,要存儲表示起來就比較麻煩了,既要保存值域,也要保存結點和結點之間的關系,實際中樹有很多種表示方式如:雙親表示法,孩子表示法、孩子雙親表示法以及孩子兄弟表示法等。我們這里就簡單的了解其中最常用的孩子兄弟表示法:
struct TreeNode
{struct Node* child; // 左邊開始的第?個孩?結點struct Node* brother; // 指向其右邊的下?個兄弟結點int data; // 結點中的數據域
}比如說下面這幅圖中的樹結構:
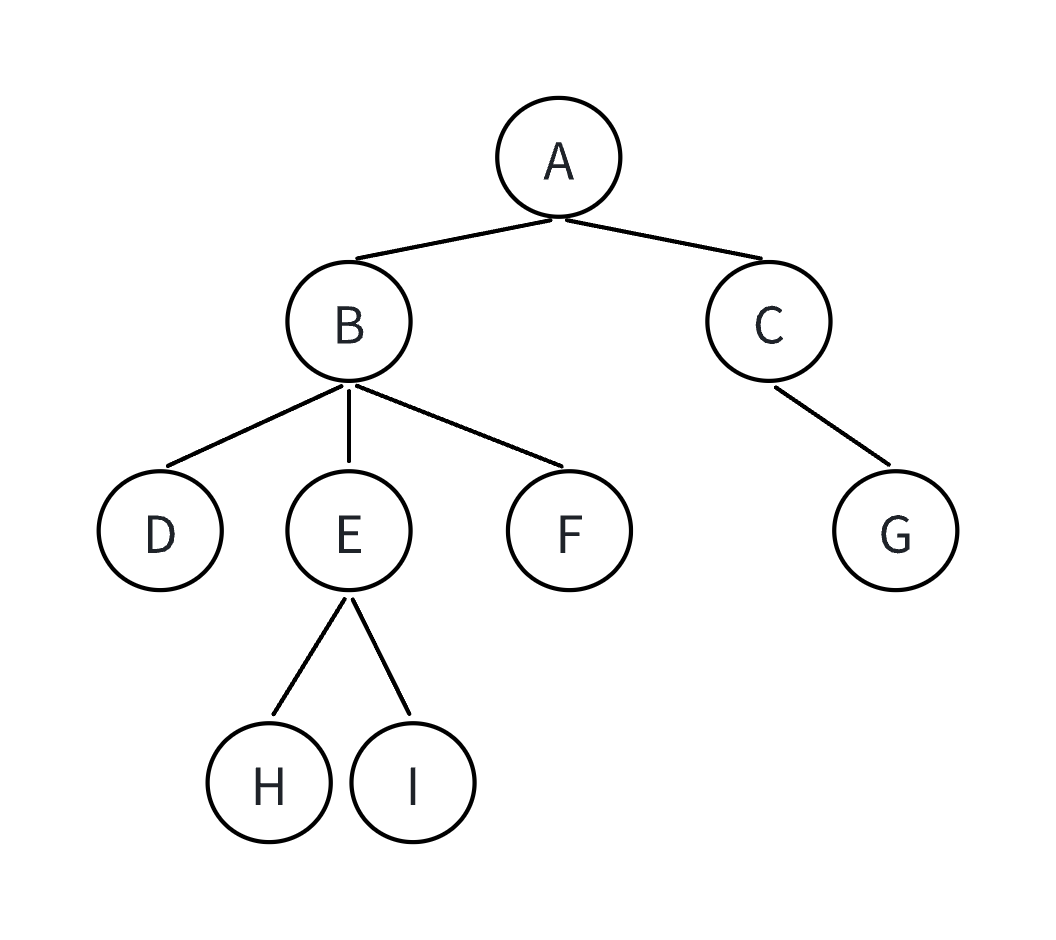
我們用孩子兄弟表示法可以這樣表示——
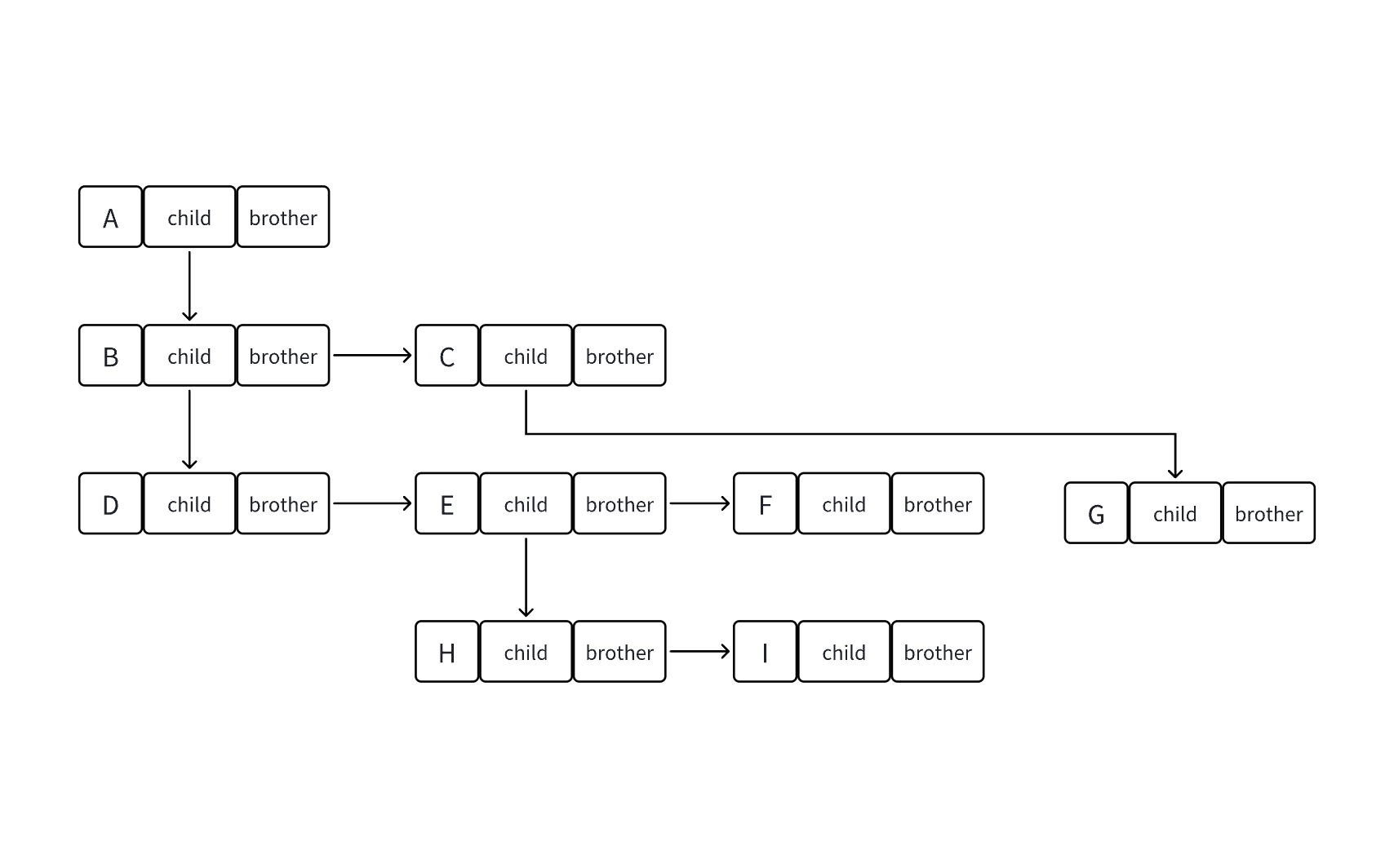
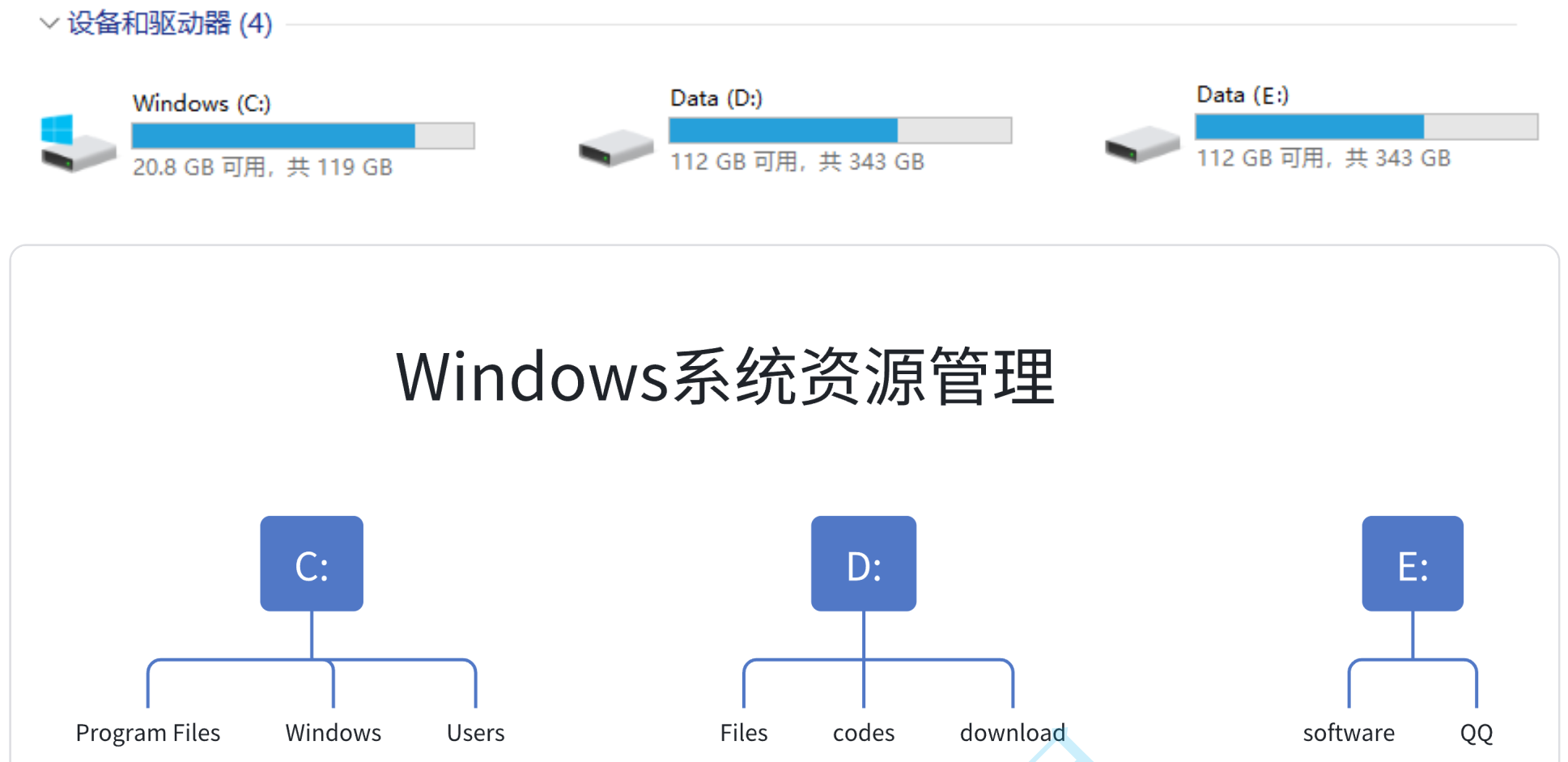
1.5 屬性結構實際運用場景
文件系統是計算機存儲和管理文件的一種方式,它利用樹形結構來組織和管理文件和文件夾。在文件系統中,樹結構被廣泛應用,它通過父結點和子結點之間的關系來表示不停層級的文件和文件夾之間的關聯。
二、二叉樹
2.1 二叉樹的概念與結構
在樹形結構中,我們最常用的就是二叉樹,一棵二叉樹是結點的一個有限集合,該集合由一個根節點加上兩棵分別稱為左子樹和右子樹的二叉樹組成或者二叉樹為空。
結構:
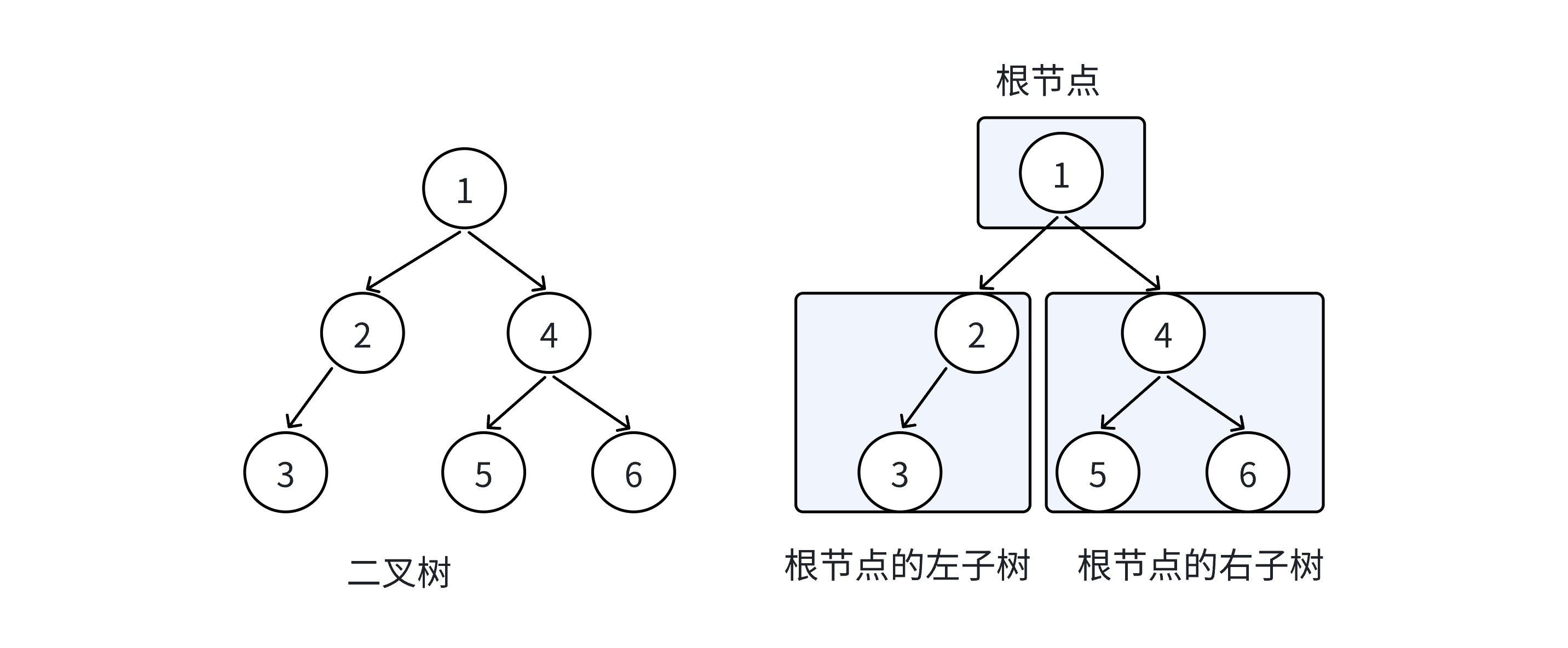
從上圖可以看出:
- 二叉樹不存在度大于2的結點(0,1,2)
- 二叉樹的子樹有左右之分,次序不能顛倒,因此二叉樹是有序樹
注意:對于任意的?叉樹都是由以下幾種情況復合而成的:
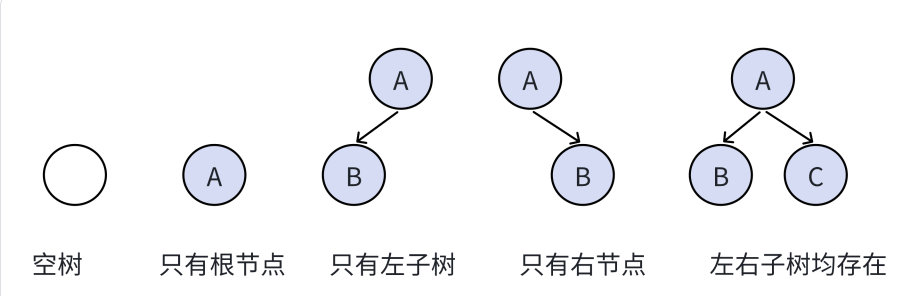
因此二叉樹不是很好駕馭,于是我們定義了特殊的二叉樹,比如滿二叉樹、完全二叉樹等。
2.2 特殊的二叉樹
樹->二叉樹->特殊的二叉樹->滿二叉樹
2.2.1 滿二叉樹
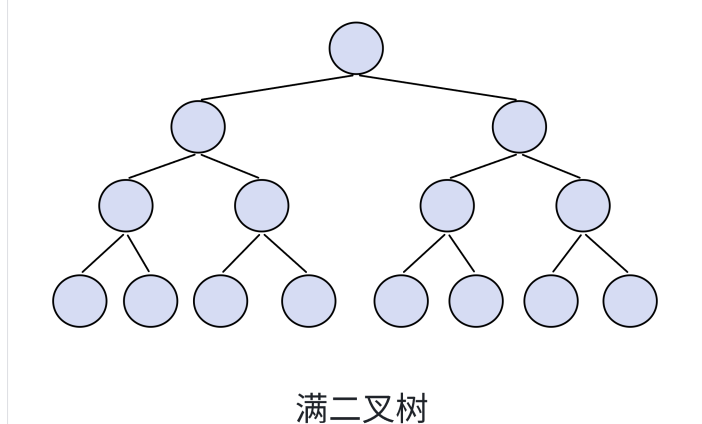
滿二叉樹(度為2,即最大結點個數為2),每一層結點數都最大,層數為K,結點總數為2^(k-1),這就是滿二叉樹。
滿二叉樹的結點總數是怎么求出來的呢?
2.2.2 完全二叉樹
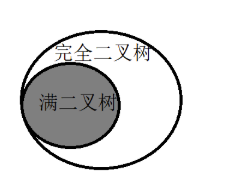
完全二叉樹是效率很高的數據結構,完全二叉樹是由滿二叉樹而引出來的。
簡單來說
完全二叉樹就是:除了最后一層,其他每層結點個數都達到最大,最后一層結點個數不一定達到最大,滿二叉樹就是完全二叉樹的一種,并且完全二叉樹的結點從左向右依次排列。
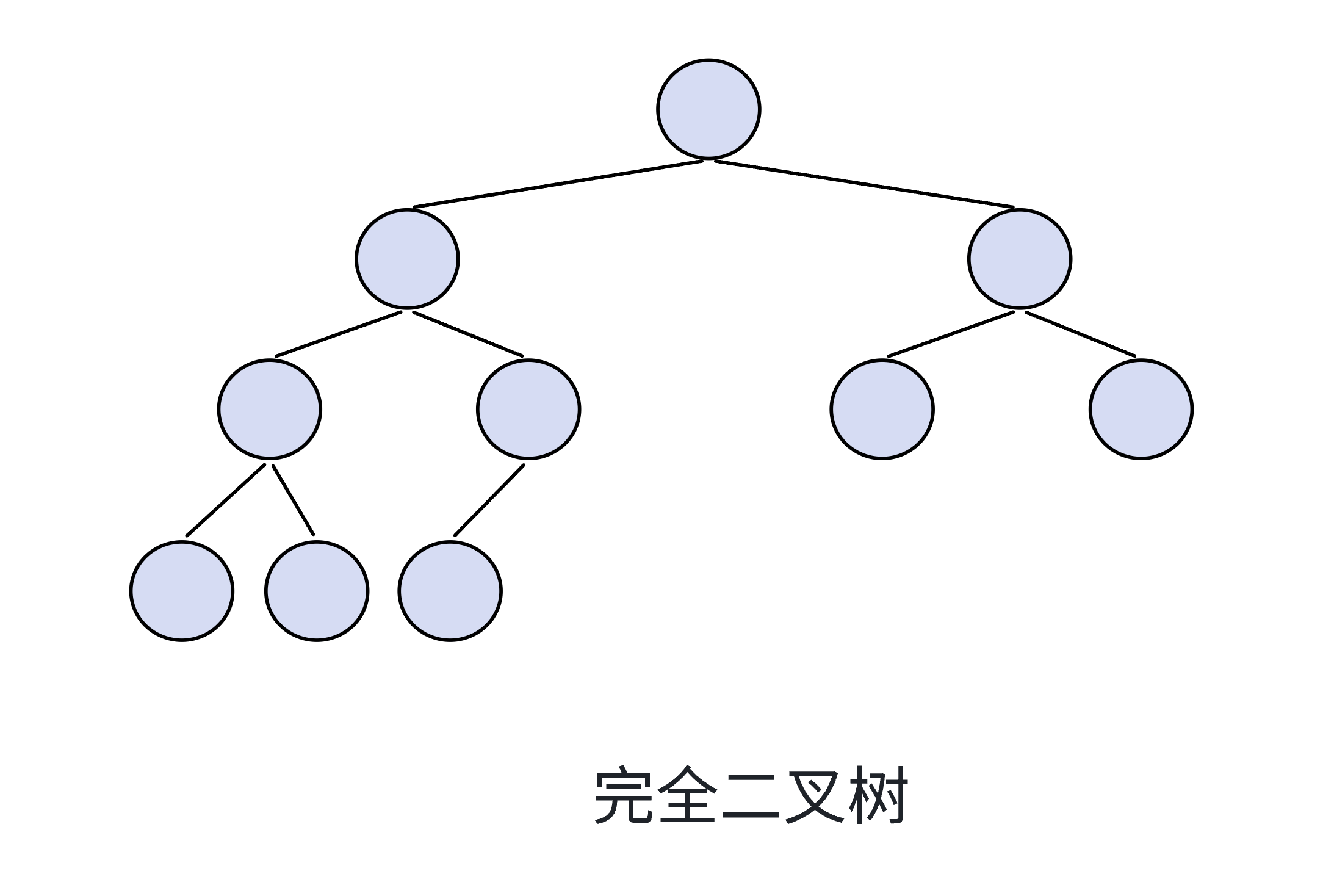
完全二叉樹就是:除了最后一層,其他每層結點個數都達到最大,最后一層結點個數不一定達到最大,滿二叉樹就是完全二叉樹的一種,并且完全二叉樹的結點從左向右依次排列。
完全二叉樹的每層結點的個數達到最大就是滿二叉樹;除了最后一層,其他每層結點個數都達到最大就是完全二叉樹
完全二叉樹的結點是從左往右依次排列的——
這是非常重要的一個知識點,觀察下圖,是不是一個完全二叉樹——
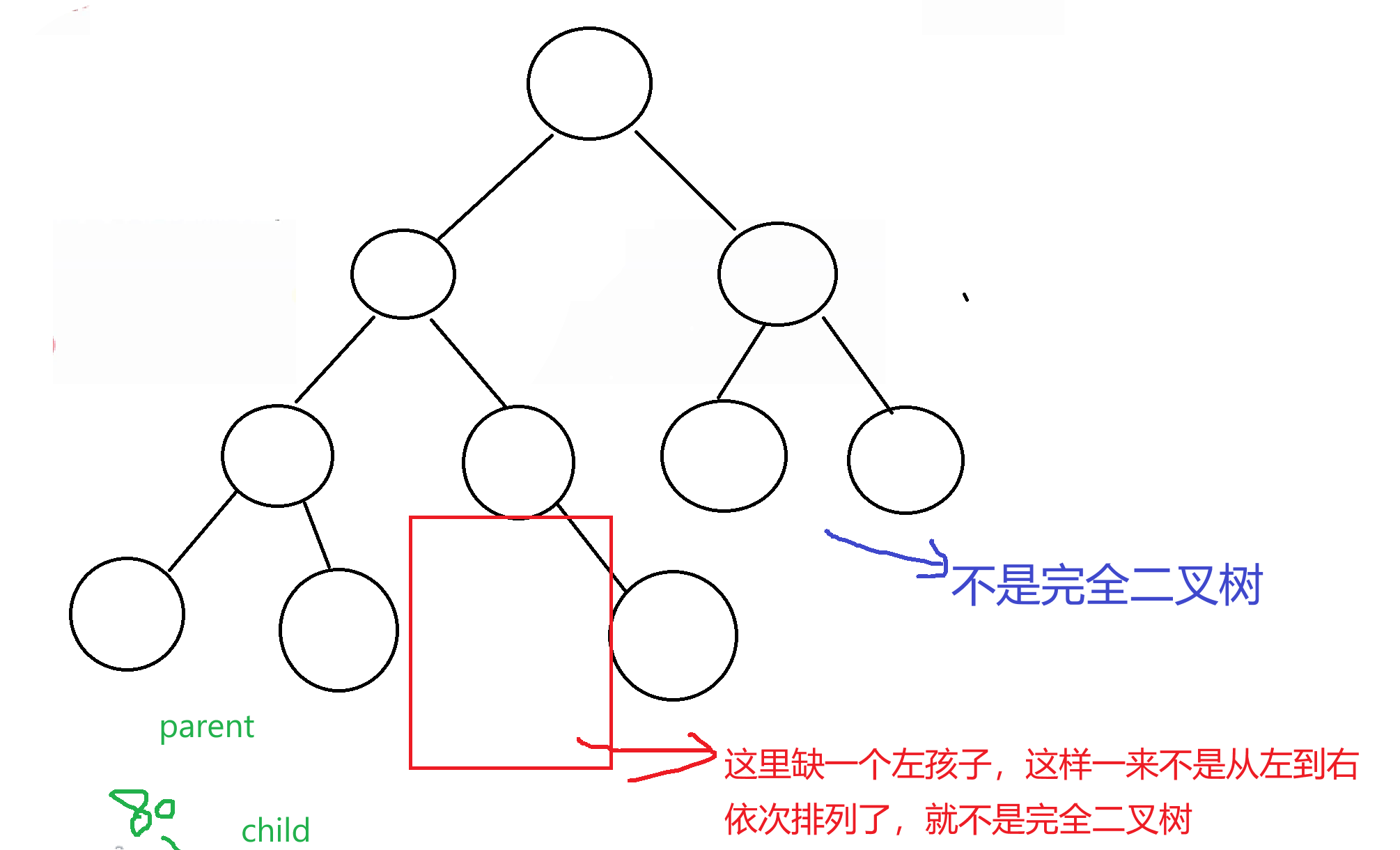
缺一個左孩子,這樣一來不是從左到右依次排列了,就不是完全二叉樹
二叉樹的性質:

三、二叉樹的存儲結構
二叉樹一般可以使用二中存儲結構,一種順序結構,一種鏈式結構
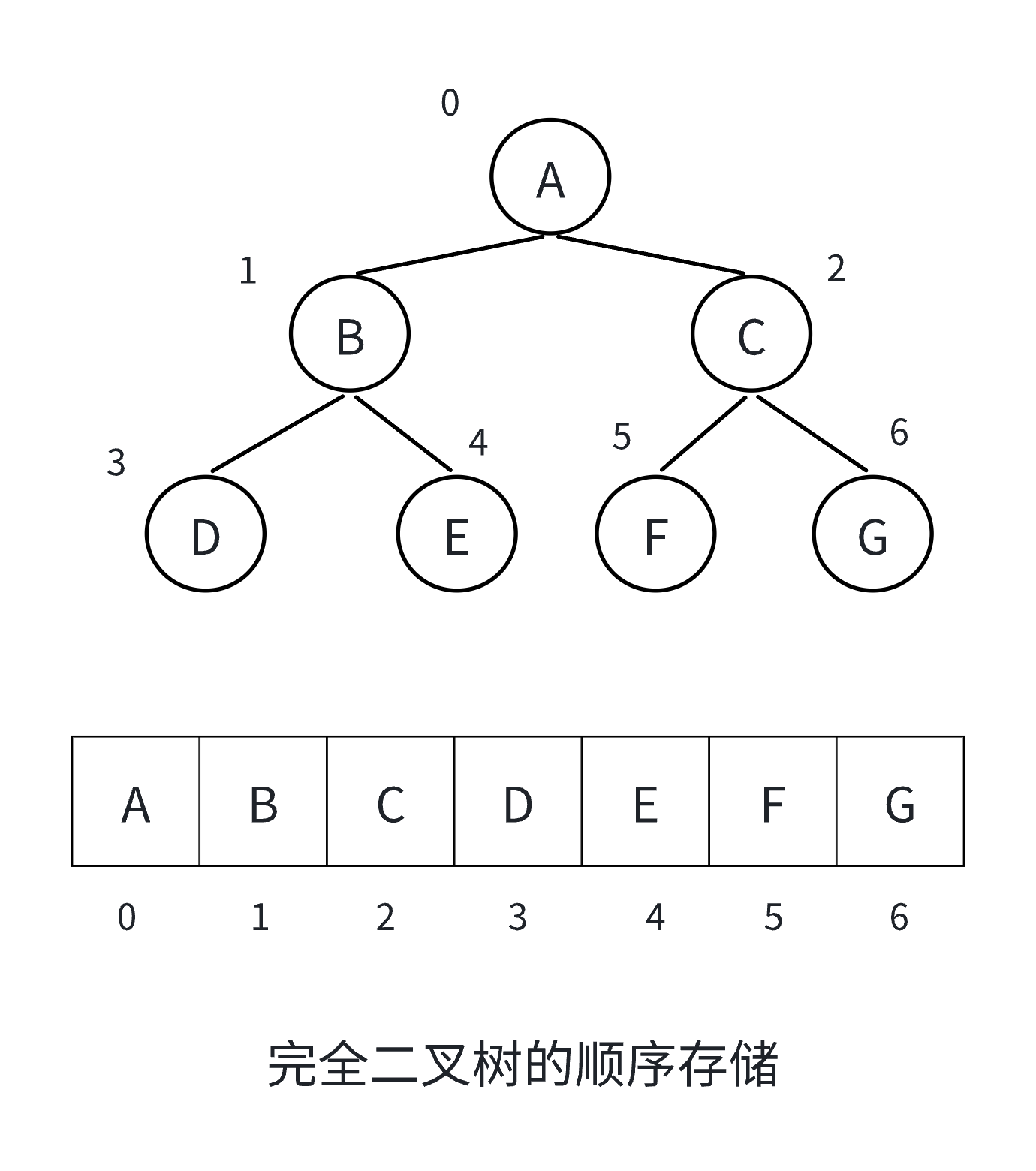
3.1 順序結構
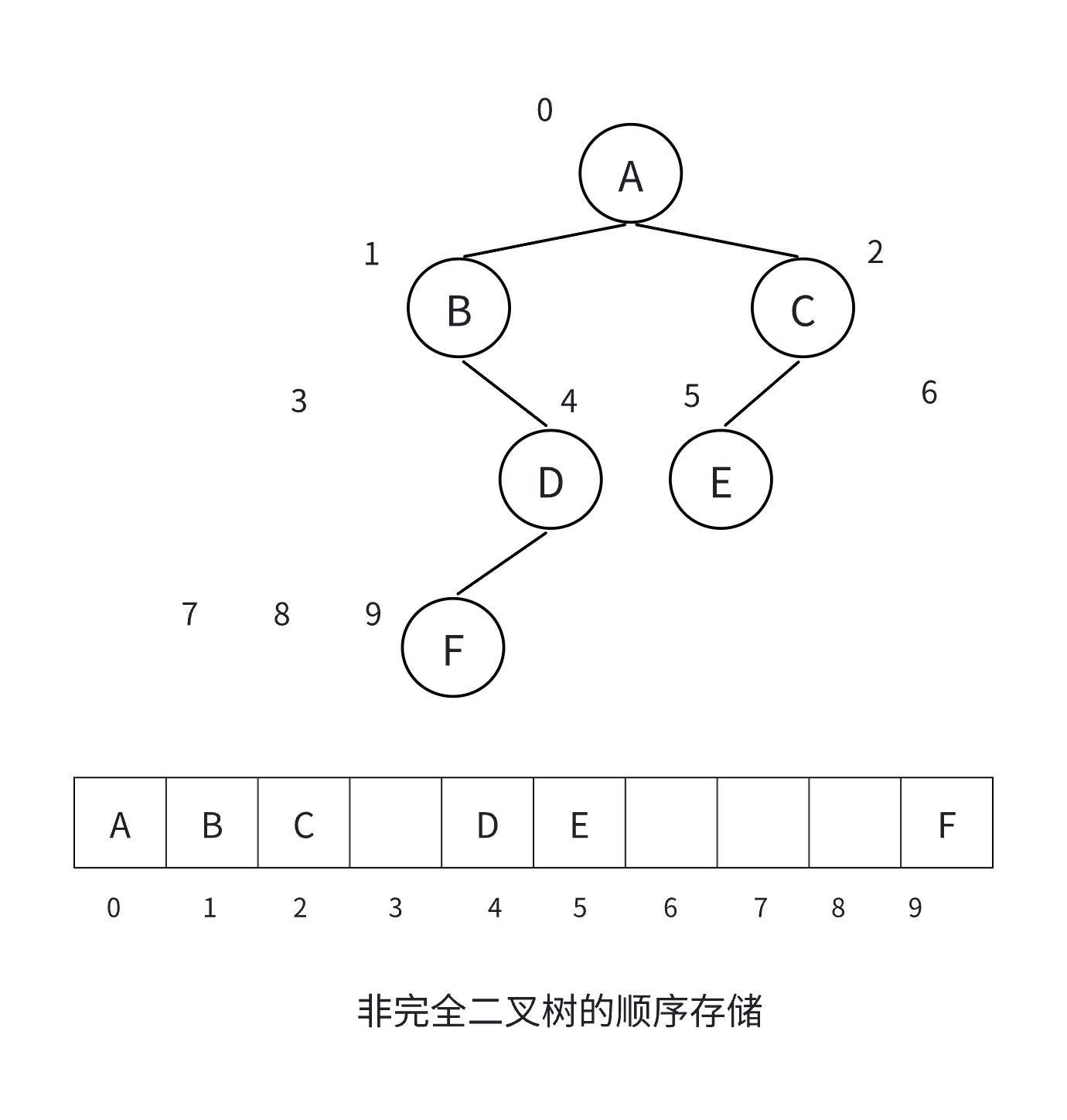
順序結構存儲就是使用數組來存儲,一般使用數組只適合表示完全二叉樹,因為不是完全二叉樹會有空間的浪費,完全二叉樹更適合使用順序結構存儲。
我們通常把堆(一種二叉樹)使用順序結構的數組來存儲,需要注意的是這里的堆和操作系統虛擬進程地址空間中的堆是兩回事,一個是數據結構,一個是操作系統中管理內存的一塊區域分段
 鏈表結構
鏈表結構
3.2 鏈式結構
二叉樹的鏈式存儲結構是指用鏈表來表示一棵二叉樹,即用鏈來指示元素的邏輯關系。
通常的方法是鏈表中每個結點由三個域組成,數據域和左右指針域,左右指針分別用來給出該結點左孩子和右孩子所在的鏈結點的存儲地址。
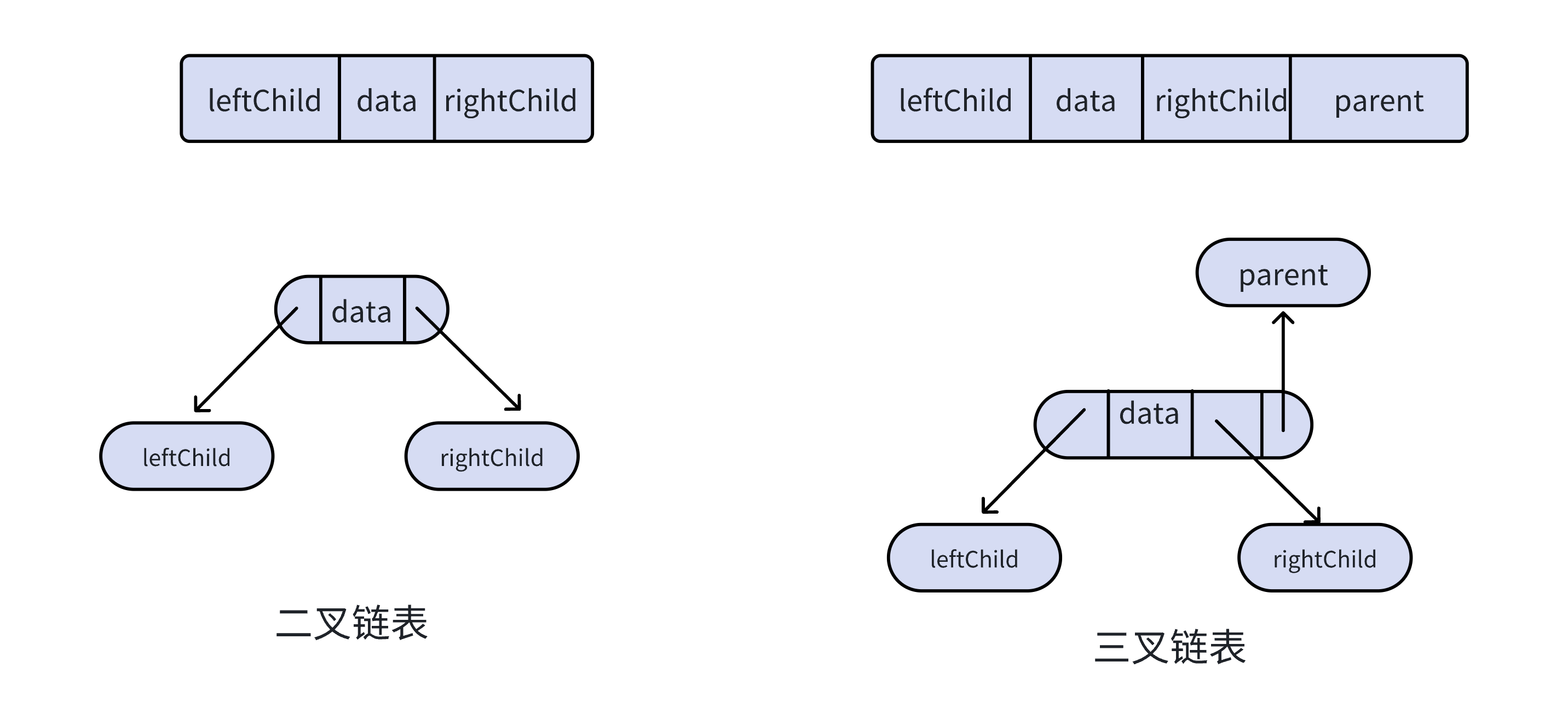
鏈式結構又分為二叉鏈和三叉鏈,當前我們學習中?般都是二叉鏈。后面的學習中會學到高階數據結構如紅黑樹等會用到三叉鏈。
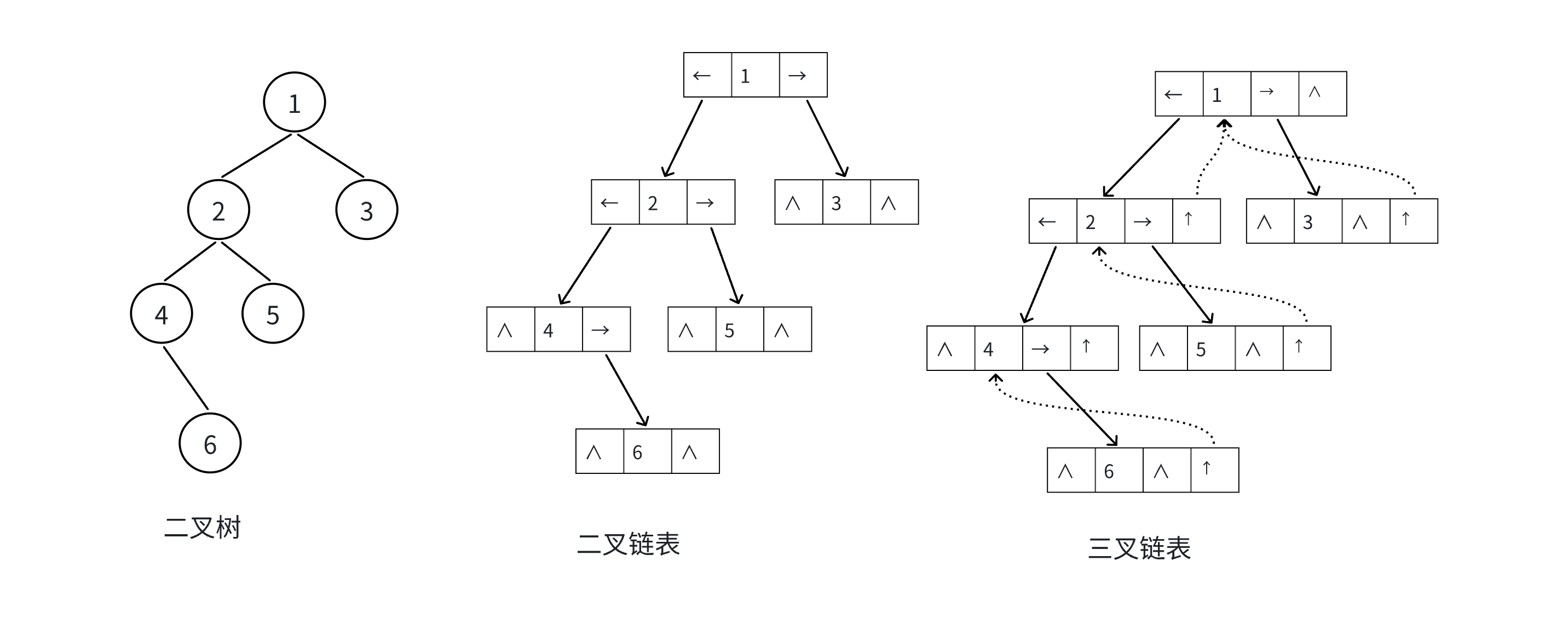

)
:GPIO 輸入之光敏傳感器控制蜂鳴器)








:雨騎古蓮村游記)

TCP擁塞控制與擁塞控制算法深度剖析)
)



![礦物分類系統開發筆記(二):模型訓練[刪除空缺行]](http://pic.xiahunao.cn/礦物分類系統開發筆記(二):模型訓練[刪除空缺行])

