題目一:金幣
題目一:金幣
1.題目來源:
NOIP2015 普及組 T1,難度紅色,入門簽到題。
2.題目描述:

3.題目解析:
問題轉化:求下面的一個數組的前 k 項和。
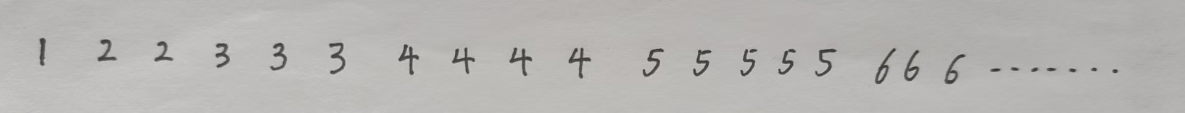
4.算法原理:
模擬
簽到題,只需要進行簡單的模擬就可以了~~~
我們可以定義兩個變量 cur 和 tmp
tmp 表示當前加的是哪一個數。
cnt?表示當前這個數還要加多少次。
仔細觀察,可以發現,1加1次,2加2次,3加3次,……,n加n次。
每加一次某一個數,這個數對應的 cnt --,當 cnt 為 0 時,tmp++, cnt = tmp;
5.代碼實現:
#include <iostream>using namespace std;int main()
{int k; cin >> k;int ret = 0;int tmp = 1; // 當前加的數是 1int cnt = 1; // 當前這個數還需要加 1 次 for(int i = 1; i <= k; i++){ret += tmp;cnt--;if(cnt == 0){tmp++;cnt = tmp;}}cout << ret << endl;return 0;
} 6.總結反思:
在算法競賽中,簽到題是一定要拿滿分的,簽到題要的是快準狠,競賽時千萬不能著急、慌張,想明白之后再寫,遇到 bug 在草稿紙上仔細模擬,再說一遍,千萬不要著急,越著急越錯。
題目二:接水問題
題目二:接水問題
1.題目來源:
NOIP2010普及組T2,難度橙色,簽到題。
2.題目描述:

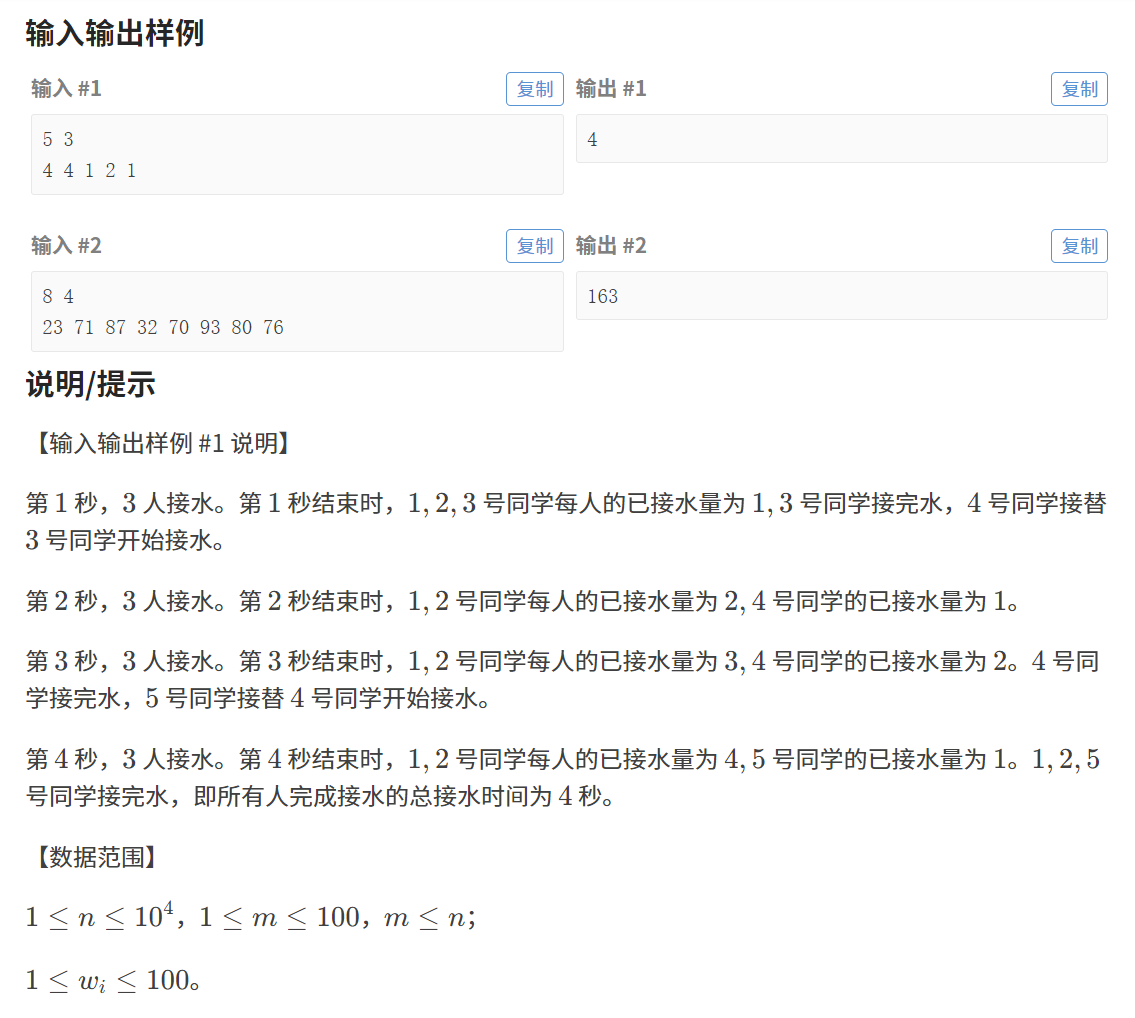
3.題目解析:
這道題,給了我一個深刻的教訓 —— 一定要仔細讀題!!!!!!
我在這道題卡了很長時間,剛開始沒有看到初始接水順序已經確定,以為可以自己安排。朝著貪心方向浪費了很多時間。
這道題其實就是一道簡單的模擬題。直接按照題目模擬即可。
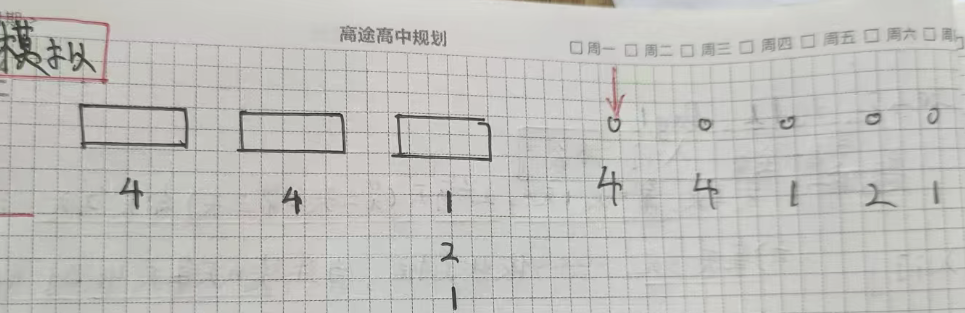
4.算法原理:
模擬+貪心,針對每一位學生,找出所有的水龍頭中,最早結束的那一個,讓他在那里接水。
對于貪心正確性可以用交換論證法來證明。這里是顯然正確的,就不再贅述了。
可以用一個小根堆來模擬,先扔 m 個 0 進去,然后不斷取出堆頂元素,修改后再扔進去。最終結果就是小根堆堆中的最大值。
時間復雜度:O(n log m)
當然了,本題用數組來模擬也是可以的,時間復雜的:O(n * m)
5.代碼實現:
用小根堆來模擬:
#include <iostream>
#include <queue>
#include <vector>using namespace std;int n, m;int main()
{cin >> n >> m;// 小根堆 priority_queue<int, vector<int>, greater<int>> heap;for(int i = 1; i <= m; i++){heap.push(0);}int ret = 0;for(int i = 1; i <= n; i++){int x; cin >> x;int t = heap.top(); heap.pop();t += x;heap.push(t);ret = max(ret, t);}cout << ret << endl;return 0;
}
用數組來模擬:
#include <iostream>using namespace std;const int N = 110;int n, m;
int a[N]; // 存水龍頭使用總時間信息 int main()
{cin >> n >> m;int ret = 0;for(int i = 1; i <= n; i++){int x; cin >> x;int mini = 0; // 要放入的水龍頭的編號int d = 0x3f3f3f3f; // 最小值for(int j = 1; j <= m; j++){if(d > a[j]){d = a[j];mini = j;}} a[mini] += x;ret = max(ret, a[mini]);}cout << ret << endl;return 0;
} 6.總結反思:
簽到題一般不會很難,當發現自己做不出來時,可能是題目理解錯了。
一定要仔細讀題!!!





)
)



)

)



)

Python + 地球信息科學與技術 (GeoICT)=?)
