?2.0 十大排序算法

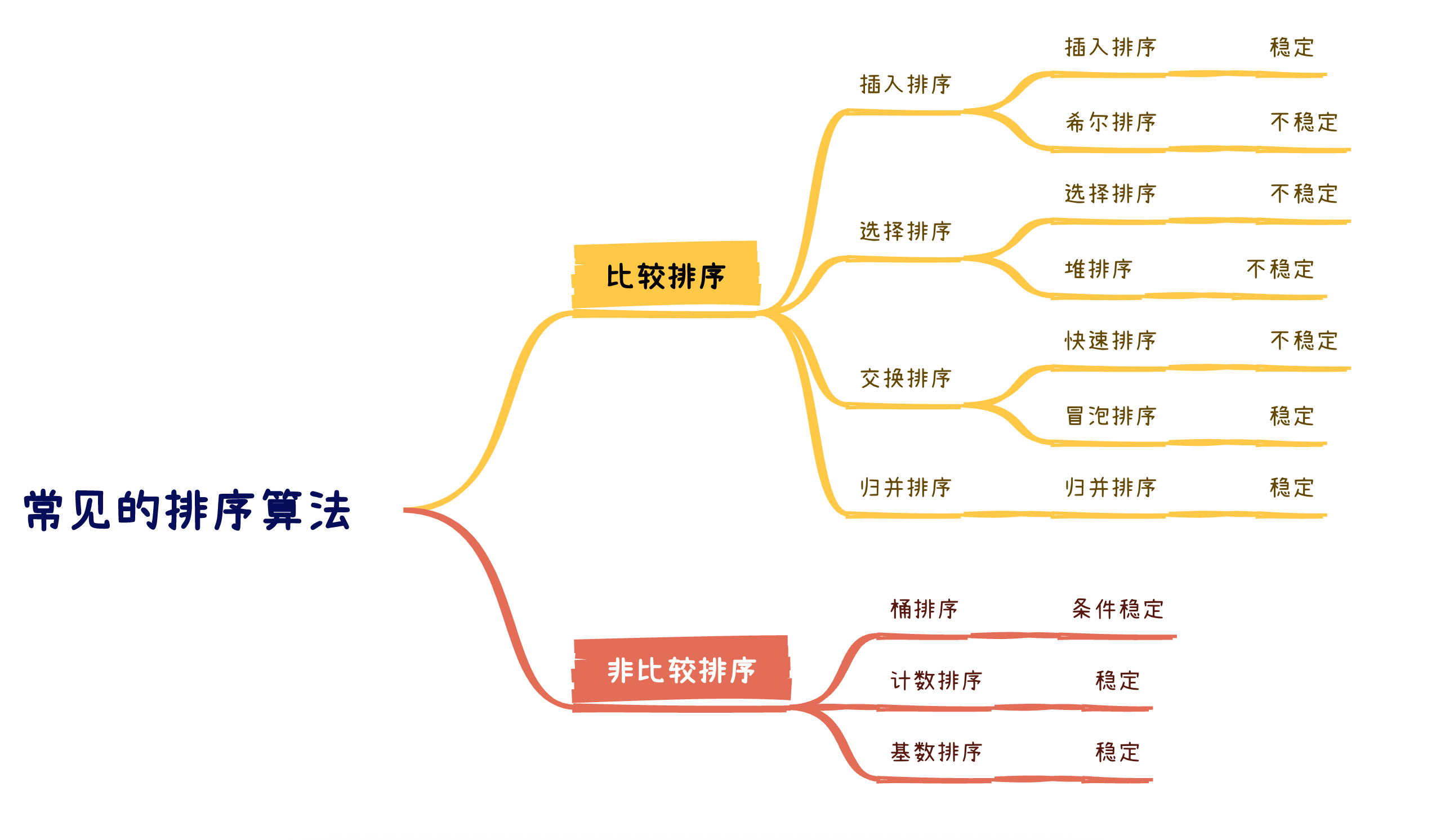
2.5 非比較排序

之前學習的排序算法都是比較排序——借助比較大小，來實現排序。

非比較就是不借助比較大小，來實現排序。——小眾的、局限的

非比較排序大致有這些：計數排序、桶排序、基數排序。

桶排序、基數排序在實踐中意義不大，面試也基本上不會考。

計數排序在實踐中有所應用、校招也會有涉及。

2.5.1 計數排序

基本思想

計數排序又稱為鴿巢原理，是對哈希直接定址法的變形應用。

動圖演示

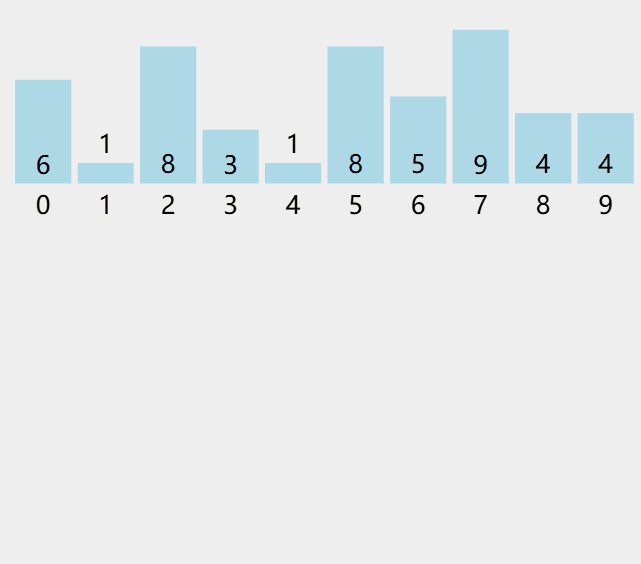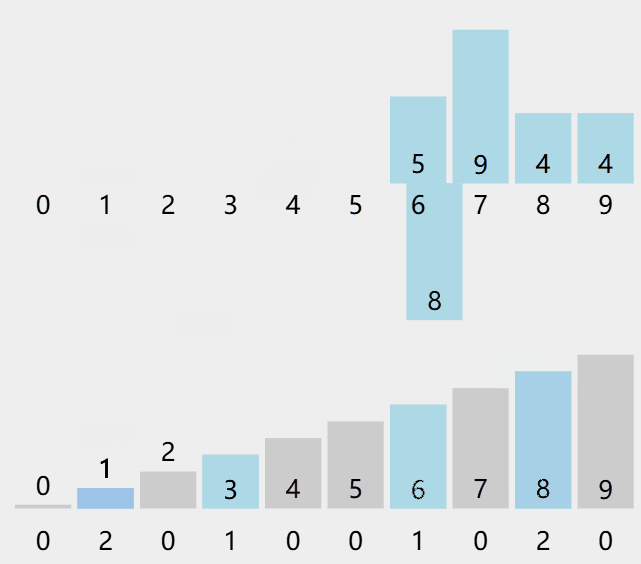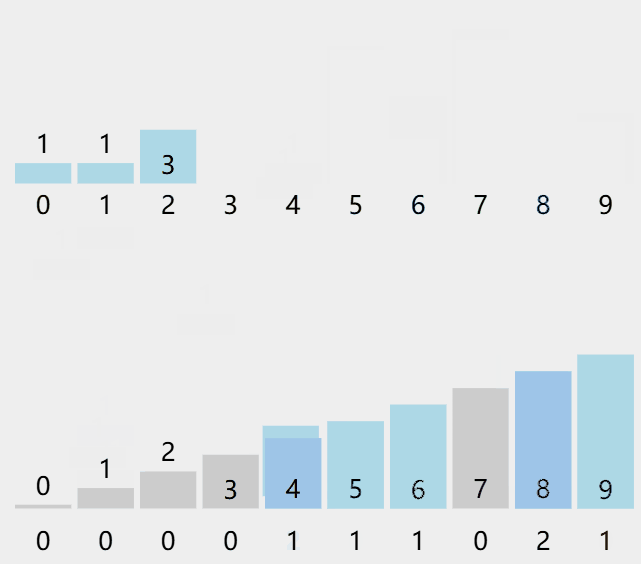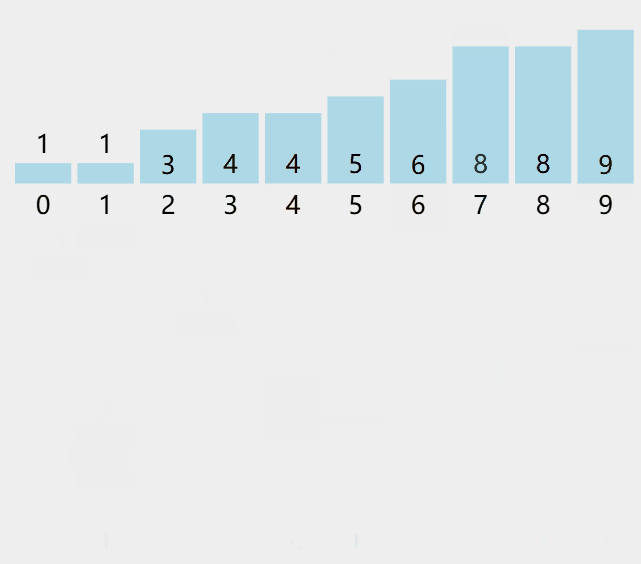
算法步驟

1. 統計相同元素出現次數。

2. 根據統計的結果將序列回收到原來的序列中。

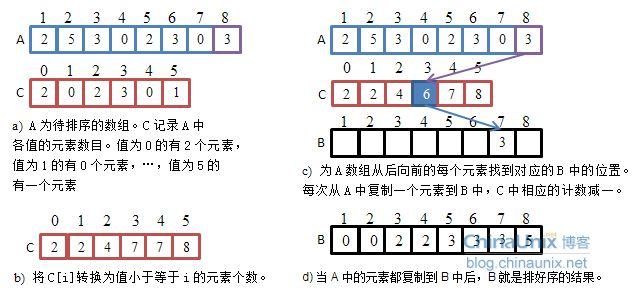
圖解演示。

適合：數據上界、下界差值小(<1000) ——數據范圍集中的數組。

即不管數據大小， 只看數據集不集中。

不做絕對映射——即數據109不必要映射到數組的109位置， 只需要做相對映射。

數組的大小=最大值-最小值+1——找最值：遍歷一遍（還是要比較）。

負數不是問題：min=-5 ——則-5-(-5)=0還是沒問題。

反映射：5 + min = 105。

核心思想不是通過比較來達到有序的，找最值還是需要比較——遍歷一遍O(N)。

代碼實現

//計數排序
void CountSort(int* a, int n)
{//找最值——假設修正法int min = a[0], max = a[0];for (int i = 1; i < n; i++){//如果有更大——就更新一下最大值if (a[i] > max)max = a[i];if (a[i] < min)min = a[i];}//O(N)//0.計算數據范圍int range = max - min + 1;//1.開辟計數數組int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail");return;}memset(count, 0, sizeof(int) * range);//也可以在上面直接calloc——不過calloc的底層邏輯本來就是malloc + memset；//2.統計次數——遍歷原數組——count數組相對位置處值++for (int i = 0; i < n; i++){// （1）統計次數的時候“減”min——“對應”下標位置的值++count[a[i] - min]++;}//3.排序——遍歷count數組，將數據映射回原數組// i控制count遍歷、j控制a遍歷int j = 0;for (int i = 0; i < range; i++){//如果count對應位置不為0——為幾走幾次while (count[i]--)    //--k走k-1次；k--走k次{// 直接覆蓋原數組// （2）還原的時候再把min“加”回來，用下標i加回min就是對應的a中的值a[j++] = i + min;}}
}

時間復雜度：arr數組大小N和count數組大小range當中，較大的那個。

• O(N) 或者 O(range)；
• 或者直接O(N+range)；

顯然當范圍range和數據量在同一量級時，計數排序就是最優排序。——O(N)

測試——100萬個數據（空間不大，大概不到1MB = 2^20 ≈ 10^6，整型就是4MB）

void TestOP()
{srand(time(0));//要產生隨機需要一個種子，否則隨機是寫死的偽隨機const int N = 1000000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){//a1[i] = rand() % 100;a1[i] = rand() % N;                    //產生100個數據——大小都在100萬以內//a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();    //系統啟動到執行到此的毫秒數//InsertSort(a1, N);int end1 = clock();      //系統啟動到執行到此的毫秒數int begin7 = clock();//BubbleSort(a7, N);int end7 = clock();//int begin3 = clock();//SelectSort(a3, N);//int end3 = clock();//ShellSort(a2, N);int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin4 = clock();HeapSort(a4, N);//QuickSort1(a2, 0, N - 1);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();//PrintArray(a4, N);int begin6 = clock();MergeSortNonR(a6, N);int end6 = clock();int begin3 = clock();CountSort(a6, N);int end3 = clock();//printf("InsertSort:%d\n", end1 - begin1);//printf("BubbleSort:%d\n", end7 - begin7);printf("ShellSort:%d\n", end2 - begin2);//printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);//printf("QuickSort1:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("CountSort:%d\n", end3 - begin3);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}int main()
{//TestInsertSort();//TestBubbleSort();//TestShellSort();//TestSelectSort();//TestQuickSort();//TestMergeSort();//TestCountSort();TestOP();//MergeSortFile("sort.txt");return 0;
}

測試結果。

---

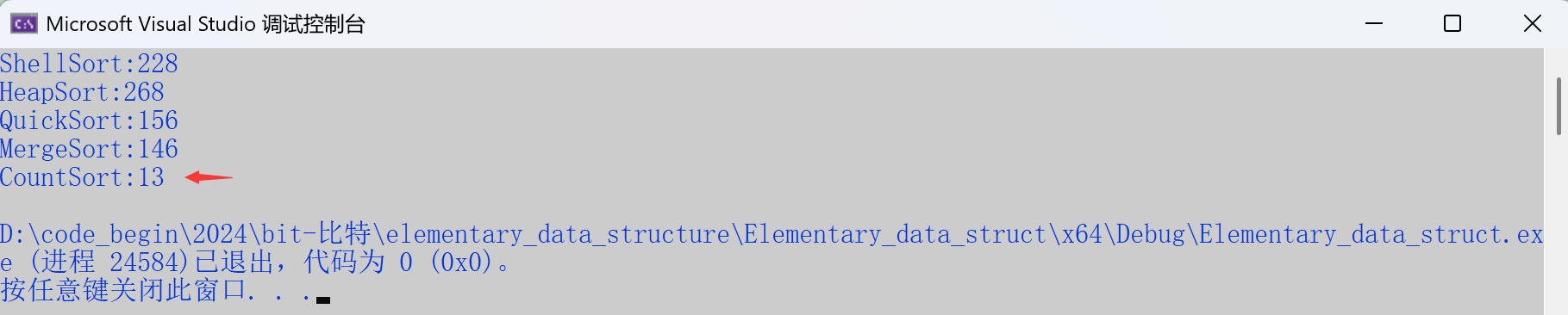
空間復雜度：

• O(range)????????——數據越集中，空間復雜度越小

特性總結

計數排序的特性總結

特性

1. 計數排序在數據范圍集中時，效率很高（幾乎最高），但是適用范圍及場景有限。
2. 時間復雜度：O( MAX(N，range) )
3. 空間復雜度：O(范圍)
4. 穩定性：穩定

局限性

• 數據要集中；
• 只適合整型；
• 有一定空間復雜度；（取決于數據的集中程度）

---

基數排序：先按個位排、再按十位排、再按百位排、……（只適合整型）

桶排序：把元素按區間分桶、桶內再排序，最后按桶順序一次倒出來。（時間和空間都不占優）

---

實踐中排序的對象大多都是結構體，所以計數排序在實踐中的應用并不廣泛。

而比較排序是通用的——只要能比較數據大小就能排——整型、浮點型、字符串、結構體……

---

排序的核心思想還是“比較”

• 比較排序實用性廣 && 大。
• 非比較排序就是小眾的 && 局限的，在特定情境下有自己的實踐意義。

3. 排序算法復雜度及穩定性分析

穩定性：一個數組里面相同的數據，在排序前后的相對位置變不變。

——只排序整型當然沒有意義（兩個5沒差）
——故計數排序不考慮穩定性
——排序結構體就有意義了（兩個5不一樣）

穩定性的應用：

例1：同樣分數的考試成績，先交卷的同學，在排序時名字排在前面。——需要穩定排序

例2：同分數的同學，數學分數高的排名靠前——先按數學排序，再按總分排序。

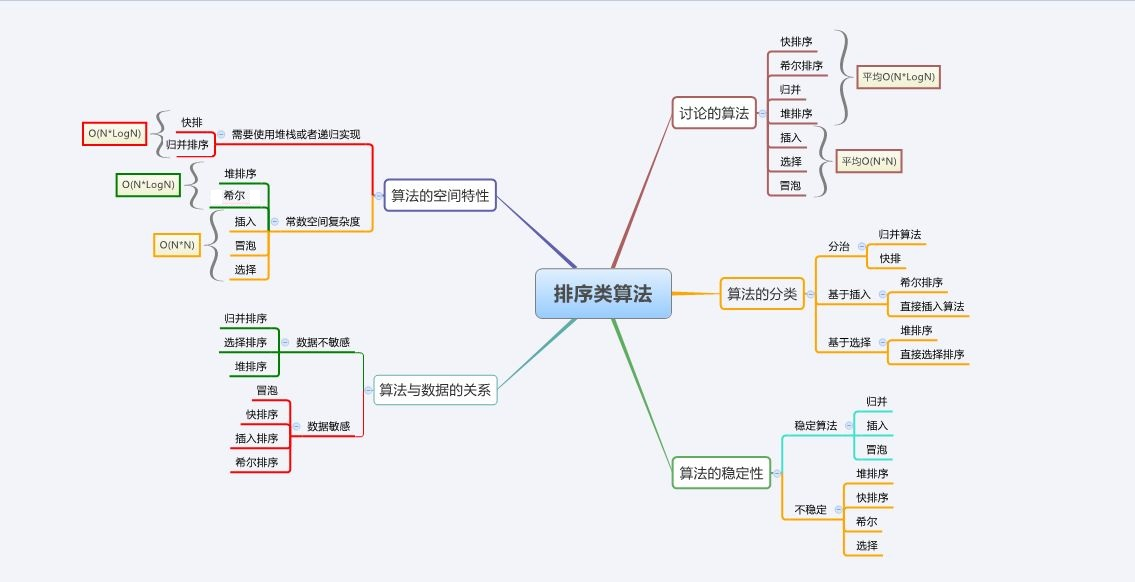
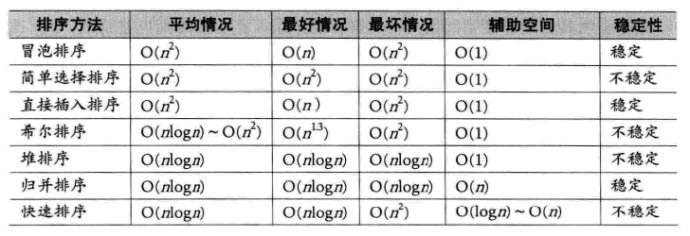
最好不要靠背，要注重理解。

（1）三種O(N^2)的排序算法，只有選擇排序不穩定，空間復雜度都是O(1)。

時間處理上呈現等差數列——>O(N^2)
空間處理上不開額外空間——>O(1)

直接插入排序：相等的時候選擇插入在后面，就穩定。

---

直接選擇排序：乍一想感覺穩定，一些書上也說穩定，實際上不穩定。

選min的時候遇到相等（第二個1）就不更新min，可以保證1穩定。
但是在1和3交換后，就沒辦法保證3穩定。

---

冒泡排序：相鄰比較，大的往后交換，相等就不換——穩定。

（2）一種O(?)的希爾排序，不穩定，空間復雜度O(1)。

希爾排序：相同的數據，預排時可能分到不同的組，就不穩定。

（3）三種O(nlogn)的排序算法，只有歸并穩定，只有堆排序空間復雜度O(1)。

堆排序可以原地操作，不額外開空間
快速排序是遞歸，有空間復雜度的消耗的——要建立logN層棧幀
歸并排序要建立一個輔助歸并數組tmp

堆排序：舉例說明不穩定——5 5 3，升序建好大堆，把第一個5（最大值）放到最后——不穩定。

快速排序：要把key交換到數組中間，比key小的在左邊，比key大的在右邊，和key相等的則在左邊和右邊都可以。

歸并排序：歸并的時候，取小的尾插到tmp數組，相等的時候優先尾插左區間的數據——穩定。
即：左 <= 右，就尾插左。

• “三穩四不穩”
• 只有快速排序、歸并排序有空間復雜度的消耗
• 只有直接插入排序、冒泡排序、無優化快速排序時間復雜度分最好最壞。
  （因為和數據是否有序有關）

整體看來，作為內排序，歸并排序確實和其他幾個一樣有不錯的效率，但是考慮到其必有O(N)的空間復雜度，相比之下還是快速排序更優。

4.?選擇題練習