【狂熱算法篇】探尋圖論幽徑之SPFA算法：圖論迷宮里的閃電尋徑者(通俗易懂版)

??????本篇帶大家探究的是SPFA算法；從基本理解，畫圖分析展示，再到最后的代碼實現，以及為何要這樣實現代碼，等一些細節問題做解釋，相關題型應用，非常值得喲，尤其是剛入門的小白學習；干貨滿滿，通俗易懂；歡迎大家點贊收藏閱讀呀！！！

??歡迎拜訪：羑悻的小殺馬特.-CSDN博客

本篇主題：秒懂百科之SPFA算法的深度剖析

制作日期：2025.08.12

隸屬專欄：?圖論學習專欄? ?美妙的算法世界專欄

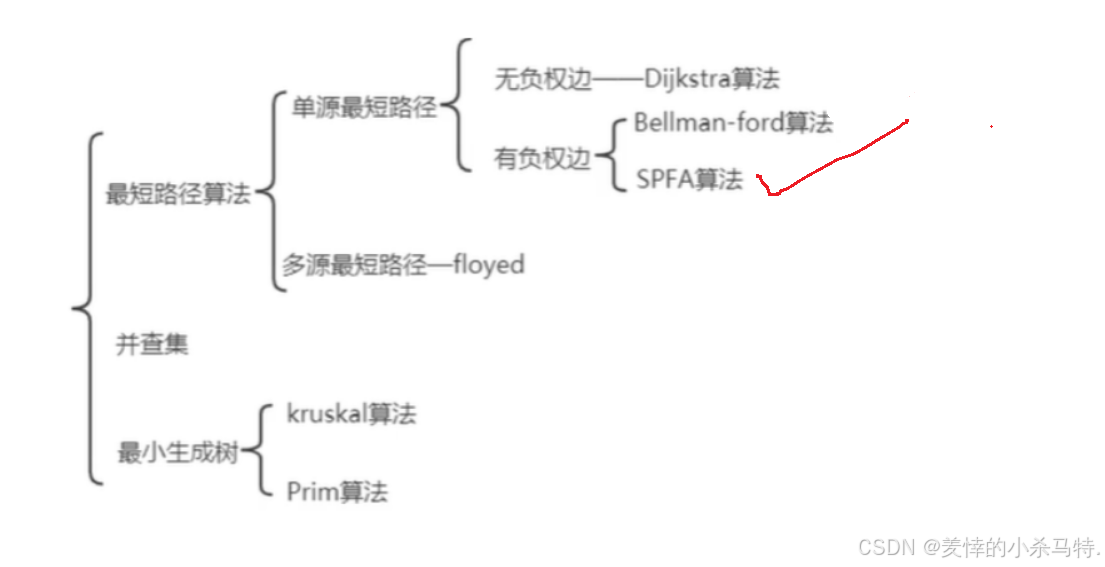
圖論系列算法參考圖：?

目錄：

一·本算法背景：

二·算法核心思想及實例模擬操作：

三.算法詳細步驟:?

3.1初始化操作：

3.2隊列迭代松弛階段：

3.3提速小優化：

3.4檢查是否存在負環：

四.代碼實現：

五·代碼實例測試：

六.小細節及疑點剖析：

6.1 為什么可以通過隊列進行Bellman-Ford算法的優化操作：

6.2 cnt記錄每個點入隊列的次數為什么能實現對負環的判斷：

6.3為什么in_q要記錄某個點是否在隊列里：

七.算法復雜度分析：

7.1時間復雜度：

7.2空間復雜度：

八·SLF優化及LLL優化策略：

8.1SLF（Small Label First）優化：

8.1.1優化原理：

8.1.2實現方式：

8.1.3 SLF優化代碼實現：

8.2LLL（Large Label Last）優化：

8.2.1優化原理：

8.2.2實現方式：

8.2.3LL優化代碼實現：

8.3SLF與LLL聯合優化：

8.3.1優化原理：

8.3.2實現方式：

8.3.3SLF與LLL聯合優化代碼實現：

九.算法優勢與局限性:

9.1優勢：

9.2局限性:

十·應用場景：

10.1交通網絡規劃：

10.2金融套利分析：

10.3社交網絡信息傳播：

10.4競賽與學習：

十一·個人小總結：

一·本算法背景：

在圖論的算法體系中，求解單源最短路徑問題是一個核心且基礎的任務，其在眾多領域有著廣泛且關鍵的應用。SPFA（Shortest Path Faster Algorithm）算法作為這一領域的經典算法之一，憑借自身獨特的優勢，在處理復雜圖結構時發揮著重要作用。它不僅能夠處理包含負權邊的圖，還在平均情況下展現出較高的效率，這使得它在交通規劃、通信網絡優化、經濟決策等多個實際場景中備受青睞。

二·算法核心思想及實例模擬操作：

SPFA 算法本質上是對 Bellman - Ford 算法的一種優化。

Bellman - Ford 算法通過對圖中所有邊進行n-1次松弛操作（n為頂點數）來確定最短路徑，這種方式雖然能保證正確性，但在很多情況下進行了大量不必要的計算。

SPFA 算法則引入了隊列的思想，它只對那些距離可能被更新的頂點進行處理，從而極大地減少了冗余計算。

類似于BFS但是又不全是；它進過隊列的點出去后還可能再次作為最短路徑的中間點等再次入。

總之，就是入隊不一定就是最短路徑的點；還有可能被更新；同時出隊后；還有可能有指向它的點u；借助這個點u到它更近；也就是再次更新這個v的dist使得它再次入隊。?

這里雖然說SPFA算法相對BEllman-Ford算法會快；但是有時候由于圖的特點還是會發生超時等操作；所以使用也需要仔細考慮。?

首先需要的表：

vector<pair<int,int>> v[N]

in_q數組

cnt數組pre數組隊列dsit數組
儲存u點到達的所有v點及其權值的數組（u為起始，v為終止）檢查某個點是否存在隊列記錄每個點進入隊列的次數記錄前驅節點讓可能是最短路徑的點入進來記錄源點距

下面舉例子模擬一下：

完成初始化：

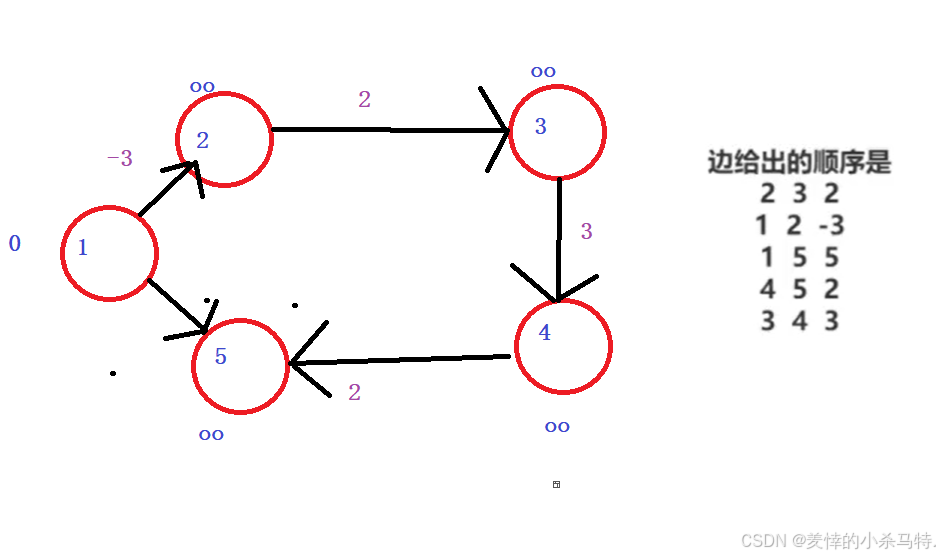
具體操作如圖：

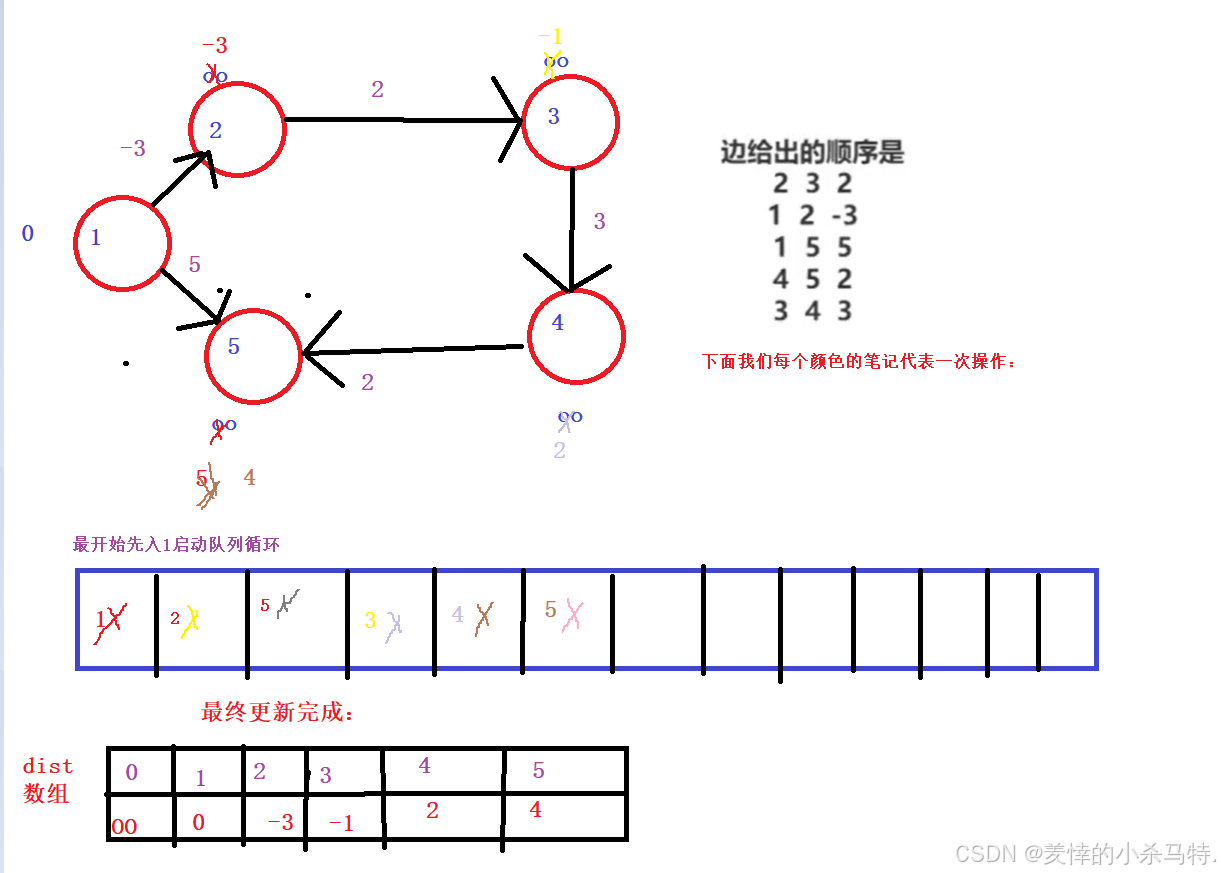
這樣一來其實蠻簡單的吧；當然代碼也是如此；注意一些細節就好啦！?

三.算法詳細步驟:?

下面我們分四步來對代碼進行差分過程；進行相關代碼剖析書寫操作：

3.1初始化操作：

下面我們根據上面的例子及表格完成對應代碼書寫：

初始化鄰接表：

cin >> n >> m;
for (int i = 0; i < m; i++) {int x, y, z;//單雙向邊都可：cin >> x >> y >> z;v[x].emplace_back(y, z);	
}

?初始化pre數組：

void init_pre() {for (int i = 1; i <= n; i++)pre[i] = i;
}

初始化dist：

fill(dist + 1, dist + n + 1, maxi);//初始化dist要注意：我們從1-n的點的編號；也就是初始化這個區間（[迭代器)）

其他；這樣類似的初始化和我們上一篇的Bellman-Ford算法差不多；可以參考：

【狂熱算法篇】探尋圖論幽徑：Bellman - Ford 算法的浪漫征程（通俗易懂版）-CSDN博客

3.2隊列迭代松弛階段：

也就是說只要隊列不存在；然后我們對到達這個p點的邊進行松弛成功了；即此時的路徑有可能是到達p或者通過p到達其他點的最短路徑。
? ? ? 因此可能作為最短路徑及它的一部分；故入隊列；但是還是不太完美；因此就要用到下面的優化了。

	dist[s] = 0;q.push(s);while (!q.empty()) {int cur = q.front();q.pop();for (auto [p,w] : v[cur]) {if (dist[cur] != maxi && dist[cur] + w < dist[p]) {dist[p] = dist[cur] + w;pre[p] = cur;q.push(p);}}}

3.3提速小優化：

記錄是否在隊列中防止重復操作；因為如果隊列有相同的點；那么對一個點操作完只可能改變dist p；自身的dist不會變；也就是當再次遍歷到下一個同點的時候；不會進行任何操作。

所以只需要在上面代碼加上檢查數組即可：

dist[s] = 0;
q.push(s);
in_q[s] = 1;
while (!q.empty()) {int cur = q.front();q.pop();in_q[cur] = 0;for (auto [p,w] : v[cur]) {if (dist[cur] != maxi && dist[cur] + w < dist[p]) {dist[p] = dist[cur] + w;pre[p] = cur;if (!in_q[p]) {// 不在隊列中才入隊q.push(p);in_q[p] = 1;}}}}

3.4檢查是否存在負環：

這里我們先放結論；如果一個點被入隊列次數超過了n次；那么它一定是存在負環的（正環或0環可以提前找到最短路徑；去環無影響；故不可能發生）：

dist[s] = 0;
q.push(s);
in_q[s] = 1;
cnt[s]++;
while (!q.empty()) {int cur = q.front();q.pop();in_q[cur] = 0;for (auto [p,w] : v[cur]) {if (dist[cur] != maxi && dist[cur] + w < dist[p]) {dist[p] = dist[cur] + w;pre[p] = cur;if (!in_q[p]) {// 不在隊列中才入隊q.push(p);in_q[p] = 1;cnt[p]++;if (cnt[p] > n) return 0;//判斷負環}}}}

四.代碼實現：

#include<iostream>
#include<vector>
#include<algorithm>
#include<map>
#include<queue>
using namespace std;
int maxi = 0x3f3f3f3f;
const int N = 1e6 + 1;
int dist[N], n, m;
int pre[N];//前驅節點
vector<pair<int,int>> v[N];//鄰接表：儲存u及所連接的v和之間的w
queue<int>q;
bool in_q[N] = { 0 };//記錄是否在隊列中防止重復操作；因為如果隊列有相同的點；那么對一個點操作完只可能改變dist p；自身的dist//不會變；也就是當再次遍歷到下一個同點的時候；不會進行任何操作。
int cnt[N] = { 0 };//記錄節點入隊列次數；判斷是否出現負環
bool SPFA(int s,int n) {//n個點fill(dist + 1, dist + n + 1, maxi);//初始化dist要注意：我們從1-n的點的編號；也就是初始化這個區間（[迭代器)）dist[s] = 0;q.push(s);in_q[s] = 1;cnt[s]++;while (!q.empty()) {int cur = q.front();q.pop();in_q[cur] = 0;for (auto [p,w] : v[cur]) {//這里為何會入隊列？ //也就是說只要隊列不存在；然后我們對到達這個p點的邊進行松弛成功了；即此時的路徑有可能是到達p或者通過p到達其他點的最短路徑//因此可能作為最短路徑及它的一部分；故入隊列。if (dist[cur] != maxi && dist[cur] + w < dist[p]) {dist[p] = dist[cur] + w;pre[p] = cur;if (!in_q[p]) {// 不在隊列中才入隊q.push(p);in_q[p] = 1;cnt[p]++;if (cnt[p] > n) return 0;//判斷負環}}}}return 1;}void init_pre() {for (int i = 1; i <= n; i++)pre[i] = i;
}
int getpath(int x) {pre[x] == x ? x : getpath(pre[x]);cout << x << " ";return x;
}int main() {cin >> n >> m;for (int i = 0; i < m; i++) {int x, y, z;//單雙向邊都可：cin >> x >> y >> z;v[x].emplace_back(y, z);	}init_pre();bool flag=SPFA(1,n);if (flag) {if (dist[n] == maxi) cout << "unconnected" << endl;else {cout << dist[n] << endl;cout << "最短路徑：" << endl;getpath(n);}}else {cout << "exist negative circle " << endl;}return 0;}

五·代碼實例測試：

下面我們就來用幾組數據測試一下上述的代碼：

①看一下到達6號點最短路徑是不是1；路途是不是1 2 5 6：

?

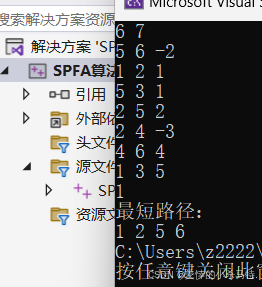
也是成立的。

再測試一下：

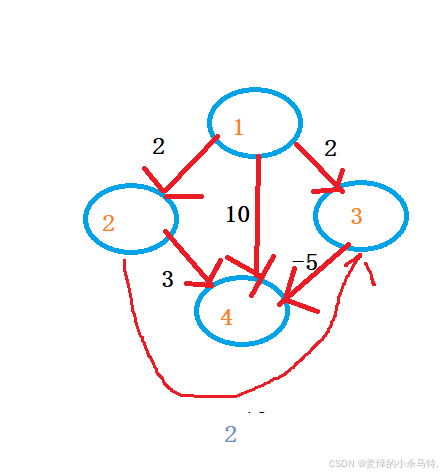
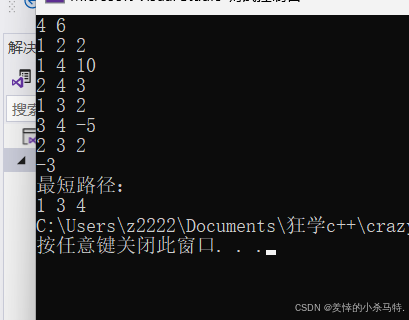
②看一下最終1到4最短路徑是不是-3 路途是不是1 3 4：?

③測試一下負環：

?

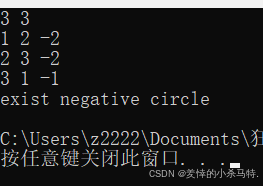
最終也是成立的；但是有些情況SPFA算法有時候會超時；因此選擇的時候還需注意。?

六.小細節及疑點剖析：

我們下面從這幾個可能會有疑惑的點來分析一下：

6.1 為什么可以通過隊列進行Bellman-Ford算法的優化操作：

我們上篇講述了Bellman-Ford算法的原理：對全邊n-1次松弛；但是這樣就算提前結束也肯定會有的邊雖然讓它松弛但是也不會更新dist值；也就是重復操作。

那么我們這里就可以用隊列：比如某個點u松弛后dist更新了也就是它找到了最短路徑或者其他點可以借助這個點u進行找最短路徑;因此把它入隊列方便找到可以借助它作為中間點的其他點v（可能就是最短路徑）。

?這里為何會入隊列？?
也就是說只要隊列不存在；然后我們對到達這個p點的邊進行松弛成功了；即此時的路徑有可能是到達p或者通過p到達其他點的最短路徑因此可能作為最短路徑及它的一部分；故入隊列。

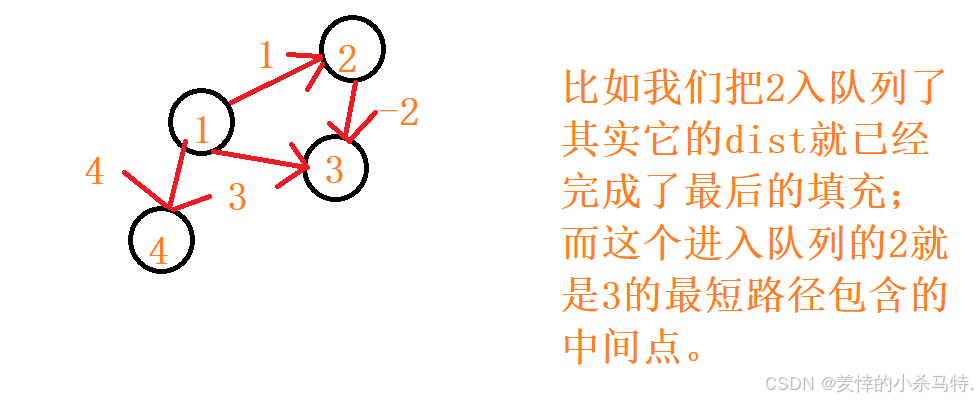
總結一下：凡是入隊列的點要么已經找到了最短路徑要么可能是最短路徑要么其他點可以借助入進的這個點的dist找到自己的最短路徑。?

6.2 cnt記錄每個點入隊列的次數為什么能實現對負環的判斷：

我們SPFA算法同Bellman-Ford算法一樣是可以檢測出負環的；但是這里SPFA是怎么檢測的呢？

我們可以發現當有n條邊的時候；源點到達一個點的最短路徑除了正環和零環（它們的最短路是絕對不包含環的；因為有環只會延長最短路）一定最長是n-1條邊（也就對應著我們Bellman-Ford算法為啥進行n-1次全邊松弛操作了。）；那么此時我們可以得出的結論：

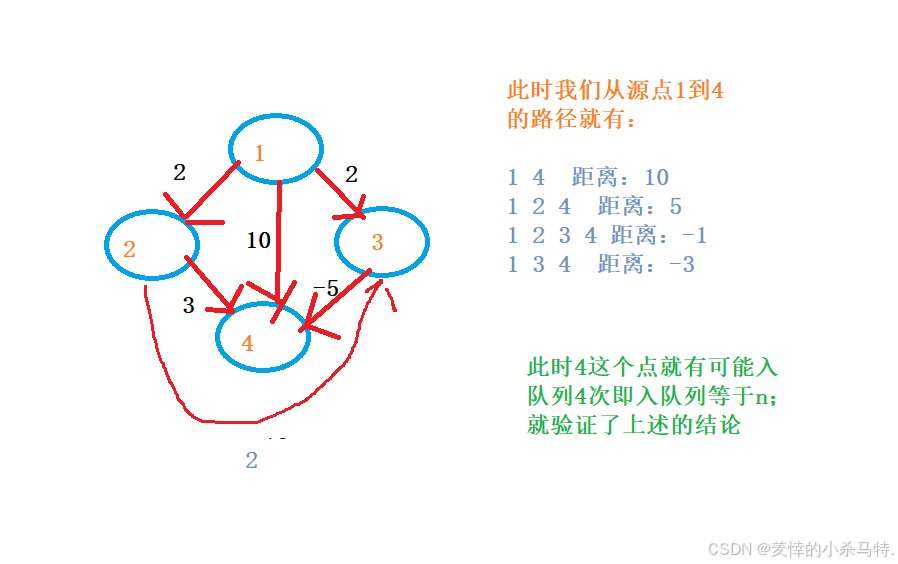
n個點的時候；那么源點到達某個點的路徑最長就是要經過n-1條邊；然后會有最多n條路徑；也就是某個點的dist可能最多被更新n次；也就是最多一個點可能會入隊列n次；也就是我們的如果存在最小路徑的情況下（無環，正環，零環）；因此如果它進入的次數大于n也就說明是負環的情況了。

下面我們就舉一下當恰好一個點入隊列可能達n次的情況：

6.3為什么in_q要記錄某個點是否在隊列里：

其實就是防重復操作：

記錄是否在隊列中防止重復操作；因為如果隊列有相同的點；那么對一個點操作完只可能改變dist p；自身的dist不會變；也就是當再次遍歷到下一個同點的時候；不會進行任何操作。

下面我們舉個例子來說明一下：

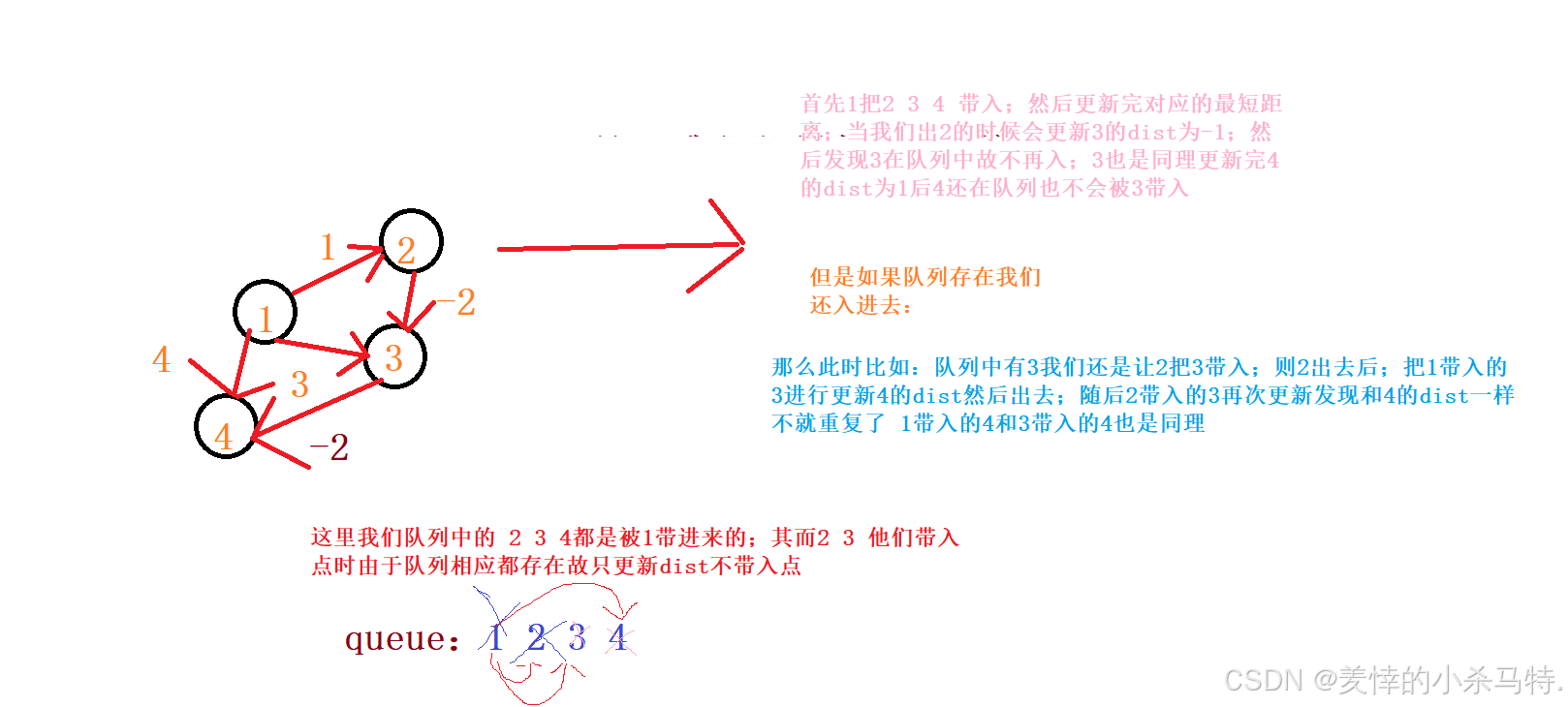
是不是一下子就恍然大悟了哈哈哈！！！?

七.算法復雜度分析：

下面我們從時間和空間兩方面來分析一下：

7.1時間復雜度：

  1. 平均情況：在平均情況下，SPFA 算法的時間復雜度為O(km)，其中是一個較小的常數，通常遠小于頂點數n，m是邊數。這是因為它通過隊列優化，只處理那些可能會更新距離的頂點，避免了 Bellman - Ford 算法中對所有邊的多次無效松弛操作，大大減少了計算量。
  2. 最壞情況：然而，在最壞情況下，比如當圖存在大量負權邊且結構特殊時，SPFA 算法會退化為 Bellman - Ford 算法。此時，它需要對所有邊進行n-1次松弛操作（n為頂點數），時間復雜度變為O(nm)。例如，當圖是一個鏈狀結構且存在負權邊時，SPFA 算法可能會不斷地對鏈上的頂點進行入隊和松弛操作，導致時間復雜度急劇上升。

7.2空間復雜度：

  1. 存儲圖的結構：算法需要存儲圖的鄰接表來表示圖的結構。對于一個有m條邊的圖，存儲鄰接表的空間復雜度為O(m)。
  2. 輔助數組：還需要存儲距離數組dist、頂點是否在隊列中的數組in_q以及入隊次數數組cnt。這些數組的大小都與頂點數n相關，每個數組的空間復雜度為O(n)。因此，總體空間復雜度為O(n+m)。

八·SLF優化及LLL優化策略：

我們不難發現這樣普通的SPFA算法每次只能取到隊頭的元素；這樣有可能dist比較小的不是先取到；導致了本來可以提前確定好最短路徑；或可能是最短路徑的點在后面才會被操作；這樣不就相當于麻煩速度變慢了因此我們可以使用deque根據下面兩個優化方面進行小小優化：

SLF：即插入時候做優化；LLL：選擇元素刪除隊列時做優化。

8.1SLF（Small Label First）優化：

8.1.1優化原理：

在每次取出隊首頂點時，LLL 優化策略會檢查隊首頂點的距離是否大于當前已確定的最短路徑長度的平均值。如果大于，則將隊首頂點移到隊尾，優先處理距離較小的頂點。這樣做可以避免長時間處理距離較大的頂點，防止算法在一些距離較大但對最終結果影響較小的頂點上浪費過多時間，從而提高算法的整體效率。

8.1.2實現方式：

在取出隊首頂點時增加判斷邏輯，根據條件將頂點移到隊尾。實現時需要額外記錄已確定的最短路徑長度之和以及已處理的頂點數，以便計算平均值。

簡單來說就是：這里用雙端隊列進行優化；可以更快的確定某點的最短路徑；提前更新出到某點的可能是的最短路徑；加快了找到真正的最短路徑或者以及找到當前點的最短路徑；以及后序的其他點的最短路的速度。

因此我們只需要在源代碼特判一下：在入隊列的時候和隊頭元素比較一下；如果dist要小于隊頭；那么就插隊頭否則插隊尾。

8.1.3 SLF優化代碼實現：

#include<iostream>
#include<vector>
#include<algorithm>
#include<map>
#include<queue>
using namespace std;
int maxi = 0x3f3f3f3f;
const int N = 1e6 + 1;
int dist[N], n, m;
int pre[N];//前驅節點
vector<pair<int, int>> v[N];
deque<int>q;
bool in_q[N] = { 0 };
int cnt[N] = { 0 };//記錄節點入隊列次數
bool SPFA(int s, int n) {//n個點fill(dist + 1, dist + n + 1, maxi);//初始化dist要注意：我們從1-n的點的編號；也就是初始化這個區間（[迭代器)）dist[s] = 0;q.push_back(s);in_q[s] = 1;cnt[s]++;while (!q.empty()) {int cur = q.front();q.pop_front();in_q[cur] = 0;for (auto [p, w] : v[cur]) {if (dist[cur] != maxi && dist[cur] + w < dist[p]) {dist[p] = dist[cur] + w;pre[p] = cur;if (!in_q[p]) {//這里用雙端隊列進行優化；可以更快的確定某點的最短路徑；提前更新出到某點的可能是的最短路徑//加快了找到真正的最短路徑或者以及找到當前點的最短路徑；以及后序的其他點的最短路的速度if (!q.empty() && dist[p] < dist[q.front()]) {q.push_front(p);}else {q.push_back(p);}in_q[p] = 1;cnt[p]++;if (cnt[p] > n) return 0;}}}}return 1;}void init_pre() {for (int i = 1; i <= n; i++)pre[i] = i;
}
int getpath(int x) {pre[x] == x ? x : getpath(pre[x]);cout << x << " ";return x;
}int main() {cin >> n >> m;for (int i = 0; i < m; i++) {int x, y, z;//單雙向邊都可：cin >> x >> y >> z;v[x].emplace_back(y, z);}init_pre();bool flag = SPFA(1, n);if (flag) {if (dist[n] == maxi) cout << "unconnected" << endl;else {cout << dist[n] << endl;cout << "最短路徑：" << endl;getpath(n);}}else {cout << "exist negative circle " << endl;}return 0;}

8.2LLL（Large Label Last）優化：

8.2.1優化原理：

在每次取出隊首頂點時，LLL 優化策略會檢查隊首頂點的距離是否大于當前已確定的最短路徑長度的平均值。如果大于，則將隊首頂點移到隊尾，優先處理距離較小的頂點。這樣做可以避免長時間處理距離較大的頂點，防止算法在一些距離較大但對最終結果影響較小的頂點上浪費過多時間，從而提高算法的整體效率。

8.2.2實現方式：

在取出隊首頂點時增加判斷邏輯，根據條件將頂點移到隊尾。實現時需要額外記錄已確定的最短路徑長度之和以及已處理的頂點數，以便計算平均值。

簡單來說就是：在符合front處的節點大于平均值的時候；一直把它移動到back處；直到發現小于了；停止；方便后面取得front的時候是相對小的dsit；同slf優化；盡可能先操作較小的dist的點。

也就是：我們每次選擇隊頭元素時候把它的dsit和全隊的dist比較如果小就退出選隊頭得時候就會選它；否則把它干到隊尾；再次比較隊頭和平均值。

8.2.3LLL優化代碼實現：

#include<iostream>
#include<vector>
#include<algorithm>
#include<map>
#include<queue>
using namespace std;
int maxi = 0x3f3f3f3f;
const int N = 1e6 + 1;
int dist[N], n, m;
int pre[N];//前驅節點
vector<pair<int, int>> v[N];
deque<int>q;
bool in_q[N] = { 0 };
int cnt[N] = { 0 };//記錄節點入隊列次數
bool SPFA(int s, int n) {//n個點fill(dist + 1, dist + n + 1, maxi);//初始化dist要注意：我們從1-n的點的編號；也就是初始化這個區間（[迭代器)）dist[s] = 0;q.push_back(s);in_q[s] = 1;cnt[s]++;int sum_dist = 0;  // 隊列中所有節點的距離總和int queue_size = 1;  // 隊列中節點的數量while (!q.empty()) {///LLL優化：在符合front處的節點大于平均值的時候；一直把它移動到back處；直到發現小于了；停止；方便后面取得front的時候是相對小的dsit///同slf優化；盡可能先操作較小的dist的點while (!q.empty() && dist[q.front()] * queue_size > sum_dist) {int front_node = q.front();q.pop_front();q.push_back(front_node);}int cur = q.front();q.pop_front();in_q[cur] = 0;sum_dist -= dist[cur];queue_size--;for (auto [p, w] : v[cur]) {if (dist[cur] != maxi && dist[cur] + w < dist[p]) {dist[p] = dist[cur] + w;pre[p] = cur;if (!in_q[p]) {q.push_back(p);in_q[p] = 1;cnt[p]++;sum_dist += dist[p];queue_size++;if (cnt[p] > n) return 0;}}}}return 1;}void init_pre() {for (int i = 1; i <= n; i++)pre[i] = i;
}
int getpath(int x) {pre[x] == x ? x : getpath(pre[x]);cout << x << " ";return x;
}int main() {cin >> n >> m;for (int i = 0; i < m; i++) {int x, y, z;//單雙向邊都可：cin >> x >> y >> z;v[x].emplace_back(y, z);}init_pre();bool flag = SPFA(1, n);if (flag) {if (dist[n] == maxi) cout << "unconnected" << endl;else {cout << dist[n] << endl;cout << "最短路徑：" << endl;getpath(n);}}else {cout << "exist negative circle " << endl;}return 0;}LLL+SLF的deque優化：

8.3SLF與LLL聯合優化：

8.3.1優化原理：

將 SLF 和 LLL 兩種優化方法結合使用，可以進一步提高算法在各種圖結構下的性能。SLF 策略在入隊時優先處理距離小的頂點，而 LLL 策略在出隊時避免長時間處理距離大的頂點，兩者相互配合，能更有效地減少不必要的計算，加快算法收斂。

8.3.2實現方式：

在代碼中同時實現 SLF 和 LLL 的邏輯。在入隊時采用 SLF 的入隊方式，在出隊時采用 LLL 的判斷和處理方式，通過合理的邏輯組合，充分發揮兩種優化策略的優勢。

還是簡單說一下：我們的LLL和SLF優化都是讓每次選擇隊頭元素的時候操作的盡量是源點距小的點；那么它有可能就是最短源點距；或者其他點可以借助它實現最短源點距的查找從而更快的找到對應的最終的dist值。

歸根結底：就是為了提前操作源點距更小的點；讓每個點的最終dist值盡快更新完；減少點入隊列的次數，提前終止入出隊列操作。

8.3.3SLF與LLL聯合優化代碼實現：

#include<iostream>
#include<vector>
#include<algorithm>
#include<map>
#include<queue>
using namespace std;
int maxi = 0x3f3f3f3f;
const int N = 1e6 + 1;
int dist[N], n, m;
int pre[N];//前驅節點
vector<pair<int, int>> v[N];
deque<int>q;
bool in_q[N] = { 0 };
int cnt[N] = { 0 };//記錄節點入隊列次數
bool SPFA(int s, int n) {//n個點fill(dist + 1, dist + n + 1, maxi);//初始化dist要注意：我們從1-n的點的編號；也就是初始化這個區間（[迭代器)）dist[s] = 0;q.push_back(s);in_q[s] = 1;cnt[s]++;int sum_dist = 0;  // 隊列中所有節點的距離總和int queue_size = 1;  // 隊列中節點的數量while (!q.empty()) {
///LLL優化：在符合front處的節點大于平均值的時候；一直把它移動到back處；直到發現小于了；停止；方便后面取得front的時候是相對小的dsit
// ///同slf優化；盡可能先操作較小的dist的點while (!q.empty() && dist[q.front()] * queue_size > sum_dist) {int front_node = q.front();q.pop_front();q.push_back(front_node);}int cur = q.front();q.pop_front();in_q[cur] = 0;sum_dist -= dist[cur];queue_size--;for (auto [p, w] : v[cur]) {if (dist[cur] != maxi && dist[cur] + w < dist[p]) {dist[p] = dist[cur] + w;pre[p] = cur;if (!in_q[p]) {//這里用雙端隊列進行優化；可以更快的確定某點的最短路徑；提前更新出到某點的可能是的最短路徑
//					//加快了找到真正的最短路徑或者以及找到當前點的最短路徑；以及后序的其他點的最短路的速度if (!q.empty() && dist[p] < dist[q.front()]) {q.push_front(p);}else {q.push_back(p);}in_q[p] = 1;cnt[p]++;sum_dist += dist[p];queue_size++;if (cnt[p] > n) return 0;}}}}return 1;}void init_pre() {for (int i = 1; i <= n; i++)pre[i] = i;
}
int getpath(int x) {pre[x] == x ? x : getpath(pre[x]);cout << x << " ";return x;
}int main() {cin >> n >> m;for (int i = 0; i < m; i++) {int x, y, z;//單雙向邊都可：cin >> x >> y >> z;v[x].emplace_back(y, z);}init_pre();bool flag = SPFA(1, n);if (flag) {if (dist[n] == maxi) cout << "unconnected" << endl;else {cout << dist[n] << endl;cout << "最短路徑：" << endl;getpath(n);}}else {cout << "exist negative circle " << endl;}return 0;}

九.算法優勢與局限性:

9.1優勢：

  1. 可處理負權邊：能應對包含負權邊的圖，像交通網絡中運輸補貼情況，可準確計算最優路徑。
  2. 平均復雜度低：借助隊列優化，平均時間復雜度為O(km) ，在稀疏圖中收斂快。
  3. 能檢測負權環：通過記錄頂點入隊次數判斷負權環，助于金融套利等場景決策。
  4. 實現簡單：基于隊列和松弛操作，代碼結構清晰，適合初學者和快速實現需求。

9.2局限性:

  1. 最壞復雜度高：特殊圖結構下，時間復雜度退化為 O(nm)，運行時間長。
  2. 易被特殊圖卡時：如完全圖會使算法頻繁入隊出隊，降低性能。
  3. 空間開銷大：需隊列及多個數組，大規模圖數據可能內存不足。
  4. 不適用于稠密圖：稠密圖中，隊列和松弛操作多，效率不如專門算法。

十·應用場景：

10.1交通網絡規劃：

①可處理負權邊，能應對道路因特殊活動（如促銷活動帶來運輸補貼）導致成本為負的情況，規劃出最優運輸路徑。

②平均復雜度低，在城市交通等稀疏圖結構中，能快速算出兩點間的最短出行路線。

10.2金融套利分析：

能檢測負權環，可發現金融市場中因匯率差異、利率波動等因素形成的套利機會，輔助投資者決策。

10.3社交網絡信息傳播：

平均復雜度低，適合社交網絡這種稀疏圖，可計算信息從一個用戶到其他用戶的最短傳播路徑，助力精準營銷和信息擴散策略制定。

10.4競賽與學習：

實現簡單，便于初學者理解和快速實現，常用于算法競賽和學習中驗證最短路徑算法的正確性。

還有其他的用途等等；這里就不一一列舉了。?

但是還有些由于它的缺點是不能應用的；如：

  1. 大規模稠密網絡：如集成電路布線問題，SPFA 可能因最壞復雜度高、不適用于稠密圖而效率低下，可考慮使用針對稠密圖優化的算法，如基于鄰接矩陣的 Dijkstra 算法變種。
  2. 超大規模圖數據：在全球互聯網拓撲圖分析中，因空間開銷大可能導致內存不足，可考慮采用分布式算法或內存優化策略。

十一·個人小總結：

本篇我們所介紹的是SPFA算法也就是優化后的Bellman-Ford算法；下面博主總結了一些代碼實現技巧及其適用的歸納；還望對大家學習這個算法有幫助。

實現SPFA：通過鄰接表u連著多個v以及w（權邊）；只要v能借助這個u到達且更新dist（注意u點要是源點可達點）并且v不在隊列就入進去；時刻標記是否在隊列情況以及某點進過隊列的次數cnt。（需要時可維護好pre數組） 這也就是普通SPFA實現。

對應SLF和LLL優化：其實一個是插入隊列的時候：小于隊頭元素就插隊頭大于就插隊尾。

另一個就是選擇隊列中元素的時候，我們每次都要選對頭；因此如果發現隊頭元素的dist小于平均值就放隊尾；否則退出循環選擇它（這樣就實現了每次操作隊列中盡可能dist小的點）

四種最短路徑算法小總結：

?這篇我們的SPFA算法就分享到此；下一篇博主將帶大家剖析其他圖論算法；歡迎大家訂閱呀！！！

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/bicheng/93488.shtml
繁體地址，請注明出處：http://hk.pswp.cn/bicheng/93488.shtml
英文地址，請注明出處：http://en.pswp.cn/bicheng/93488.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

webrtc網頁一對一通話

webrtc網頁一對一通話

基于flutter-webrtc-server做的更改&#xff0c;只使用網頁實現語音和視頻一對一通話&#xff0c;不支持多對多。 項目地址: https://github.com/chging/rtc-server
閱讀更多...
Java調用bat執行python腳本

Java調用bat執行python腳本

1、問題概述&#xff1f;在windows環境中可以通過Java調用bat執行文件&#xff0c;從而調用python腳本&#xff0c;使用起來方便。2、實現方式&#xff1f;2.1、核心代碼bat文件可以在任意位置//獲取文件在項目中的文職 String batFilePathSystem.getProperty("user.dir&q…
閱讀更多...
JavaWeb 歡迎頁設置詳解

JavaWeb 歡迎頁設置詳解

JavaWeb 歡迎頁設置詳解 歡迎頁&#xff08;Welcome Page&#xff09;是用戶訪問 Web 應用根目錄時自動展示的默認頁面。在 JavaWeb 中有多種配置方式&#xff1a;一、配置方式 1. 通過 web.xml 配置&#xff08;傳統方式&#xff09; <web-app><!-- 配置歡迎頁列表 -…
閱讀更多...
反射和類加載機制

反射和類加載機制

一 類加載機制 1.1 加載機制簡介 Java程序從編寫到運行這個過程大致可以分為兩個階段&#xff1a;編譯階段和運行階段。 編譯階段指的是&#xff0c;java源代碼文件**(*.java)被java編譯器&#xff08;javac&#xff09;編譯成字節碼文件(*.class)**的過程。這個過程不需要直接…
閱讀更多...
在CentOS 7 上安裝 MySQL 數據庫

在CentOS 7 上安裝 MySQL 數據庫

文章目錄前言一、使用官方 MySQL 倉庫安裝 MySQL1.1 下載并安裝 MySQL 官方 YUM 倉庫1.2 安裝 MySQL YUM 倉庫1.3 安裝 MySQL1.3.1 補充&#xff1a;1.4 啟動 MySQL 服務1.5 設置 MySQL 服務開機啟動1.6 獲取臨時 root 密碼1.7 配置 MySQL1.7.1 注意事項1.8 完成安裝二、使用默…
閱讀更多...
Linux:套接字

Linux:套接字

從進程的視角來看&#xff0c;網絡通信就是一個主機上的進程和另外一個主機上的進程進行信息傳遞&#xff0c;因此對于操作系統而言&#xff0c;網絡通信就是一種進程間通信的方式。不過這種進程間通信有特殊之處&#xff1a;同一臺主機下可以通過進程ID來標識一個唯一的進程&a…
閱讀更多...
Android init.rc詳解3

Android init.rc詳解3

關于Android Init的詳解&#xff0c;關于Action&#xff0c;Service&#xff0c;Trigger的請參考Android init.rc詳解1&#xff0c;關于Options的請參考Android init.rc詳解2&#xff0c;本章將介紹常見的Commands。 1 Commands bootchart [start|stop] 啟動或停止bootcharti…
閱讀更多...
Sentinel原理之規則管理

Sentinel原理之規則管理

文章目錄1. 基礎知識2. 數據源使用2.1 RedisDatasource2.2 ZookeeperDatasource1. 基礎知識 流量控制規則&#xff08;FlowRule&#xff09;&#xff1a; 閾值類型grade&#xff1a; 0&#xff08;并發線程數&#xff09;&#xff1a;限制同時處理請求的線程1&#xff08;QPS…
閱讀更多...
系統時鐘配置

系統時鐘配置

STM32F103C8T6的系統時鐘配置成72MHZ1. 什么是 STM32 系統時鐘系統時鐘&#xff08;System Clock&#xff09;是整個 MCU&#xff08;微控制器&#xff09;運行的“節拍信號”&#xff0c;所有 CPU 指令執行、外設操作、定時器計時、總線數據傳輸等&#xff0c;都依賴這個時鐘頻…
閱讀更多...
Al大模型-本地私有化部署大模型-大模型微調

Al大模型-本地私有化部署大模型-大模型微調

魔塔社區 魔塔社區平臺介紹 https://www.modelscope.cn/models/Qwen/Qwen2.5-0.5B-Instruct 申請免費的試用機器 如果自己沒有機器 &#xff0c;從這里申請機器 。 下載大模型 pip install modelscope 下載到當前目錄 mkdir -p /root/autodl-tmp/demo/Qwen/Qwen2.5-0.5B-Ins…
閱讀更多...
國內著名AI搜索優化專家孟慶濤發表《AI搜索內容可信度評估綜合指南》

國內著名AI搜索優化專家孟慶濤發表《AI搜索內容可信度評估綜合指南》

近日&#xff0c;國內著名AI搜索優化專家、中國GEO生成式引擎優化領域的開拓者與實踐專家孟慶濤正式發布《AI搜索內容可信度評估綜合指南》&#xff0c;針對當前AI生成內容&#xff08;AIGC&#xff09;在搜索場景中可信度參差不齊的痛點&#xff0c;首次提出覆蓋"技術-內…
閱讀更多...
ruoyi-flowable系統防xss攻擊配置（使用富文本的方式）

ruoyi-flowable系統防xss攻擊配置（使用富文本的方式）

背景。開發小程序過程中。用戶使用富文本的方式比較多。但在傳輸后發現如上傳到系統中的圖片鏈接地址被清空了。問題&#xff1a;想要使用富文本。還需要開啟xss過濾。有什么好的解決方案嗎&#xff1f;解決方案&#xff08;我比較傾向的&#xff09;&#xff1a;通過對富文本內…
閱讀更多...
【opencv-Python學習筆記（2）: 圖像表示；圖像通道分割；圖像通道合并；圖像屬性】

【opencv-Python學習筆記（2）: 圖像表示；圖像通道分割；圖像通道合并；圖像屬性】

目標&#xff1a;1.學會圖像的通道分割與合并2.學會圖像的的常規操作##一些概念&#xff1a;二值圖像&#xff1a;只包含黑色和白色兩種顏色的圖像&#xff0c;1為白色&#xff0c;0為黑色灰度圖像&#xff1a;計算機會將灰度處理為256個灰度級&#xff0c;用區間[0,255]來表示…
閱讀更多...
Qt——常用Widget（控件）

Qt——常用Widget（控件）

常用控件 Widget 需要說明&#xff0c;此處說明的控件都繼承于QWiget&#xff0c;因此之前所說的控件屬性&#xff0c;和相關API&#xff0c;在這里的控件都適用 文章目錄常用控件 Widget按鈕類控件QPushButtonQRadioButtonQCheckBox顯示類控件QLabel初識事件LCD NumberProgre…
閱讀更多...
Cursor/VSCode/VS2017 搭建Cocos2d-x環境，并進行正常的調試和運行（簡單明了）

Cursor/VSCode/VS2017 搭建Cocos2d-x環境，并進行正常的調試和運行（簡單明了）

作者&#xff1a;求一個demo 版權聲明&#xff1a;著作權歸作者所有&#xff0c;商業轉載請聯系作者獲得授權&#xff0c;非商業轉載請注明出處 內容通俗易懂&#xff0c;沒有廢話 廢話不多說&#xff0c;我們直接開始------>>>>>> &#xff01;&#xff…
閱讀更多...
從 LLM 到自主 Agent：OpenCSG 打造開源 AgenticOps 生態

從 LLM 到自主 Agent：OpenCSG 打造開源 AgenticOps 生態

從 LLM 到自主 Agent&#xff1a;OpenCSG 打造開源 AgenticOps 生態在產業拐點上&#xff0c;交付可持續、可落地的智能體未來在生成式 AI 的時代洪流中&#xff0c;大語言模型&#xff08;LLM&#xff09;已成為行業標配&#xff0c;但如何突破“會說不會做”的局限&#xff0…
閱讀更多...
黑馬程序員mysql課程中在Linux系統中安裝mysql出現問題

黑馬程序員mysql課程中在Linux系統中安裝mysql出現問題

問題描述在安裝linux的最后一步的指令的時候報錯警告&#xff1a;mysql-community-server-8.0.26-1.el7.x86_64.rpm: 頭V3 DSA/SHA256 Signature, 密鑰 ID 5072e1f5: NOKEY 錯誤&#xff1a;依賴檢測失敗&#xff1a;net-tools 被 mysql-community-server-8.0.26-1.el7.x86_64 …
閱讀更多...
「iOS」————APP啟動優化

「iOS」————APP啟動優化

iOS學習APP的啟動流程啟動流程缺頁錯誤主要階段pre-main階段main階段啟動優化pre-mainmain階段啟動優化總結流程總結APP的啟動流程 啟動 首先我們來了解啟動的概念&#xff1a; 廣義上的啟動是點擊圖標到首頁數據加載完畢狹義上的啟動是點擊圖標到啟動圖完全消失的第一幀 啟…
閱讀更多...
知名車企門戶漏洞或致攻擊者遠程解鎖汽車并竊取數據

知名車企門戶漏洞或致攻擊者遠程解鎖汽車并竊取數據

漏洞概況一家大型汽車制造商的在線系統存在安全漏洞&#xff0c;可能導致客戶數據泄露&#xff0c;并允許攻擊者遠程訪問車輛。該漏洞由安全研究員Eaton Zveare發現&#xff0c;他已于2025年2月向涉事車企報告并促使漏洞修復。Zveare雖未公開車企名稱&#xff0c;但透露這是在美…
閱讀更多...
Elasticsearch JS 自定義 ConnectionPool / Connection / Serializer、敏感信息脫敏與 v8 平滑遷移

Elasticsearch JS 自定義 ConnectionPool / Connection / Serializer、敏感信息脫敏與 v8 平滑遷移

0. 什么時候該用“高階配置”&#xff1f; 復雜網絡/路由需求&#xff1a;自定義“健康節點”判定、權重路由、多租戶隔離。替換 HTTP 棧&#xff1a;接入企業內網網關、打通自研代理/審計、細化超時/連接細節。序列化治理&#xff1a;為超大 JSON、Bulk、查詢串做定制編碼/壓縮…
閱讀更多...
最新文章

Copyright @ 2022~2023