一、二叉樹

1、樹

?? 1）概念? ? ? ??

????????樹是 n(n >= 0) 個結點的有限集合。若 n=0 ，為空樹。

? ? ? ? 在任意一個非空樹中：

? ? ? ? ? （1）有且僅有一個特定的根結點；

? ? ? ? ? （2）當 n>1 時，其余結點可分為 m 個互不相交的有限集合T1、T2......Tm，其中每一個集合又是一個樹，并且稱為子樹。

? ?2）度、度數、深度

? ? ? ? 結點擁有子樹的個數稱為結點的度。度為 0 的結點稱為葉結點；度不為 0 稱為分支結點。

? ? ? ? 樹的度數：指在這顆樹中，最大的結點的度數，稱為樹的度數。

? ? ? ? 樹的深度（高度）：指從根開始，根為第一層，根的孩子為第二層，即樹的層數，稱為樹的深度。

? ? ? ? 樹的存儲：順序結構、鏈表結構。

2、二叉樹（binary tree）

? 1）概念

? ? ? ? 二叉樹是 n 個結點的有限集合，集合要么為空樹，要么由一個根節點和兩棵互不相交的樹組成，這兩棵樹分別稱為根節點的左子樹和右子樹。

? 2）特點

? ? ?（1）每個結點最多兩個子樹。

? ? ?（2）左子樹和右子樹是有順序的，次序不能顛倒。

? ? ?（3）如果某個結點只有一個子樹，也要區分左、右子樹。

??3）特殊的二叉樹

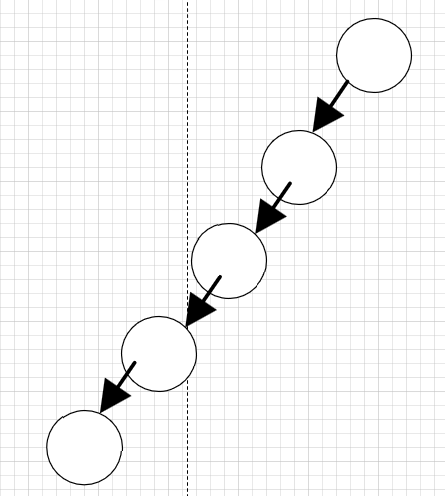
? ?? （1）斜樹

? ? ? ? 斜樹分為兩種，一種是所有的結點都只有左子樹，稱為左斜樹；另一種是所有的結點都只有右子樹，稱為右斜樹。

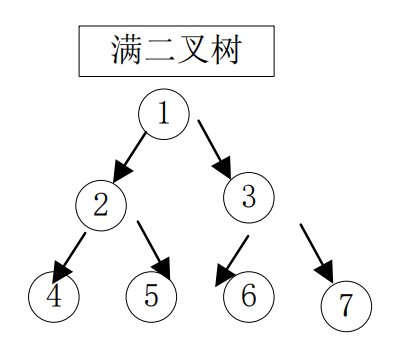
? ? ? ? （2）滿二叉樹

? ? ? ? 滿二叉樹是指所有的分支結點都存在左右子樹，并且葉子都在同一層上。

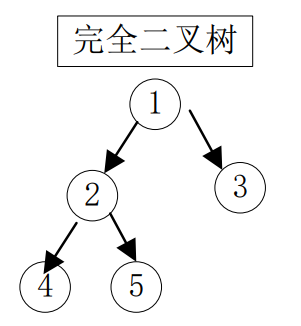
? ? ? ??（3）完全二叉樹

? ? ? ? 完全二叉樹是指：對于一顆具有 n 個結點的二叉樹按照層序編號，如果編號 i( 1<= i <= n )的結點于同樣深度的滿二叉樹中編號為 i 的結點在二叉樹中的位置完全相同，則此樹稱為完全二叉樹。

? ??4）特性

? ? ? ?（1）在二叉樹的第 i 層上最多有 2^(i-1) 個結點，i >= 1。

? ? ? ?（2）深度為 k 的二叉樹至多有 2^k-1 個結點，k >= 1。

? ? ? ?（3）任意一個二叉樹T，如果其葉子結點的個數為 N，度數為 M，則 N=M+1。

? ? ? ?（4）有 n 個結點的完全二叉樹深度為（logn / log2）+ 1。

? ?5）層序

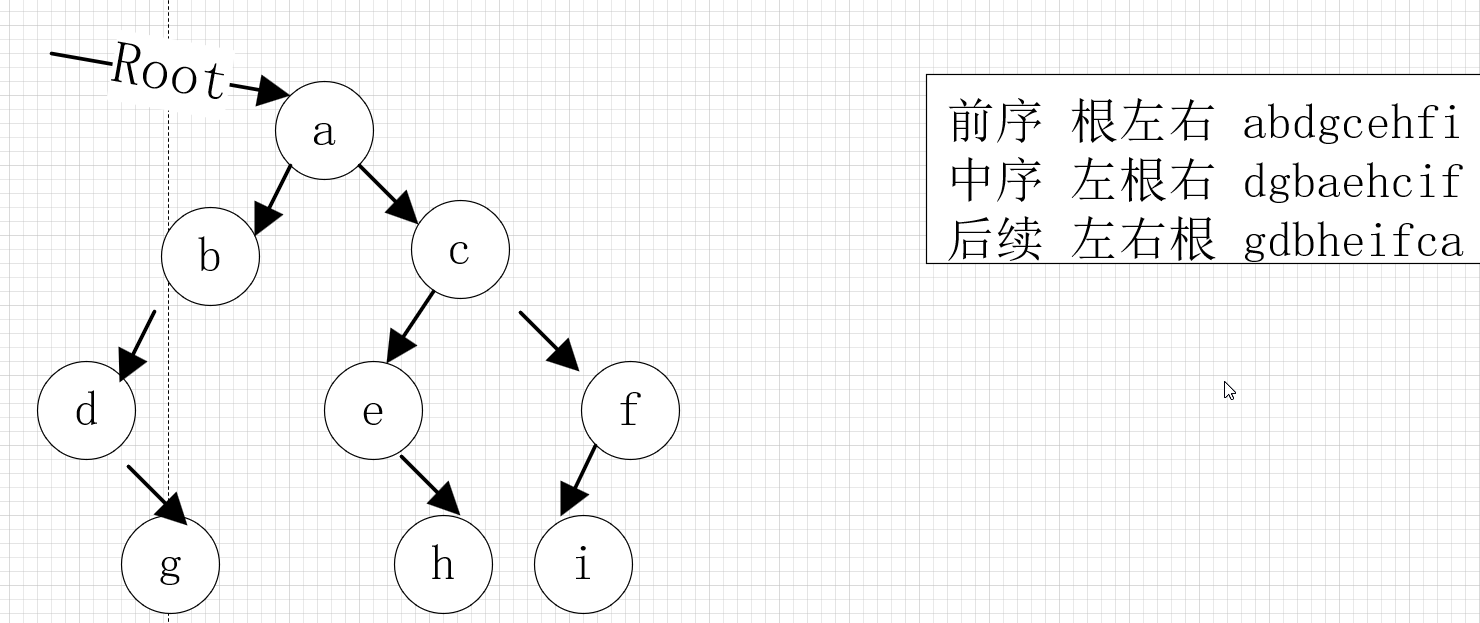
? ? ? ? 前序：根左右。先訪問根結點，再訪問左結點，最后訪問右結點。

? ? ? ? 中序：左根右。先從根結點開始（不是先訪問根結點），從左結點開始訪問，再訪問根結點，最后訪問右結點。

? ? ? ? 后序：左右根。先從根結點開始（不是先訪問根結點），從左結點開始訪問，再訪問右結點，最后訪問根結點。

?????6）二叉樹的函數應用

? ? ? ? （1）創建二叉樹函數

void CreateTree(BiTNode **root)
{char c = data[ind++];if('#' == c){*root = NULL;return ;}else{*root = malloc(sizeof(BiTNode));if(NULL == *root){printf("malloc error\n");*root = NULL;return ;}(*root) -> data = c;CreateTree(&(*root) -> ichild);CreateTree(&(*root) -> rchild);}return ;
}

? ? ? ?（ 2）根左右（前序）函數封裝

//根左右
void PreOrderTraverse(BiTNode *root)
{if(NULL == root){return ;}else{printf("%c", root -> data);PreOrderTraverse(root -> ichild);PreOrderTraverse(root -> rchild);}return ;
}

? ? ? （? 3）左根右（中序）函數封裝

//左根右
void InOrderTraverse(BiTNode *root)
{if(NULL == root){return ;}InOrderTraverse(root -> ichild);printf("%c", root -> data);InOrderTraverse(root -> rchild);return ;
}

? ? ? ? （4）左右根（后序）函數封裝

//左右根
void PostOrderTraverse(BiTNode *root)
{if(NULL == root){return ;}PostOrderTraverse(root -> ichild);PostOrderTraverse(root -> rchild);printf("%c", root -> data);return ;
}

? ? ? ? （5）二叉樹銷毀函數封裝

//銷毀
void DestroyTree(BiTNode *root)
{if(NULL == root){return ;}DestroyTree(root -> ichild);DestroyTree(root -> rchild);free(root);return ;
}

? ? ? ?（ 6）頭文件與其余聲明

#include <stdio.h>
#include <string.h>
#include <stdlib.h>typedef char DATATYPE;typedef struct BiTNode
{DATATYPE data;struct BiTNode *ichild, *rchild; 
}BiTNode;char data[] = "Abd#g###ce#h##fi###";
int ind = 0;

? ? ? ?（ 7）主函數運行格式

int main(int argc, char **argv)
{BiTNode *root;CreateTree(&root);PreOrderTraverse(root);printf("\n");InOrderTraverse(root);printf("\n");PostOrderTraverse(root);printf("\n");DestroyTree(root);root = NULL;return 0;
}

二、gbd調試指令

? ? ? ? gdb 調試指令用來尋找段錯誤。

1、一般調試

? ? ? 1）gcc -g 文件名

? ? ??2）gbd ./a.out （a.out 為該函數的可執行文件）

? ? ??3）b? 函數名???設置斷點，運行到這個函數位置，程序自動暫停

? ? ? ? ? ? ? b? ?數字? ? ?運行到 main函數的這一 “數字” 行，程序自動暫停

? ? ? 4）r? 運行

? ?? ?5）n? 執行下一步（行）步過，若是函數，直接調用結束

? ? ??6）p? 使用p命令，查看變量或指針等數據，p a(變量); p *a(指針)

2、其他相關命令

? ? ??1）bt? 與 where? 顯示棧結構，函數的調用關系

? ? ? 2）s? 步入，如果是函數，進入函數

? ? ??3）c? 跳出循環，在循環后面設置斷點，然后按 c 可返回調用處

? ? ? 4）display? 和 p 相似，一直顯示變量

? ? ? 5）q? 退出 gbd 操作界面

三、各類排序算法的時間復雜度

1、概念

? ? ? ? 時間復雜度是衡量算法執行效率的重要指標，描述了算法的運行時間隨輸入規模（n）增長而變化的趨勢，而非具體的運行時間。

2、推導大O階方法

? ? ? ? 1）用常數 1 取代運行時間中的所有加法常數。

? ? ? ? 2）在修改后的運行次數函數中，只保留最高階項。

? ? ? ? 3）如果最高階項存在且不是 1 ，則去除與這個項相乘的常數。

得到的結構就是大O階。

3、表示方法

? ? ? ? 采用大O符號（Big O Notation）來表示，忽略了常數項、低階項和系數，只保留對增長趨勢影響最大的項。例如下圖：（圖中 階 代表時間復雜度）

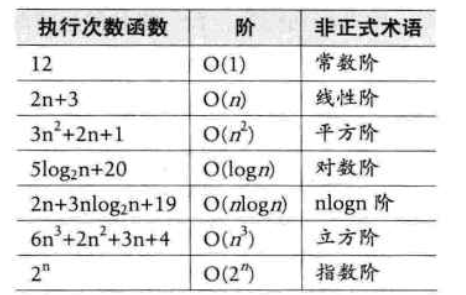
4、常見時間復雜度（按效率高到低排序）

? ?1）常數階 O(1)

? ? ? ? 算法執行時間不隨規模 n 變化，始終為固定步驟，如訪問數組中的某個元素。

? ?2）對數階 O(log n)

? ? ? ? 執行時間隨 n 增長，但增長速度極慢（每步可將問題規模縮小一半），如二分查找。

? ?3）線形階 O(n)

? ? ? ? 執行時間與 n 成正比例增長，如線性查找。

? ?4）線形對數階 O(n log n)

? ? ? ? 效率介于 O(n) 和 O(n^2) 之間，常見于高效排序算法，如快速排序、歸并排序。

? ?5）平方階 O(n^2)

? ? ? ? 執行時間與 n 的平方成正比，適用于小規模數據，如冒泡排序。

?? 6）指數階 O(2^n)、階乘階 O(n!)4

? ? ? ? 效率極低，隨 n 增長，執行時間呈爆炸式增長，僅適用于極小規模數據。

5、各類算法時間復雜度整理

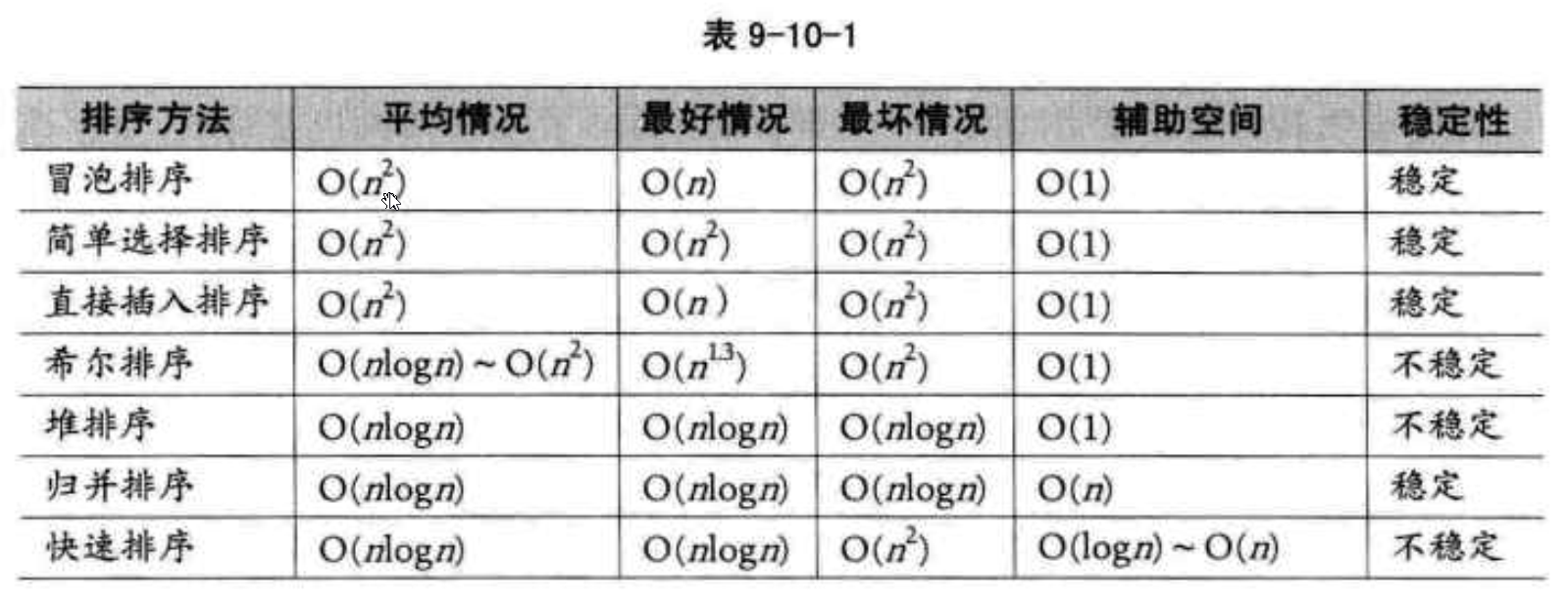
常用的時間復雜度所耗費的時間從小到大依次是：

【END】