-----------------------------------------------------------------------------------------------
這是我在我的網站中截取的文章,有更多的文章歡迎來訪問我自己的博客網站rn.berlinlian.cn,這里還有很多有關計算機的知識,歡迎進行留言或者來我的網站進行留言!!!
-----------------------------------------------------------------------------------------------
?
一、邏輯回歸的含義
邏輯回歸(Logistic Regression)是一種用于解決分類問題的統計學習方法,尤其適用于二分類任務(如判斷“是/否”)。它通過Sigmoid函數將線性回歸的輸出映射到[0,1]區間,表示樣本屬于某一類的概率。
通俗理解
可以把邏輯回歸想象成一個“概率打分器”:它先像線性回歸一樣計算輸入特征的加權和(比如“年齡+收入”),然后通過一個“S型魔法函數”(Sigmoid)把這個分數壓縮成0到1之間的概率。例如,輸出0.7表示“有70%的可能性是貓,30%的可能性是狗”。
二、二分類問題
-
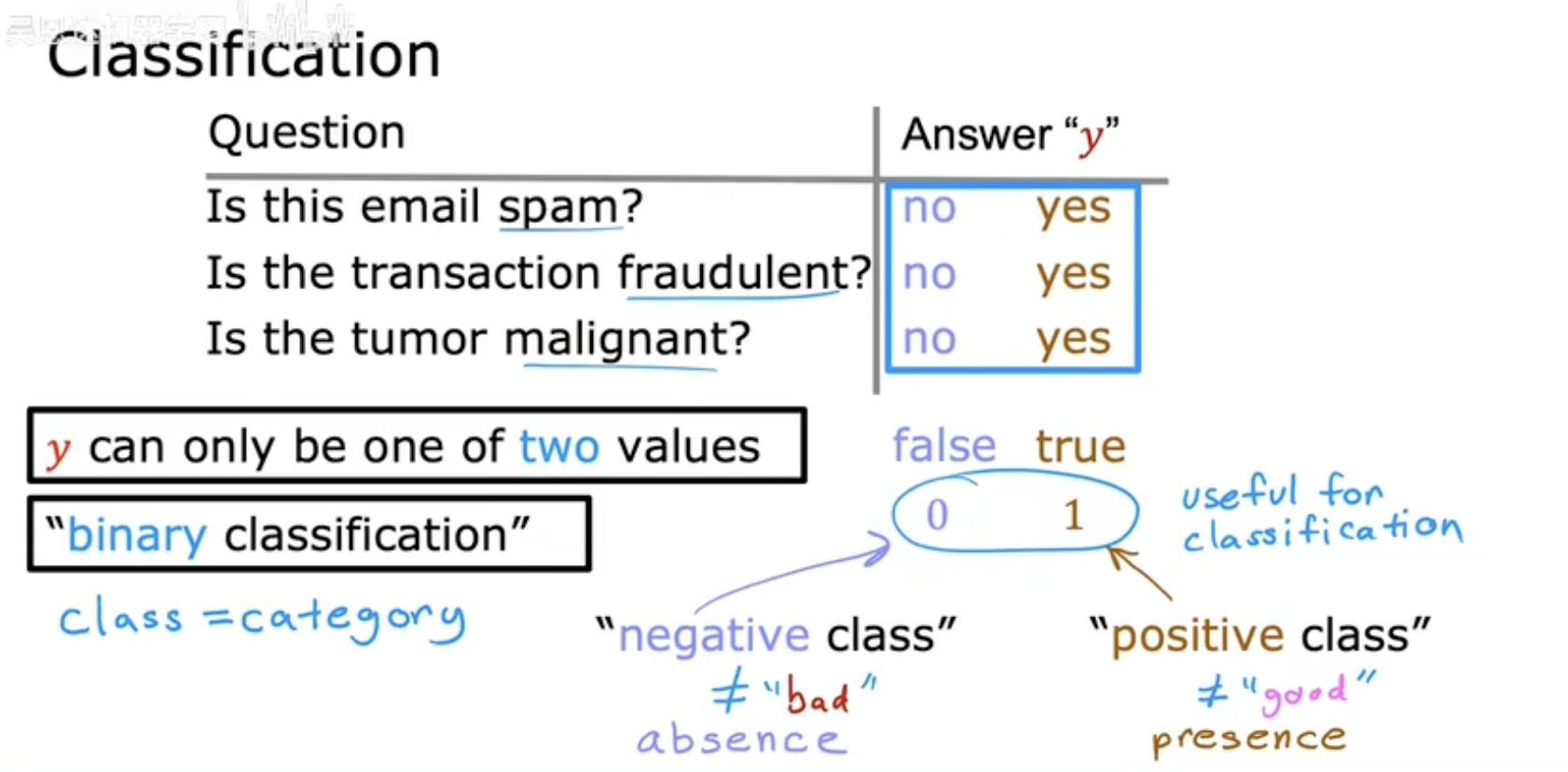
任務示例:圖中列舉了典型的二分類場景,如判斷郵件是否為垃圾郵件(spam)、交易是否欺詐、腫瘤是否惡性。
-
輸出(y):分類結果只能是兩個互斥的值,例如“是/否”(yes/no)、“真/假”(true/false),或用數值“0/1”表示(0=負類,1=正類)。
-
類別術語:
-
負類(Negative Class):通常表示“無”或默認狀態(如“非垃圾郵件”)。
-
正類(Positive Class):關注的目標(如“欺詐交易”)。
-
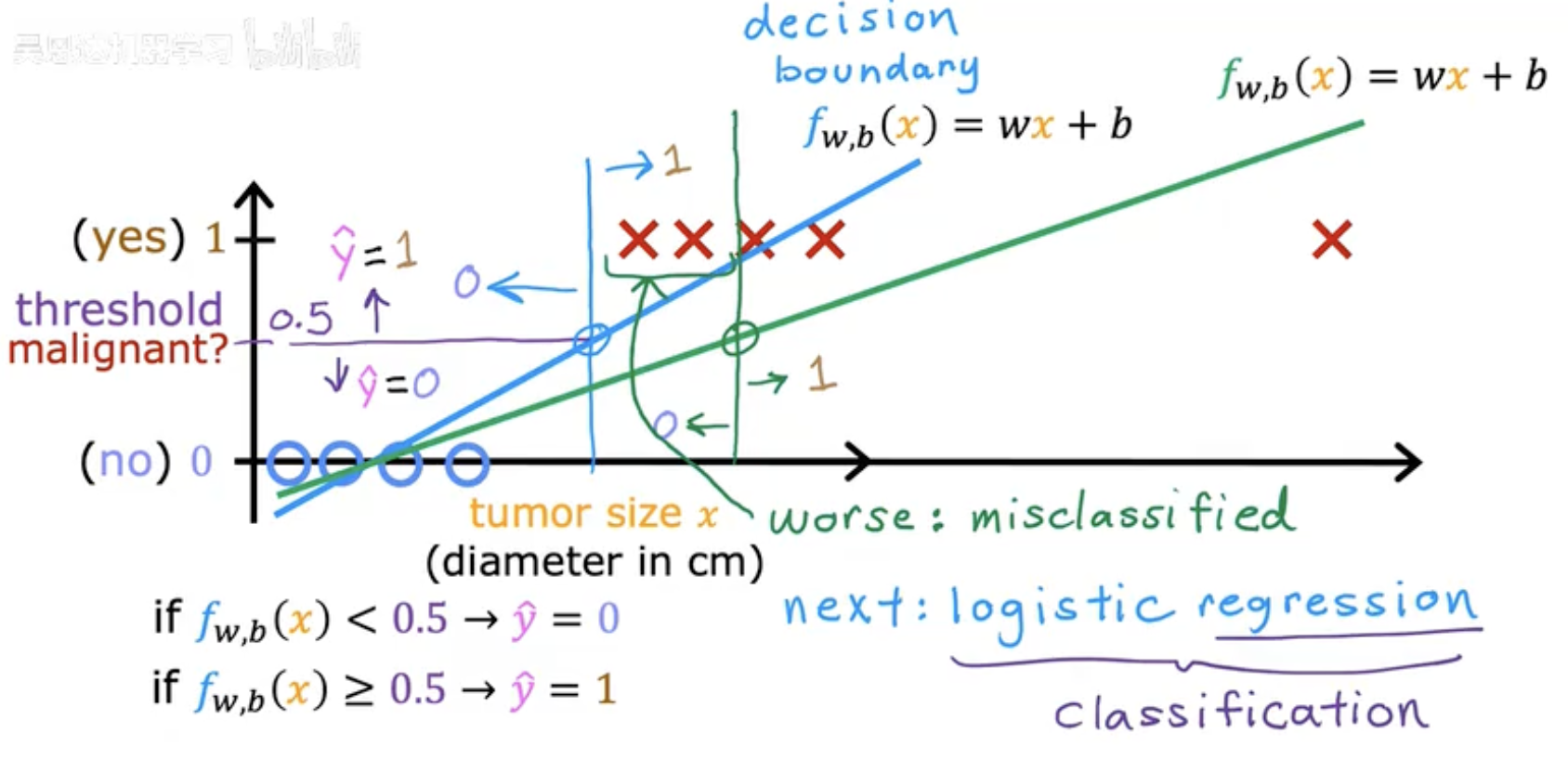
這幅圖展示了線性分類(如邏輯回歸)在判斷腫瘤是否惡性的原理:
-
橫軸是腫瘤直徑 x,縱軸是預測標簽 y^,0 表示良性(no),1 表示惡性(yes)。
-
藍線和綠線表示模型輸出函數 fw,b(x)=wx+b。
-
當 fw,b(x)≥0.5 時,預測 y^=1;小于 0.5 時,預測 y^=0。
-
圖中藍圈表示實際為良性(0),紅叉為惡性(1)。
-
藍色豎線是“決策邊界”(decision boundary),左邊預測為0,右邊為1。
-
圖中有些樣本被錯誤分類(例如紅叉落在藍線左邊被預測為良性),屬于“misclassified”。
三、邏輯回歸的Sigmoid函數與分類閾值
-
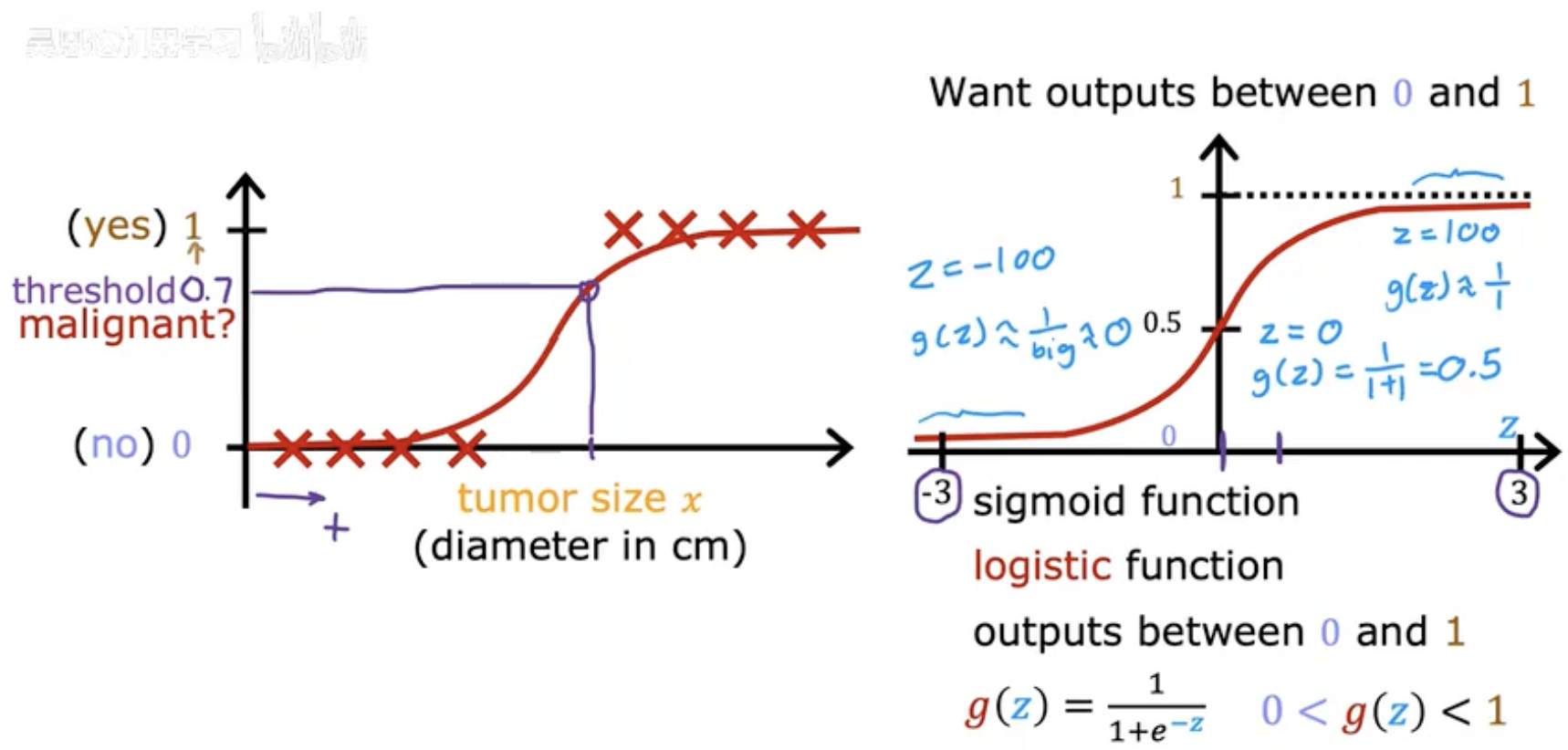
閾值(Threshold):圖中以“腫瘤是否惡性”為例,設定閾值為?0.7(若預測概率 ≥0.7 則判定為“惡性”(yes/1))。
-
輸入特征:腫瘤直徑(x,單位 cm)作為模型的輸入變量。
-
Sigmoid 函數:
-
核心公式:將任意實數 z 映射到?(0,1)?區間。
-
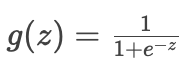
-
示例輸出:
-
z=?100 時,g(z)≈0(接近 0)。
-
z=0 時,g(z)=0.5。
-
-
四、邏輯回歸模型
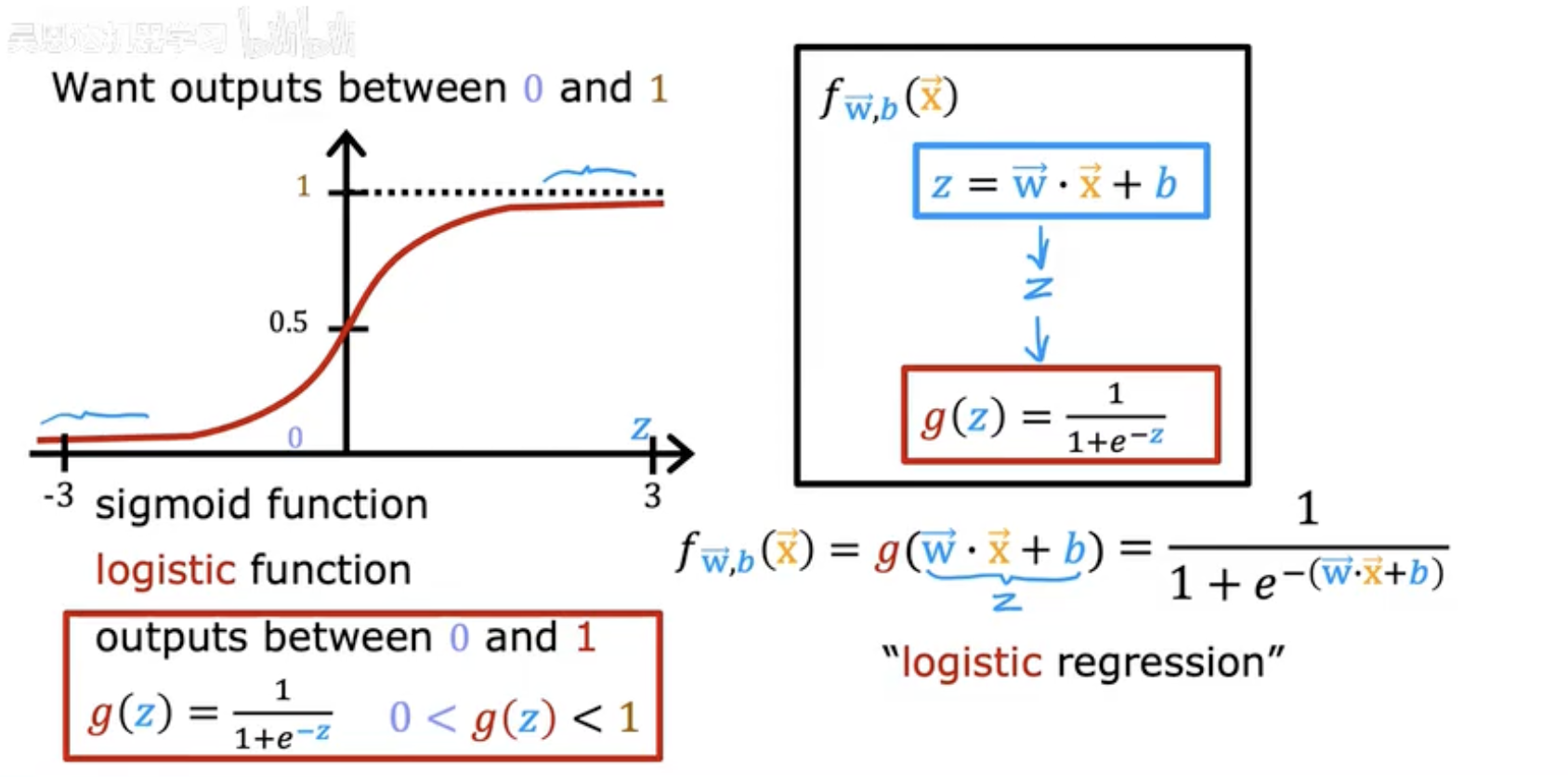
邏輯回歸模型:
-
輸入:特征向量?x?和參數?w?、偏置 b。
-
線性部分:z=w??x?+b。
-
最終輸出:
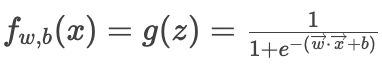
邏輯回歸輸出

-
邏輯回歸輸出解釋:
-
模型公式:,輸出表示樣本屬于類別?1?的概率。
-
示例:若 fw,b(x?)=0.7,表示有?70%?的概率 y=1y=1(如腫瘤為惡性)。
-
-
概率定義:
-
fw,b(x?)=P(y=1∣x;w,b):給定輸入 x 和參數 w,b,y=1 的條件概率。
-
兩類概率之和為 1:P(y=0)+P(y=1)=1。
-
-----------------------------------------------------------------------------------------------
這是我在我的網站中截取的文章,有更多的文章歡迎來訪問我自己的博客網站rn.berlinlian.cn,這里還有很多有關計算機的知識,歡迎進行留言或者來我的網站進行留言!!!
-----------------------------------------------------------------------------------------------


)
















