---

一、AVL樹的概念

• AVL樹是最先發明的?平衡?叉查找樹，AVL是?顆空樹，或者具備下列性質的?叉搜索樹：它的左右?樹都是AVL樹，且左右?樹的?度差的絕對值不超過1。AVL樹是?顆?度平衡搜索?叉樹，通過控制?度差去控制平衡。
• AVL樹得名于它的發明者G. M. Adelson-Velsky和E. M. Landis是兩個前蘇聯的科學家，他們在1962年的論?《An algorithm for the organization of information》中發表了它。
• AVL樹實現這?我們引??個平衡因?(balance factor)的概念，每個結點都有?個平衡因?，任何結點的平衡因?等于右?樹的?度減去左?樹的?度，(也可以左減右)也就是說任何結點的平衡因?等于0/1/-1，AVL樹并不是必須要平衡因?，但是有了平衡因?可以更?便我們去進?觀察和控制樹是否平衡，就像?個?向標?樣。
• 思考?下為什么AVL樹是?度平衡搜索?叉樹，要求?度差不超過1，?不是?度差是0呢？0不是更好的平衡嗎？畫畫圖分析我們發現，不是不想這樣設計，?是有些情況是做不到?度差是0的。?如?棵樹是2個結點，4個結點等情況下，?度差最好就是1，?法做到?度差是0。
• AVL樹整體結點數量和分布和完全?叉樹類似，?度可以控制在 logN，那么增刪查改的效率也可以控制在 O(logN)，相??叉搜索樹有了本質的提升。

二、AVL樹的實現

AVL樹的結構

template<class K, class V>
struct AVLTreeNode
{// 需要parent指針，后續更新平衡因?可以看到pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public://...
private:Node* _root = nullptr;
};

結點的成員變量這一塊我們不再分別定義key和value，而是用pair包起來，和map保持一致，方便后續模擬實現myset和mymap。相比以前多了一個指向parent的指針，后面的平衡旋轉操作會用到。還多了一個平衡因子_bf。
至于AVL樹的定義基本和之前的二叉搜索樹一樣。

AVL樹的插?

AVL樹插??個值的?概過程

1. 插入：插??個值按?叉搜索樹規則進?插?。
2. 更新平衡因?：新增結點以后，只會影響該結點祖先結點的?度，也就是可能會影響部分祖先結點的平衡因?，所以更新從新增結點->根結點路徑上的平衡因?，實際中最壞情況下要更新到根，有些情況更新到中間就可以停?了，具體情況我們下?再詳細分析。

更新平衡因?過程中沒有出現不平衡，則插?結束。
更新平衡因?過程中出現不平衡，對不平衡?樹旋轉，旋轉后調平衡的同時，本質降低了?樹的?度，不會再影響上?層，所以插?結束。

平衡因?更新

更新原則

• 平衡因? = 右?樹?度-左?樹?度。
• 只有?樹?度變化才會影響當前結點平衡因?。
• 插?結點，會增加當前結點parent的子樹?度，如果新增結點在parent的右?樹，parent的平衡因?++，新增結點在parent的左?樹，parent平衡因?–。
• parent所在?樹的?度是否變化決定了是否會繼續往上更新,判斷?度是否變化需要看下面介紹的更新停止條件。

更新停?條件

• 更新后parent的平衡因?等于0，說明更新中parent的平衡因?變化為-1->0 或者 1->0，說明更新前parent?樹?邊??邊低，新增的結點插?在低的那邊，插?后parent所在的?樹?度不變，不會影響parent的?親結點的平衡因?，更新結束。

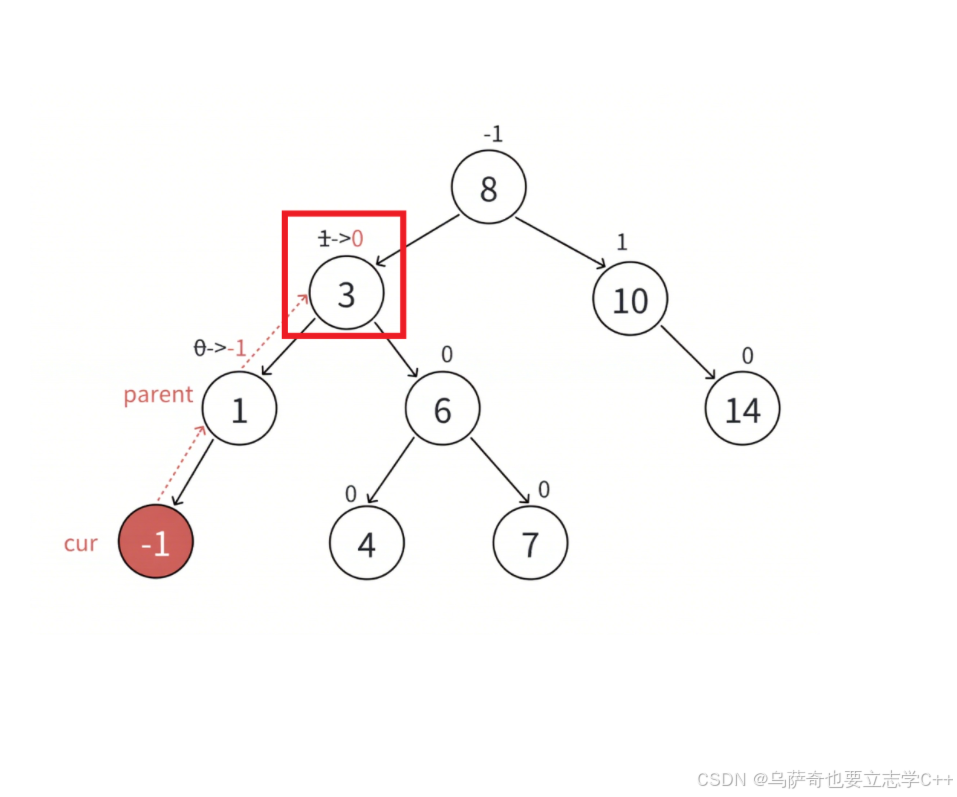
• 更新后parent的平衡因?等于1 或 -1，更新前更新中parent的平衡因?變化為0->1 或者 0->-1，說明更新前parent?樹兩邊?樣?，新增的插?結點后，parent所在的?樹?邊??邊低，parent所在的?樹符合平衡要求，但是?度增加了1，會影響parent的?親結點的平衡因?，所以要繼續向上更新。

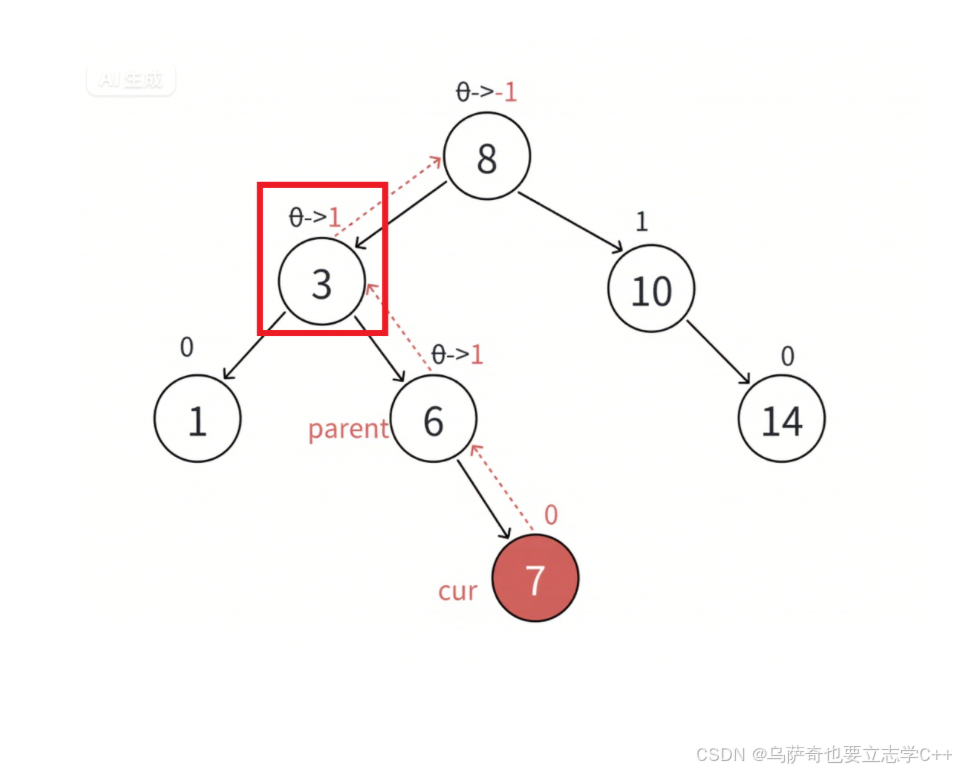
• 更新后parent的平衡因?等于2 或 -2，更新前更新中parent的平衡因?變化為1->2 或者 -1->-2，說明更新前parent?樹?邊??邊低，新增的插?結點在?的那邊，parent所在的?樹?的那邊更?了，破壞了平衡，parent所在的?樹不符合平衡要求，需要旋轉處理，旋轉的?標有兩個：1、把parent?樹旋轉平衡。2、降低parent?樹的?度，恢復到插?結點以前的?度。所以旋轉后也不需要繼續往上更新，更新停止。

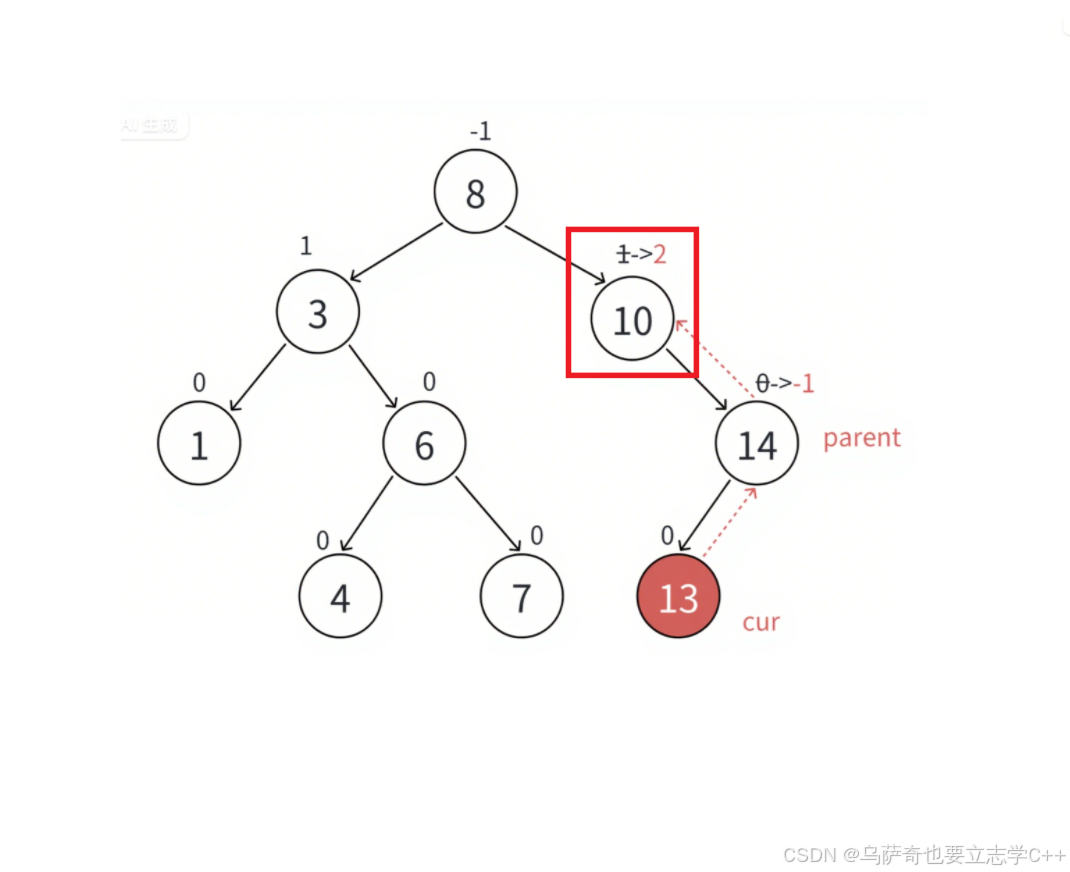
• 不斷更新，更新到根，根的平衡因?是1或-1也停?更新。

插入結點及更新平衡因子的代碼實現

插入操作和之前二叉搜索樹的邏輯相同，重點是這里更新平衡因子的代碼實現。 我們前面介紹過了更新平衡因子有三種可能(0, 1-1, 2-2)，但是我們在代碼里最好不要就只分三種情況討論，因為這三種情況是建立在前面代碼邏輯都正常的情況下，但是代碼是有可能出錯的，所以我們需要在代碼里再多寫一個出現錯誤的情況，如果走到這種情況了那么程序一定出現了問題，我們可以assert或者拋異常。
更行結束標志也有三種，一種是更新到根節點，parent指向nullptr，停止更新。一種是parent平衡因子更新到0，停止更新。還有一種是parent平衡因子更新到2或者-2,不平衡了需要旋轉，旋轉完后因為高度復原了所以停止更新。

bool Insert(const pair<K, V>& kv)
{//單純插入if (_root == nullptr){_root = new Node(kv);return true;}else{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first) {parent = cur;cur = cur->_left;}else if(cur->_kv.first < _kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = Node(kv);if (parent->_kv.first > kv.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;}//更新平衡因子while (parent) //若更新到根結點，更新結束---1{if (parent->_left == cur)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0){//更新結束---2break;}else if (parent->_bf == 1 || parent->_bf == -1){//繼續向上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//不平衡了，旋轉處理//旋轉完后，更新結束---3break;}else{//代碼出錯assert(false);}}return true;

旋轉

旋轉的原則

1、旋轉后保持搜索樹的規則
2. 讓旋轉的樹從不滿?變平衡，其次降低旋轉樹的?度。
3. 旋轉總共分為四種，左單旋/右單旋/左右雙旋/右左雙旋。
說明：下?的圖中，有些結點我們給的是具體值，如10和5等結點，這?是為了?便講解，實際中是什么值都可以，只要??關系符合搜索樹的性質即可。

右單旋

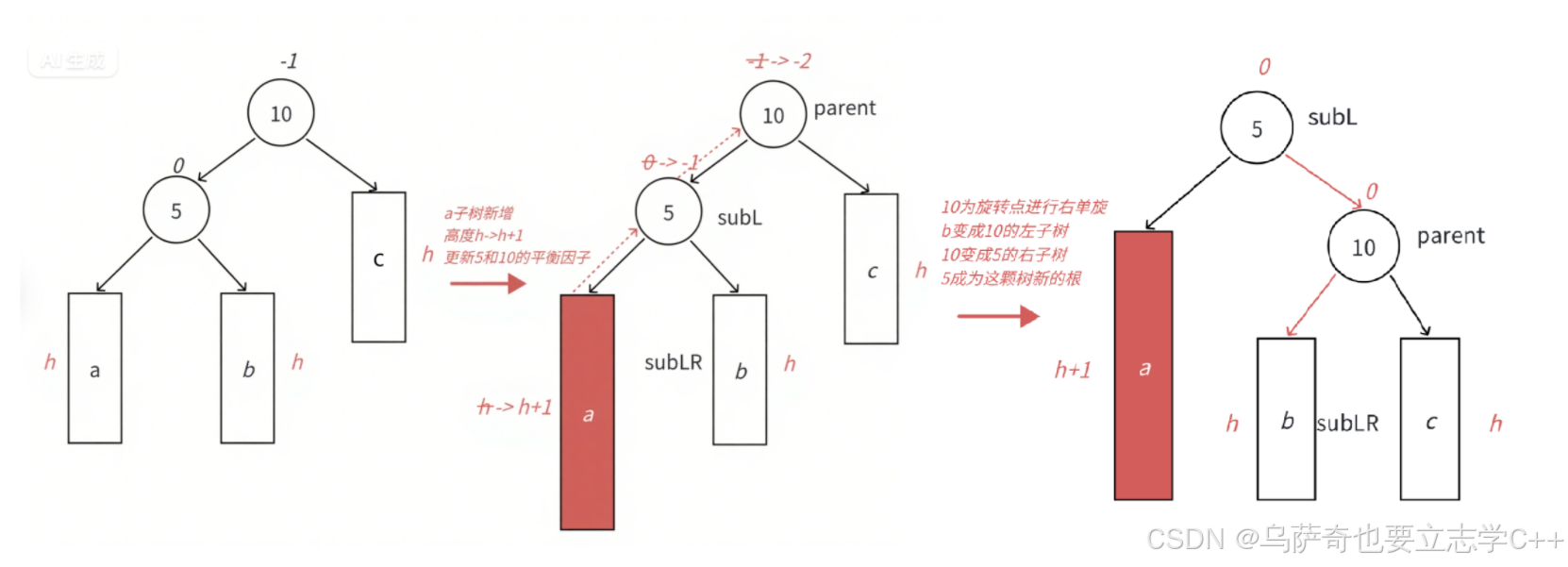
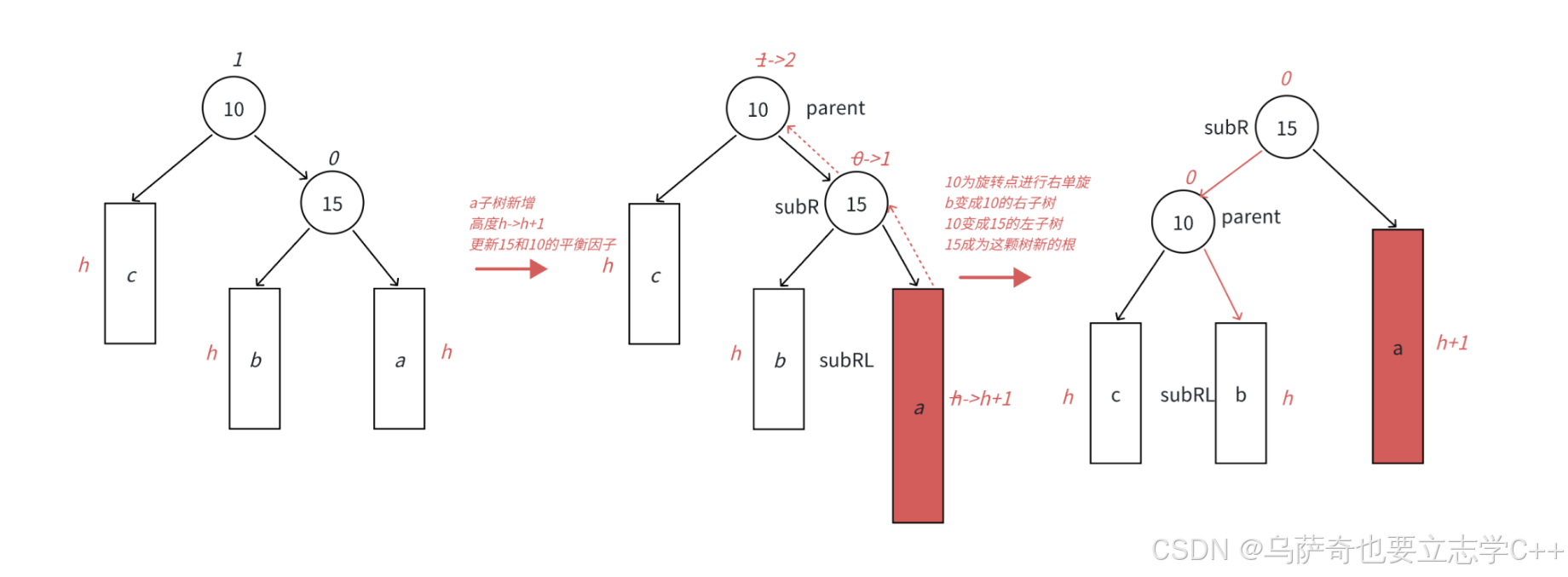
• 圖中展?的是10為根的樹，有a/b/c三棵抽象為?度h的?樹(h>=0)，a/b/c均符合AVL樹的要求。10可能是整棵樹的根，也可能是?個整棵樹中局部的?樹的根。這?a/b/c是?度為h的?樹，是?種概括抽象表?，他代表了所有右單旋的場景，實際右單旋形態有很多種。
• 在a?樹中插??個新結點，導致a?樹的?度從h變成h+1，不斷向上更新平衡因?，導致10的平衡因?從-1變成-2，10為根的樹左右?度差超過1，違反平衡規則。10為根的樹左邊太?了，需要往右邊旋轉，控制兩棵樹的平衡。
• 旋轉核?步驟，因為5 < b?樹的值 < 10，將b變成10的左?樹，10變成5的右?樹，5變成這棵樹新的根，符合搜索樹的規則，控制了平衡，同時這棵的?度恢復到了插?之前的h+2，符合旋轉原則。如果插?之前10是整棵樹的?個局部?樹，旋轉后局部?樹的高度恢復到插入之前，不會再影響上?層，插?結束。
  這里要把a打包看成一個整體，如果插入a也會引起旋轉那么a旋轉的步驟也和我們這里討論的一樣，所以這里我們只是講的是一個旋轉的模板，不管是a子樹里面的旋轉還是在10上面的樹的旋轉都適用。(如果10不是根節點的話)

右單旋代碼實現

一、首先把parent->_left = subLR, subL->_right = parent,這兩個調整孩子的步驟很簡單。
二、但是我們要記住AVL樹是三叉鏈，它的每個結點還有一個指向parent的指針，所以還需要調整subLR、parent、subL的_parent指針，調整_parent比較復雜。

• subLR->_parent = parent： 這里要注意subLR是可能為空的，所以需要判斷一下，為空就無需調整subLR的_parent。
• parent->_parent = subL： 這里沒有什么問題。
• subL->_parent 這里要分兩種情況討論，一種是當parent是根節點，那么需要把_root給給subL,subL->_parent = nullptr。一種是parent不是根節點，那么parent只是其中一顆子樹的根節點，所以需要維護我們在旋轉子樹與整個樹的關系,需要把subL->parent指向parent->parent,然后把parent->parent的_left或者_right指向subL，具體細節看下面代碼的注釋。

三、最后調整平衡因子，旋轉過程只有parent和subL的平衡因子會改變，而且都是變為0。

void RotateR(Node* parent)
{//調整兩個結點的孩子指針Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;subL->_right = parent;//調整三個結點的父親指針if (subLR) // 結點1subLR->_parent = parent;//提前保存一下parent->_parentNode* parentParent = parent->_parent;parent->_parent = subL; // 結點2//subL的_parent分三種情況if (parent == _root){//parent是根節點_root = subL;subL->_parent = nullptr;}else{subL->_parent = parentParent;if (parent == parentParent->_left){parentParent->_left = subL;}else{parentParent->_right = subL; // 結點3}}//調整平衡因子subL->_bf = parent->_bf = 0;
}

左單旋

左單旋和右單旋邏輯上基本一致，小編這里就不細講了。

左單旋代碼實現

void RotateL(Node* parent)
{//調整兩個結點的孩子指針Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;//調整三個結點的父親指針if (subRL) // 結點1subRL->_parent = parent;//提前保存一下parent->_parentNode* parentParent = parent->_parent;parent->_parent = subR; // 結點2//subR的parent分三種情況if (parent == _root){//parent是根節點_root = subR;subR->_parent = nullptr;}else{subR->_parent = parentParent;if (parent == parentParent->_left){parentParent->_left = subR;}else{parentParent->_right = subR; // 結點3}}//調整平衡因子subR->_bf = parent->_bf = 0;
}

左右雙旋

通過下面兩幅圖可以看到，左邊?時，如果插?位置不是在a?樹，?是插?在b?樹，b?樹?度從h變成h+1，引發旋轉，右單旋?法解決問題，右單旋后，我們的樹依舊不平衡。右單旋解決的純粹的左邊?，但是插?在b?樹中，10為跟的?樹不再是單純的左邊?，對于10是左邊?，但是對于5是右邊?，需要?兩次旋轉才能解決。以5為旋轉點進??個左單旋，(把一開始根的左邊小的右邊小調整成一邊小，這里被調整后都是左邊小)以10為旋轉點進??個右單旋，這棵樹就平衡了。(旋轉前是一邊小再單旋就可以平衡)

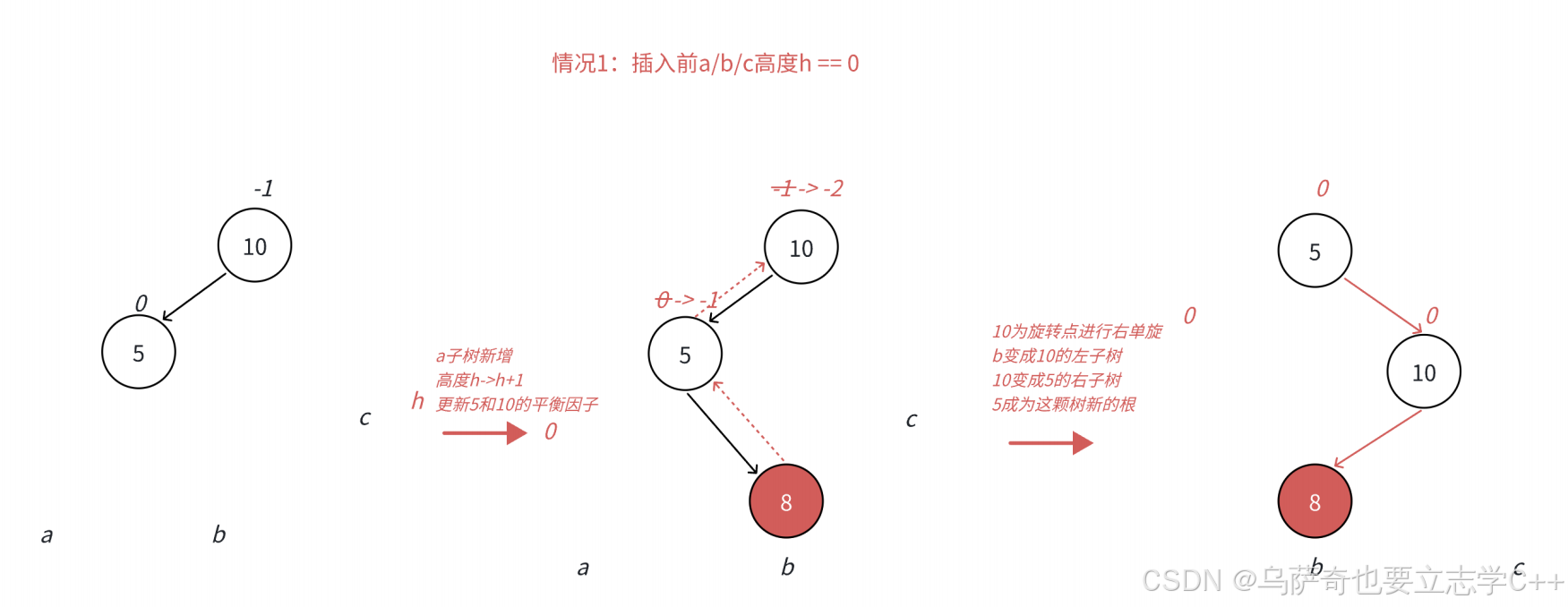
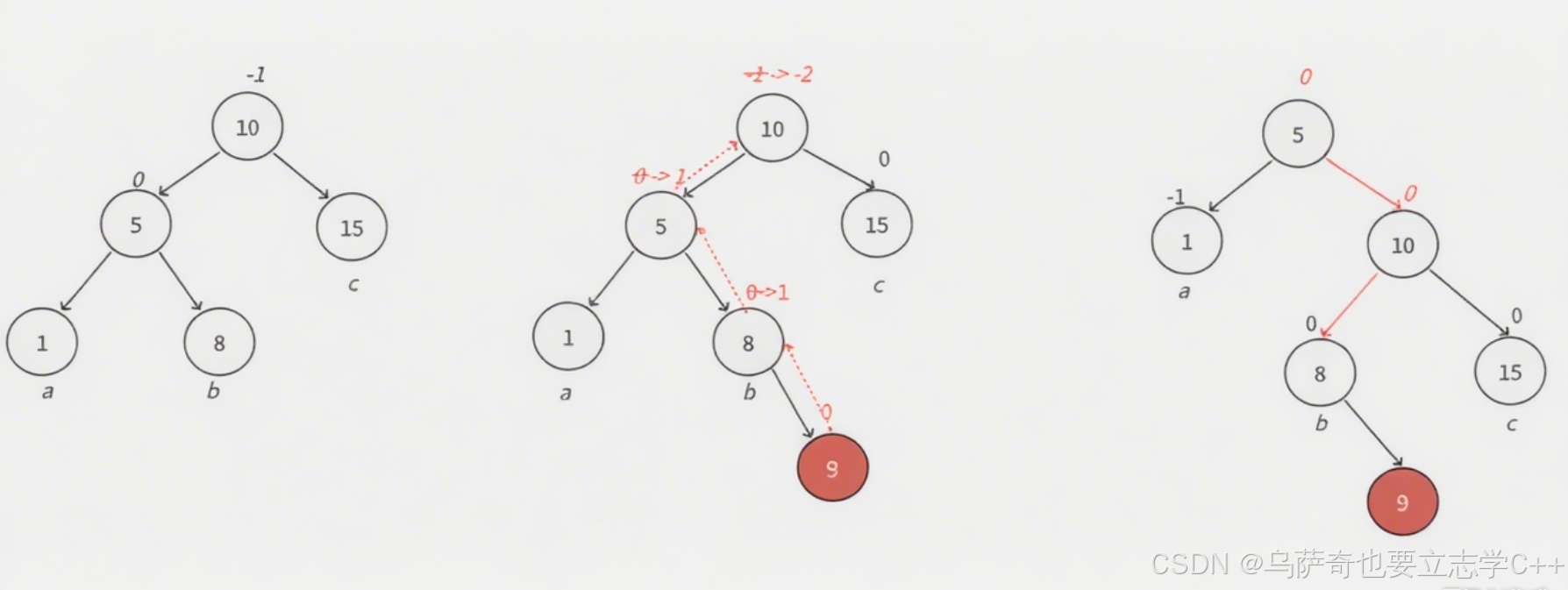
以5為旋轉點進??個左單旋，以10為旋轉點進??個右單旋，這棵樹這棵樹就平衡了。

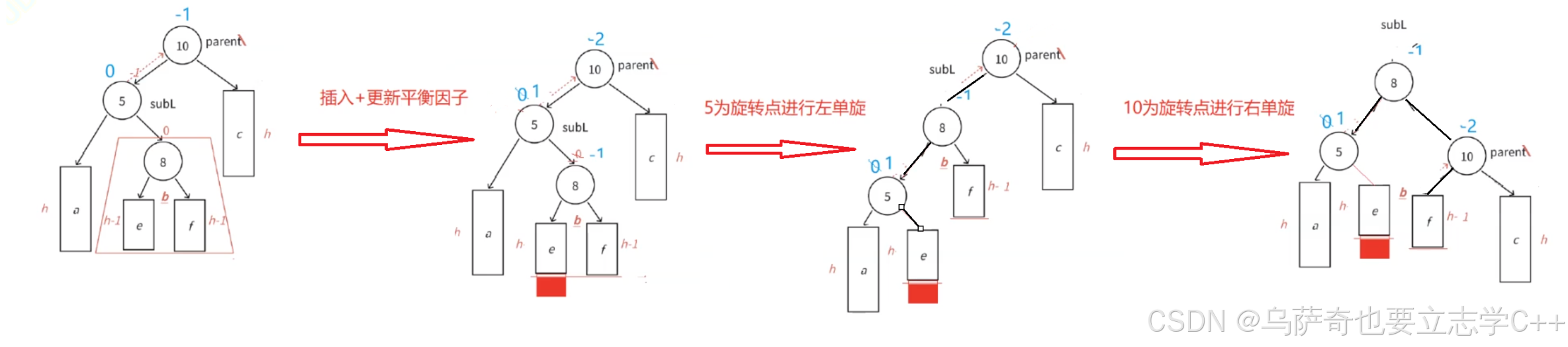
實際上左右雙旋是可以一步到位的，相當于把subLR的左邊分給了subL的右邊，subLR的右邊分給了parent的左邊,最后把subLR推上去做根，我們看下面這幅圖：

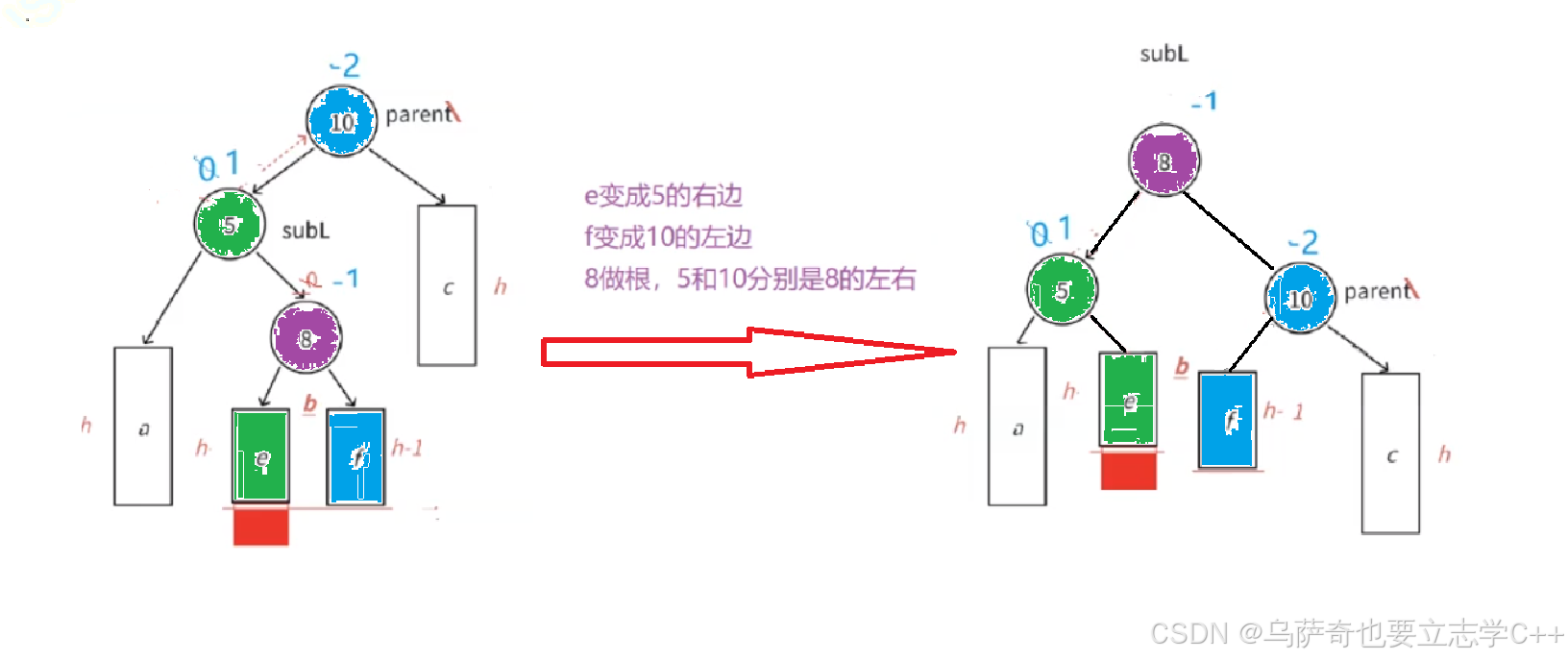
但是左右雙旋體現在代碼上還是一步一步來，因為可以復用單旋的代碼，更爽一點。

平衡因子的更新：
左右雙旋的旋轉過程如上所示，只有一種情況，但是三個結點平衡因子的更新有三種情況，分別是將結點插入到b子樹的e子樹(情況一)、b子樹的f子樹(情況二)、b子樹本身為空(情況三)，插入的結點本身就成了b子樹。插入時的前兩種情況旋轉結束后體現在subL右子樹的高度和parent左子樹的高度，最后一種情況表明旋轉只有三個結點參與，三個結點都沒有子樹。
最后平衡因子的結果是subLR始終為0，情況一subL為0，parent為-1，情況二subL為-1，parent為0，情況三subL、parent都為0。
要判別平衡因子的更新是哪種情況就需要記錄插入后subLR的平衡因子，而且需要在兩次單旋之前把值記錄下來，因為單旋會把結點的平衡因子都置為0，(因為單旋是以只有一邊大的邏輯來旋轉和調整平衡因子的，所以左右雙旋復用單旋代碼后需要手動調整平衡因子)如果subLR的平衡因子為-1那么是情況1，為1那么是情況2，為0那么是情況3。

左右雙旋代碼實現

void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int tembf = subLR->_bf;RotateL(parent->_left);RotateR(parent);//更新平衡因子subLR->_bf = 0;if (tembf == -1)     //情況一{subL->_bf = 0;parent->_bf = 1;}else if(tembf == 1)  //情況二{subL->_bf = -1;parent->_bf = 0;}else if(tembf == 0)  //情況三{subL->_bf = subLR->_bf = 0;}else{assert(false);}
}

右左雙旋代碼實現

void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int tembf = subRL->_bf;RotateR(subR);RotateL(parent);//更新平衡因子subRL->_bf = 0;if (tembf == -1)      //情況一{subR->_bf = 1;parent->_bf = 0;}else if(tembf == 1)   //情況二{subR->_bf = 0;parent->_bf = -1;}else if (tembf == 0)  //情況三{subR->_bf = subRL->_bf = 0;}else{assert(false);}
}

判斷旋轉

if (parent->_bf == -2 && cur->_bf == -1)    //右單旋
{RotateR(parent);
}
else if (parent->_bf == 2 && cur->_bf == 1) //左單旋
{RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1) //左右雙旋(平衡因子異號)
{RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1) //右左雙旋
{RotateRL(parent);
}

我們可以總結發現，單旋時兩個結點的平衡因子同號，雙旋時兩個結點的平衡因子異號。

中序遍歷

void InOrder()
{_InOrder(_root);cout << endl;
}void _InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);
}

平衡檢測(求高度)

我們實現的AVL樹是否合格，就是檢查每一個結點的平衡因子是否平衡，但是不能只檢查平衡因子，因為平衡因子也可能出問題，所以需要遞歸求出每一個結點的平衡因子是否符合要求，然后再拿算的平衡因子和結點內部的平衡因子比較。方法就是通過遞歸求當前結點左右子樹的高度，然后求當前結點左右?樹?度差進?反向驗證。
（代碼中的abs 是 C++ 標準庫中的一個函數，用于計算整數的絕對值（即去掉符號，只保留數值大小）

int Height()
{return _Height(_root);
}bool IsBalanceTree()
{return _IsBalanceTree(_root);
} int _Height(Node* root)
{if (root == nullptr)return 0;int LHeight = _Height(root->_left);int RHeight = _Height(root->_right);return 1 + (LHeight > RHeight ? LHeight : RHeight);
}bool _IsBalanceTree(Node* root)
{if (root == nullptr)return true;   //空樹也是AVL樹int diff = _Height(root->_right) - _Height(root->_left);if (abs(diff) >= 2){cout << "高度差異常" << endl;return false;}else if (diff != root->_bf){cout << "平衡因子異常" << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}

查找

bool Find(const K& x)
{Node* cur = _root;while (cur){if (cur->_kv.first == x)return true;else if (cur->_kv.first > x)cur = cur->_left;elsecur = cur->_right;}return false;
}

Size(求結點個數)

int Size()
{return _Sise(_root);
}int _Sise(Node* _root)
{if (_root == nullptr)return 0;return 1 + _Sise(_root->_left) + _Sise(_root->_right);
}

三、源碼

AVLTree.h：

#pragma once
using namespace std;
#include <iostream>
#include <assert.h>
#include <vector>template<class K, class V>
struct AVLTreeNode
{// 需要parent指針，后續更新平衡因?可以看到pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){//單純插入if (_root == nullptr){_root = new Node(kv);return true;}Node * parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first) //判斷cur插在parent的那邊parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;//更新平衡因子while (parent) //若更新到根結點，更新結束---1{if (parent->_left == cur)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0){//更新結束---2break;}else if (parent->_bf == 1 || parent->_bf == -1){//繼續向上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//不平衡了，旋轉處理if (parent->_bf == -2 && cur->_bf == -1)    //右單旋{RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1) //左單旋{RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1) //左右雙旋(平衡因子異號){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1) //右左雙旋{RotateRL(parent);}//旋轉完后，更新結束---3break;}else{//代碼出錯assert(false);}}return true; }void InOrder(){_InOrder(_root);cout << endl;}int Height(){return _Height(_root);}bool IsBalanceTree(){return _IsBalanceTree(_root);}  bool Find(const K& x){Node* cur = _root;while (cur){if (cur->_kv.first == x)return true;else if (cur->_kv.first > x)cur = cur->_left;elsecur = cur->_right;}return false;}int _Height(Node* root){if (root == nullptr)return 0;int LHeight = _Height(root->_left);int RHeight = _Height(root->_right);return 1 + (LHeight > RHeight ? LHeight : RHeight);}bool _IsBalanceTree(Node* root){if (root == nullptr)return true;   //空樹也是AVL樹int diff = _Height(root->_right) - _Height(root->_left);if (abs(diff) >= 2){cout << "高度差異常" << endl;return false;}else if (diff != root->_bf){cout << "平衡因子異常" << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}int Size(){return _Sise(_root);}int _Sise(Node* _root){if (_root == nullptr)return 0;return 1 + _Sise(_root->_left) + _Sise(_root->_right);}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}void RotateR(Node* parent){//調整兩個結點的孩子指針Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;subL->_right = parent;//調整三個結點的父親指針if (subLR) // 結點1subLR->_parent = parent;//提前保存一下parent->_parentNode* parentParent = parent->_parent;parent->_parent = subL; // 結點2//subL的_parent分三種情況if (parent == _root){//parent是根節點_root = subL;subL->_parent = nullptr;}else{subL->_parent = parentParent;if (parent == parentParent->_left){parentParent->_left = subL;}else{parentParent->_right = subL; // 結點3}}//調整平衡因子subL->_bf = parent->_bf = 0;}void RotateL(Node* parent){//調整兩個結點的孩子指針Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent;//調整三個結點的父親指針if (subRL) // 結點1subRL->_parent = parent;//提前保存一下parent->_parentNode* parentParent = parent->_parent;parent->_parent = subR; // 結點2//subR的parent分三種情況if (parent == _root){//parent是根節點_root = subR;subR->_parent = nullptr;}else{subR->_parent = parentParent;if (parent == parentParent->_left){parentParent->_left = subR;}else{parentParent->_right = subR; // 結點3}}//調整平衡因子subR->_bf = parent->_bf = 0;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int tembf = subLR->_bf;RotateL(parent->_left);RotateR(parent);//更新平衡因子subLR->_bf = 0;if (tembf == -1)     //情況一{subL->_bf = 0;parent->_bf = 1;}else if(tembf == 1)  //情況二{subL->_bf = -1;parent->_bf = 0;}else if(tembf == 0)  //情況三{subL->_bf = subLR->_bf = 0;}else{assert(false);}}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int tembf = subRL->_bf;RotateR(subR);RotateL(parent);//更新平衡因子subRL->_bf = 0;if (tembf == -1)      //情況一{subR->_bf = 1;parent->_bf = 0;}else if(tembf == 1)   //情況二{subR->_bf = 0;parent->_bf = -1;}else if (tembf == 0)  //情況三{subR->_bf = subRL->_bf = 0;}else{assert(false);}}private:Node* _root = nullptr;
};

test.c:

#include "AVLTree.h"void TestAVLTree1()
{AVLTree<int, int> t;// 常規的測試?例int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };// 特殊的帶有雙旋場景的測試?例//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){t.Insert({ e, e });}t.InOrder();cout << t.IsBalanceTree() << endl;
}// 插??堆隨機值，測試平衡，順便測試?下?度和性能等
void TestAVLTree2()
{const int N = 100000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);}size_t begin2 = clock();AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();cout << "Insert:" << end2 - begin2 << endl;cout << t.IsBalanceTree() << endl;cout << "Height:" << t.Height() << endl;cout << "Size:" << t.Size() << endl;size_t begin1 = clock();// 確定在的值for (auto e : v){t.Find(e);}// 隨機值//for (size_t i = 0; i < N; i++)//{//	t.Find((rand() + i));//}size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;
}int main()
{//TestAVLTree1();TestAVLTree2();return 0;
}

以上就是小編分享的全部內容了，如果覺得不錯還請留下免費的關注和收藏
如果有建議歡迎通過評論區或私信留言，感謝您的大力支持。
一鍵三連好運連連哦~~