最短路徑的典型用途：

交通網絡的問題——從甲地到乙地之間是否有公路連通？

在有多條通路的情況下，哪一條路最短？

交通網絡用有向網來表示：頂點——表示地點，弧——表示兩個地點有路連通，弧上的權值——表示兩地點之間的距離、交通費或途中所花費的時間等。

如何能夠使一個地點到另一個地點的運輸時間最短或運費最省？這就是一個求兩個地點間的最短路徑問題。

問題抽象：

在有向網中A點（源點）到達B點（終點）的多條路徑中，尋找一條各邊權值之和最小的路徑，即最短路徑。

最短路徑與最小生成樹不同，路徑上不一定包含n個頂點，也不一定包含n - 1條邊。

第一類問題是求兩點間的最短路徑：下圖是兩點間的距離，求最短路徑，比如是從V1到V7，我們將所有可能的路徑一一羅列并求權值之和，比較大小

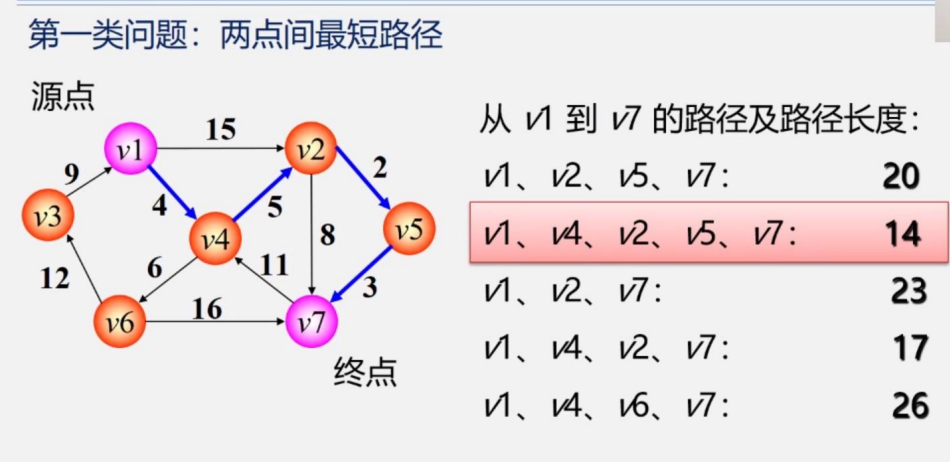
第二類問題是求某源點到其他個點的最短路徑：此時源點是任取的，看你想要哪個作為起點

下圖中，比如由V0到V4的最短路徑，有兩條，一條是V0-V2-V3-V4=8+5+6=19，還有一條是V0直接到V4，權值是30，很明顯19更小，所有19填入表中，以此類推，不再贅述

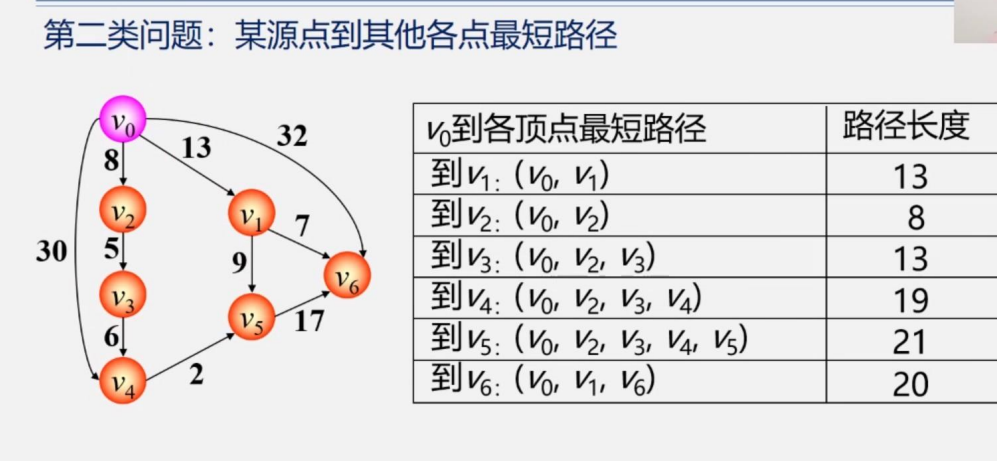
兩種常見的最短路徑問題：

一、單源最短路徑：用Dijkstra（迪杰斯特拉）算法

二、所有頂點間的最短路徑：用Floyd（弗洛伊徳）算法

接下來我們來分析迪杰斯特拉算法

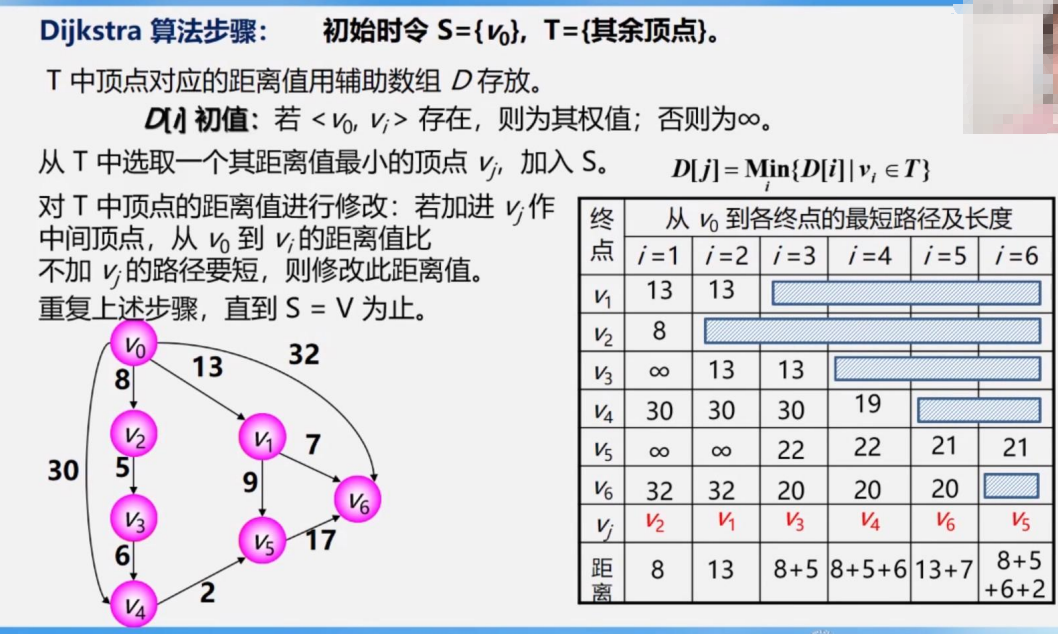
如下圖表，i=1所在的列，是指的V0到其他所有頂點的權值，如果沒有直達的邊（一條），記為∞

1.從VO到V1，權值為13，所以我們在V1所在行的第一個表格上填13，V0到V2權值為8，所以在V2所在行第一個表格填8，以此類推，V0到V4為30，V0到V6為32，其余填∞

2.找出填好的這一列（i=1所在的列）最小的權值，填到距離那行，也就是權值為8最小，對應的是V2，將V2填入Vj那一行，于是V2所在行劃去，因為我們已經找到到達V2的最小距離

3.接著，從V0和VO-V2出發，繼續尋找最短路徑，V0-V1依然不變是13，而V0-V2到V3，權值為8+5=13，除此之外無從V0/V2出發的路徑能到達V3，所以V3的值改為13，V4沒有V0-V2能直接到的邊（就是走一條邊就能到），所以依然是30不變，以此類推

4.我們發現，此時13是最小路徑，把第一個13（V1）放入距離和Vj中，劃去V1所在行，此后不再需要比較V1和V2的路徑

以此類推，不再贅述

弗洛依德 (Floyd) 算法思想：?

逐個頂點試探 ，從 Vi到 Vj 的所有可能存在的路徑中 ，選出一條長度最短的路徑

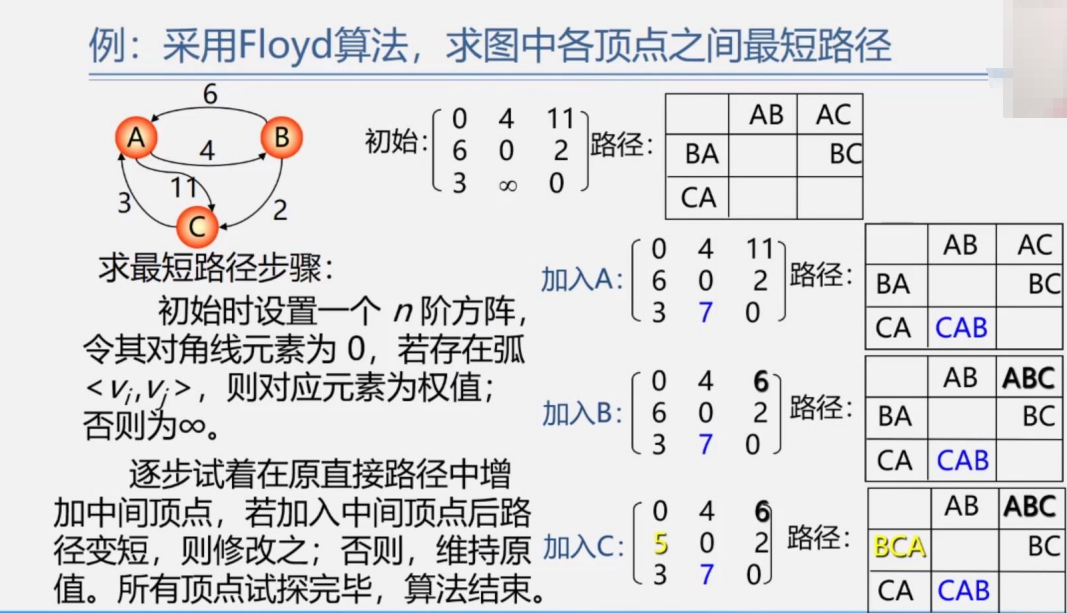
我們一 一分析一下這道題

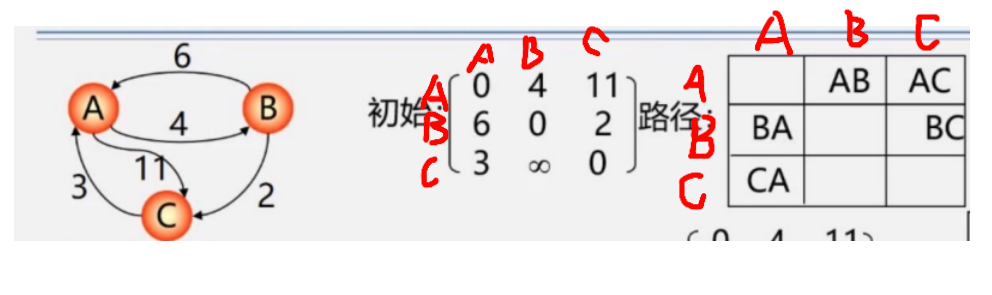
從A->B，權值是4，A->C是11，以此類推，主對角線均為0（因為A到A，B到B，C到C均無邊）

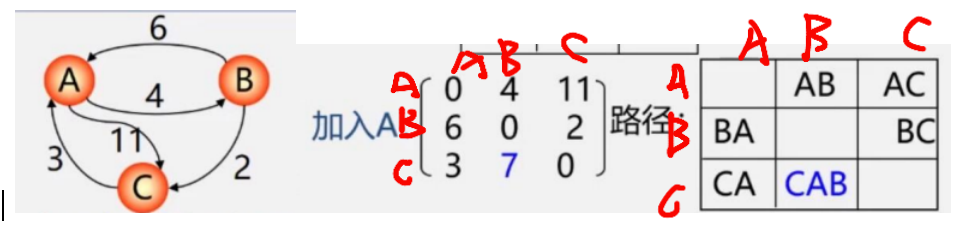
加入A的意思是，比如從B到C，那加入A就是B-A-C的路徑，是6+11=17>2，所以BC不動

分析C到B，加入A就是CAB=3+4=7<∞，所以改為7

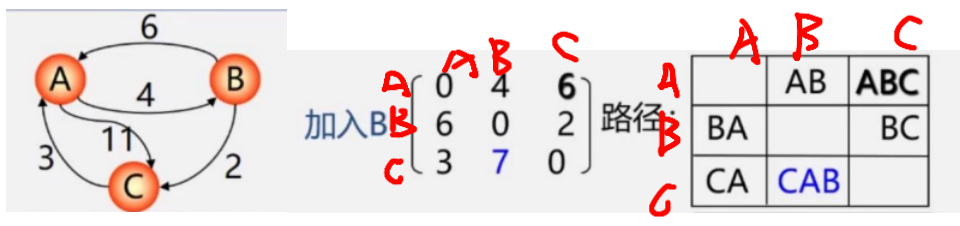
加入B，我們分析A到C，ABC=4+2=6<11，所以改為6

分析C到A，CBA，C沒有直接到B的，所以不必改

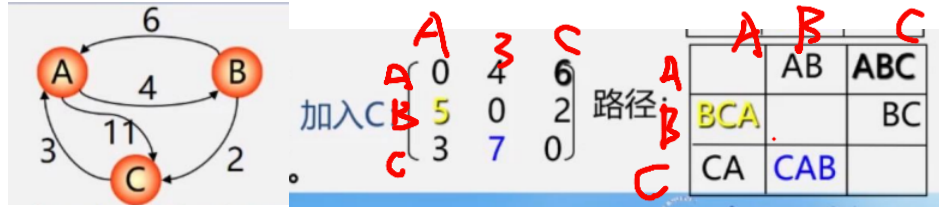
加入C，我們分析BA，B-C-A=2+3=5<6，所以改為5

總結：加入誰，誰所在的行先不變，對角線永遠是0