自動駕駛中的坐標系概念及相互間的轉換公式推導

在自動駕駛系統中，多個坐標系用于描述車輛、傳感器和環境的相對位置。這些坐標系之間的轉換是實現定位、感知和控制的關鍵。下面我將逐步解釋常見坐標系的概念，并推導相互轉換的公式。推導基于標準幾何變換和齊次坐標表示，確保公式正確可靠。

一、坐標系概念

在自動駕駛中，主要涉及以下坐標系：

1. 世界坐標系（World Coordinate System）：全局坐標系，固定在地球上（如基于GPS或地圖），原點通常為固定參考點（如起點）。用于描述車輛和環境在全局中的位置。
2. 車輛坐標系（Vehicle Coordinate System）：以車輛為中心，原點通常在車輛重心或后軸中心。$x$軸指向車輛前進方向，$y$軸指向左側，$z$軸向上。用于描述車輛自身狀態。
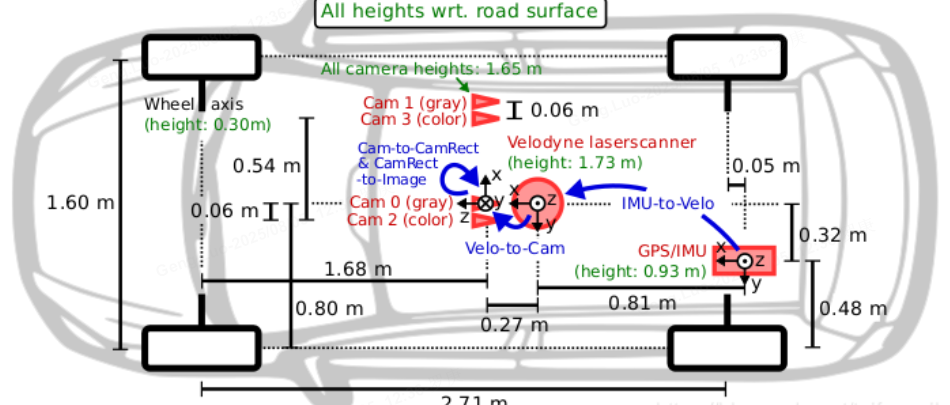
3. 傳感器坐標系（Sensor Coordinate System）：以傳感器（如激光雷達、攝像頭）為中心，原點在傳感器安裝點。每個傳感器有自己的坐標系，用于描述傳感器測量數據。
4. 相機坐標系（Camera Coordinate System）：針對攝像頭，原點在相機光心，$z$軸沿光軸方向，$x$軸和$y$軸平行于圖像平面。用于描述點在相機空間的位置。
5. 像素坐標系（Pixel Coordinate System）：針對圖像傳感器，原點在圖像左上角，$u$軸向右，$v$軸向下。用于描述像素位置。

這些坐標系相互關聯，需要通過旋轉和平移進行轉換。轉換通常使用齊次坐標（Homogeneous Coordinates）來表示，以簡化矩陣運算。齊次坐標形式為 $\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$。

二、坐標系轉換公式推導

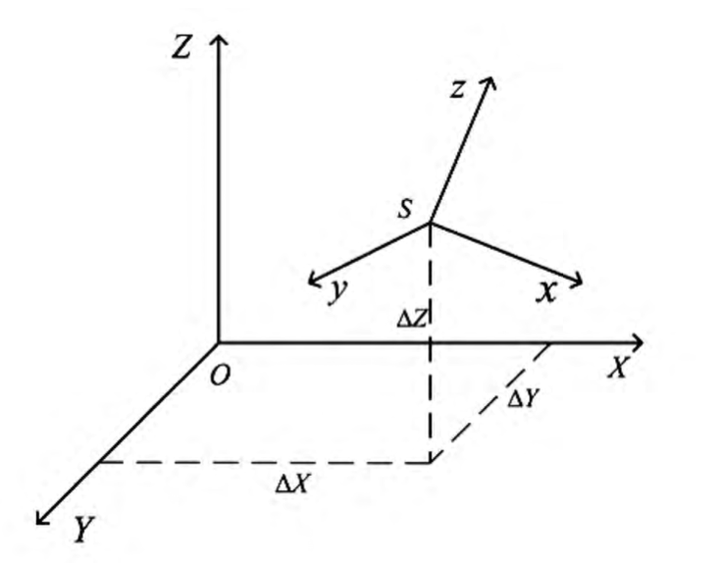
轉換公式推導基于歐幾里得變換，包括旋轉矩陣（Rotation Matrix）和平移向量（Translation Vector）。旋轉矩陣表示方向變化，平移向量表示位置偏移。推導從簡單到復雜，逐步構建完整轉換鏈。

步驟1: 世界坐標系到車輛坐標系的轉換

• 概念：車輛坐標系相對于世界坐標系的位置和方向變化，由車輛的位姿（位置和姿態）定義。
• 推導：
  • 設點 $P_w=\left[\begin{array}{c}{x}_w\\ y_w\\ z_w\end{array}\right]$ 在世界坐標系。
  • 設旋轉矩陣 $R_{wv}$（從世界到車輛）表示方向變化，平移向量 $t_{wv}=\left[\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]$ 表示車輛原點在世界坐標系中的位置。
  • 在車輛坐標系中，點 $P_v$ 的坐標為：
    $$P_v=R_{wv}(P_w?t_{wv})$$
  • 使用齊次坐標簡化：
    $$\left[\begin{array}{c}{P}_v\\ 1\end{array}\right]=\left[\begin{array}{cc}{R}_{wv}& ?R_{wv}{t}_{wv}\\ 0& 1\end{array}\right]\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$
  • 定義變換矩陣 $T_{wv}=\left[\begin{array}{cc}{R}_{wv}& ?R_{wv}{t}_{wv}\\ 0& 1\end{array}\right]$，則：
    $$\left[\begin{array}{c}{P}_v\\ 1\end{array}\right]=T_{wv}\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$
  • 其中，$R_{wv}$ 是正交矩陣，滿足 $R_{wv}{R}_{wv}^T=I$（單位矩陣），表示純旋轉。

步驟2: 車輛坐標系到傳感器坐標系的轉換

• 概念：傳感器（如激光雷達）安裝在車輛上，其坐標系相對于車輛坐標系有固定偏移。
• 推導：
  • 設點 $P_v=\left[\begin{array}{c}{x}_v\\ y_v\\ z_v\end{array}\right]$ 在車輛坐標系。
  • 設旋轉矩陣 $R_{vs}$（從車輛到傳感器）和平移向量 $t_{vs}=\left[\begin{array}{c}{t}_{sx}\\ t_{sy}\\ t_{sz}\end{array}\right]$（傳感器原點在車輛坐標系中的位置）。
  • 在傳感器坐標系中，點 $P_s$ 的坐標為：
    $$P_s=R_{vs}(P_v?t_{vs})$$
  • 齊次坐標形式：
    $$\left[\begin{array}{c}{P}_s\\ 1\end{array}\right]=\left[\begin{array}{cc}{R}_{vs}& ?R_{vs}{t}_{vs}\\ 0& 1\end{array}\right]\left[\begin{array}{c}{P}_v\\ 1\end{array}\right]$$
  • 定義變換矩陣 $T_{vs}=\left[\begin{array}{cc}{R}_{vs}& ?R_{vs}{t}_{vs}\\ 0& 1\end{array}\right]$，則：
    $$\left[\begin{array}{c}{P}_s\\ 1\end{array}\right]=T_{vs}\left[\begin{array}{c}{P}_v\\ 1\end{array}\right]$$
  • 結合步驟1，世界到傳感器的轉換：
    $$\left[\begin{array}{c}{P}_s\\ 1\end{array}\right]=T_{vs}{T}_{wv}\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$

步驟3: 相機坐標系到像素坐標系的轉換

• 概念：攝像頭將3D點投影到2D圖像平面，轉換涉及相機內參（焦距、光心）。
• 推導：
  • 設點 $P_c=\left[\begin{array}{c}{x}_c\\ y_c\\ z_c\end{array}\right]$ 在相機坐標系。
  • 使用針孔相機模型：點投影到圖像平面，坐標 $(x_p,y_p)$ 滿足：
    $$x_p=\frac{f_x{x}_c}{z_c},y_p=\frac{f_y{y}_c}{z_c}$$
    其中 $f_x$ 和 $f_y$ 是等效焦距（考慮像素縮放）。
  • 轉換到像素坐標系，考慮光心偏移 $(c_x,c_y)$：
    $$u=f_x\frac{x_c}{z_c}+c_x,v=f_y\frac{y_c}{z_c}+c_y$$
  • 寫成矩陣形式：
    $$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{z_c}\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_c\\ y_c\\ z_c\end{array}\right]$$
  • 定義相機內參矩陣 $K=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]$，則：
    $$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]\equiv K\left[\begin{array}{c}{x}_c/z_c\\ y_c/z_c\\ 1\end{array}\right]$$
    （其中 $\equiv$ 表示齊次坐標等價，需歸一化處理）。

完整轉換鏈示例：世界坐標系到像素坐標系

• 場景：給定世界坐標系中的點，如何得到其在圖像中的像素位置（如用于目標檢測）。
• 推導：
  • 結合所有步驟：世界坐標系 → 車輛坐標系 → 傳感器坐標系（相機） → 像素坐標系。
  • 設傳感器是相機，則從步驟2：$P_s=P_c$（相機坐標系）。
  • 轉換鏈：
    $$\left[\begin{array}{c}{P}_c\\ 1\end{array}\right]=T_{vs}{T}_{wv}\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$
    $$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{z_c}K\left[\begin{array}{cc}I& 0\end{array}\right]\left[\begin{array}{c}{P}_c\\ 1\end{array}\right]$$
    （其中 $\left[\begin{array}{cc}I& 0\end{array}\right]$ 提取 $P_c$ 的前三維）。
  • 完整公式：
    $$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\frac{1}{z_c}K\left[\begin{array}{cc}I& 0\end{array}\right]T_{vs}{T}_{wv}\left[\begin{array}{c}{P}_w\\ 1\end{array}\right]$$
  • 簡化：令 $z_c$ 是 $P_c$ 的 $z$ 分量，計算時需先求解 $P_c$。

三、關鍵注意事項

• 旋轉矩陣計算：旋轉矩陣通常由歐拉角或四元數推導。例如，繞 $z$ 軸旋轉 $\theta$ 角：
  $$R_z(\theta )=\left[\begin{array}{ccc}\cos \theta & ?\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right]$$
• 誤差處理：實際系統中，轉換參數（如 $R_{wv}$, $t_{wv}$）通過標定獲得，可能涉及優化算法（如最小二乘法）減少誤差。
• 應用：這些轉換用于傳感器融合（如融合攝像頭和激光雷達數據）、路徑規劃等。確保轉換鏈一致，避免累積誤差。

這個推導基于標準幾何原理，在自動駕駛系統中廣泛應用。如果您有具體場景（如特定傳感器類型），我可以進一步細化推導。