前言

又被卡在第二題了，當時腦子跟犯糊涂似的，B題越理越亂，導致比賽結束，還在想著題，徹夜難眠！

---

A.Submission is All You Need

Submission is All You Need
題目大意：

操作：

思路：只需要統計0的個數就行了，有多少個0就加上多少個1
由于mex的特性，以及操作時的特點，只要把0變成1就行，
代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define fi first
#define se second 
#define pii pair<ll,ll>
const ll N=1e6+10;
ll s[N];
ll sum[N];
void slove()
{ll n;cin>>n;ll f=0;for(ll i=1;i<=n;i++){cin>>s[i];sum[i]=s[i]+sum[i-1];if(s[i]==0)f++;}cout<<sum[n]+f<<endl;
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)slove();return 0;
}

B. Pathless

Pathless

思路;
對于這一題是有規律的
如果a1,a2,…,an的和sum
1.如果sum>s;
則一定不會滿足條件，這時只需要按原數組輸出就行
2.sum==s
這種是一定會滿足的直接輸出-1；
3.s>sum
如果s-sum=1，可以通過先0后2再1的順序輸出
這樣可以使得往返之后的額外增加的數，不管如何都不會湊成1
如果大于1,這一種不管如何排列，總會找到相鄰的數進行往返，以此來湊齊多出的數
因為相鄰數對的和可以通過線性組合覆蓋所有大于1的數
代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define fi first
#define se second 
#define pii pair<ll,ll>
const ll N=1e6+10;
ll s1[N];
void slove()
{ll n,s;cin>>n>>s;ll sum=0;ll a1=0,b1=0,c1=0;for(ll i=1;i<=n;i++){cin>>s1[i];if(s1[i]==0)a1++;else if(s1[i]==1)b1++;elsec1++;sum+=s1[i];}if(sum>s){for(ll i=1;i<=n;i++)cout<<s1[i]<<" ";cout<<endl;}else{if(sum==s){cout<<-1<<endl;}else{s=s-sum;if(s==1){for(ll i=1;i<=a1;i++)cout<<0<<" ";for(ll i=1;i<=c1;i++)cout<<2<<" ";for(ll i=1;i<=b1;i++)cout<<1<<" ";cout<<endl;return ;}cout<<-1<<endl;}}
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)slove();return 0;
}

C.Double Perspective

Double Perspective

其中主要的意思就是
f(s)代表的是在數軸上兩點之間距離之和
就比如（1，2）（2， 3）（3,4）其f（s）就是3；
而g（s）
則代表的是成環的長度，此時ai與bi是一條無向邊
就比如（1,2）（2,4）（1,4）此時成環，即g（s）=3；
了解完這些之后就是然后找到f（s）-g（s）的最大值
其實很簡單，只需要把成環的邊去掉，則剩下的集合就是最大的
代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
ll k;
ll s[N];
ll h[N];
void in()//初始化
{for(ll i=1;i<=2*k;i++){s[i]=i;h[i]=0;}
}
ll find(ll x)//查找根節點
{ll r=x;while(r!=s[r])r=s[r];ll i=x,j;while(i!=j){j=s[i];s[i]=r;i=j;}return r;
}
void mset(ll l,ll r)//合并
{l=find(l);r=find(r);if(l==r)return ;if(h[l]<h[r]){s[l]=r;}else{if(h[l]==h[r])h[r]++;s[r]=l;}return ;
}
void slove()
{cin>>k;in();vector<ll> p;for(ll i=1;i<=k;i++){ll l,r;cin>>l>>r;l=find(l);r=find(r);if(l!=r)//如果不成環，相當于把成環的跳過了{mset(l,r);p.push_back(i);}}cout<<p.size()<<endl;for(auto i:p)cout<<i<<" ";cout<<endl;
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)slove();return 0;
}

D.Stay or Mirror

Stay or Mirror

題目的意思就是尋找逆序對的，就是這個條件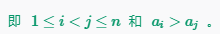
通過這個操作
能否使逆序對最小化。
注意：

當然這一題利用的貪心策略：
對于每個元素 p [i]，計算兩種選擇（保留原值或選擇 2n-p [i]）分別會產生的逆序數貢獻，然后選擇貢獻較小的那個
對于數組中的每個元素 p [i]，代碼計算兩個值：
l：在 p [i] 之前（j < i）且比 p [i] 大的元素數量
r：在 p [i] 之后（j > i）且比 p [i] 大的元素數量
為什么這樣計算？
當選擇保留 p [i] 時，它會與前面所有比它大的元素形成逆序對，貢獻為 L
當選擇 2n-p [i] 時，由于 2n-p [i] 的值較大（對于排列中的元素），它不會與前面的元素形成逆序對，而是會與后面比它小的元素形成逆序對。而后面比 p [i] 大的元素數量 R，恰好等于后面比 2n-p [i] 小的元素數量（因為 2n-p [i] 較大）
因此，對于每個元素，取 min (L, R) 作為它對總逆序數的最小貢獻，累加后得到最終結果。
代碼：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e4+10;
ll s[N];
void slove()
{ll n;cin>>n;for(ll i=1;i<=n;i++){cin>>s[i];}ll ans=0;for(ll i=1;i<=n;i++){ll l=0,r=0;for(ll j=1;j<=i;j++)//保留是s[i];if(s[j]>s[i])l++;for(ll j=i+1;j<=n;j++)//選擇2n-s[i];if(s[j]>s[i])r++;ans+=min(l,r);//取其貢獻最小的累加到答案}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)slove();return 0;
}