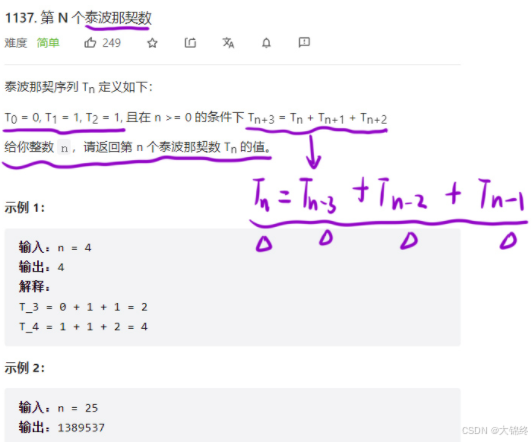
一. (1137.)第N個泰波那契數(力扣)
1.1動態規劃的算法流程
對于初學者來講學術上的概念晦澀難懂,將用通俗易懂的方式帶來感性的理解.
1.狀態表示
dp表(一維或二維數組)里面的值所表示的含義
從哪獲取?
1.題目要求,如本題
2.題目沒有明確說明的情況下+做題經驗的累積
3.分析問題的過程中,發現重復的子問題來概括
2.狀態轉移方程
就是dp表元素等于什么,是一種遞推關系式,本題已告知
3.初始化
要確保填dp表時不越界,對填表時越界的元素首先初始化
4.填表順序
為了填寫當前狀態的時候,所需要的狀態已經計算過了的順序,本題為從左向右
5.返回值
取決于題目要求+狀態表示,本題為第n個數的值
class Solution {
public:int tribonacci(int n) {//處理邊界情況if(n==0) return 0;if(n==1||n==2) return 1;vector<int> dp(n+1);dp[0]=0,dp[1]=1,dp[2]=1;for(int i=3;i<=n;i++){dp[i]=dp[i-1]+dp[i-2]+dp[i-3];}return dp[n];}
};
6.空間優化
只會在本系列和背包問題中出現并分析,為了降低空間復雜度,能將一個級別
分析本題:滾動數組法
常規做法通過創建一個dp表數組來計算并存儲結果,但是通過遞推關系式得知想得到當前數的值只需要知道前面三個元素的值即可,那么另外不需要的空間就相當于浪費,所以可以考慮用四個變量來記錄,每次更新后三個變量來進行下一次計算,如此循環往復
要注意更新變量的數據順序問題,避免被覆蓋
做法1:
class Solution {
public:int tribonacci(int n) {//處理邊界情況if(n==0) return 0;if(n==1||n==2) return 1;//優化int k=3;//初始計算次數,從第三次開始計算int a=0,b=1,c=1,d=0;while(k<=n)//判斷計算次數,返回條件{d=a+b+c;//更新變量a=b,b=c,c=d;k++;}return d;}
};做法2(不用控制計算次數):
class Solution {
public:int tribonacci(int n) {if(n == 0) return 0;if(n == 1 || n == 2) return 1;int a = 0, b = 1, c = 1, d = 0;for(int i = 3; i <= n; i++){d = a + b + c;a = b; b = c; c = d;}return d;}};
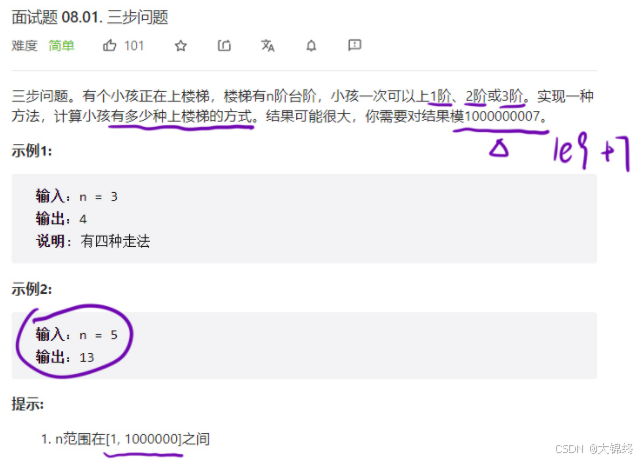
二. ?試題 08.01. 三步問題(力扣)
2.1算法原理
- 狀態表?
這道題可以根據「經驗 + 題?要求」直接定義出狀態表?:
dp[i] 表?:到達 i 位置時,?共有多少種?法。
- 狀態轉移?程
以 i 位置狀態的最近的?步,來分情況討論:
如果 dp[i] 表??孩上第 i 階樓梯的所有?式,那么它應該等于所有上?步的?式之和:(一次最多上三級臺階)
i. 上?步上?級臺階, dp[i] += dp[i - 1] ;
ii. 上?步上兩級臺階, dp[i] += dp[i - 2] ;
iii. 上?步上三級臺階, dp[i] += dp[i - 3] ;
綜上所述, dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] 。
需要注意的是,這道題?說,由于結果可能很?,需要對結果取模。在計算的時候,三個值全部加起來再取模,即 (dp[i - 1] + dp[i - 2] + dp[i - 3]) %MOD 是不可取的, n 取題?范圍內最?值時,?站會報錯 signed integer overflow 。
對于這類需要取模的問題,我們每計算?次(兩個數相加/乘等),都需要取?次模。否則,萬?發?了溢出,答案就錯了
- 初始化
從我們的遞推公式可以看出, dp[i] 在 i = 0, i = 1 以及 i = 2 的時候是沒有辦法進?推導的,因為 dp[-3] dp[-2] 或 dp[-1] 不是?個有效的數據。因此我們需要在填表之前,將 0,1, 2位置的值初始化。根據題意,, dp[0] = 1, dp[1] = 1, dp[2] = 2。
- 填表順序
爬臺階從下往上,對應數組從左往右,毫?疑問是「從左往右」。
- 返回值
應該返回 dp[n] 的值。
class Solution {
public:int waysToStep(int n) {//判斷邊界情況if(n==0|n==1) return 1;if(n==2) return 2;vector<int> dp(n+1);//初始化dp[0]=1,dp[1]=1,dp[2]=2;for(int i=3;i<=n;i++){//取模操作防止數據溢出dp[i]=((dp[i-1]+dp[i-2])%1000000007+dp[i-3])%1000000007;}return dp[n];}
};
三. (746.) 使?最?花費爬樓梯(力扣)

注意:數組內的每?個下標 [0, n - 1] 表?的都是樓層,?頂樓的位置其實是在 n 的位置!
3.1算法原理
解法1
1.狀態表示
dp[i] 表?:到達 i 位置時的最?花費。(注意:到達 i 位置的時候, i 位置的錢不需要算上)
2.狀態轉移方程
根據最近的?步,分情況討論:
? 先到達 i - 1 的位置,然后?付 cost[i - 1] ,接下來??步?到 i 位置:dp[i - 1] + csot[i - 1]
? 先到達 i - 2 的位置,然后?付 cost[i - 2] ,接下來??步?到 i 位置:dp[i - 2] + csot[i - 2]
- 初始化:
從遞推公式可以看出,需要先初始化 i = 0 ,以及 i = 1 位置的值。容易得到dp[0] = dp[1] = 0 ,因為不需要任何花費,就可以直接站在第 0 層和第 1 層上
- 填表順序:
根據「狀態轉移?程」可得,遍歷的順序是「從左往右」
- 返回值:
根據「狀態表?以及題?要求」,需要返回 dp[n] 位置的值。
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n+1);//初始化dp[0]=dp[1]=0;for(int i=2;i<=n;i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[n];}
};
解法2
- 狀態表?:
dp[i] 表?:從 i 位置出發,到達樓頂,此時的最?花費。
- 狀態轉移?程:
根據最近的?步,分情況討論:
? ?付 cost[i] ,往后??步,接下來從 i + 1 的位置出發到終點: dp[i + 1] + cost[i]
? ?付 cost[i] ,往后?兩步,接下來從 i + 2 的位置出發到終點: dp[i + 2] + cost[i]
我們要的是最?花費,因此 dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i] 。
- 初始化:
為了保證填表的時候不越界,我們需要初始化最后兩個位置的值,結合狀態表?易得: dp[n - 1] = cost[n - 1], dp[n - 2] = cost[n - 2]
- 填表順序:
根據「狀態轉移?程」可得,遍歷的順序是「從右往左」。
- 返回值:
根據「狀態表?以及題?要求」,需要返回 dp[n] 位置的值。注意,此時不需要多開辟一個空間,因為根據狀態表示從n位置到n位置原地踏步的最小花費為0
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int> dp(n);//初始化dp[n-1]=cost[n-1];dp[n-2]=cost[n-2];for(int i=n-3;i>=0;i--)//從右往左初始化{dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i]);}return min(dp[0],dp[1]);}
};
注意狀態表示可以是多個的,如果能推得狀態轉移方程并且最后運行通過,證明該種狀態表示是正確的
四. (91.) 解碼?法(力扣)
4.1算法原理
- 狀態表?:
根據以往的經驗,對于?多數線性 dp ,經驗上都是「以某個位置結束或者開始」做?章,這?繼續嘗試「? i 位置為結尾」結合「題?要求」來定義狀態表?。dp[i] 表?:字符串中 [0,i] 區間上,?共有多少種編碼?法。
2.狀態轉移方程:
關于 i 位置的編碼狀況,我們可以分為下?兩種情況:
i. 讓 i 位置上的數單獨解碼成?個字?;
ii. 讓 i 位置上的數與 i - 1 位置上的數結合,解碼成?個字?
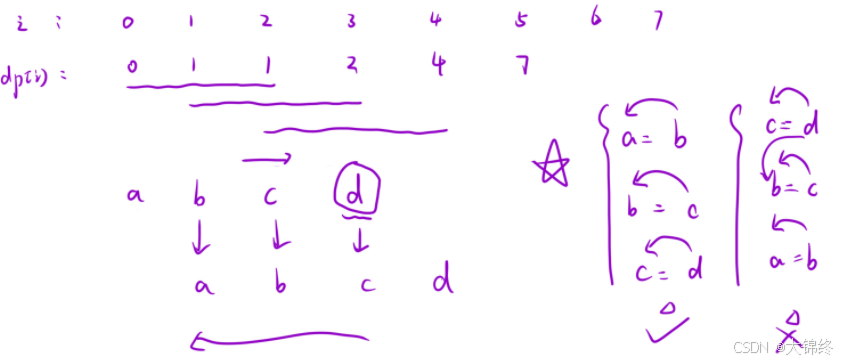
由狀態定義不用考慮i+1位置的編碼,i和i-1位置的解碼都有成功和失敗兩種可能。
解碼成功:
解碼方法等于前一位區間上的解碼方法,相當于前一位區間上所由解碼結果后面再加上當前位置解碼后的字母即可
解碼失敗:
說明當前位置上不能單獨解碼或結合解碼,之前的努力都白費了
3.初始化
由于可能要?到 i - 1 以及 i - 2 位置上的 dp 值,因此要先初始化「前兩個位置」。
初始化 dp[0] :結果有0,1
i. 當 s[0] == ‘0’ 時,沒有編碼?法,結果 dp[0] = 0 ;
ii. 當 s[0] != ‘0’ 時,能編碼成功, dp[0] = 1
初始化 dp[1] :結果有0,1,2
i. 當 s[1] 在 [1,9] 之間時,能單獨編碼,此時 dp[1] += dp[0] (原因同上,
dp[1] 默認為 0 )
ii. 當 s[0] 與 s[1] 結合后的數在 [10, 26] 之間時,說明在前兩個字符中,?有?種
編碼?式,此時 dp[1] += 1
- 填表順序:
「從左往右」
- 返回值:
應該返回 dp[n - 1] 的值,表?在 [0, n - 1] 區間上的編碼?法。
class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int> dp(n);//初始化if(s[0]!='0') dp[0]=1;//處理邊界情況if(n==1) return dp[0];if(s[0]!='0'&&s[1]!='0') dp[1]=1;//注意條件判斷時不能連續比較int t=(s[0]-'0')*10+(s[1]-'0');if(10<=t&&t<=26) dp[1]+=1;//填表for(int i=2;i<n;i++){//解碼當前位置,單獨if(s[i]!='0') dp[i]+=dp[i-1];//與上一位置共同解碼int t=(s[i-1]-'0')*10+(s[i]-'0');if(10<=t&&t<=26) dp[i]+=dp[i-2];}return dp[n-1];}
};
可以看出上述代碼初始化部分和循環部分代碼有些重復,特別是初始化dp[1]位置時有三種情況需要判斷,可以優化
4.2細節優化
dp表中多開辟一位,將dp[0]設置為輔助節點來初始化,這樣原dp表中dp[1]位置初始化的復雜條件判斷就可以避免,放到循環中去完成賦值,簡化了一次操作
注意:
1.輔助節點中的值要保證后面的填表是正確的
已知會先初始化兩個節點,一個為輔助節點(新dp表中dp[0]),另一個為舊dp表中的dp[0]新dp表中的dp[1]。填表前會先判斷解碼,單獨解碼時與前一個節點有關與輔助節點無關,但與前一節點共同解碼時成功后會加上前前節點的解碼方法數,所以此時與輔助節點有關,該情況下輔助節點應設為1而不是0
2.下標的映射關系
由于dp表中多增一位,在查找原表進行解碼時下標位置要-1才能相對應
class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int> dp(n+1);//初始化dp[0]=1;// 保證后續填表是正確的dp[1] = s[0] != '0';//填表for(int i=2;i<=n;i++){//解碼當前位置,單獨if(s[i-1]!='0') dp[i]+=dp[i-1];//與上一位置共同解碼int t=(s[i-2]-'0')*10+(s[i-1]-'0');//改變下標映射關系if(10<=t&&t<=26) dp[i]+=dp[i-2];}return dp[n];}
};

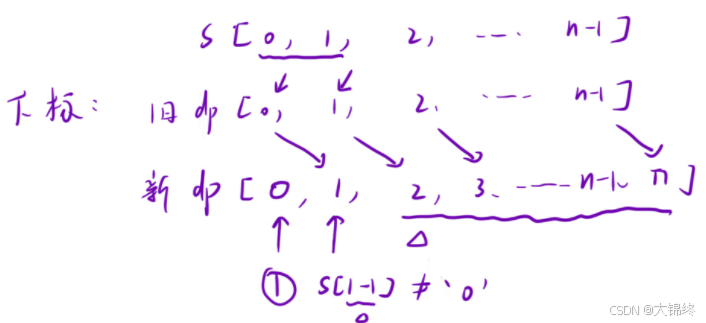



)



后端)



)
)





)
