📘 進制定義與轉換詳解

一、進制的含義

進制，也稱為進位計數制，是一種人為定義的、帶進位的計數方法。每種進制都有其基數（Base），表示該進制下使用的不同數字個數。

• X進制：每一位上的數字運算時都是逢X進一。
  • 十進制：逢十進一
  • 二進制：逢二進一
  • 八進制：逢八進一
  • 十六進制：逢十六進一
  • ……

💡 小知識：也有不帶進位的計數法，如“正”字計數、結繩記事等，但進制是現代數學和計算機中廣泛使用的標準計數方式。

---

二、常見進制介紹

1. 十進制（Decimal，Base-10）

• 基數：10
• 符號：0 ~ 9
• 權重：10的冪次方
• 示例：
  $$1234=1\times 10^3+2\times 10^2+3\times 10^1+4\times 10^0$$

2. 二進制（Binary，Base-2）

• 基數：2
• 符號：0、1
• 權重：2的冪次方
• 用途：計算機底層表示數據的基本單位（0表示關，1表示開）
• 示例：
  $$100_2=1\times 2^2+0\times 2^1+0\times 2^0=4_{10}$$
• 表示方式：前綴 0B

  int val = 0B100;  // 表示十進制4
  

3. 八進制（Octal，Base-8）

• 基數：8
• 符號：0 ~ 7
• 權重：8的冪次方
• 用途：早期計算機系統中常用，每個八進制位對應3個二進制位
• 示例：
  $$123_8=1\times 8^2+2\times 8^1+3\times 8^0=83_{10}$$
• 表示方式：前綴 0

  int val = 0123;  // 表示十進制83
  

4. 十六進制（Hexadecimal，Base-16）

• 基數：16
• 符號：0 ~ 9 和 A ~ F（或 a ~ f），其中：
  • A = 10，B = 11，C = 12，D = 13，E = 14，F = 15
• 權重：16的冪次方
• 用途：常用于內存地址、顏色編碼等，每個十六進制位對應4個二進制位
• 示例：
  $$1a2b3c_{16}=1\times 16^5+10\times 16^4+2\times 16^3+11\times 16^2+3\times 16^1+12\times 16^0=1715004_{10}$$
• 表示方式：前綴 0x

  int val = 0x1a2b3c;  // 表示十進制1715004
  

---

三、進制之間的轉換

1. 任意進制 → 十進制

通用公式：

設某進制數為 xyzw...N，其十進制值為：

$$\text{Value}=x\times B^{n?1}+y\times B^{n?2}+z\times B^{n?3}+?+N\times B^0$$

其中：

• $ B $：進制基數
• $ n $：數字位數

示例：

• 二進制 0B100：
  $$1\times 2^2+0\times 2^1+0\times 2^0=4$$

• 八進制 0123：
  $$1\times 8^2+2\times 8^1+3\times 8^0=83$$

• 十六進制 0x1a2b3c：
  $$1\times 16^5+10\times 16^4+2\times 16^3+11\times 16^2+3\times 16^1+12\times 16^0=1715004$$

---

2. 十進制 → 任意進制

方法：除基取余法（從下往上讀）

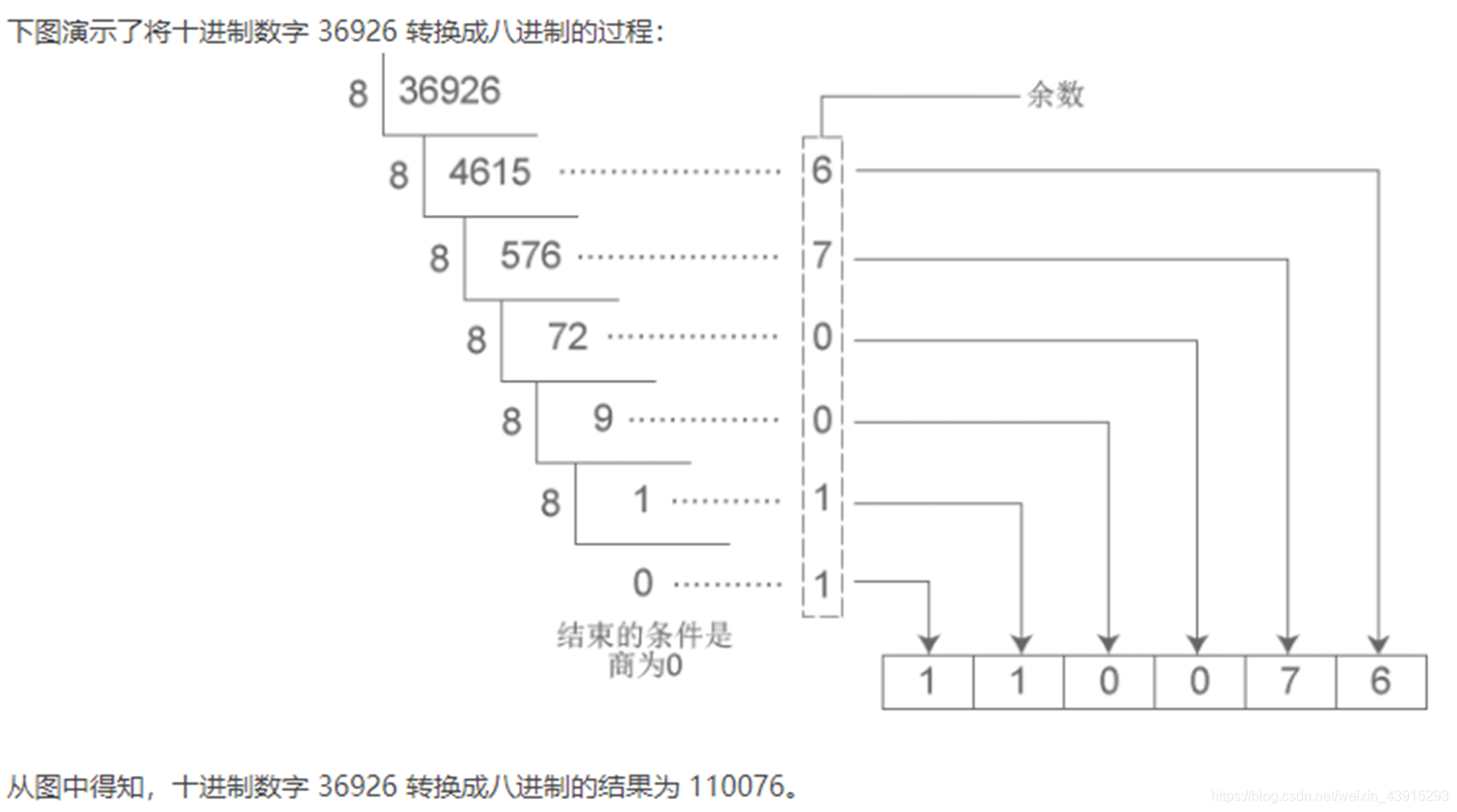
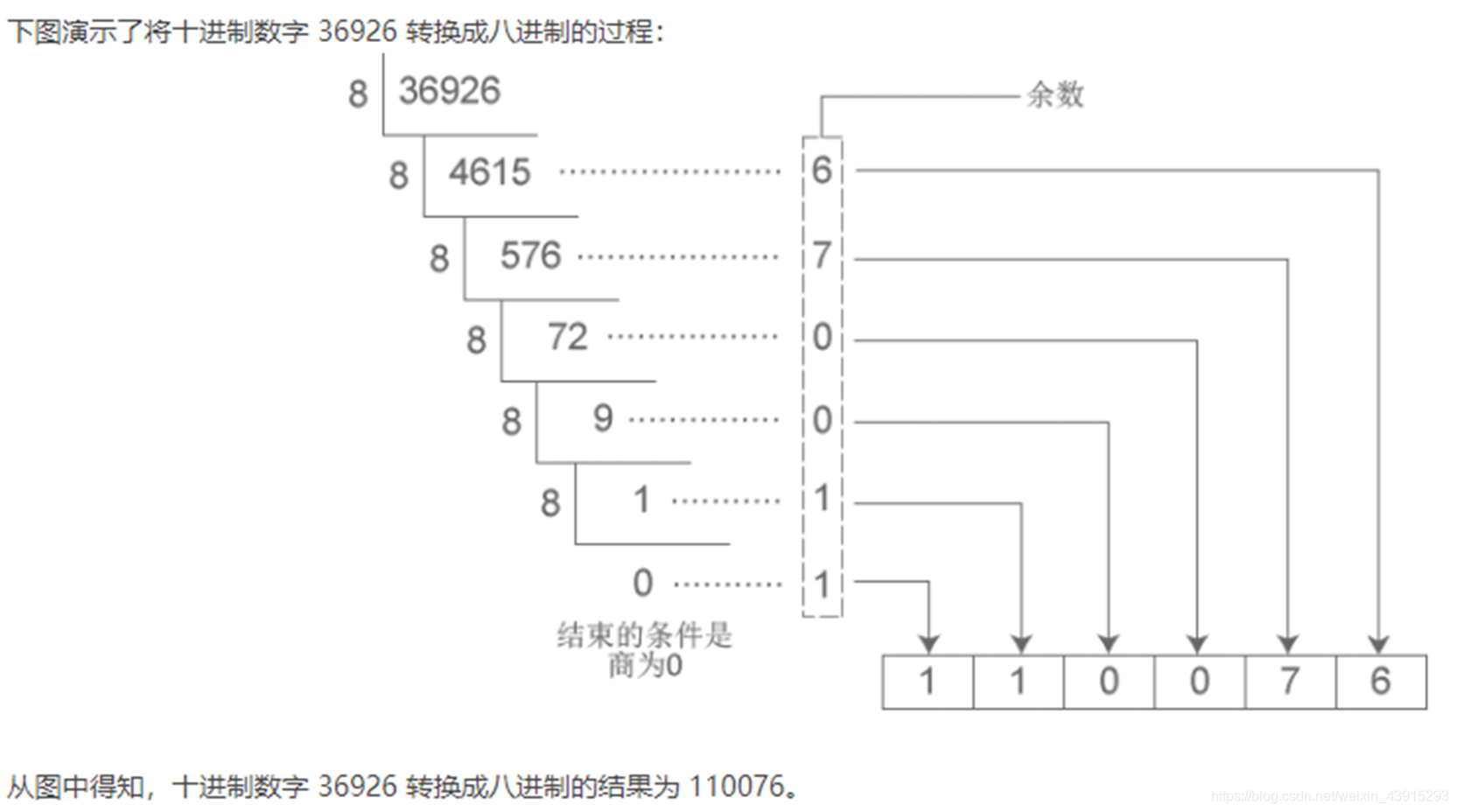
示例：十進制 123 → 二進制

123 ÷ 2 = 61 余 1
61  ÷ 2 = 30 余 1
30  ÷ 2 = 15 余 0
15  ÷ 2 = 7  余 1
7   ÷ 2 = 3  余 1
3   ÷ 2 = 1  余 1
1   ÷ 2 = 0  余 1

從下往上讀取余數：1111011，補全為8位：0B01111011

示例：十進制 100 → 八進制

100 ÷ 8 = 12 余 4
12  ÷ 8 = 1  余 4
1   ÷ 8 = 0  余 1

結果：0144

示例：十進制 123 → 十六進制

123 ÷ 16 = 7 余 11（B）
7   ÷ 16 = 0 余 7

結果：0x7b

---

3. 二進制與其他進制的快速轉換

a. 二進制 → 八進制

• 原理：3位二進制 = 1位八進制（因為 $2^3=8$）
• 方法：從右往左每3位一組，不足補0，每組轉為八進制數

示例：

二進制：0B10100101011110011
分組：101 001 010 111 100 11（補0 → 011）
轉換：5   1   2   7   4   3
結果：0512743

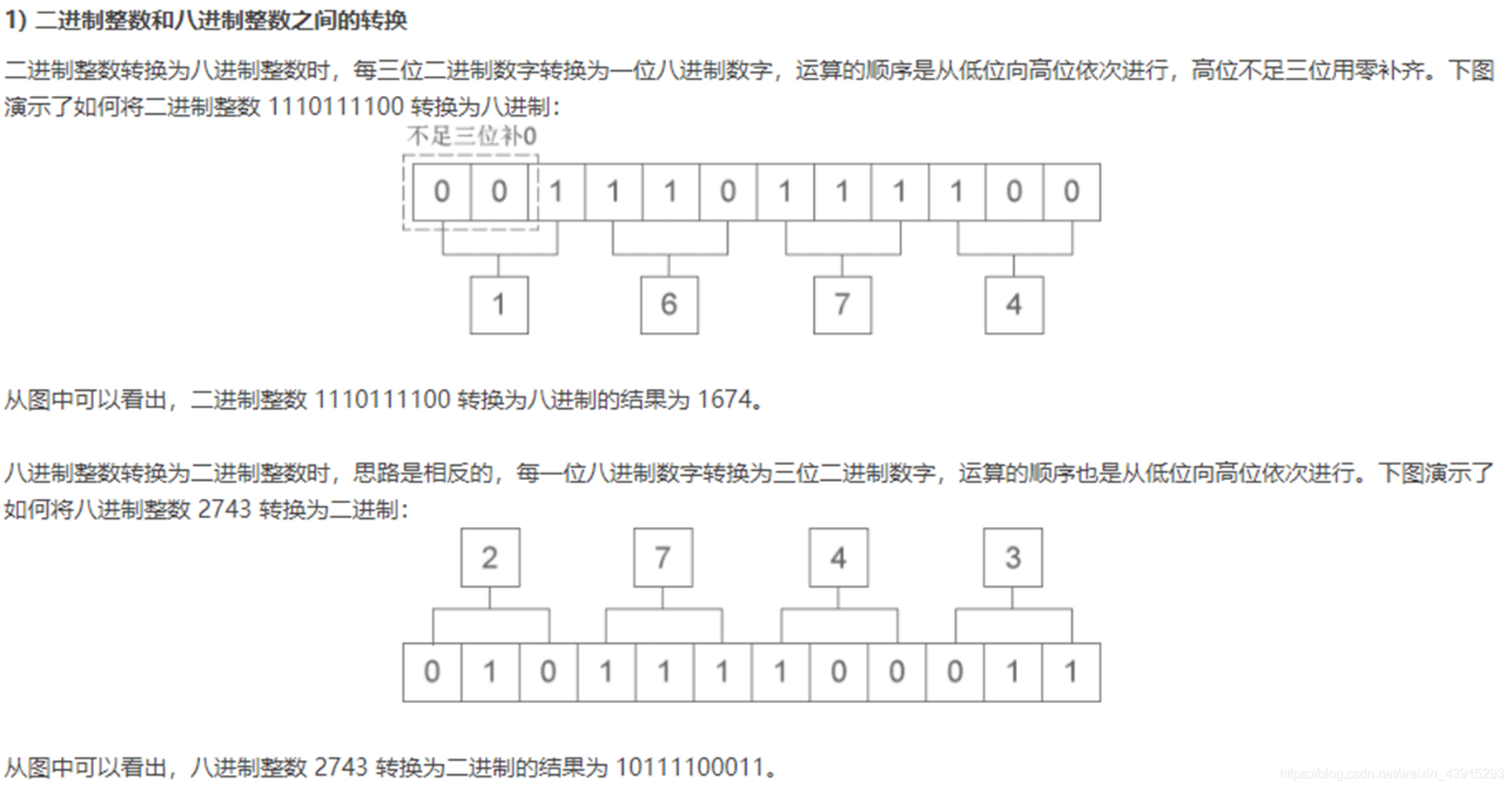
b. 二進制 → 十六進制

• 原理：4位二進制 = 1位十六進制（因為 $2^4=16$）
• 方法：從右往左每4位一組，不足補0，每組轉為十六進制數

示例：

二進制：0B00010101001010101010
分組：0001 0101 0010 1010 1010
轉換：1    5    2    A    A
結果：0x152AA

---

四、負數的表示（以二進制為例）

在計算機中，負數使用補碼表示。

步驟：

1. 求原碼：正數的二進制表示
2. 求反碼：按位取反（符號位不變）
3. 求補碼：反碼 + 1

示例：-100 的二進制表示

1. 原碼：100 = 01100100（假設8位）
2. 反碼：10011011
3. 補碼：10011100

所以，-100 的二進制補碼表示為：0B10011100

---

五、總結

進制	基數	符號范圍	表示前綴	特點
十進制	10	0~9	無	日常使用
二進制	2	0,1	0B	計算機基礎
八進制	8	0~7	0	簡化二進制
十六進制	16	0~9, A~F	0x	內存地址、顏色代碼

---

進制加減法

以下是對進制加減法相關內容的優化敘述，邏輯更清晰、結構更嚴謹：

---

進制基礎與加減法運算規則

在計算機科學和編程中，理解不同進制及其運算規則是非常重要的基礎知識。常見的進制包括二進制、八進制、十進制和十六進制。它們的核心區別在于所使用的數字范圍和進位規則。

---

一、二進制（Binary）

• 表示方式：使用兩個數字 0 和 1 來表示數值。
• 應用場景：計算機內部所有數據都以二進制形式存儲和處理。
• 加法規則：逢二進一。
  例如：1 + 1 = 10
• 減法規則：借一當二。
  例如：10 - 1 = 1

---

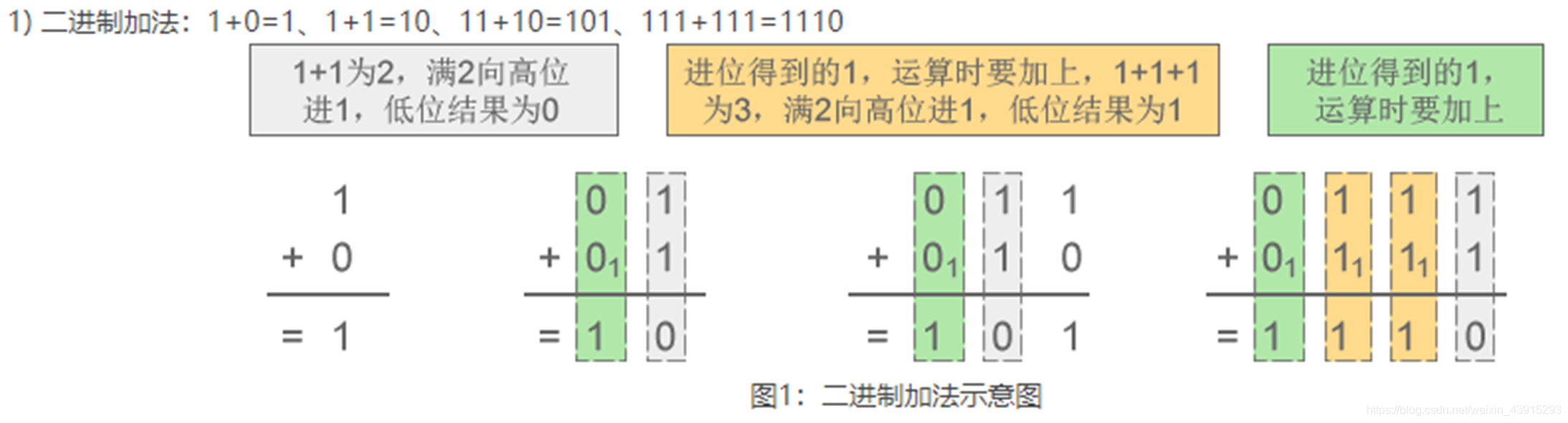
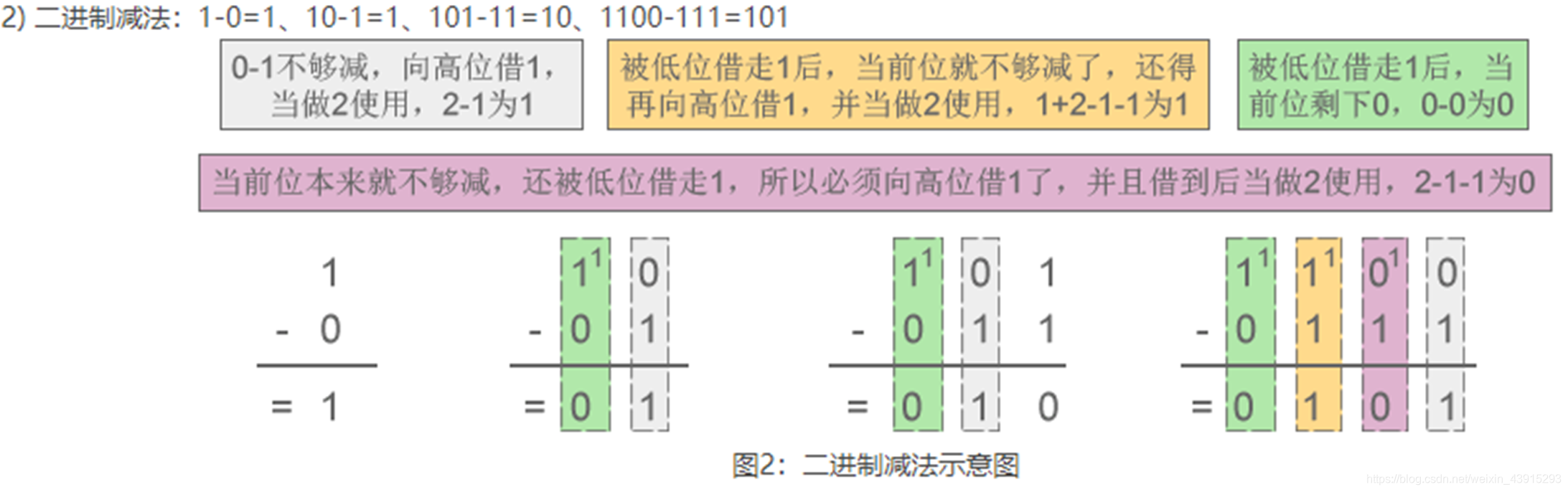
二、八進制（Octal）

• 表示方式：使用八個數字 0 到 7 來表示數值。
• 加法規則：逢八進一。
  例如：7 + 1 = 10
• 減法規則：借一當八。
  例如：10 - 1 = 7

---

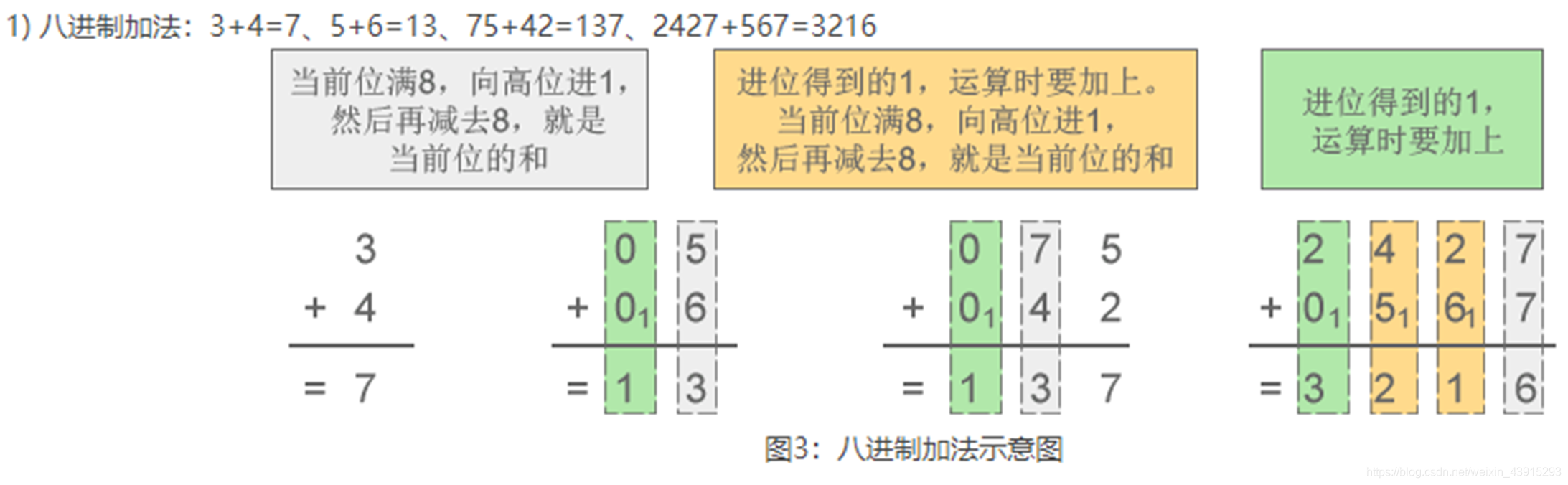
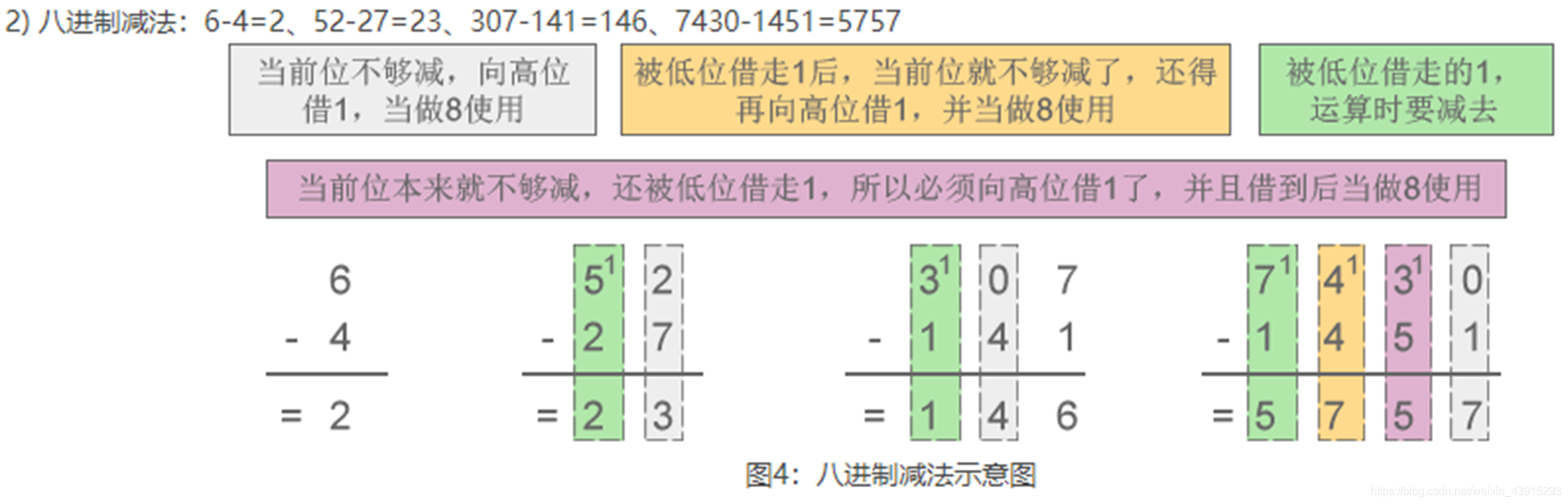
三、十進制（Decimal）

• 表示方式：使用十個數字 0 到 9 來表示數值。
• 加法規則：逢十進一。
• 減法規則：借一當十。

---

四、十六進制（Hexadecimal）

• 表示方式：使用數字 0 到 9 和字母 A 到 F 來表示數值。
  其中：
  • A = 10
  • B = 11
  • C = 12
  • D = 13
  • E = 14
  • F = 15
• 字母說明：不區分大小寫，ABCDEF 也可以寫作 abcdef。
• 加法規則：逢十六進一。
  例如：F + 1 = 10
• 減法規則：借一當十六。
  例如：10 - 1 = F

---

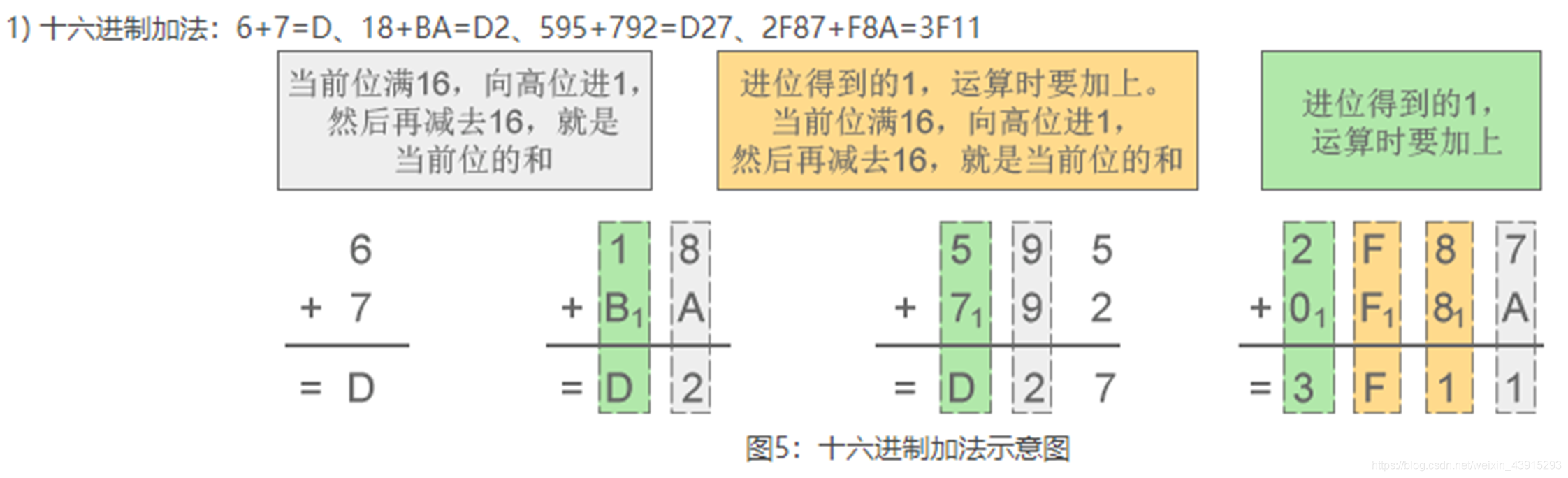
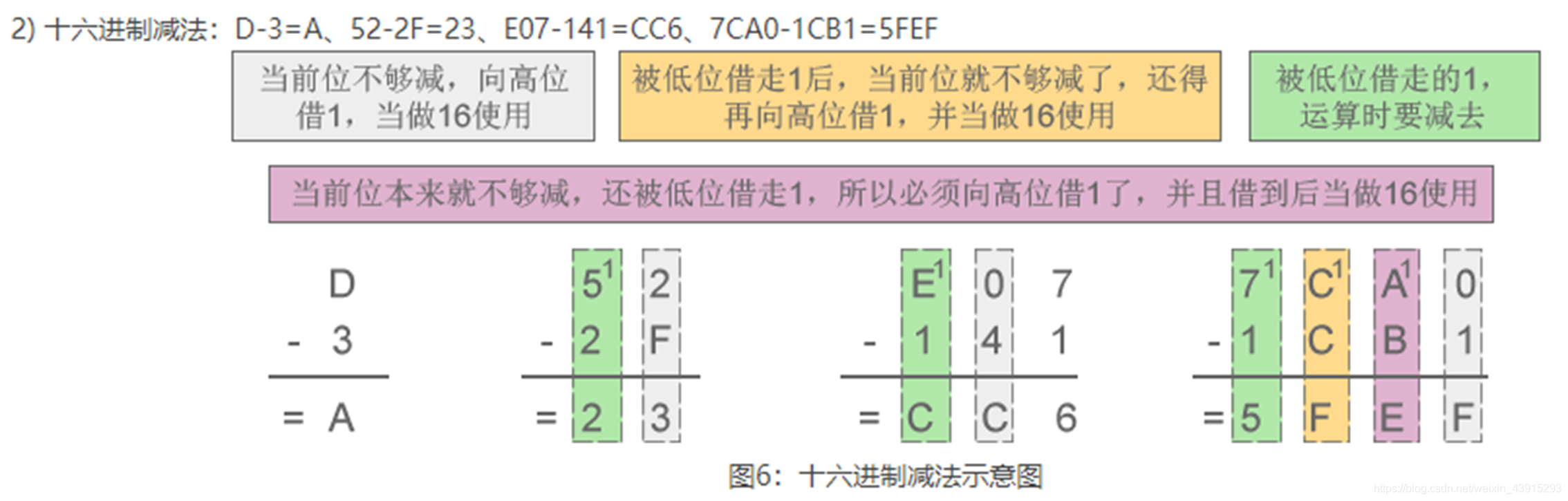
總結

不同進制的加減法遵循相同的邏輯：

• 加法：當前位滿“基數”就向前一位進一；
• 減法：當前位不夠減時，向高位借一，相當于借了“基數”。

掌握這些規則，有助于理解數據在計算機中的表示和處理方式，是學習編程和計算機系統的重要基礎。

進制對照表