30天打好數模基礎-邏輯回歸講解

案例代碼實現

一、代碼說明

本案例針對信用卡欺詐檢測二分類問題，完整實現邏輯回歸的數據生成→預處理→模型訓練→評估→閾值調整→決策邊界可視化流程。

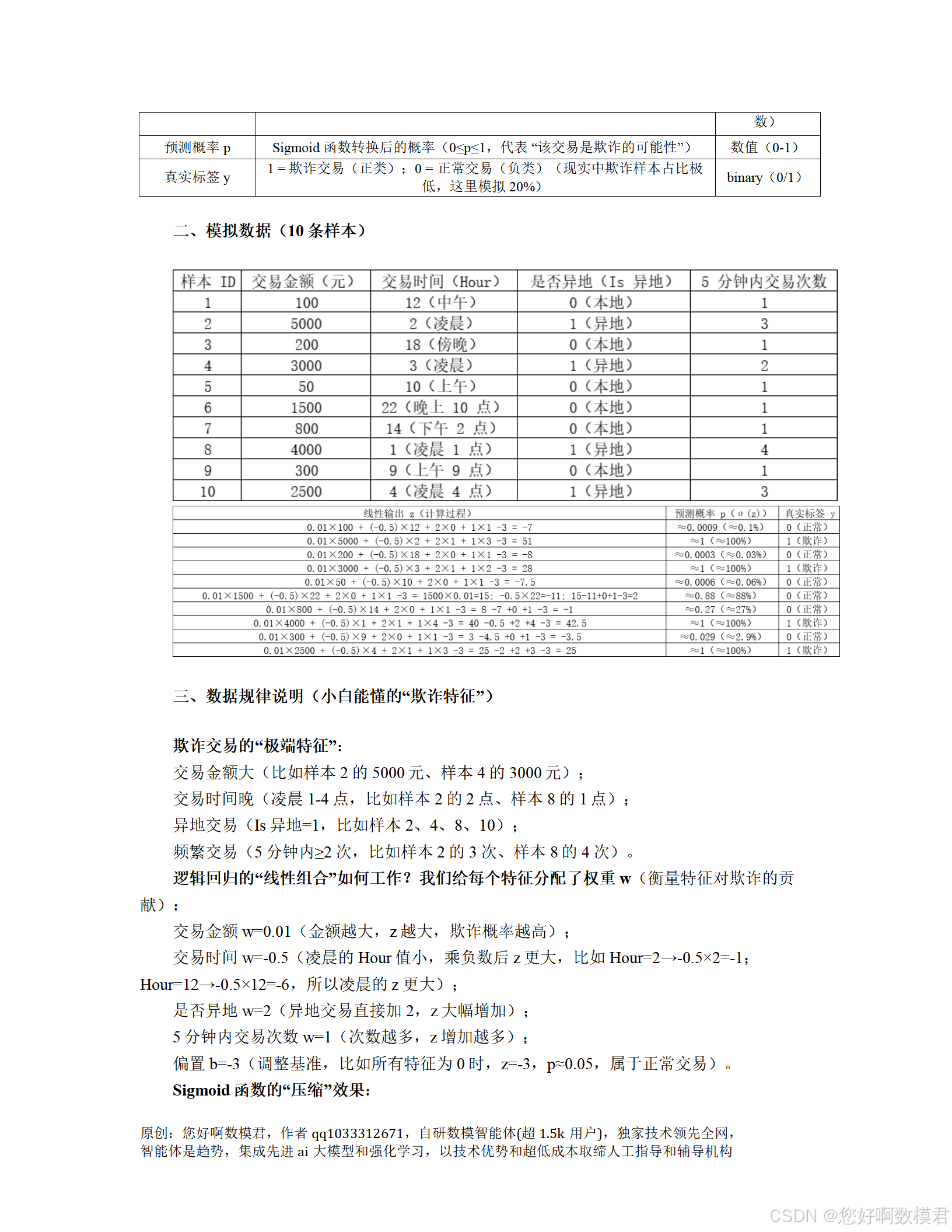
數據生成：模擬1000條交易數據，其中欺詐樣本占20%（類不平衡），特征包括交易金額、時間、是否異地、5分鐘內交易次數。

預處理：標準化特征（避免尺度差異影響模型）。

模型訓練：使用邏輯回歸，通過class_weight處理類不平衡。

評估：計算精確率、召回率、F1-score，繪制ROC/PR曲線。

閾值調整：對比默認閾值（0.5）與高精確率閾值（0.7）的性能。

決策邊界可視化：選取2個關鍵特征（交易金額、時間），繪制邏輯回歸的決策邊界（p=0.5）。

二、完整代碼

# 導入必要庫（小白需記住這些常用庫）
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import (classification_report, roc_curve, auc,precision_recall_curve, confusion_matrix)# 設置隨機種子（保證結果可重復）
np.random.seed(42)def generate_credit_card_data(n_samples=1000, fraud_ratio=0.2):"""生成信用卡交易模擬數據（小白重點理解特征分布差異）參數：n_samples: 總樣本量fraud_ratio: 欺詐樣本比例（類不平衡）返回：df: 包含特征和標簽的DataFrame"""# 計算正常/欺詐樣本量n_fraud = int(n_samples * fraud_ratio)n_normal = n_samples - n_fraud# ---------------------- 1. 生成正常交易數據（0類） ----------------------normal_data = {'金額': np.random.normal(loc=1000, scale=200, size=n_normal),  # 正常金額：均值1000，標準差200'時間': np.random.randint(low=10, high=21, size=n_normal),       # 正常時間：10-20點（白天）'是否異地': np.random.binomial(n=1, p=0.1, size=n_normal),        # 正常異地：10%概率'5分鐘內交易次數': np.random.poisson(lam=1, size=n_normal)         # 正常次數：均值1次}normal_df = pd.DataFrame(normal_data)normal_df['標簽'] = 0  # 0=正常# ---------------------- 2. 生成欺詐交易數據（1類） ----------------------fraud_data = {'金額': np.random.normal(loc=5000, scale=1000, size=n_fraud), # 欺詐金額：均值5000，標準差1000（更大）'時間': np.random.randint(low=0, high=6, size=n_fraud),        # 欺詐時間：0-5點（凌晨）'是否異地': np.random.binomial(n=1, p=0.8, size=n_fraud),        # 欺詐異地：80%概率（更高）'5分鐘內交易次數': np.random.poisson(lam=3, size=n_fraud)         # 欺詐次數：均值3次（更頻繁）}fraud_df = pd.DataFrame(fraud_data)fraud_df['標簽'] = 1  # 1=欺詐# ---------------------- 3. 合并數據并打亂順序 ----------------------df = pd.concat([normal_df, fraud_df], ignore_index=True)df = df.sample(frac=1, random_state=42).reset_index(drop=True)  # 打亂順序return dfdef plot_roc_pr_curve(y_true, y_prob):"""繪制ROC曲線和PR曲線（評估模型性能的關鍵圖）"""# ROC曲線fpr, tpr, _ = roc_curve(y_true, y_prob)roc_auc = auc(fpr, tpr)# PR曲線precision, recall, _ = precision_recall_curve(y_true, y_prob)# 繪圖fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))# ROC曲線ax1.plot(fpr, tpr, color='blue', label=f'ROC曲線 (AUC={roc_auc:.2f})')ax1.plot([0, 1], [0, 1], color='gray', linestyle='--', label='隨機猜測')ax1.set_xlabel('假陽性率（FPR）')ax1.set_ylabel('真陽性率（TPR）')ax1.set_title('ROC曲線（評估整體區分能力）')ax1.legend()# PR曲線ax2.plot(recall, precision, color='green', label='PR曲線')ax2.set_xlabel('召回率（Recall）')ax2.set_ylabel('精確率（Precision）')ax2.set_title('PR曲線（評估類不平衡下的性能）')ax2.legend()plt.tight_layout()plt.show()def plot_decision_boundary(model, X, y, scaler, feature1='金額', feature2='時間'):"""繪制邏輯回歸的決策邊界（小白重點理解：線性模型如何劃分類別）參數：model: 訓練好的邏輯回歸模型X: 特征數據（DataFrame）y: 標簽數據scaler: 訓練集的標準化器（用于網格數據標準化）feature1: 橫軸特征feature2: 縱軸特征"""# 選取兩個特征，固定其他特征為均值（或模式）# 其他特征：是否異地（取0，本地）、5分鐘內交易次數（取1，正常次數）fixed_features = {'是否異地': 0,'5分鐘內交易次數': 1}# 生成網格點（覆蓋兩個特征的取值范圍）x1 = np.linspace(X[feature1].min(), X[feature1].max(), 100)x2 = np.linspace(X[feature2].min(), X[feature2].max(), 100)X1, X2 = np.meshgrid(x1, x2)# 構造網格點的特征數據（包含固定特征，保持與原數據列順序一致）grid_data = pd.DataFrame({feature1: X1.ravel(),feature2: X2.ravel(),**fixed_features})# 調整列順序與原數據一致（避免標準化時特征順序錯誤）grid_data = grid_data[X.columns]# 標準化網格點特征（使用訓練集的標準化器）grid_data_scaled = scaler.transform(grid_data)# 預測網格點的概率（p=0.5是決策邊界）y_prob_grid = model.predict_proba(grid_data_scaled)[:, 1]y_prob_grid = y_prob_grid.reshape(X1.shape)# 繪制決策邊界（p=0.5的等高線）plt.figure(figsize=(10, 6))contour = plt.contourf(X1, X2, y_prob_grid, levels=[0, 0.5, 1], cmap='RdBu', alpha=0.3)plt.colorbar(contour, label='欺詐概率')# 繪制樣本點（正常=藍色，欺詐=紅色）sns.scatterplot(x=X[feature1], y=X[feature2], hue=y, palette={0: 'blue', 1: 'red'}, alpha=0.7, edgecolor='black')# 添加標簽和標題plt.xlabel(feature1)plt.ylabel(feature2)plt.title(f'邏輯回歸決策邊界（{feature1} vs {feature2}）')plt.legend(title='標簽', labels=['正常', '欺詐'])plt.show()# ---------------------- 主程序：邏輯回歸完整流程 ----------------------
if __name__ == '__main__':# 1. 生成模擬數據（小白可調整n_samples和fraud_ratio）df = generate_credit_card_data(n_samples=1000, fraud_ratio=0.2)print("數據形狀：", df.shape)print("標簽分布：\n", df['標簽'].value_counts(normalize=True))  # 查看類不平衡情況（正常80%，欺詐20%）# 2. 劃分特征（X）和標簽（y）X = df.drop('標簽', axis=1)y = df['標簽']# 3. 拆分訓練集和測試集（70%訓練，30%測試）X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)print("訓練集形狀：", X_train.shape)print("測試集形狀：", X_test.shape)# 4. 特征標準化（避免尺度差異影響模型，必須fit在訓練集上）scaler = StandardScaler()X_train_scaled = scaler.fit_transform(X_train)X_test_scaled = scaler.transform(X_test)# 5. 訓練邏輯回歸模型（處理類不平衡：class_weight='balanced'）model = LogisticRegression(class_weight='balanced', random_state=42)model.fit(X_train_scaled, y_train)# 輸出模型參數（小白可解釋特征重要性）print("\n模型權重（w）：", model.coef_[0])print("模型偏置（b）：", model.intercept_[0])print("特征重要性（絕對值越大，對欺詐的貢獻越大）：")for feature, weight in zip(X.columns, model.coef_[0]):print(f"  {feature}: {weight:.2f}")# 6. 預測測試集（概率和類別）y_prob = model.predict_proba(X_test_scaled)[:, 1]  # 欺詐概率y_pred = model.predict(X_test_scaled)  # 默認閾值0.5的預測類別# 7. 評估模型性能（默認閾值0.5）print("\n---------------------- 默認閾值（0.5）評估 ----------------------")print("混淆矩陣：\n", confusion_matrix(y_test, y_pred))print(classification_report(y_test, y_pred))# 繪制ROC/PR曲線（評估整體性能）plot_roc_pr_curve(y_test, y_prob)# 8. 調整閾值（比如提高到0.7，追求高精確率，避免誤判正常交易）threshold = 0.7y_pred_high_precision = (y_prob >= threshold).astype(int)print(f"\n---------------------- 閾值={threshold}評估 ----------------------")print("混淆矩陣：\n", confusion_matrix(y_test, y_pred_high_precision))print(classification_report(y_test, y_pred_high_precision))# 9. 繪制決策邊界（選取“金額”和“時間”兩個關鍵特征，傳入標準化器）plot_decision_boundary(model, X_test, y_test, scaler, feature1='金額', feature2='時間')