上期回顧:【數據結構】樹(堆)·上
一.堆的應用
1.1堆排序(向下調整在上一期)
向上調整算法建堆:
首先先回顧一下向上調整算法
void AdjustUP(HPDataType* arr, int child)
{int parent = (child - 1) / 2;//找到父結點的位置while (child > 0)//循環,確保父結點一定小于(大于)子結點{//小堆:<//大堆:>// |// Vif (arr[child] > arr[parent]){//調整位置Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}在上一期我們也學過了向下調整算法建堆,其是通過由下向上循環,通過確保父結點下方的是堆結構,而向上算法建隊=堆就剛好反過來,是由上到下進行循環。
//堆排序
void HeapSort(int *arr,int n)
{//建堆--向下調整for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDOWN(arr, i, n);}//建堆--向上調整for (int i = 0; i < n; i++){AdjustUP(arr, i);}//排序int end = n - 1;while (end > 0){Swap(&arr[end], &arr[0]);AdjustDOWN(arr, 0, end);end--;}
}
1.2.TOP-K問題
TOP-K問題:即求數據結合中前K個最大的元素或者最小的元素,一般情況下數據量都比較大。
比如:專業前10名、世界500強、富豪榜、游戲中前100的活躍玩家等。
對于Top-K問題,能想到的最簡單直接的方式就是排序,但是:如果數據量非常大,排序就不太可取了(可能數據都不能一下子全部加載到內存中)。最佳的方式就是用堆來解決,基本思路如下:
通過前面的學習可了解到,小堆的堆頂是數據的最小值,所以若想通過小堆找最小,就需要遍歷所有的數據,在進行堆排序,這對于大數據肯定是不行的,
那么換一種思路,用小堆找最大數據:將前K個數據直接建小堆,然后再遍歷剩下的n-k個數據,將其與堆頂進行比較,若比堆頂大,則替換堆頂,來回重復,最后構成一個新堆,該堆就是數據中前K大的數。
而找前K小的數據道理相同,所以就可以總結出:
找最大的前K個數據,建小堆
找最小的前K個數據,建大堆
實踐:
先通過代碼生成10萬個數據,并保存在data.txt文件中
隨后實現topK函數:
void TopK()
{int k =0;printf("請輸入k:");scanf("%d", &k);const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen fail");exit(1);}//找最大的前K個數據--建小堆//找最小的前K個數據--建大堆int* minHeap = (int*)malloc(sizeof(int) * k);if (minHeap == NULL){perror("malloc fail");exit(1);}for (int i = 0; i < k; i++){fscanf(fout, "%d", &minHeap[i]);}//minHeap -- 向下調整建堆for (int i = (k - 2) / 2; i >=- 0; i--){//找最大的前K個數據--建小堆//找最小的前K個數據--建大堆AdjustDOWN(minHeap, i, k);}//遍歷剩下的n-k個數據,跟堆頂比較,堆頂小替換堆頂數據int x = 0;while (fscanf(fout, "%d", &x) != EOF){//找最大>//找最小<if (x > minHeap[0]){minHeap[0] = x;AdjustDOWN(minHeap, 0, k);}}for (int i = 0; i < k; i++){printf("%d ", minHeap[i]);}printf("\n");fclose(fout);
}先讀取文件數據,取前K個保存在數組中,并構成堆,隨后遍歷剩下的n-k個數據,進行比較替換。
最后成功打印
二.實現鏈式結構二叉樹
二叉樹的相關知識需要用到遞歸知識,所以建議先學習遞歸后再來看以下文章!!!

2.1二叉樹的插入與刪除
數據的插入和刪除可以在二叉樹的任何位置,所以此時暫時不寫文章,在后期學習到平衡樹,紅黑樹等在進行編寫。
2.2二叉樹的遍歷
二叉樹的遍歷有前序/中序/后序的遍歷的遞歸結構遍歷:
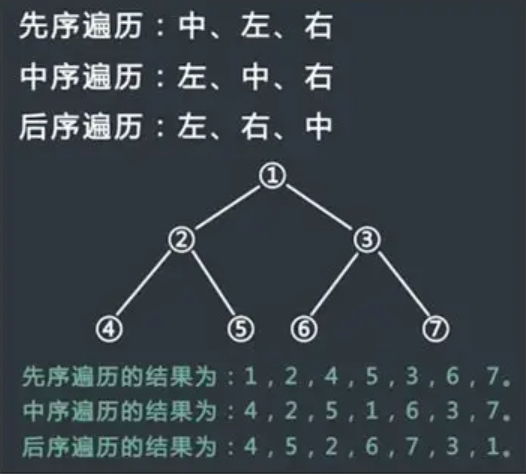
1)前序遍歷:訪問根節點的操作在遍歷其左右子樹之間
?訪問順序為:根結點、左子樹、右子樹
2)中序遍歷:訪問根結點的操作發生在遍歷其左右子樹之中(間)
訪問順序為:左子樹、根結點、右子樹
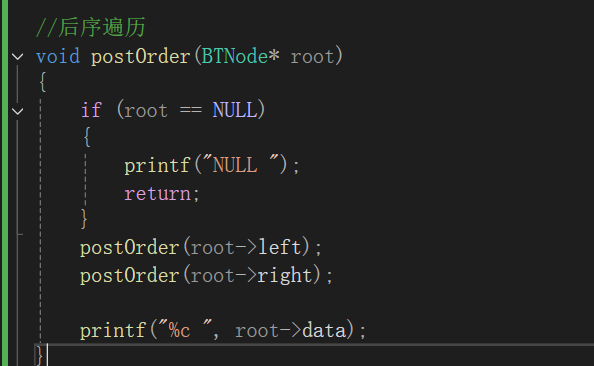
3)后序遍歷:訪問根結點的操作發生在遍歷其左右子樹之后
訪問順序為:左子樹、右子樹、根結點
遍歷的實現:
通過函數的遞歸實現遍歷,需要先判斷遞歸條件,當目前根節點為NULL時,遞歸中止,拿前序遍歷為例,在目前根節點時,先訪問根節點的data,隨后根據前序遍歷的順序,分別訪問左子樹,右子樹,進行遞歸。那么中序遍歷與后序遍歷也就很好寫出來了。


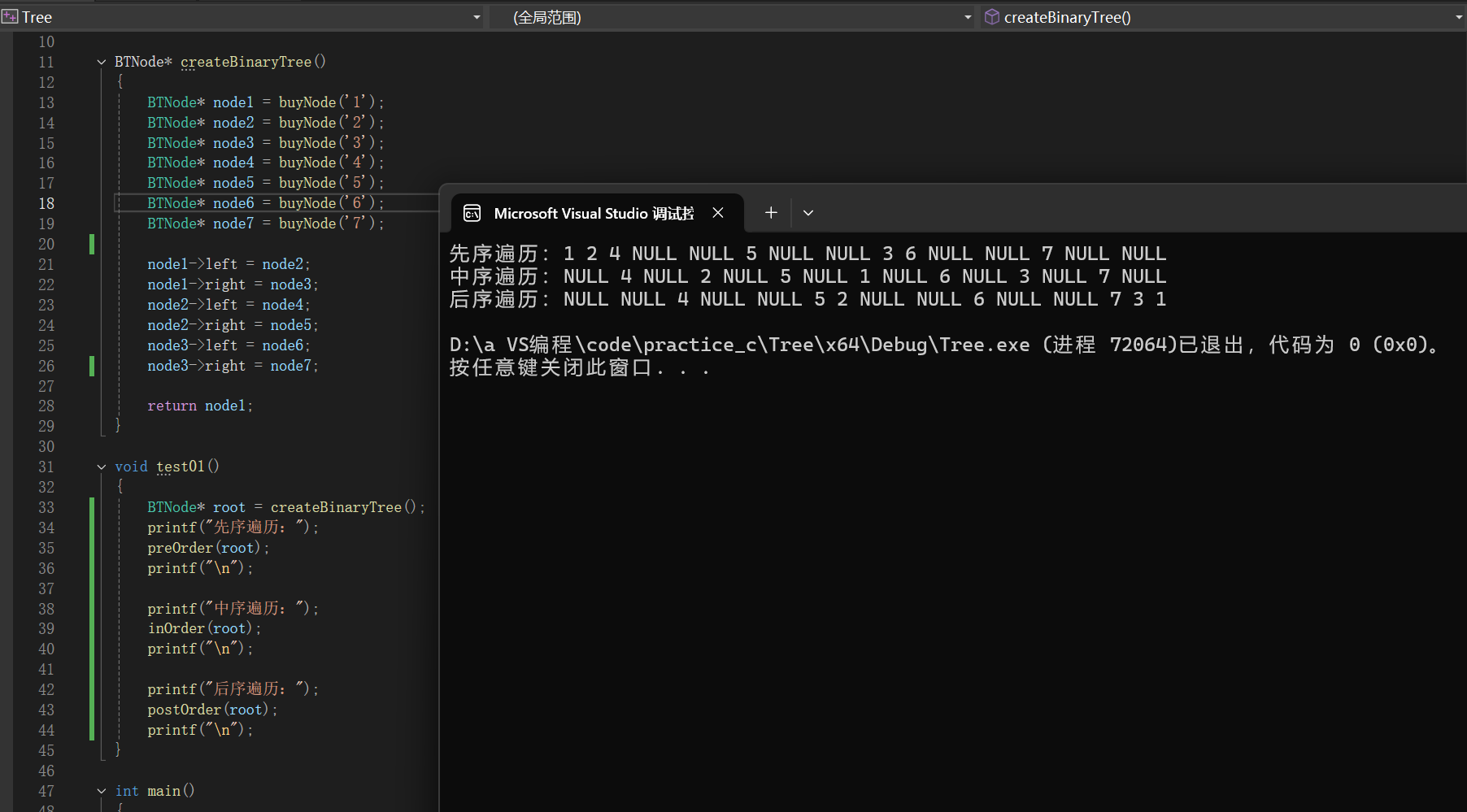
構造文章上文的二叉樹例子,然后進行遍歷輸出:
2.3二叉樹的結點個數
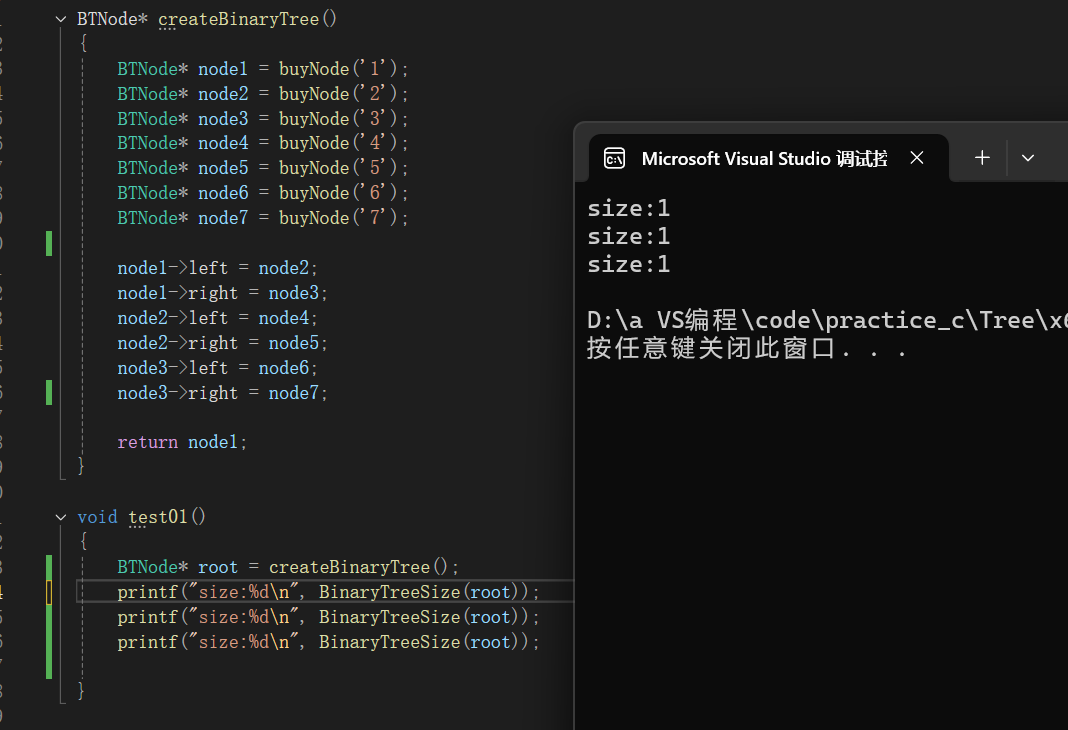
1.運用二叉樹遍歷的知識,通過遞歸遍歷每一個結點,然后size++,那么結果會是什么呢?
int BinaryTreeSize(BTNode* root)
{int size = 0;if (root == NULL){return;}//結點非空,+1size++;BinaryTreeSize(root->left);BinaryTreeSize(root->right);return size;
}運行后可以發現,不管調用幾次,size都為1,原因是因為,每次遞歸size都被初始化為0
2.那么把size設為全局變量后是不是就可以避免了?
int size = 0;
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return;}//結點非空,+1size++;BinaryTreeSize(root->left);BinaryTreeSize(root->right);return size;
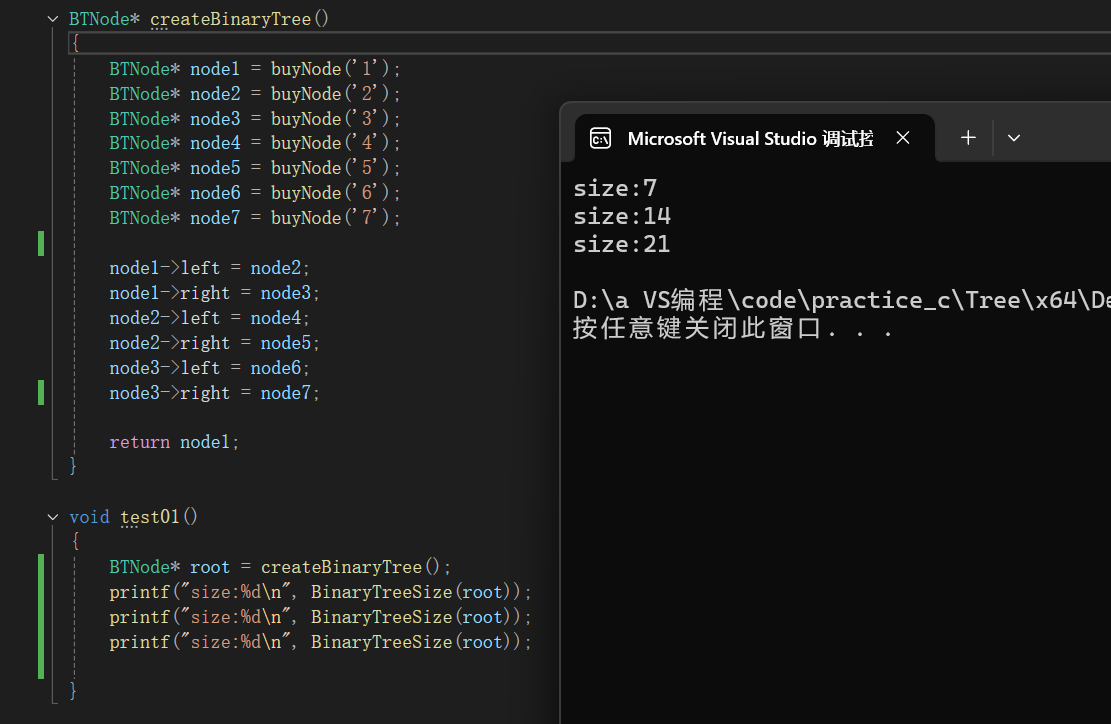
}運行后發現,雖然第一次調用size的結果是正確的,但是經過多次調用,size的值就會越加越大。
3.這次換一種思路,直接把size設為參數進行調用。
int BinaryTreeSize(BTNode* root, int size)
{if (root == NULL){return;}//結點非空,+1size++;BinaryTreeSize(root->left,size);BinaryTreeSize(root->right,size);return size;
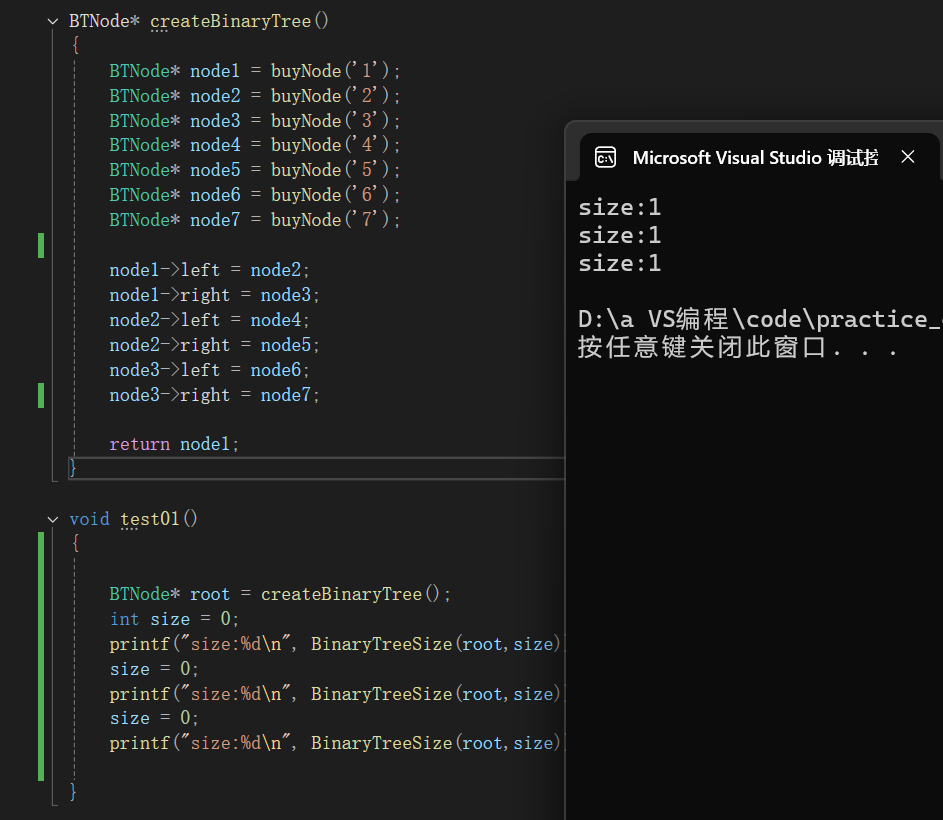
}這一次發現結果又變為三個1,分析原因,當遞歸回溯的時候,size的值會返回到上一步的值,例如當遞歸到4結點時,size=3,但是回溯到2結點時,size又回到了2
4.要解決這個問題,把傳值調用改為傳址調用就可解決。
int BinaryTreeSize(BTNode* root,int*size)
{if (root == NULL){return 0;}//結點非空,+1(*size)++ ;BinaryTreeSize(root->left,size);BinaryTreeSize(root->right,size);return *size;
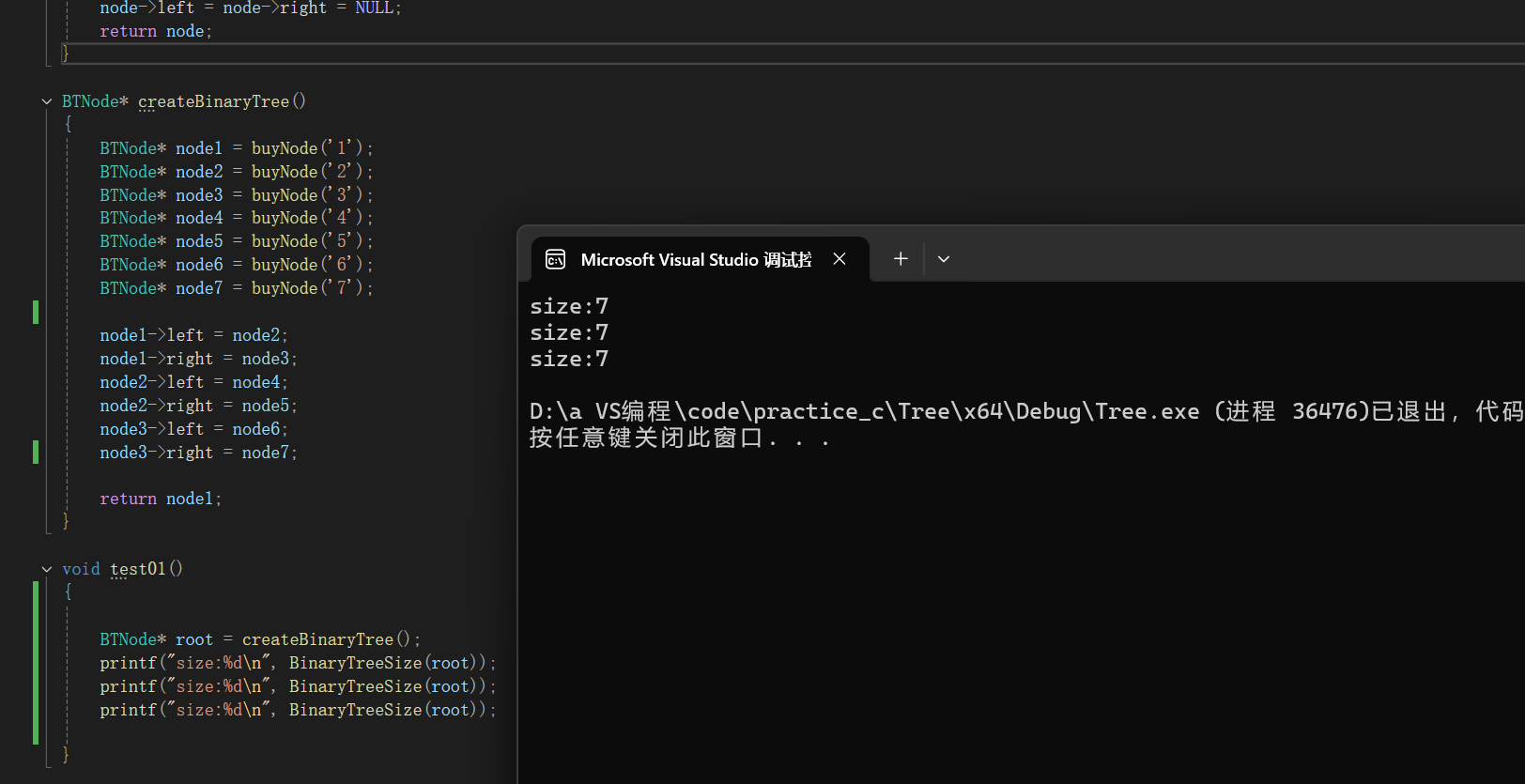
}這時結果就正確了,但是,每次調用參數,都需要把size初始化為0,有一點麻煩,在對函數進行改造
分析二叉樹可知,結點數 = 根結點+左子樹的結點數+右子樹的結點數?
最終版:
//二叉樹節點個數
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}//結點非空,+1return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}
2.4二叉樹葉子結點數
葉子結點數 = 左子樹葉子節點數 + 右子樹葉子結點數
結合剛才學到的結點數的知識,可以寫出:
//二叉樹葉子節點數
int BinaryTreeLeafSize(BTNode* root)
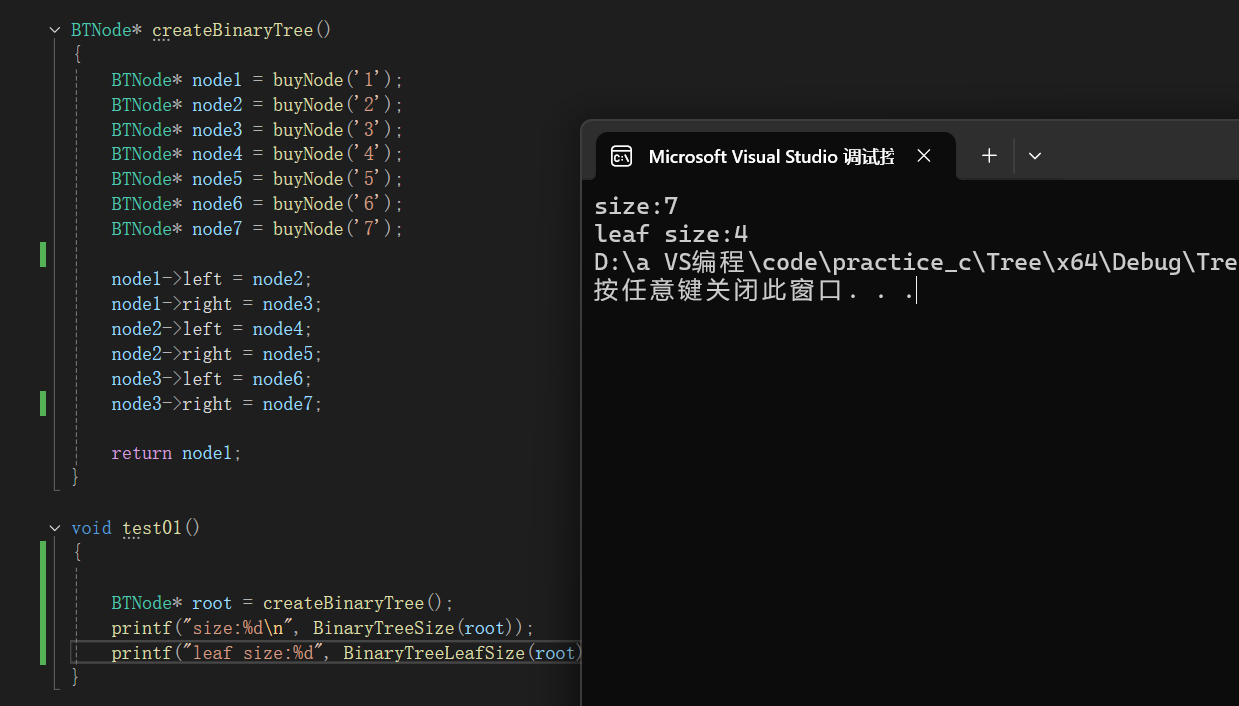
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
2.5二叉樹第K層結點個數
//二叉樹第K層結點個數
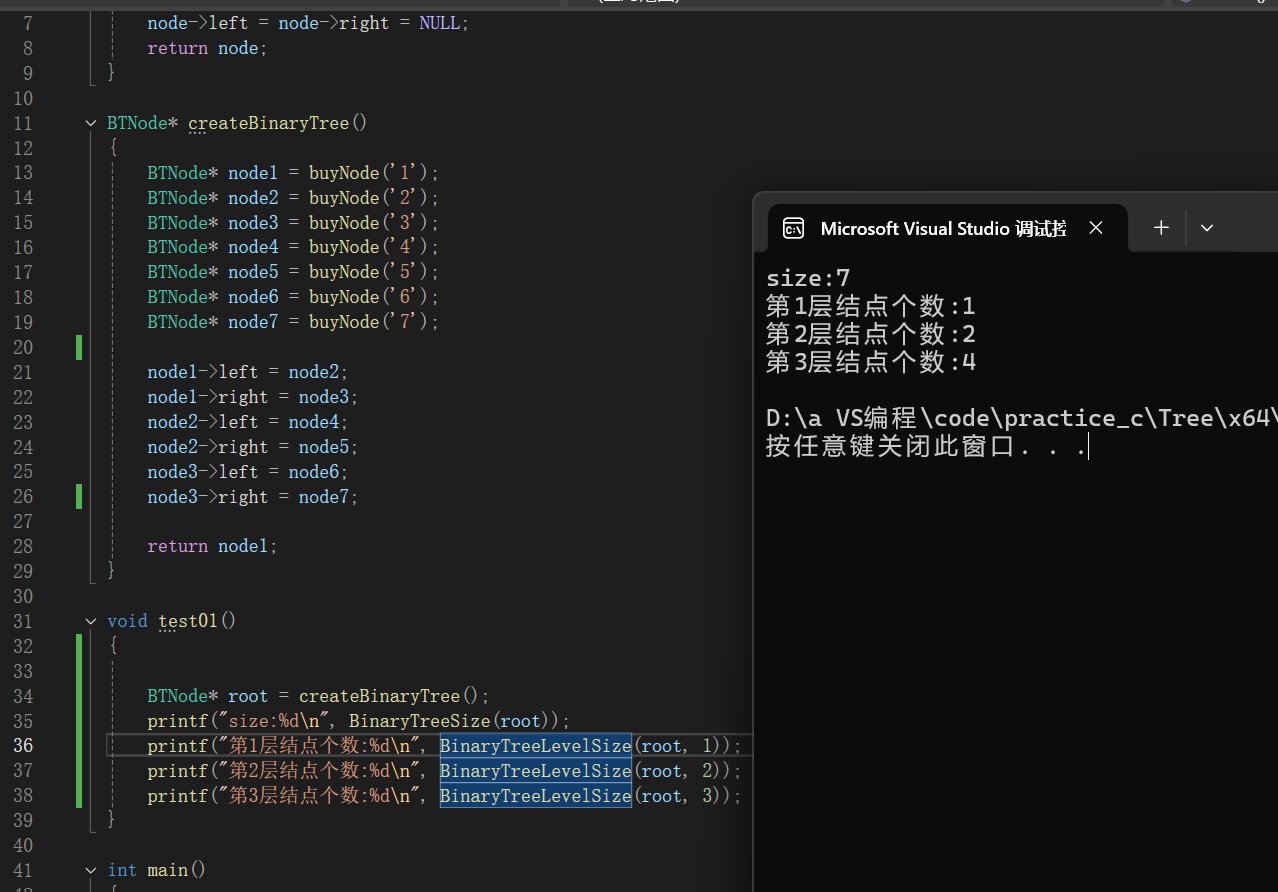
int BinaryTreeLevelSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelSize(root->left, k - 1) + BinaryTreeLevelSize(root->right, k - 1);
}
2.6二叉樹的深度
深度 = 根結點 + max(左子樹的深度+右子樹的深度)
//二叉樹的深度
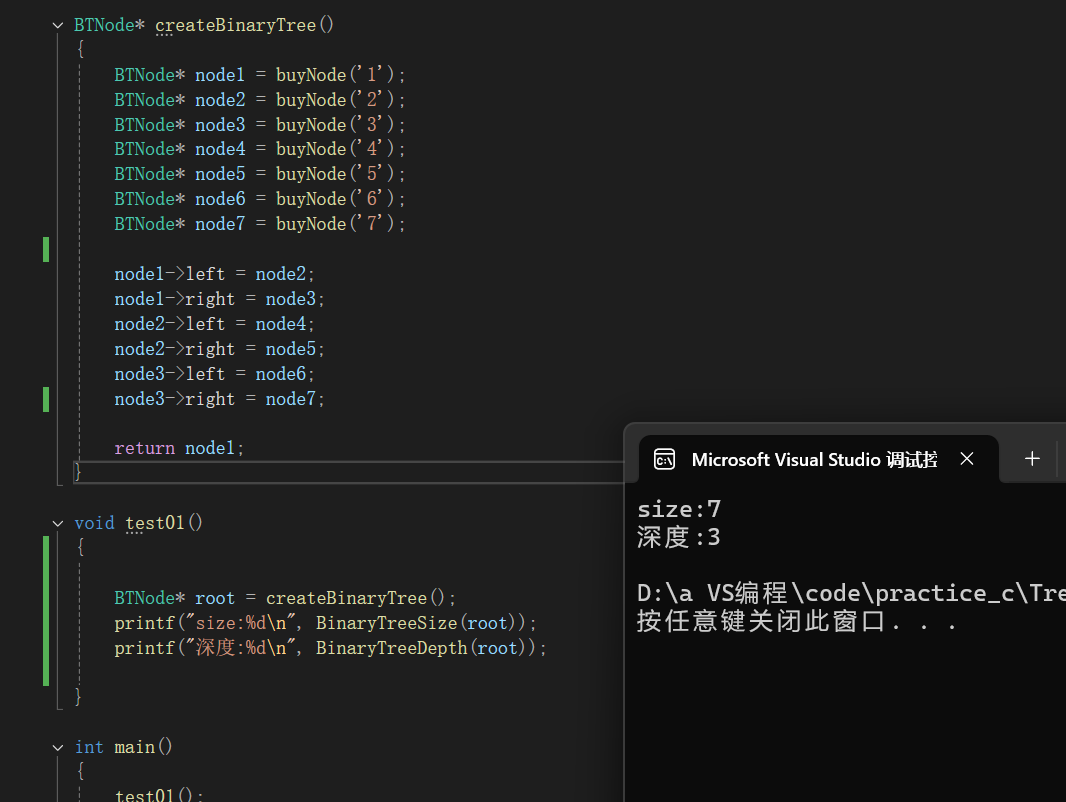
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}return 1 + max(BinaryTreeDepth(root->left), BinaryTreeDepth(root->right));//return 1 + (BinaryTreeDepth(root->left) > BinaryTreeDepth(root->right) ? BinaryTreeDepth(root->left) : BinaryTreeDepth(root->right));
}
2.7二叉樹查找值為x的結點
//二叉樹查找值為x的結點
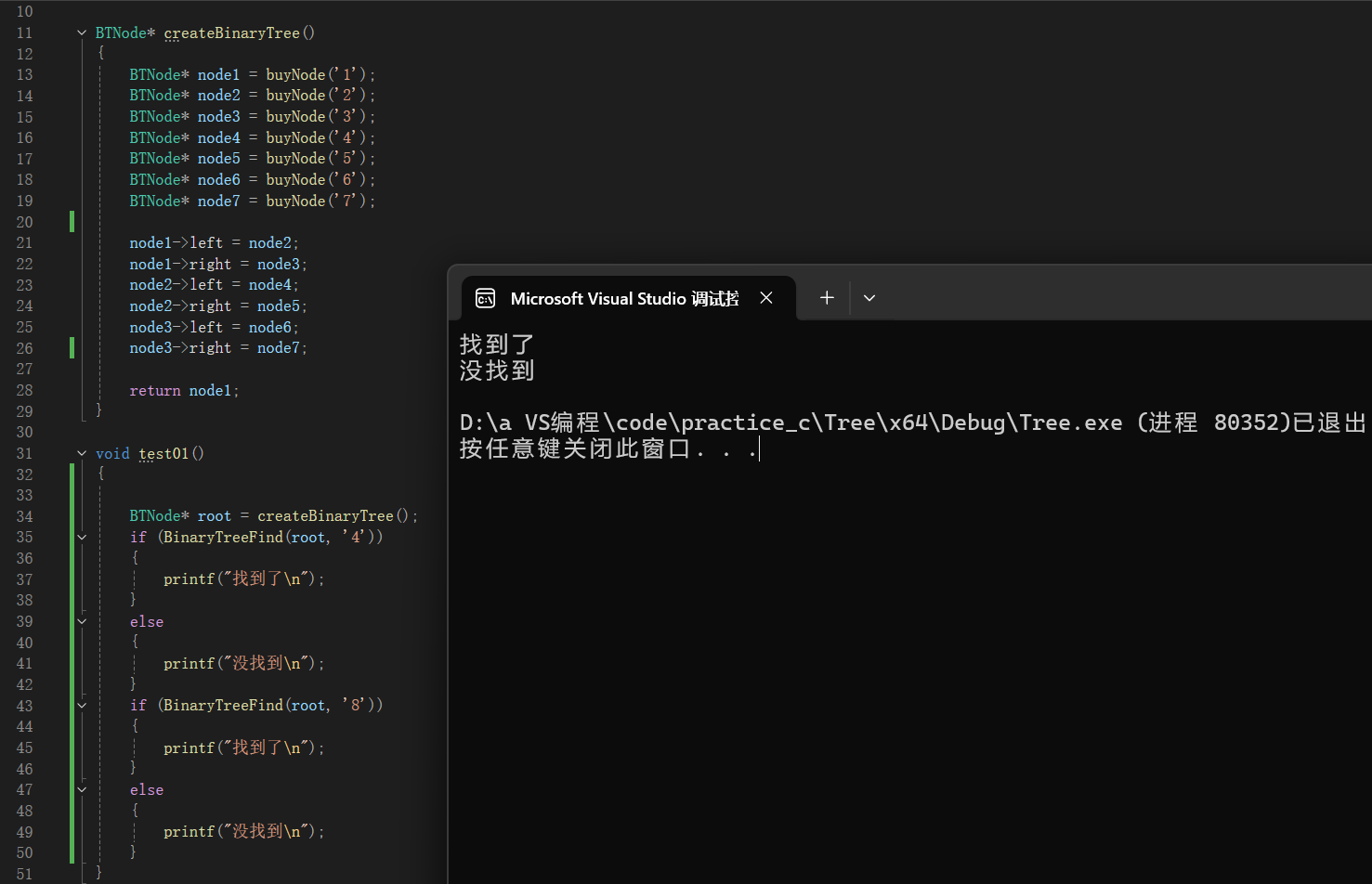
BTNode* BinaryTreeFind(BTNode* root, BTDtatatype x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode*leftFind = BinaryTreeFind(root->left, x);if (leftFind){return leftFind;}BTNode*rightFind = BinaryTreeFind(root->right, x);if (rightFind){return rightFind;}
}
2.8二叉樹的銷毀
//二叉樹的銷毀
void BinaryTreeDestroy(BTNode** root)
{if (root == NULL){return;}BinaryTreeDestroy(&((*root)->left));BinaryTreeDestroy(&((*root)->right));free(*root);*root = NULL;
}二叉樹的層序遍歷
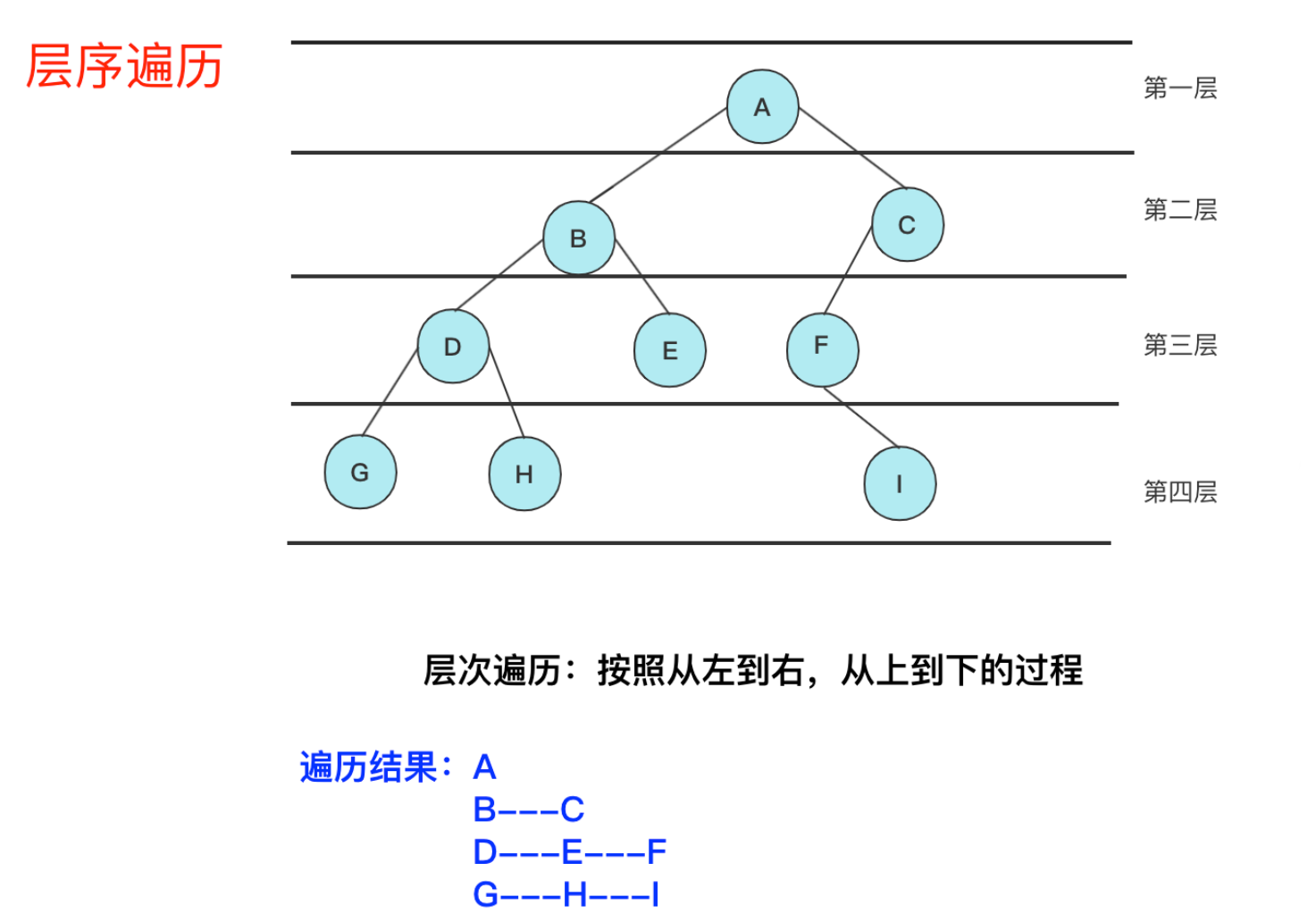
借助數據結構--隊列
首先將之前所編寫過的隊列的.h和.c文件導入進來
注意:
1.要包含隊列的頭文件
2.修改隊列的頭文件:修改隊列的保存類型,務必要加struct,為了告訴編譯器BinaryTreeNode是個結構體。
2.9層序編列實現:
//層序遍歷
void levelOrder(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){//取隊頭,出隊頭BTNode*top = QueueFront(&q);QueuePop(&q);printf("%c ", top->data);//將左右孩子入隊列if (top->left)QueuePush(&q, top->left);if (top->right)QueuePush(&q, top->right);}QueueDestrory(&q);
}
2.10判斷是否為完全二叉樹
前置知識:完全二叉樹的特點:
1)最后一層節點個數不一定達到最大
2)結點從左到右依次排列
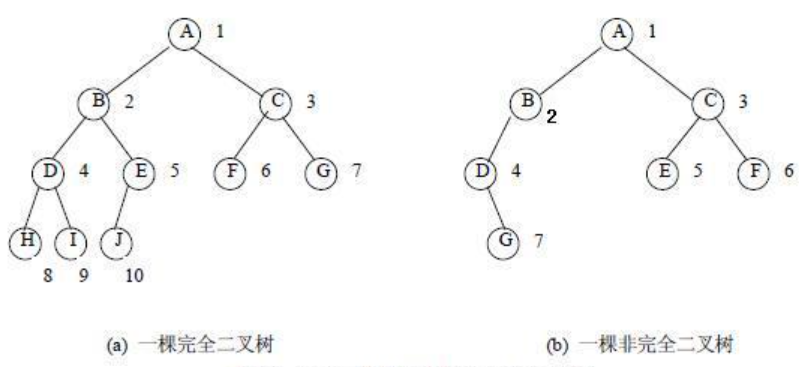
與二叉樹的層序遍歷相同,借助隊列進行實現:
在第一個循環中,取隊頭,出對頭,直到遇到第一個空結點出循環,并進入到第二個循環。
若在第二個循環中,從非空隊列中取到了非空的隊頭結點,那么該二叉樹一定不是完全二叉樹,否則一定是完全二文樹
//判斷是否為完全二叉樹
bool BinaryTreeComlete(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){//取隊頭,出隊頭BTNode* top = QueueFront(&q);QueuePop(&q);if (top == NULL){break;}QueuePush(&q, top->left);QueuePush(&q, top->right);}//隊列不一定為空while(!QueueEmpty(&q)){BTNode* top = QueueFront(&q);QueuePop(&q);if (top != NULL){return false;}}QueueDestrory(&q);return true;
}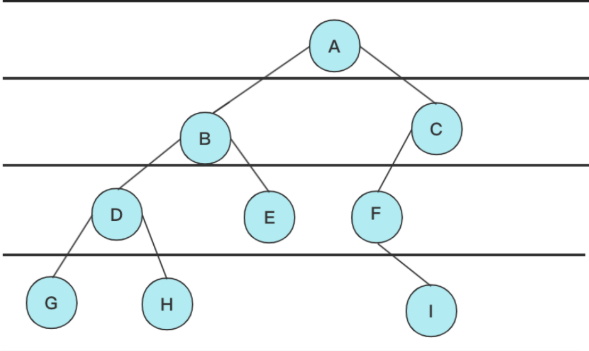
以上圖做例子,應不是完全二叉樹:符合預期
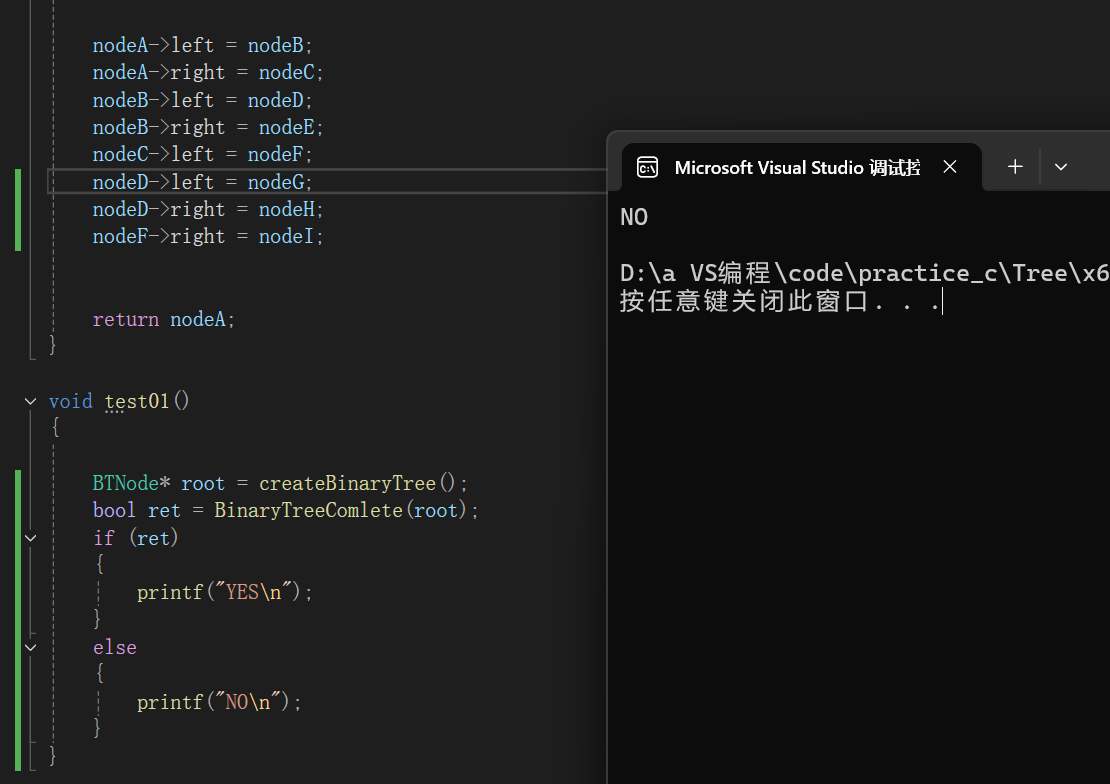
把G H I結點去掉后應為完全二叉樹:符合預期
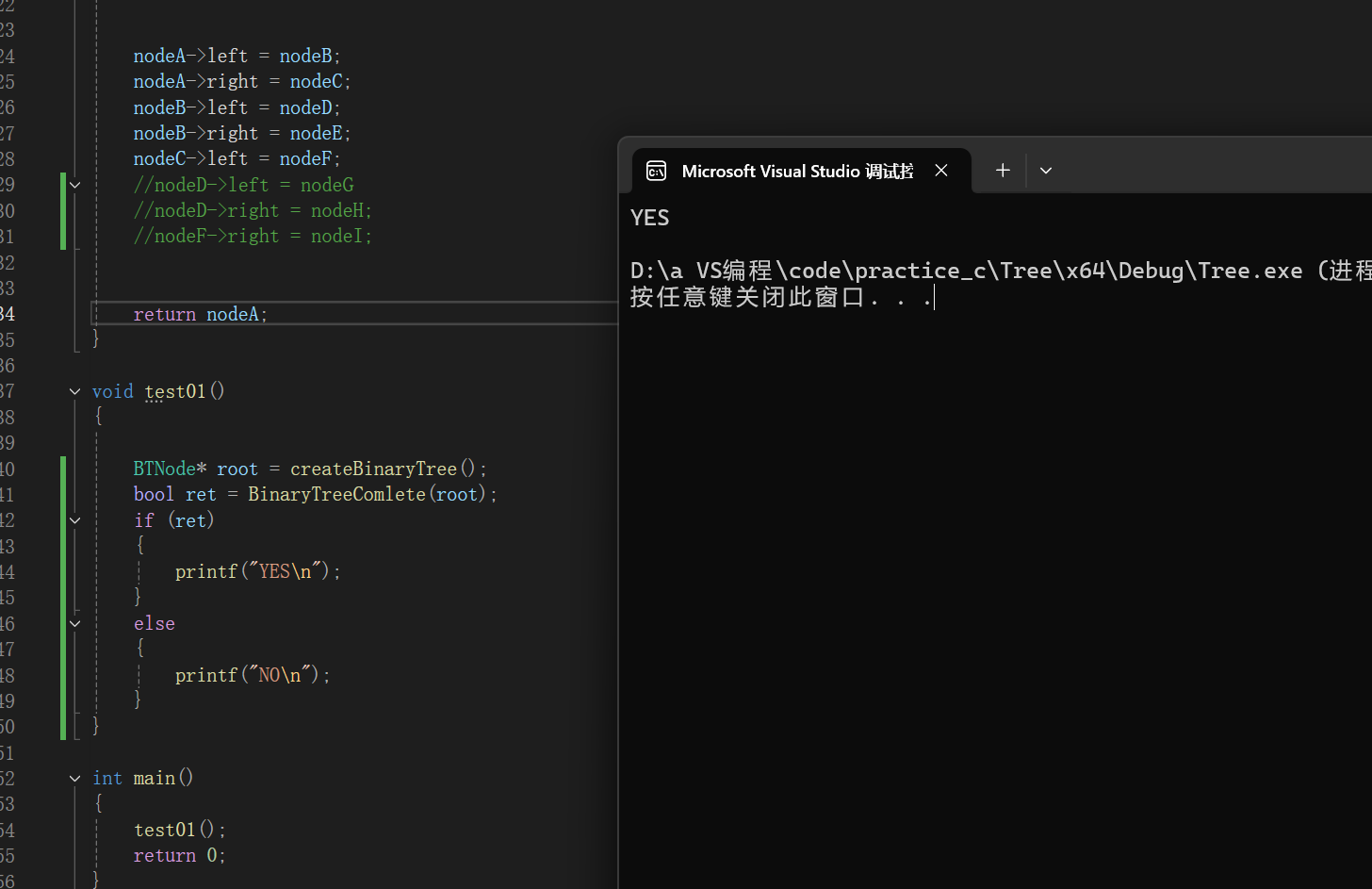

-介紹)

 --配置使用RabbitMQ)








)


)



