計算機網絡第3章（上）：數據鏈路層全解析—

一、數據鏈路層的功能
二、組幀
- 2.1 字符計數法（Character Count）
- 2.2 字符填充法（Character Stuffing）
- 2.3 零比特填充法
- 2.4 違規編碼法
三、差錯控制
- 3.1 檢錯編碼（奇偶校驗碼）
- 3.2 循環冗余校驗（Cyclic Redundancy Check， CRC）
- 3.3 海明校驗碼（Hamming Code）
四、流量控制與可靠傳輸
- 4.1 滑動窗口機制
- 4.2 停止-等待協議（S-W）
- 4.3 后退N幀協議（GBN）
- 4.4 選擇重傳協議（SR）
- 4.5 三種協議的信道利用率分析

一、數據鏈路層的功能

數據鏈路層使用物理層提供的 "比特傳輸" 服務
數據鏈路層 為 網絡層 提供服務，將網絡層的 IP 數據報（分組）封裝成幀，傳輸給下一個相鄰結點
物理鏈路： 傳輸介質(0層)+物理層(1層) 實現了相鄰結點之間的 "物理鏈路"

物理鏈路確實包含兩個部分，但更準確的表述是：傳輸介質（第0層，物理介質層）：前面講到過的電纜（雙絞線、同軸電纜）、光纖、無線信道等，負責實際承載信號（電信號、光信號、電磁波）；物理層（第1層，協議層）：定義如何在介質上傳輸原始比特流，包括：信號編碼（如曼徹斯特編碼）、調制解調、時鐘同步等。關鍵區別：傳輸介質是物理實體（如網線），物理層是協議規范（如以太網 100BASE-TX 標準），兩者共同實現 "比特傳輸" 服務，但屬于不同抽象層次。

邏輯鏈路：數據鏈路層需要基于 "物理鏈路"，實現相鄰結點之間邏輯上無差錯的 "數據鏈路(邏輯鏈路)"

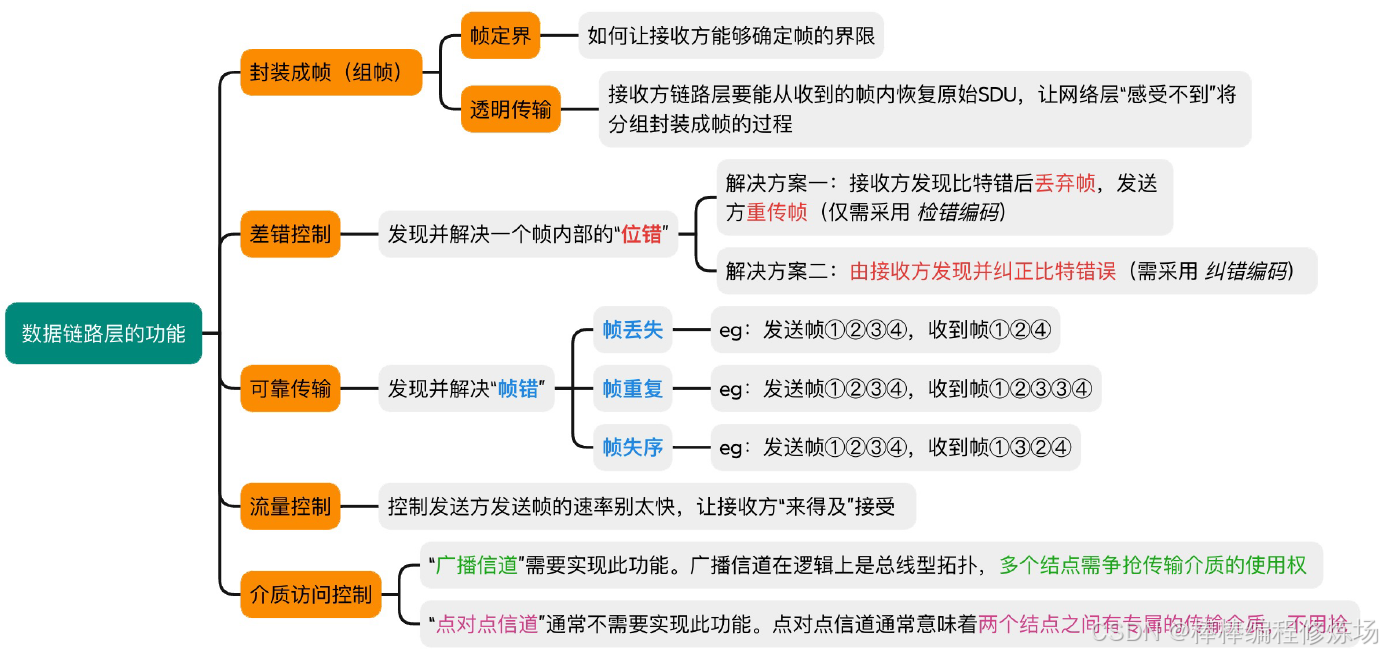
數據鏈路的功能： 第3章主要圍繞數據鏈路的功能進行講解(逐個拆解細分)

過程分解（發送端）示例：

# 數據鏈路層構造好一個幀（以字節為單位）
10101010 10101010 10101010 ... （字節序列）# 物理層將字節拆成比特流
1 0 1 0 1 0 1 0 ...  ← bit stream# 物理層使用編碼方案將比特轉為信號波形
| 編碼方案                    | 特點                |
| ----------------------- | ----------------- |
| NRZ（Non-Return-to-Zero） | 高電平=1，低電平=0       |
| 曼徹斯特編碼                  | 一個比特周期中有電平翻轉，用于同步 |
| 4B/5B 編碼 + NRZI         | 增強同步性和誤碼檢測能力      |
| 8B/10B 編碼               | PCIe、USB、光纖通信中常用  |

二、組幀

由于物理層是無結構的比特流傳輸（bit stream），沒有幀的概念，接收方無法知道什么時候是一個數據包的開始和結束。因此需要數據鏈路層將數據 "打包成幀"，并定義好幀邊界、起止、檢測錯誤等功能。數據鏈路層通常通過以下幾種方式實現幀的起止識別：

2.1 字符計數法（Character Count）

原理： 幀的第一個字段指明整個幀中字符的個數（即幀的總長度），接收方根據這個計數值提取出整個幀
優點： 實現簡單，效率較高（無額外的比特填充或轉義）
缺點： 如果計數字段本身出錯，將導致整個幀的邊界錯亂（幀同步丟失），后續數據可能無法正確識別
最大缺點： 任何一個計數字段出錯，都會導致后續所有幀無法定界

場景： 連續發送三幀（字符計數法）

幀1: 長度 4 + 數據（共4字節）00000100 10100001 11110000 00001111
幀2: 長度 3 + 數據（共3字節）00000011 11001100 10101010
幀3: 長度 2 + 數據（共2字節）00000010 11110011# 幀1長度出錯（由4變為6）
00000110 10100001 11110000 00001111 00000011 11001100 10101010 00000010 11110011
# 字節序列（標號）如下: 
| 字節號 | 值        | 備注                 |
| --- | -------- | ------------------ |
| 1   | 00000110 | 錯誤的幀1長度（6）         |
| 2   | 10100001 | 幀1數據1              |
| 3   | 11110000 | 幀1數據2              |
| 4   | 00001111 | 幀1數據3              |
.....一步錯后面的都錯位了......
| 5   | 00000011 | 幀1數據4（原為幀2頭）  ---錯位     |
| 6   | 11001100 | 幀1數據5（原為幀2數據） ---錯位     |
| 7   | 10101010 | 開始解析下一幀的"長度"字節（錯位） |
..........

2.2 字符填充法（Character Stuffing）

原理： 使用特殊字符表示幀的起始和結束，例如 FLAG = DLE STX … DLE ETX，如果幀數據中出現了這些特殊字符，為避免誤解，使用轉義字符（如 DLE）進行轉義處理
優點： 可以較好處理幀邊界識別問題，相比位填充，適用于基于字符的通信系統（如串口通信）
缺點： 只適用于字符流傳輸（不是比特流），幀內字符一多，轉義開銷較高

SOH（Start of Header）和 EOT（End of Transmission）也確實出現在一些組幀或通信協議中，它們和你前面看到的 STX/ETX 類似，屬于字符填充法（即 "基于控制字符的組幀"），它們是 ASCII 控制字符中的一部分，常用于早期串口通信、串行線路或面向字符的協議中，比如 XMODEM、ZMODEM、早期串行打印通信等：

控制字符	十六進制	意義
SOH	0x01	Start of Header（報頭開始）
STX	0x02	Start of Text（正文開始）
ETX	0x03	End of Text（正文結束）
EOT	0x04	End of Transmission（傳輸結束）
DLE	0x10	Data Link Escape（數據鏈路轉義）

在字符填充法中，這些控制字符用于標識幀邊界或數據部分的結構，例如：

# 常見用法一: SOH + 數據 + EOT
# 這種格式有時用于: 一幀一個包，簡單可靠，傳輸完一幀就用 EOT 表明傳輸完畢
SOH（0x01） 表示幀或報頭開始
EOT（0x04） 表示整個傳輸的結束# 常見用法二: SOH + 報文頭 + STX + 數據 + ETX + EOT
SOH 開始整個幀
STX 開始正文（正文與報頭之間分隔）
ETX 正文結束
EOT 整個傳輸完畢[SOH][幀頭][STX][正文數據][ETX][校驗][EOT]

字節填充法圖示1：

字節填充法圖示2：

字節填充法圖示3：

你看到的 "字符填充" 其實可以叫 "字節填充"，在早期的通信協議中，字符（character）= 字節（byte），因為一個字符就是一個字節（8位），例如 ASCII 編碼，所以："字符填充法" = "字節填充法"（在指 8 位字符編碼時，是一回事），在使用 ASCII 的協議中，SOH、EOT、ESC 等這些控制字符都是一個字節，所以我們加一個 ESC，就是加了一個字節 —— 所以叫 "字節填充" 也沒錯。"字符填充" 突出的是在字符流中插入特殊字符（如 FLAG、ESC、DLE），早期通信設備用的是字符終端（Character-oriented protocols），所以強調 "在字符層級做填充"。舉個例子：

協議類型	填充術語常見寫法
HDLC（比特協議）	比特填充
PPP、SLIP（字符協議）	字符填充 / 字節填充

現代協議中為什么偏向說 "字節填充"？因為現代通信系統中：不再以 "字符" 為核心單位（Unicode 一個字符 ≠ 一個字節），網絡傳輸的單位是字節（byte stream），所以更技術中立、準確的說法是：字節填充（byte stuffing）。

2.3 零比特填充法

原理： 用特定的比特模式來標識一幀的開始和結束，比如 HDLC 使用 01111110。若數據中出現5個連續的 1 比特，發送方自動插入一個 0（填充），接收方在收到5個連續的 1 后發現第6位是 0，就將其刪除，從而恢復原始數據。示例：

原始數據中包含：01111110
則實際發送為：011111010

接收方解析后將填充的 0 去掉，優點： 適用于位導向協議，可用于任意二進制數據，缺點： 實現稍復雜（需要逐位判斷和填充）。
圖例1：

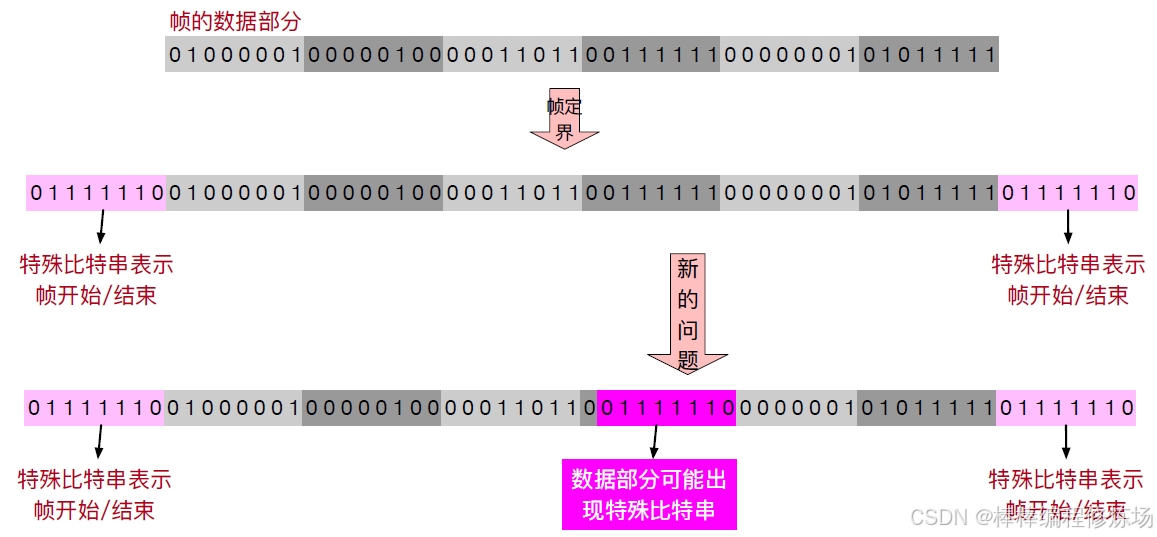
圖例2：

2.4 違規編碼法

原理： 某些物理層編碼規則中存在非法的比特模式（正常傳輸中不會出現），數據鏈路層使用這些非法模式作為幀的起止標志。示例： 例如在曼徹斯特編碼中，若某個比特組合違反電壓跳變規則，則認為是幀邊界。優點： 不需要增加額外的開銷，可在物理層檢測幀邊界，效率高。缺點： 依賴于物理層的具體實現，不具備通用性。

知識回顧與重要考點：

三、差錯控制

數據鏈路層的差錯控制功能

3.1 檢錯編碼（奇偶校驗碼）

奇偶校驗（Parity Check）是一種簡單的檢錯編碼技術，用于在數據鏈路層中檢測傳輸過程中發生的1位錯誤（bit error）。它的基本思想是：在原始數據后添加一個額外的比特（稱為奇偶校驗位），使得整個數據的1的個數符合 "奇數" 或 "偶數" 的要求。奇偶校驗的兩種類型：

奇校驗碼： 整個校驗碼（有效信息位和校驗位）中 "1" 的個數為奇數
偶校驗碼： 整個校驗碼（有效信息位和校驗位）中 "1" 的個數為偶數

【例】給出兩個編碼 1001101 和 1010111 的奇校驗碼和偶校驗碼。設最高位為校驗位，余7位是信息位，則對應的奇偶校驗碼為：

校驗碼是否一定要放在數據末尾？能不能放在最前面？可以放最前面，也可以放最后，甚至中間都可以，但通常放在末尾（例子放在開頭）。這是協議約定問題，不是技術限制。校驗位的位置沒有本質上的 "必須"，關鍵在于發送方和接收方達成一致。但通常放在末尾的原因是：① 數據生成后，再計算校驗位比較自然（邏輯清晰）② 接收方收到數據后，只要讀完整體，再判斷是否符合校驗規則 ③ 與 CRC、FCS 等其他編碼方式習慣保持一致。

奇偶校驗碼的生成與判斷可以通過非常簡單的數字電路（邏輯門）實現，尤其是：偶校驗 = 所有比特的異或和，即：

data[0] ⊕ data[1] ⊕ data[2] ⊕ ... ⊕ data[n-1]
# 結果是: 
# 0 → 偶數個1(滿足偶校驗)
# 1 → 奇數個1(不滿足偶校驗)# ⊕: 異或（模2加）
0 ⊕ 0  =  0 
0 ⊕ 1  =  1 
1 ⊕ 0  =  1 
1 ⊕ 1  =  0  # 兩比特相"異" 時，結果為1# 偶校驗: 01001101 11010111
# 求偶校驗位: 
# 1001101 ==》 經過計算得0，所以前面寫0 ==》01001101
1 ⊕ 0 ⊕ 0 ⊕ 1 ⊕ 1 ⊕ 0 ⊕ 1 = 0 
# 1010111 ==》 經過計算得1，所以前面寫1 ==》11010111
1 ⊕ 0 ⊕ 1 ⊕ 0 ⊕ 1 ⊕ 1 ⊕ 1 = 1# 進行偶校驗(所有位進行異或，若結果為1說明出錯): 
0 ⊕ 1 ⊕ 0 ⊕ 0 ⊕ 1 ⊕ 1 ⊕ 0 ⊕ 1 = 0  # 正確
# 假設最后一位由1變成了0，則計算結果為1，可以發現出錯
1 ⊕ 1 ⊕ 0 ⊕ 1 ⊕ 0 ⊕ 1 ⊕ 1 ⊕ 0 = 1 # 出錯
# 可以發現最后兩位都由1變成了0，但是計算結果仍然是0，所以: 
# 無法檢測出偶數位錯誤
1 ⊕ 1 ⊕ 0 ⊕ 1 ⊕ 0 ⊕ 1 ⊕ 0 ⊕ 0 = 0

奇偶校驗的作用和局限性：

優點： 實現簡單，計算開銷非常小（硬件中1個異或門就能實現），可以檢測單個比特錯誤

缺點：

缺陷點	說明
檢測能力弱	只能檢測奇數個錯誤（如 1、3、5 位錯），偶數位錯誤無法檢測
無法糾錯	它只能 `"發現"` 錯誤，不能 `"修正"` 錯誤的位置或內容
不能應對高誤碼環境	在噪聲嚴重的物理環境中效果較差

奇偶校驗碼常用于以下低速或對可靠性要求不高的場景：

老式串口通信（如 RS-232）
內存 ECC 簡化模式
早期網絡協議（如 HDLC、PPP）中可作為第一道錯誤檢測

知識回顧：

3.2 循環冗余校驗（Cyclic Redundancy Check， CRC）

本小節總覽：

CRC 的基本思想是： 把整個數據當成一個 "二進制多項式"，然后用另一個 "預先約定好的多項式" 去做除法，取余數作為 "校驗碼" 加在數據末尾，接收方再除一次，如果余數不為0，就說明出錯了。這就像你寄快遞時在包裹外面貼了個驗收碼，收件人用規則檢查發現對不上，就知道途中被調包/損壞了。

要通俗理解 CRC，需要掌握幾個核心概念：

數據看成多項式， 假設你要發送的數據是這樣一個 8 位二進制串：10110011，我們把它視為一個 "多項式"，例如：
```
1·x? + 0·x? + 1·x? + 1·x? + 0·x3 + 0·x2 + 1·x1 + 1·x?
# 即為: 
x? + x? + x? + x1 + x?
```
這個就叫 數據多項式
生成多項式（G(x)）是事先約定好的 "除數"，發送方和接收方都要提前約定一個 "生成多項式"，例如：
```
G(x) = x3 + x + 1 ? 對應二進制是: 1011
# 1 * x3 + 0·x2 + 1·x1 +  1·x?	
```
這個多項式的位數 = 校驗碼的位數 + 1，所以這個 G(x) 的校驗碼長度是：3位

具體的 CRC 編碼過程：

# ? 第一步: 數據后補 0
# 既然你打算生成一個3位校驗碼，就在數據后面補上3個0
# 原數據: 10110011  
# 補零后: 10110011000   ← 11位# ? 第二步: 用 G(x) 做二進制除法
# 對 10110011000 用生成多項式 1011 做二進制除法（注意這里的除法不是普通的除法，而是用 異或（XOR） 來代替減法）:
# 只要會 "豎式除法" 和 "異或運算" 就能算 CRC
# 核心規則是: 
# 每次從高位開始，如果被除數的首位是1，就把 G(x) 對齊后異或,否則跳過這一位
# 最終余數就是 CRC 校驗碼# 舉個直覺化的比喻: 
# 它就像你用尺子劃過一段木板，哪塊凸出來（1）就削一下（異或），平了就跳過
# 最后 "削剩下的" 就是校驗碼# ? 第三步: 把"余數"加在原始數據后面，假設你除完之后的余數是 101
# 那么最終發送的數據就是: 
# 10110011 101
這就是完整的 "數據幀 + CRC校驗碼"# 接收方做什么？
# 收到后，接收方也用同樣的生成多項式 1011 去除整段 10110011101
# 如果結果 沒有余數（即余數為 0） → 數據無誤
# 否則說明數據在傳輸中出錯了

這樣可能不太好理解，我們結合圖示來理解每一個步驟：設生成多項式為 G(x)=x³+x²+1，信息碼為 101001，求對應的 CRC 碼：

確定 K、R 以及生成多項式對應的二進制碼。K = 信息碼的長度 = 6，多項式對應二進制碼為：1011，4 位，減去 1，則 R = 3（也可以直接取生成多項式的最高次冪 3），總位數：N = K + R = 9
信息碼為 101001，且 R = 3，則補 0 后的數據為：101001000
對補 0 后的數據用生成多項式進行模 2 除法，產生余數
則對應的 CRC 碼為：001，完整發送的數據：101001001
檢錯和糾錯：

總結口訣： CRC 除法就像長除法，只是每次減法用的是異或！CRC 碼有些表示的是單獨的校驗位，不包括原始數據，有些又會把原始數據算上，這個只要你知道在說什么就好了，具體情況具體分析。----- 本小節我也混用了，不管了

拓展： 實際中，CRC 一般不用于糾錯，而是用于 錯誤檢測，所以下面的了解一下即可。

3.3 海明校驗碼（Hamming Code）

Richard Hamming 演講選段：早年，我在攻克一個又一個難題，成功的多，失敗的少。可是，周五解決了一個問題回到家里后，我卻并不快活，反而很沮喪。我看到生活就是一個問題接著一個問題又接著另一個問題。想了相當長一陣子后，我決定以另一種方式干活：你的工作要成為別人工作的基石！于是別人就會說： "看哪，我站在他的肩膀之上，我看得更遠了"。科學的本質是積累！我再也不去做相互孤立的問題，除非它能代表某一類問題的共性。我決不再去解決單一的問題。你要么讓人們在你的成果上有所建樹，要么別人不得不把你干的活從頭再來復制一遍。

當你通過網絡/通信線路發送數據時，可能某一位會出錯。普通奇偶校驗只能檢測是否有錯誤，但不能定位是哪一位錯了，更不能修復它。海明碼的目標是： 能發現 1 位錯誤，能準確定位是哪一位錯，并自動糾正。一句話理解： 海明碼是一種能檢測并糾正1位錯誤的糾錯碼，通過插入特定的校驗位，使得每一位錯誤都能被唯一定位。海明碼的基本原理： 插入若干校驗位，使得每一位都有唯一 "被誰檢查" 的組合，把數據分布在一個比原始數據長的 "碼字" 中，每個校驗位負責檢查若干位（包括它自己或不包括）。

需要多少校驗位？

海明碼求解步驟：
① 確定校驗位數量：

② 確定校驗位的分布：

③ 求校驗位的值：

④ 檢查糾錯：

⑤ 最后結果：

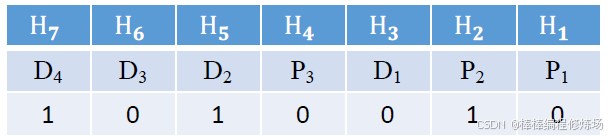
海明碼求解步驟-格式變化：

拓展：

知識回顧：

四、流量控制與可靠傳輸

4.1 滑動窗口機制

滑動窗口機制是一種用于 提高鏈路利用率、實現流量控制 和 保證可靠傳輸 的方法，廣泛應用于 數據鏈路層（如 HDLC 協議） 和 傳輸層（如 TCP）

發送窗口（Send Window）：發送窗口是發送方維護的一個連續的幀編號區間，它表示當前允許發送但尚未被確認的數據幀范圍。窗口大小（N）： 可以同時發送的最大未確認幀數。起點： 最早發送但未確認的幀。終點： 起點 + N - 1。如果窗口滿了（即未確認的幀數量等于窗口大小），則發送方暫停發送，直到收到確認（ACK）后窗口向前滑動。

接收窗口（Receive Window）： 接收窗口是接收方維護的一個幀編號區間，表示其當前準備好接收的數據幀范圍，一般與發送窗口同樣大小（但不一定），接收到正確的幀后會向前滑動，并發送確認。

重點關注四個方面：

4.2 停止-等待協議（S-W）

要點總覽：

停止-等待協議：

數據幀、確認幀、幀序號的概念：

正常情況示例：

異常情況示例：數據幀丟失

異常情況示例：確認幀丟失

為什么一定要給幀編號？

區分重復幀和新幀： 由于網絡可能出現丟包或延遲，發送方可能因為沒收到確認而重發上一幀。接收方通過幀編號可以判斷收到的幀是新的還是之前已經接收過的重復幀。如果接收方收到的幀編號和上一次接收的幀編號相同，就說明這是重發的重復幀，應丟棄。如果幀編號不同，說明是新幀，可以接收并發送確認
保證數據的順序和完整性： 幀編號幫助接收方確保數據按正確順序接收，不會錯亂或重復

防止確認丟失帶來的誤解： 如果確認幀（ACK）丟失，發送方會重發上一幀。沒有幀編號，接收方無法判斷這是重復幀還是新幀，會導致數據混亂。幀編號解決了這個問題

簡單舉例（文字）：

發送方發送幀0，等待確認
接收方收到幀0，處理并回復ACK0
發送方沒收到ACK0，重發幀0
接收方收到幀0，但它已經處理過了，通過編號知道這是重復幀，丟棄并重新發送ACK0
發送方收到ACK0后，發送幀1

異常情況示例：數據幀有差錯

知識回顧：

4.3 后退N幀協議（GBN）

要點總覽：

后退N幀協議(Go-Back-N Protocol，簡稱 GBN)： 是數據鏈路層的一種重要滑動窗口協議，用于實現可靠數據傳輸。后退N幀協議是一種基于滑動窗口的 ARQ(自動重傳請求) 協議，它允許發送方在收到確認前連續發送多個幀，從而提高信道利用率。核心特點：

發送窗口大于1： 可以連續發送多個幀而無需等待確認
累積確認： 接收方只需對按序到達的最后一個正確幀進行確認
出錯時后退N幀： 當某個幀出錯時，發送方需要重傳該幀及其后所有已發送但未確認的幀

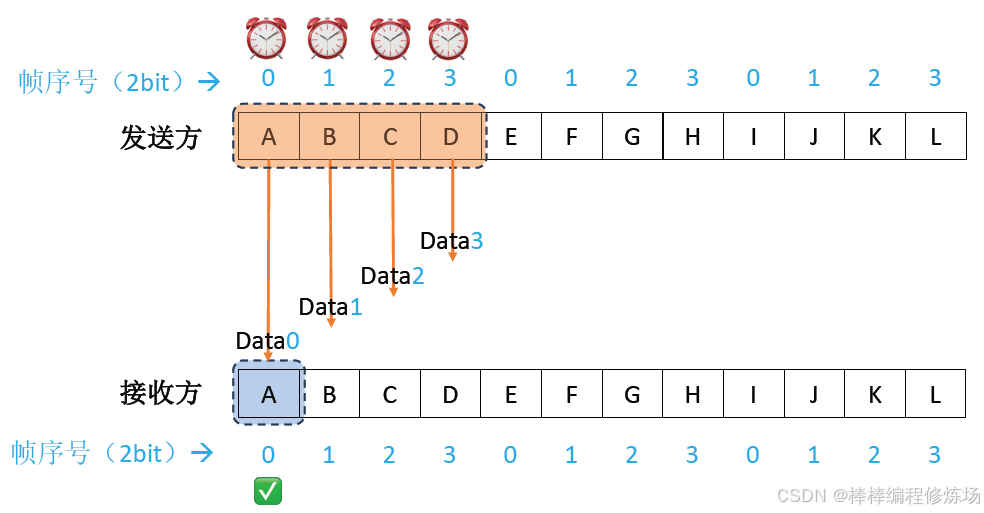
正常情況示例：

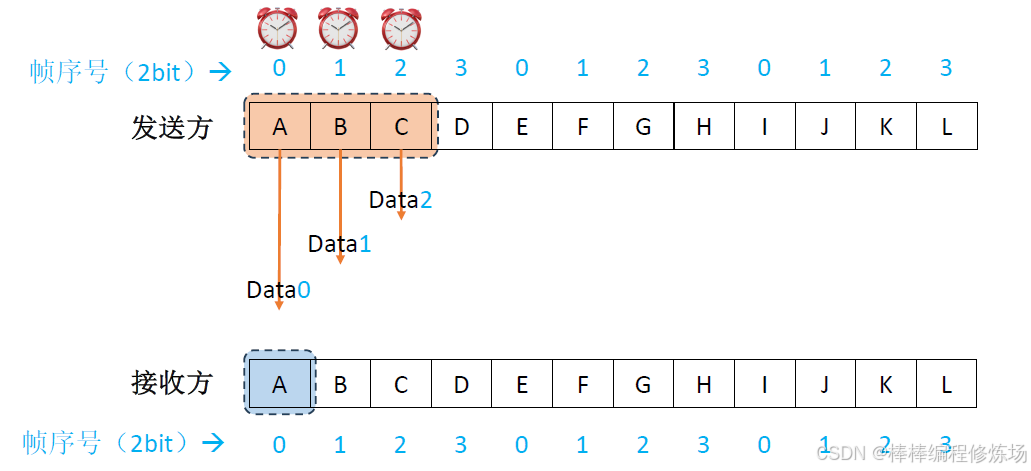
異常情況示例：數據幀丟失

異常情況示例：確認幀丟失

探討：如果不滿足 W_T + W_R ≤ 2ⁿ 會有什么問題？

知識回顧：

4.4 選擇重傳協議（SR）

要點總覽：

選擇重傳協議(Selective Repeat Protocol，簡稱 SR) 是數據鏈路層另一種重要的滑動窗口協議，它通過選擇性重傳提高了信道利用率。選擇重傳協議是一種改進的 ARQ 協議，它只重傳真正丟失或損壞的幀，而不是像 GBN 那樣重傳所有未確認幀。核心特點：

發送窗口和接收窗口都大于1： 可以緩存多個幀
獨立確認： 每個正確接收的幀都會被單獨確認
選擇性重傳： 只重傳真正丟失或損壞的幀
亂序接收： 可以接收并緩存亂序但正確的幀

選擇重傳協議的窗口大小限制條件：

正常情況示例：

異常情況示例：數據幀丟失

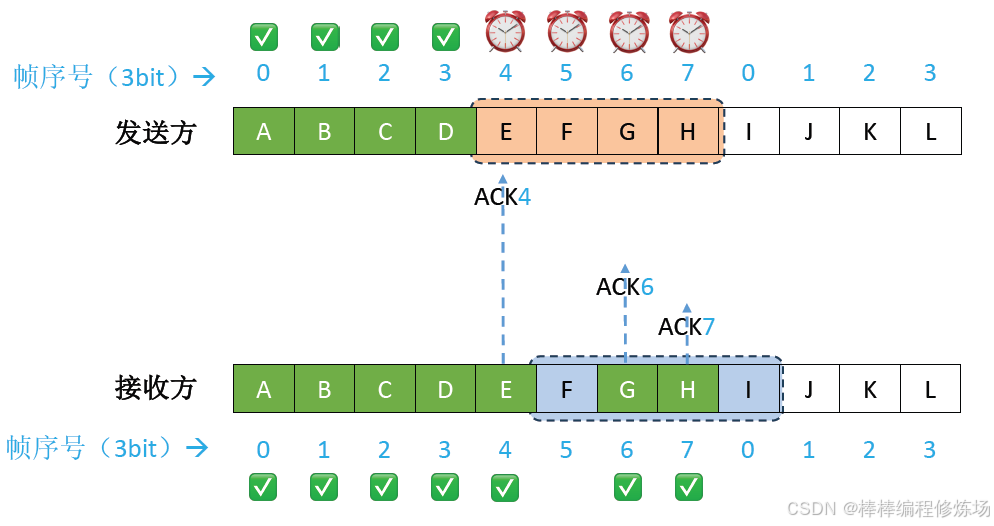
異常情況示例：數據幀因差錯而被丟失

異常情況示例：確認幀丟失

探討：如果不滿足 W_T + W_R ≤ 2ⁿ 會有什么問題？

知識回顧與重要考點：

4.5 三種協議的信道利用率分析

知識總覽：

S-W 協議的信道利用率：

例題：2018真題_36

GBN、SR 協議的信道利用率：

例題：2014真題_36

例題：2015真題_35

術語補充：滑動窗口協議

術語補充：ARQ 協議、連續 ARQ 協議

知識回顧

本文為個人學習記錄與復習整理之用，旨在幫助自己系統鞏固計算機網絡相關知識，同時也希望能為正在學習該領域的同學提供一些參考與幫助。部分內容參考了公開課資料、他人學習筆記或網絡公開資源，其中部分圖片或示意圖來自網絡，僅用于非商業性質的學習交流。如有侵權或不當引用之處，敬請聯系我刪除或更正。
在這里插入圖片描述

????好書不厭讀百回，熟讀課思子自知。而我想要成為全場最靚的仔，就必須堅持通過學習來獲取更多知識，用知識改變命運，用博客見證成長，用行動證明我在努力。
????如果我的博客對你有幫助、如果你喜歡我的博客內容，請 點贊、評論、收藏 一鍵三連哦！聽說點贊的人運氣不會太差，每一天都會元氣滿滿呦！如果實在要白嫖的話，那祝你開心每一天，歡迎常來我博客看看。
?編碼不易，大家的支持就是我堅持下去的動力。點贊后不要忘了 關注 我哦！