一、題目解析
?
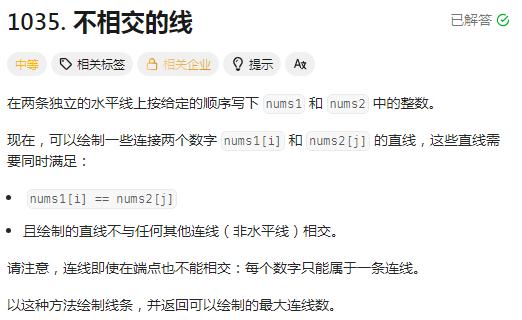
?光看題目要求和例圖，感覺這題好麻煩，直線不能相交啊，每個數字只屬于一條連線啊等等，但我們結合題目所給的信息和例圖的內容，這不就是最長公共子序列嗎？，我們把最長公共子序列連線起來，符合該題要求，由于每個數字只能連一條線，所以這里的公共子序列長度等于不相交的線的條數
二、算法原理
這里詳細內容移步我之前的博客動態規劃-1143.最長公共子序列-力扣(LeetCode)_lintcode 最長公共子序列-CSDN博客
1、狀態表示
dp[i][j]表示：在[0，i]的nums1和[0，j]的nums2所有子序列中最長的公共子序列
2、狀態轉移方程
根據兩個數組最后一個元素劃分狀態?
dp[i][j]->nums1[i]==nums2[j]->dp[i-1][j-1]+1
? ? ? ? ?->nums[i]!=nums2[j]->dp[i-1][j]
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?->dp[i][j-1]
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?->dp[i-1][j-1]
由于前兩個都包括第三種狀態，所以max(dp[i-1][j],dp[i][j-1])
3、初始化
最壞情況為沒有最長子序列，所以全初始化為0，且多加一行一列用于初始化，注意下標映射
4、填表順序
從上往下，從左往右
5、返回值
dp[m][n]，m為nums1的長度，n為nums2的長度
建議對最長公共子序列有遺忘的，可以回顧我之前的博客
鏈接：動態規劃-1143.最長公共子序列-力扣(LeetCode)_lintcode 最長公共子序列-CSDN博客
題目鏈接：1035. 不相交的線 - 力扣（LeetCode）
三、代碼示例
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size(),n = nums2.size();vector<vector<int>> dp(m+1,vector<int>(n+1,0));for(int i = 1;i<=m;i++){for(int j = 1;j<=n;j++){if(nums1[i-1] == nums2[j-1]){dp[i][j] = dp[i-1][j-1]+1;}else{dp[i][j] = max(dp[i-1][j],dp[i][j-1]);}}}return dp[m][n];}
};
?
?
看到最后，如果對您有所幫助，還請點贊、收藏和關注，點點關注不迷路，我們下期再見！?
)
)
)
)
