1.數據類型
2.如何選擇降維方法進行數據降維
3.線性降維：主成分分析（PCA）、線性判別分析（LDA）
4.非線性降維
5.基于特征選擇的降維
6.基于神經網絡的降維

??數據降維是將高維數據轉換為低維表示的過程，旨在保留關鍵信息的同時減少計算復雜度、去除噪聲或可視化數據。常見降維方法有幾類，分別對應不同數據采用。

方法類型	優點	缺點	適用場景
PCA	計算快、可解釋、保留全局結構	僅捕獲線性關系	特征相關性高、線性數據
t-SNE	可視化效果好、保留局部結構	計算慢、難以解釋、超參敏感	高維數據可視化（如單細胞RNA-seq）
UMAP	比t-SNE快、保留局部和部分全局結構	需調參	大規模非線性數據
LDA	最大化類別可分性	僅適用于分類、需標簽	有監督分類任務
自編碼器	處理復雜非線性關系	需要大量數據、訓練成本高	圖像、語音等高維非線性數據
特征選擇	保留原始特征、可解釋性強	可能丟失特征間交互信息	特征冗余明顯的結構化數據

一、數據類型

??雖然降維方法最初多用于數值型數據，但通過適當的預處理和轉換，非數值型數據（如類別型、文本、圖像、圖網絡等） 也可以使用降維技術。降維的核心是保留數據的本質結構，無論原始形式如何，文本是通過詞頻或語義嵌入捕捉語義相似性。圖數據是通過節點關系捕捉社區結構。類別數據是通過共現頻率或概率模型發現潛在模式。

1. 類別型數據（Categorical Data）

??（1）獨熱編碼（One-Hot Encoding）后降維：將類別變量轉為二進制向量（如性別“男/女”變為[1,0]和[0,1]），再使用PCA或t-SNE降維。獨熱編碼會大幅增加維度（“維度爆炸”），需配合降維。

2. 文本數據（Text Data）

??（1）詞袋模型（Bag-of-Words） + 降維：將文本轉為詞頻向量（TF-IDF）后，用PCA/NMF/LDA（潛在狄利克雷分配）降維。如新聞分類中，用NMF提取主題（每個主題是詞的加權組合）。
??（2）詞嵌入（Word Embedding）：直接使用預訓練的低維詞向量（如Word2Vec、GloVe）表示文本，或對句子/文檔向量化后降維。

3. 圖數據（Graph/Network Data）

??（1）圖嵌入（Graph Embedding）：將節點映射為低維向量（如Node2Vec、DeepWalk），保留圖的結構信息。
??（2）鄰接矩陣降維：對圖的鄰接矩陣或拉普拉斯矩陣進行PCA或SVD分解。

4. 圖像數據（Image Data）

??（1）傳統方法：對像素矩陣使用PCA（如人臉識別中的“特征臉”）。
??（2）深度學習方法：用卷積自編碼器（CAE）提取低維特征。

5. 混合型數據（數值+類別）

??（1）統一表征：對類別變量編碼（如目標編碼、嵌入），與數值變量拼接后降維。使用專門模型（如廣義低秩模型，GLRM）。

二、如何選擇降維方法進行數據降維

??降維方法需要綜合考慮數據特性、問題目標和方法假設。

1.判斷數據是否需要降維

（1）明確降維目標：

描述	方法推薦
可視化（降至2D/3D）	優先選非線性方法（t-SNE/UMAP）
減少計算開銷	線性方法（PCA）或特征選擇
去除噪聲/冗余特征	PCA、自動編碼器或特征選擇
提高模型性能	結合監督方法（LDA、嵌入法）

（2）檢查數據維度問題：

描述	方法推薦
特征數遠大于樣本數（如基因數據）	必須降維
特征間高度相關	PCA/線性方法有效
特征稀疏（如文本）	NMF或稀疏PCA

2.選擇降維方法的決策流程

（1）分析數據結構

數據特性	推薦方法
線性關系（特征間方差主導）	PCA、LDA（有標簽）、SVD
非線性流形（復雜拓撲）	t-SNE、UMAP、LLE、ISOMAP
混合類型數據	統一編碼后PCA，或廣義低秩模型（GLRM）
高稀疏性（如文本）	NMF、稀疏PCA

（2）是否帶標簽？
??有監督任務（分類/回歸），優先用LDA（線性）或監督自編碼器。特征選擇遞歸特征消除（RFE）、基于模型的重要性排序（如XGBoost）；無監督任務，PCA、t-SNE、UMAP等。

（3）是否需要可解釋性

特性	推薦方法
需要解釋特征貢獻	PCA（主成分可分析）、特征選擇。
無需解釋	自編碼器、t-SNE（側重可視化）。

（4）評估計算資源

特性	推薦方法
大規模數據	PCA、隨機投影、增量PCA（內存高效）。
小樣本高維數據	t-SNE、UMAP（但需調參）

三、線性降維

1.主成分分析（PCA）

??主成分分析（PCA，Principal Component Analysis）是一種統計方法，用于通過線性變換將數據降維，同時盡可能保留數據中的主要變異信息。它是一種無監督學習方法，廣泛應用于數據預處理、特征提取、降維、數據可視化和噪聲去除等領域。
（1）PCA的核心思想
??PCA的目標是將原始數據投影到一組新的坐標軸（主成分）上，使得這些坐標軸的方向能夠最大化數據的方差。 具體來說：
第一個主成分（PC1）：是數據中方差最大的方向。
第二個主成分（PC2）：是與PC1正交的方向中方差最大的方向。
后續主成分：依次類推，每個主成分都與之前的所有主成分正交，并且在剩余的方差中最大化。通過這種方式，PCA能夠將數據的主要結構保留下來，同時去除一些不重要的信息（如噪聲或冗余特征）。

（2）PCA的計算原理和過程代碼示例
在這個例子中：
第一個主成分解釋了50%的方差。
第二個主成分解釋了50%的方差。
兩個主成分的方差解釋率之和為100%，說明降維后的數據保留了原始數據的全部信息。

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import numpy as np# 示例數據
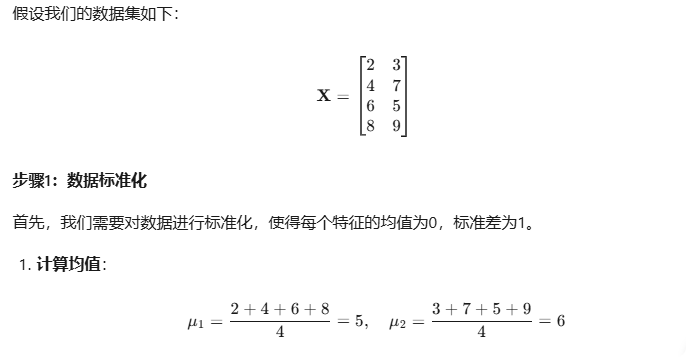
X = np.array([[2, 3],[4, 7],[6, 5],[8, 9]])# 數據標準化
scaler = StandardScaler()
X_scale = scaler.fit_transform(X)# 執行PCA
pca = PCA(n_components=2)  # 降維到2維
X_reduce = pca.fit_transform(X_scale)# 輸出結果
print("原始數據（標準化后）：\n", X_scale)
print("降維后的數據：\n", X_reduce)
print("主成分方向（特征向量）：\n", pca.components_)
print("方差解釋率：\n", pca.explained_variance_ratio_)

2.線性判別分析（LDA）

??線性判別分析（Linear Discriminant Analysis, LDA）是一種監督學習降維與分類方法，核心目標是通過線性變換將高維數據投影到低維空間，使得同類樣本盡可能緊湊、不同類樣本盡可能分離，從而提升分類性能。
（1）核心思想
??與無監督的 PCA 不同，LDA 利用類別標簽信息，通過最大化類間方差與最小化類內方差的比值，尋找最優投影方向。直觀理解，假設兩類數據在二維空間中分布，LDA 的目標是找到一條直線，使得兩類樣本在該直線上的投影滿足，類內樣本盡可能集中（類內方差小）；類間樣本中心距離盡可能遠（類間方差大）。

3.非負矩陣分解（NMF）

??將數據分解為非負矩陣的乘積，適用于所有特征為非負的場景（如圖像）。

4.奇異值分解（SVD）

??對矩陣進行分解，保留主要奇異值，常用于推薦系統和文本數據（如潛在語義分析）。

四、非線性降維

1.t-SNE（t-分布隨機鄰域嵌入）

??保留局部相似性，適合高維數據可視化（如將數據降至2D/3D），但計算開銷較大。

2.UMAP（均勻流形近似與投影）

??類似t-SNE，但計算效率更高，能同時保留局部和全局結構。

3.ISOMAP（等距映射）

4.局部線性嵌入（LLE）

五、基于特征選擇的降維

1.過濾法

??使用統計指標（如方差、卡方檢驗、互信息）選擇重要特征。

2.包裝法

??通過模型性能評估特征子集（如遞歸特征消除RFE）。

3.嵌入法

??模型訓練過程中自動選擇特征（如Lasso回歸、決策樹的特征重要性）。

六、基于神經網絡的降維

1.自編碼器（Autoencoder）

??通過編碼器壓縮數據，解碼器重建數據，隱層作為低維表示。可處理非線性關系。

2.變分自編碼器（VAE）

??在自編碼器中引入概率生成模型，適合生成任務。

3.深度非線性降維（如深度信念網絡）

??利用多層神經網絡學習復雜非線性映射。