算法	相關知識點	可以通過點擊	以下鏈接進行學習	一起加油！
雙指針	滑動窗口	二分查找	前綴和	位運算
模擬	鏈表	哈希表

在眾多字符串算法題中，有一類題目看起來沒有太多算法技巧，卻經常讓人“翻車”——那就是字符串模擬題。這類題型往往不依賴復雜的數據結構或高級算法，更多的是對邏輯構造能力、字符串操作細節以及邊界處理的考察。本文將通過幾個典型字符串模擬題的拆解，幫助你梳理解題思路、掌握通用技巧，從而在這類題目中穩住基本盤。

🌈個人主頁：是店小二呀
🌈C/C++專欄：C語言\ C++
🌈初/高階數據結構專欄： 初階數據結構\ 高階數據結構
🌈Linux專欄： Linux
🌈算法專欄：算法
🌈Mysql專欄:Mysql

🌈你可知:無人扶我青云志 我自踏雪至山巔

14. 最長公共前綴

【題目】：14. 最長公共前綴

【算法思路】

解法一：兩兩比較

通過兩兩比較的方式，不斷循環尋找字符不相等的位置，利用 substr 接口進行字符串剪切。這里，‘最長公共前綴’的意思是根據木桶效應，取最短字符串的長度作為‘最長公共前綴’的上限。

【代碼實現】

class Solution {
public:string longestCommonPrefix(vector<string>& strs) {//解法一：兩兩結合string tmp = strs[0];for(int i = 1; i< strs.size(); i++)tmp = findpRrefix(tmp, strs[i]);return tmp;}string findpRrefix(string& s1, string& s2){int i = 0;while(i < min(s1.size(), s2.size()) && s1[i] == s2[i]) i++;return s1.substr(0, i);}
};

解法二：統一比較

使用 char 類型變量記錄字符串中的元素，通過循環逐個比較字符是否相等。考慮到‘最長公共前綴’的上限，當某段完全相同的字符串長度等于當前遍歷的字符串長度時，說明已經達到了公共前綴的上限，此時可以直接返回結果。

【代碼實現】

class Solution {
public:string longestCommonPrefix(vector<string>& strs) {//解法二：統計比較for(int j = 0; j < strs[0].size(); j++){char ch = strs[0][j];for(int i = 0; i < strs.size(); i++){if( j == strs[i].size()  || strs[i][j] != ch) return strs[0].substr(0,j);}}return strs[0];}
};

---

5. 最長回文子串

【題目】：5. 最長回文子串

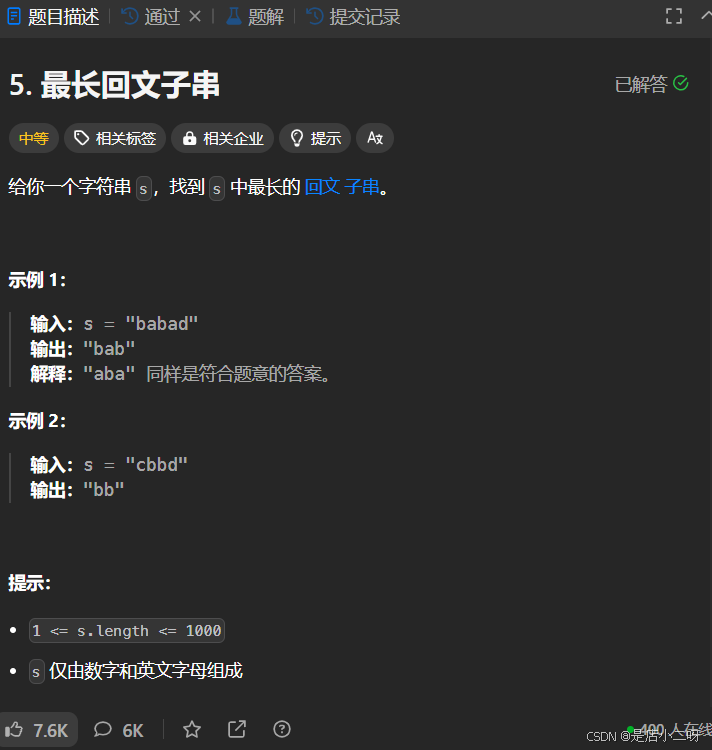
【算法思路】

解法：中心擴展算法

1. 固定一個中心點。
2. 從中心開始，向兩邊擴展。

注意：需要同時考慮奇數長度和偶數長度的回文情況。擴展過程中，若遇到越界或不符合回文性質時，停止并返回。中心擴展算法特別適用于回文數的對稱特性。

【代碼實現】

class Solution {
public:string longestPalindrome(string s) {//中心擴展算法int begin = 0, len = 0;int n = s.size();for(int i = 0; i < n; i++) //依次枚舉所有的中點{int left = i, rigth = i;//奇數擴張while(left >= 0 && rigth < n && s[left] == s[rigth]){left--;rigth++;}if(rigth - left - 1 > len){begin = left + 1;len = rigth - left - 1;}//偶數擴張left = i, rigth = i + 1;while(left >= 0 && rigth < n && s[left] == s[rigth]){left--;rigth++;}if(rigth - left - 1 > len){begin = left + 1;len = rigth - left - 1;}}return s.substr(begin,len);}
};

---

67. 二進制求和

【題目】：67. 二進制求和

【算法思路】

解法：高精度模擬加減乘除

高精度算法模擬了列豎式計算過程，通常稱為‘二進制高精度加法算法’，對于兩個字符串的處理從低位開始。需要特別注意進位處理邏輯，并且要處理前導零的情況。判斷條件為：當 cur >= 0 時，繼續處理到最前的數據，若不需要加上原數據，默認加0。

數字字符轉換為整型時：數字字符 - '0' 即得到整型值。

最后，使用 reverse 進行翻轉，以符合題目的要求。

【代碼實現】

class Solution {
public:string addBinary(string a, string b) {int cur1 = a.size() - 1, cur2 = b.size() - 1;int t = 0;string ret;while(cur1 >= 0 || cur2 >=0 || t ){if(cur1 >= 0)  t += a[cur1--] - '0'; if(cur2 >= 0)  t += b[cur2--] - '0'; ret += t % 2 + '0';t /= 2;}reverse(ret.begin(), ret.end());return ret;}
};

---

43. 字符串相乘

【題目】：43. 字符串相乘

【算法思路】

解法一："模擬"小學的列豎式運算

解法二：無進位相乘然后相加，最后處理進位

關于此類高精度題目，推薦先將原始字符串進行反轉，因為列豎式計算是從低位開始的。對于兩個字符串，先反轉它們，再將數字字符轉換為整型，通過數組存儲結果。我們創建的數組大小為 m + n - 1，其中 m 和 n 分別是兩個字符串的長度。通過數學或繪圖分析，可以發現這個剛好滿足累加所需的存儲空間。

這里使用無進位相乘然后相加，最后再處理進位。由于無論是先進行進位還是后進行進位，最終的結果是相同的，因此我們推薦先將結果存儲下來，然后再進行進位處理，這樣更為方便和簡潔，避免了細節很多存在的問題。

算法步驟：

第一步:將輸入的兩個字符串反轉，以便從低位開始進行處理。

第二步：對于兩個字符串中的數字，通過下標相加，其兩個數字結果正好對應數組中相應位置的值。在進行加法時，需使用 += 來累加結果。

第三步：在處理完所有操作后，可能會出現前導零的情況。最終需要使用 reverse 進行翻轉，并去掉多余的前導零。可以通過以下代碼來去除前導零：while (ret.size() > 1 && ret.back() == '0') ret.pop_back();

【代碼實現】

class Solution 
{
public:string multiply(string nums1, string nums2) {int n = nums1.size(), m = nums2.size();//字符串反轉reverse(nums1.begin(), nums1.end());reverse(nums2.begin(), nums2.end());vector<int> nums(m + n - 1);for(int i = 0; i < n; i++)for(int j = 0; j < m; j++)nums[i + j] += ((nums1[i] - '0') * (nums2[j] - '0')) ;//進位處理string ret;int t = 0, cur = 0;while( cur < m + n -1 || t){if(cur < m + n -1) t += nums[cur++];ret += t % 10 + '0';t /= 10;}//4.處理前導零while(ret.size() > 1 && ret.back() == '0') ret.pop_back();reverse(ret.begin(), ret.end());return ret;}
};

快和小二一起踏上精彩的算法之旅！關注我，我們將一起破解算法奧秘，探索更多實用且有趣的知識，開啟屬于你的編程冒險！