擴增子分析|R分析之微生物生態網絡穩定性評估之節點和連接的恒常性、節點持久性以及組成穩定性指數計算

?一、引言

?????? 周集中老師團隊于2021年在Nature climate change發表的文章，闡述了網絡穩定性評估的原理算法，并提供了完整的代碼。自此對微生物生態網絡的評估具有更全面的指標，自此網絡穩定性的評估廣受大家歡迎。本文將介紹網絡穩定性之節點和連接的恒常性、節點持久性以及組成穩定性的原理，計算方法以及代碼，如有疑問歡迎討論交流。

?????? 為了理解增溫是否以及如何影響構建的微生物生態網絡（MEN）的穩定性，我們使用了多種指標來表征網絡及其嵌入成員的穩定性，包括魯棒性、易損性、節點和連接的恒常性、節點持久性以及組成穩定性。我們通過消除模擬和經驗觀察評估了網絡及網絡內微生物群落的穩定性。上一節我們討論了基于模擬的方式評估網絡穩定性的穩健性（Robustness）和易損性指標。感興趣的可以跳轉至下述鏈接閱讀：

擴增子分析|微生物生態網絡穩定性評估之魯棒性（Robustness）和易損性（Vulnerability）

本節我們將討論基于實際觀測值評估網絡穩定性的節點和連接的恒常性、節點持久性以及組成穩定性指數。

二、基礎知識—基于實際觀測值的網絡穩定性分析

2.1 節點恒常性（Node constancy）

?????? 恒常性衡量物種的時間穩定性，定義為μ/σ，其中μ是隨時間變化的豐度平均值，σ是標準差。

?????? 式中，μi是平均值；

?????????????? σi是不同時間點網絡中物種i豐度的標準差。

?????? 僅當物種i在某一時間點處于 MEN 中時，物種i在某一時間點的豐度才為正。否則，物種i在該時間點的豐度被視為零。當σi= 0 時，恒常性不是有限的，因此將從后續分析中移除。最后，所有恒常性值的平均值被報告為不同條件下網絡節點的恒常性。使用 Mann-Whitney U檢驗?測試處理之間鏈接恒定性的差異。

?????? 然后，參考Hui等人提出的方法，計算多個網絡間的重疊節點數。被包含的時間點稱為“順序”。更高的重疊節點數量表示網絡中物種組成的周轉速度較慢。

2.2 連接恒常性（Link constancy）

類似于節點恒常性，計算連接恒常性。如果節點i和j在網絡中呈正相關，則令=?1；如果節點i和j在網絡中呈負相關，則令 = 1。如果i和j?之間沒有連接，則令=?= 0。連接恒常性（或）的計算方法如下：

??????????? 式中，

和分別為來自不同時間點所有網絡中的均值和標準差，和分別為來自不同時間點所有網絡中的均值和標準差。對于= 0或= 0的情況，從后續分析中刪除。最后，所有連接恒常性的平均值作為網絡連接的恒常性。

2.3 節點持久性（Node persistence）

?????? 節點持久性定義為生態系統中共存物種占物種總數的比例。因此，節點的持久性計算為連續多年存在于網絡中節點的百分比，計算方法是：

?????? 式中，v是在多個連續時間點采集的樣本數；

???????????????? S是網絡中的 OTU 總數；

是Dirac delta函數，如果樣本i中OTU k的?豐度大于 0，則= 1，如果樣本i中不存在OUT k ，則?= 0。

2.4 組成穩定性（Compositional stability）

????? 組成穩定性評估群落結構隨時間的變化。我們使用樣本×OTU矩陣計算了網絡中微生物群落的組成穩定性，如下所示

?????? 式中，v為在多個連續時間點從同區域采集的樣本數。S為網絡中的 OTU 總數。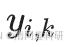為樣本i中 OUT k的豐度。若群落結構沒有變化，即，穩定性指數等于0。

當v= 2 時，

?????? 其中和分別是第i年和第i– 1 年樣本中OUT k的豐度?。

圖中，d,每兩年網絡化社區隨時間的變化組成穩定性。e ，組成穩定性和節點持久性的皮爾遜相關性。該線表示在變暖（紅色）或控制（藍色）條件下的最小二乘最佳擬合。f ，變暖組（紅色框）或控制組（藍色框）條件下網絡復雜性和穩定性指數之間的 Pearson 相關性。（網絡復雜性可根據相關代碼計算）這里顯示顯著（P ≤ 0.05 ?）相關性，橙色表示正相關，綠色表示負相關。單元格內的數字是相應的相關系數。P > 0.05 的相關性?標記為灰色。

三、示例數據和R代碼

本文的示例數據和代碼均來自于2021年周集中老師團隊的Nature climate change文章，感興趣的同學可以自行去學習。

3.1 組成穩定性指標

🌟準備數據

準備otu.csv表格，該表格為要計算魯棒性的網絡otu數據表。

代碼每次計算一個網絡的穩健性，因此需要計算幾個網絡就運行幾次代碼，每次將輸入文件名修改。

🌟完整代碼

# 加載自定義的 R 腳本，其中可能包含必要的自定義函數
source("ieggrtools.r")# 定義社區數據和處理數據的文件路徑
com.file = "input_file/OTUtable_NetworkedOTUs_AllSamples.txt"
treat.file = "input_file/SampleMap_AllSamples.txt"# 從文件中加載社區數據，并進行轉置
comm = t(lazyopen(com.file))
# 加載處理數據
treat = lazyopen(treat.file)# 檢查社區數據中是否有缺失值
sum(is.na(comm))
# 將所有的 NA 值替換為 0
comm[is.na(comm)] = 0# 匹配社區數據和處理數據的樣本名稱
sampc = match.name(rn.list = list(comm = comm, treat = treat))
comm = sampc$comm
treat = sampc$treat# 查看處理數據的前幾行，確認哪個列是 Plot_ID，哪個列是 Year
head(treat)# 獲取唯一的 Plot_ID 和按順序排列的 Year
plot.lev = unique(treat$Plot_ID)
year.lev = sort(unique(treat$Year))# 生成一個序列，用于計算多重順序穩定性（Zeta 多樣性水平）
zeta.lev = 2:length(year.lev)# 創建一個包含不同年份窗口的列表，用于計算 Zeta 多樣性
year.windows = lapply(1:length(zeta.lev), function(i) {zetai = zeta.lev[i]lapply(1:(length(year.lev) - zetai + 1), function(j) {year.lev[j:(j + zetai - 1)]})
})
names(year.windows) = zeta.lev
year.windows  # 顯示生成的年份窗口# 定義一個函數，用于計算一組樣本的社區穩定性
comstab <- function(subcom) {((nrow(subcom) * sum(apply(subcom, 2, min))) / sum(subcom))^0.5
}# 計算每個 Plot 在不同年份窗口內的穩定性
stabl = lapply(1:length(year.windows), function(i) {stabi = t(sapply(1:length(plot.lev), function(j) {plotj = plot.lev[j]sapply(1:length(year.windows[[i]]), function(k) {yearwdk = year.windows[[i]][[k]]# 找到滿足條件的樣本sampijk = rownames(treat)[which((treat$Plot_ID == plotj) & (treat$Year %in% yearwdk))]outijk = NA# 檢查樣本數量是否匹配年份窗口if (length(sampijk) < length(yearwdk)) {warning("plot ", plotj, " has missing year in year window ", paste(yearwdk, collapse = ","))} else if (length(sampijk) > length(yearwdk)) {warning("plot ", plotj, " has duplicate samples in at least one year of window ", paste(yearwdk, collapse = ","))} else {# 計算樣本的社區穩定性comijk = comm[which(rownames(comm) %in% sampijk), , drop = FALSE]outijk = comstab(comijk)}outijk})}))# 確保行數和 Plot_ID 的數量匹配if (nrow(stabi) != length(plot.lev) & nrow(stabi) == 1) {stabi = t(stabi)}rownames(stabi) = plot.levcolnames(stabi) = sapply(year.windows[[i]], function(v) {paste0("Zeta", zeta.lev[i], paste0(v, collapse = ""))})stabi
})
# 將所有的穩定性數據合并成一個矩陣
stabm = Reduce(cbind, stabl)# 移除特定年份 (Y09) 并注釋每個 Plot 的處理信息
treat.rm09 = treat[which(treat$Year != "Y09"), , drop = FALSE]
output = data.frame(treat.rm09[match(rownames(stabm), treat.rm09$Plot_ID), 1:5, drop = FALSE], stabm, stringsAsFactors = FALSE)
output = output[order(output$Warming, output$Clipping, output$Precip, output$Plot_ID), , drop = FALSE]
head(output)  # 顯示輸出的前幾行# 加載 tidyr 包，用于數據轉換
library(tidyr)# 將穩定性數據轉換為長格式，方便繪圖
cs.mo = output
cs.long = gather(cs.mo, year, cs, Zeta2Y09Y10:Zeta6Y09Y10Y11Y12Y13Y14, factor_key = TRUE)
cs.long = cs.long[-which(is.na(cs.long$cs)), ]
cs.long$EndYear = as.numeric(gsub(".*Y", "", cs.long$year))# 定義一個函數，用于生成線性模型文本
get_text <- function(y, x) {lm = lm(y ~ x)lm_p = round(summary(lm)$coefficients[2, 4], 3)lm_r = round(summary(lm)$adj.r.squared, 3)lm_s = round(summary(lm)$coefficients[2, 1], 3)txt = paste(lm_s, " (", lm_r, ", ", lm_p, ")", sep = "")return(txt)
}# 定義一個函數，用于繪制完整的社區穩定性圖
plot_cs_full <- function(xc, yc, xw, yw) {plot(yw ~ xw, ylim = c(0.2, 1), xlim = c(10, 14), ylab = "Compositional stability", xlab = "Year", pch = 19, cex.axis = 0.7, cex.lab = 0.7, tck = -0.03, col = "#e7211f")abline(lm(yw ~ xw), col = "#e7211f")points(yc ~ xc, col = "#214da0")abline(lm(yc ~ xc), col = "#214da0")txt1 = get_text(yw, xw)txt2 = get_text(yc, xc)mtext(txt1, side = 3, line = 0.8, cex = 0.5, col = "#e7211f")mtext(txt2, side = 3, line = 0.1, cex = 0.5, col = "#214da0")
}# 定義一個函數，用于繪制 Zeta6 穩定性圖，并進行 Wilcoxon 檢驗
plot_cs_zeta6 <- function(xc, yc, xw, yw) {plot(yw ~ xw, ylim = c(0.2, 1), xlim = c(10, 14), ylab = "Compositional stability", xlab = "Year", pch = 19, cex.axis = 0.7, cex.lab = 0.7, tck = -0.03, col = "#e7211f")points(yc ~ xc, col = "#214da0")wt = wilcox.test(yw, yc)mtext(paste(wt$statistic, wt$p.value, sep = ","), cex = 0.5)
}# 繪制 Figure 3d：相鄰兩年的組分穩定性
# 設置顏色和符號
colors = c(rep("#214da0", 5), rep("#e7211f", 5))
syms = c(1, 1, 1, 1, 1, 19, 19, 19, 19, 19)
# 定義一個函數 plot_cs，用于繪制穩定性圖，帶誤差條
plot_cs <- function(yw, yc, ebw, ebc) {x = c(1, 2, 3, 4, 5)yl = c(min(c(yw - ebw, yc - ebc)), max(c(yw + ebw, yc + ebc)))# 繪制加溫處理 (W) 的數據及回歸線plot(yw ~ x, ylim = yl, ylab = "Compositional stability", xlab = "Year of warming", pch = 19, cex.axis = 0.7, cex.lab = 0.7, tck = -0.03, col = "red")abline(lm(yw ~ x), col = "red")arrows(x, yw - ebw, x, yw + ebw, length = 0.05, angle = 90, code = 3, col = "red")# 繪制無加溫處理 (N) 的數據及回歸線points(yc ~ x, col = "blue")abline(lm(yc ~ x), lty = 2, col = "blue")arrows(x, yc - ebc, x, yc + ebc, length = 0.05, angle = 90, code = 3, col = "blue")# 獲取線性模型文本txt1 = get_text(yw, x)txt2 = get_text(yc, x)# 添加文本到圖表中mtext(txt1, side = 3, line = 0.8, cex = 0.5, col = "red")mtext(txt2, side = 3, line = 0.1, cex = 0.5, col = "blue")
}# 篩選 Zeta2 數據并計算均值和標準差
zeta2 = cs.long[grep("Zeta2", cs.long$year), ]
zeta2_means = aggregate(zeta2$cs, list(zeta2$Warming, zeta2$EndYear), FUN = mean)
zeta2_sds = aggregate(zeta2$cs, list(zeta2$Warming, zeta2$EndYear), FUN = sd)# 繪制相鄰年份的組分穩定性圖
plot_cs(yw = zeta2_means$x[which(zeta2_means$Group.1 == "W")],yc = zeta2_means$x[which(zeta2_means$Group.1 == "N")],ebw = zeta2_sds$x[which(zeta2_sds$Group.1 == "W")],ebc = zeta2_sds$x[which(zeta2_sds$Group.1 == "N")])#################即可完成組合穩定性隨時間變化圖#####################

🌟輸出結果

????? 圖片解讀，紅色是變溫，藍色是對照。數字0.071是線性擬合斜率，0.862和0.015是調整后的r2和P值。

3.2 節點恒常性指標

🌟準備數據

準備OTUtable_NetworkedOTUs_AllSamples.csv表格，該表格為要節點恒常性的otu數據表

準備SampleMap_AllSamples.csv表格，樣本基本映射文件

🌟完整代碼

# 清理工作環境中的所有對象
rm(list = ls())# 加載所需的 R 包
library(ggplot2)  # 用于數據可視化
library(gridExtra)  # 用于排列多個圖表# 讀取 OTU 表和樣本映射文件
otu <- read.csv("OTUtable_NetworkedOTUs_AllSamples.csv",  header=T, row.names=1)
map <- read.csv("SampleMap_AllSamples.csv",  header=T)# 定義每年樣本的索引
id_09 = rep(which(map$Year == "Y09"), each=2)  # 重復每個索引兩次
id_10 = which(map$Year == "Y10")
id_11 = which(map$Year == "Y11")
id_12 = which(map$Year == "Y12")
id_13 = which(map$Year == "Y13")
id_14 = which(map$Year == "Y14")# 檢查樣本的 plot 順序
data.frame(map$Plot_full_name[id_09],map$Plot_full_name[id_10],map$Plot_full_name[id_11],map$Plot_full_name[id_12],map$Plot_full_name[id_13],map$Plot_full_name[id_14])# 獲取第 14 年的溫度處理（是否加溫）
warming_trt = map$Warming[id_14]# 將 OTU 表按年份拆分為不同數據框
otu_09 = as.data.frame(otu[, id_09])
otu_10 = as.data.frame(otu[, id_10])
otu_11 = as.data.frame(otu[, id_11])
otu_12 = as.data.frame(otu[, id_12])
otu_13 = as.data.frame(otu[, id_13])
otu_14 = as.data.frame(otu[, id_14])# 檢查 OTU 表的樣本順序是否與映射文件一致
sum(names(otu_09) != map$Sample[id_09])  # 檢查列名是否與樣本名稱匹配
sum(names(otu_10) != map$Sample[id_10])
sum(names(otu_11) != map$Sample[id_11])
sum(names(otu_12) != map$Sample[id_12])
sum(names(otu_13) != map$Sample[id_13])
sum(names(otu_14) != map$Sample[id_14])# 計算節點穩定性（constancy）
# 計算每個 OTU 的平均值
otu_mean = (otu_09 + otu_10 + otu_11 + otu_12 + otu_13 + otu_14) / 6
# 計算標準差
otu_sd = sqrt(((otu_09 - otu_mean)^2 + (otu_10 - otu_mean)^2 + (otu_11 - otu_mean)^2 +(otu_12 - otu_mean)^2 + (otu_13 - otu_mean)^2 + (otu_14 - otu_mean)^2) / 5)
# 計算節點穩定性為平均值除以標準差
otu_constancy = otu_mean / otu_sd# 將節點穩定性結果保存為 CSV 文件
write.table(otu_constancy, "observed_constancy_of_each_node.csv", sep=",")# 根據溫度處理分割節點穩定性數據
otu_constancy_w = otu_constancy[, which(warming_trt == "W")]  # 加溫處理
otu_constancy_c = otu_constancy[, which(warming_trt == "N")]  # 控制處理# 計算每個 OTU 在加溫和控制處理下的平均節點穩定性
otu_constancy_w_avg = rowMeans(otu_constancy_w)
otu_constancy_c_avg = rowMeans(otu_constancy_c)# 提取有限值的節點穩定性
con_w = otu_constancy_w_avg[is.finite(otu_constancy_w_avg)]
con_c = otu_constancy_c_avg[is.finite(otu_constancy_c_avg)]# 創建一個數據框，用于繪圖
nc_df = data.frame(warming = c(rep("control", length(con_c)), rep("warming", length(con_w))),nc = c(con_c, con_w))# 使用 ggplot2 繪制箱線圖和散點圖
ggplot(nc_df, aes(x = warming, y = nc, fill = warming)) +geom_boxplot(alpha = 1, width = 0.4, outlier.shape = NA) +  # 繪制箱線圖，不顯示離群點geom_jitter(shape = 16, size = 0.5, position = position_jitterdodge(jitter.width = 0.01, dodge.width = 0.8)) +  # 繪制抖動的散點圖scale_fill_manual(values = c("#214da0", "#e7211f")) +  # 設置填充顏色labs(y = "Node constancy") +  # 設置 y 軸標簽theme(axis.line = element_line(colour = "black"),  # 軸線顏色為黑色panel.grid.major = element_blank(),  # 移除主要網格線panel.grid.minor = element_blank(),  # 移除次要網格線panel.background = element_blank(),  # 移除背景panel.border = element_rect(colour = "black", fill = NA, size = 0.6),  # 設置邊框legend.position = "none"  # 不顯示圖例)

🌟輸出結果

3.3 連接恒常性指標

🌟準備數據

準備NetworkEdgeTable_AllNetworks.csv表格，即邊屬性表，該表可由網絡構建上游分析獲得。

🌟完整代碼

# 清理工作環境中的所有對象
rm(list = ls())
# 讀取網絡連接表
edge_prop = read.csv("NetworkEdgeTable_AllNetworks.csv", header=T)
edge_prop$edge_sign = paste(edge_prop$edge, edge_prop$V5, sep="_")  # 創建帶符號的邊緣標識
# 計算唯一連接的總數和帶符號的總數
total_e = length(unique(edge_prop$edge))
total_e_sign = length(unique(edge_prop$edge_sign))  # 注意：符號是一致的
# 創建連接表
edge_table = data.frame(matrix(NA, nrow=total_e, ncol=11))
row.names(edge_table) = unique(edge_prop$edge)
names(edge_table) = unique(edge_prop$year_trt)
# 填充連接表
for (i in 1:ncol(edge_table)) {edge_prop_year = edge_prop[which(edge_prop$year_trt == names(edge_table[i])), ]edge_table[which(rownames(edge_table) %in% edge_prop_year$edge), i] = 1
}
edge_table[is.na(edge_table)] <- 0  # 將 NA 替換為 0# 查看連接表的前幾行
head(edge_table)# 計算平均值和標準差
edge_table$avg_c = rowMeans(edge_table[, c(1, 2, 4, 6, 8, 10)])
edge_table$sd_c = apply(edge_table[, c(1, 2, 4, 6, 8, 10)], 1, FUN=sd)
edge_table$avg_w = rowMeans(edge_table[, c(1, 3, 5, 7, 9, 11)])
edge_table$sd_w = apply(edge_table[, c(1, 3, 5, 7, 9, 11)], 1, FUN=sd)# 計算恒常性
edge_table$constancy_c = edge_table$avg_c / edge_table$sd_c
edge_table$constancy_w = edge_table$avg_w / edge_table$sd_w# 處理無窮大值
edge_table$constancy_c[is.infinite(edge_table$constancy_c)] = NA
edge_table$constancy_w[is.infinite(edge_table$constancy_w)] = NA# edge_table[1:100,]# 計算鏈接恒常性的相關統計
v_constancy_c = edge_table$constancy_c[which(!is.na(edge_table$constancy_c))]
n_constancy_c = sum(!is.na(edge_table$constancy_c))
avg_constancy_c = mean(edge_table$constancy_c, na.rm=T)
sd_constancy_c = sd(edge_table$constancy_c, na.rm=T)v_constancy_w = edge_table$constancy_w[which(!is.na(edge_table$constancy_w))]
n_constancy_w = sum(!is.na(edge_table$constancy_w))
avg_constancy_w = mean(edge_table$constancy_w, na.rm=T)
sd_constancy_w = sd(edge_table$constancy_w, na.rm=T)# 進行 t 檢驗
t.test(v_constancy_w, v_constancy_c)library(ggplot2)# 繪制擴展數據圖 5d - 連接恒常性
df_lc_uw = data.frame(Treatment = c("control", "warming"), Link_constancy = c(avg_constancy_c, avg_constancy_w), se = c(sd_constancy_c / sqrt(n_constancy_c), sd_constancy_w / sqrt(n_constancy_w))
)# 創建條形圖
ggplot(df_lc_uw, aes(x=Treatment, y= Link_constancy)) +geom_bar(stat="identity", fill=c("#214da0", "#e7211f"), width=0.5) +geom_errorbar(aes(ymin=Link_constancy - se, ymax=Link_constancy + se), width=0.2) +labs(x="Treatment", y="Unweighted link constancy") +  # 添加中文標簽theme(axis.line = element_line(colour="black"),panel.grid.major = element_blank(),panel.grid.minor = element_blank(),panel.background = element_blank(),panel.border = element_rect(colour="black", fill=NA, size=0.6),legend.position="none")  # 隱藏圖例

🌟輸出結果

3.4 節點持久性指標

🌟準備數據

準備OTUtable_NetworkedOTUs_AllSamples.csv表格，該表格為要節點恒常性的otu數據表。

準備SampleMap_AllSamples.csv表格，樣本基本映射文件

🌟完整代碼

# 清理工作環境中的所有對象
rm(list = ls())# 讀取 OTU 表和樣本映射文件
otutab <- read.csv("OTUtable_NetworkedOTUs_AllSamples.csv",  header=T, row.names=1)
treatused <- read.csv("SampleMap_AllSamples.csv",  header=T)### 計算每個樣地的持久性
## 這里持久性 = 在特定年份中物種的比例
comm <- t(otutab)  # 轉置OTU表
sum(row.names(comm) == row.names(treatused))  # 確保樣本名稱匹配fake09.N <- comm[1:24, ]
row.names(fake09.N) <- gsub("S", "N", row.names(fake09.N))  # 替換樣本名稱
comm2 <- rbind(fake09.N, comm)  # 合并數據fake09.treat <- treatused[1:24, ]
row.names(fake09.treat) <- gsub("S", "N", row.names(fake09.treat))  # 替換樣本名稱
fake09.treat$Plot_full_name <- gsub("S", "N", fake09.treat$Plot_full_name)  # 替換樣地名稱
fake09.treat$Plot_ID <- gsub("S", "N", fake09.treat$Plot_ID)
treat2 <- rbind(fake09.treat, treatused)  # 合并處理數據
treat2$Plot_ID = factor(treat2$Plot_ID)  # 轉換為因子# 組織09年的升溫處理
treat2$Warming[1:48] <- treat2$Warming[49:96][match(treat2$Plot_ID[1:48], treat2$Plot_ID[49:96])]# 按照樣地ID分割數據
test1 <- split(data.frame(comm2), treat2$Plot_ID)# 定義年份
years = c("Y09", "Y10", "Y11", "Y12", "Y13", "Y14")
l <- rep(list(0:1), 6)
allcombines <- expand.grid(l)  # 生成所有組合
allcombines <- allcombines[c(4, 7, 13, 25, 49, 8, 15, 29, 57, 16, 31, 61, 32, 63, 64), ]  # 僅選擇相鄰年份
allcombines <- t(allcombines)# 計算持久性
test <- sapply(test1, function(x) {test3 <- sapply(1:ncol(allcombines), function(i) {coms <- allcombines[, i] * xtotal.sp <- sum(colSums(coms > 0) > 0)  # 計算總物種數persist.sp <- sum(colSums(coms > 0) == sum(allcombines[, i]))  # 計算持久物種數prop = persist.sp / total.sp  # 計算比例names(prop) = paste0(years[allcombines[, i] > 0], collapse = "")prop})test3
})# 整理結果
persist.result <- t(test)
output = data.frame(treat2[match(rownames(persist.result), treat2$Plot_ID), 1:5, drop=FALSE], persist.result, stringsAsFactors = FALSE)
names(output) <- paste(c(rep("", 5),rep("Zeta2", 5),rep("Zeta3", 4),rep("Zeta4", 3),rep("Zeta5", 2),rep("Zeta6", 1)), names(output), sep="")
head(output)
#輸出結果文件
write.csv(output, "MultiOrderPersistence.csv")library(tidyr)
## 繪制圖 S7fghij - 多級持久性
op.mo = outputop.long <- gather(op.mo, year, op, Zeta2Y09Y10:Zeta6Y09Y10Y11Y12Y13Y14, factor_key=TRUE)  # 轉換為長格式
op.long$EndYear = as.numeric(gsub(".*Y", "", op.long$year))  # 提取結束年份# 定義文本提取函數
get_text <- function(y, x) {lm = lm(y ~ x) lm_p = round(summary(lm)$coefficients[2, 4], 3)lm_r = round(summary(lm)$adj.r.squared, 3)lm_s = round(summary(lm)$coefficients[2, 1], 3)	txt = paste(lm_s, " (", lm_r, ", ", lm_p, ")", sep="")	return(txt)
}# 繪制持久性圖
plot_op_full <- function(xc, yc, xw, yw) {plot(yw ~ xw, ylim=c(0, 0.3), xlim=c(10, 14), ylab="Node persistence", xlab="Year", pch=19, cex.axis=0.7, cex.lab=0.7, tck=-0.03, col="#e7211f")abline(lm(yw ~ xw), col="#e7211f")  # 添加回歸線points(yc ~ xc, col="#214da0")  # 繪制控制組abline(lm(yc ~ xc), col="#214da0")  # 添加回歸線txt1 = get_text(yw, xw)txt2 = get_text(yc, xc)mtext(txt1, side=3, line=0.8, cex=0.5, col="#e7211f")  # 顯示文本mtext(txt2, side=3, line=0.1, cex=0.5, col="#214da0")
}# 繪制每個Zeta的圖
par(mfrow=c(2, 3))
plot_op_full(xc=op.long$EndYear[intersect(which(op.long$Warming=="N"), grep("Zeta2", op.long$year))], yc=op.long$op[intersect(which(op.long$Warming=="N"), grep("Zeta2", op.long$year))], xw=op.long$EndYear[intersect(which(op.long$Warming=="W"), grep("Zeta2", op.long$year))], yw=op.long$op[intersect(which(op.long$Warming=="W"), grep("Zeta2", op.long$year))])plot_op_full(xc=op.long$EndYear[intersect(which(op.long$Warming=="N"), grep("Zeta3", op.long$year))], yc=op.long$op[intersect(which(op.long$Warming=="N"), grep("Zeta3", op.long$year))], xw=op.long$EndYear[intersect(which(op.long$Warming=="W"), grep("Zeta3", op.long$year))], yw=op.long$op[intersect(which(op.long$Warming=="W"), grep("Zeta3", op.long$year))])plot_op_full(xc=op.long$EndYear[intersect(which(op.long$Warming=="N"), grep("Zeta4", op.long$year))], yc=op.long$op[intersect(which(op.long$Warming=="N"), grep("Zeta4", op.long$year))], xw=op.long$EndYear[intersect(which(op.long$Warming=="W"), grep("Zeta4", op.long$year))], yw=op.long$op[intersect(which(op.long$Warming=="W"), grep("Zeta4", op.long$year))])plot_op_full(xc=op.long$EndYear[intersect(which(op.long$Warming=="N"), grep("Zeta5", op.long$year))], yc=op.long$op[intersect(which(op.long$Warming=="N"), grep("Zeta5", op.long$year))], xw=op.long$EndYear[intersect(which(op.long$Warming=="W"), grep("Zeta5", op.long$year))], yw=op.long$op[intersect(which(op.long$Warming=="W"), grep("Zeta5", op.long$year))])plot_op_zeta6(xc=op.long$EndYear[intersect(which(op.long$Warming=="N"), grep("Zeta6", op.long$year))], yc=op.long$op[intersect(which(op.long$Warming=="N"), grep("Zeta6", op.long$year))], xw=op.long$EndYear[intersect(which(op.long$Warming=="W"), grep("Zeta6", op.long$year))], yw=op.long$op[intersect(which(op.long$Warming=="W"), grep("Zeta6", op.long$year))])# 繪制相鄰兩年的觀察到的持久性
colors = c(rep("#214da0", 5), rep("#e7211f", 5))
syms = c(1, 1, 1, 1, 1, 19, 19, 19, 19, 19)plot_op <- function(yw, yc, ebw, ebc) {x = c(1, 2, 3, 4, 5)yl = c(min(c(yw - ebw, yc - ebc)), max(c(yw + ebw, yc + ebc)))plot(yw ~ x, ylim=yl, ylab="Observed Node Persistence", xlab="Year of warming", pch=19, cex.axis=0.7, cex.lab=0.7, tck=-0.03, col="red")abline(lm(yw ~ x), col="red")  # 添加回歸線arrows(x, yw - ebw, x, yw + ebw, length=0.05, angle=90, code=3, col="red")  # 添加誤差條points(yc ~ x, col="blue")  # 繪制控制組abline(lm(yc ~ x), lty=2, col="blue")  # 添加回歸線arrows(x, yc - ebc, x, yc + ebc, length=0.05, angle=90, code=3, col="blue")  # 添加誤差條txt1 = get_text(yw, x)txt2 = get_text(yc, x)mtext(txt1, side=3, line=0.8, cex=0.5, col="red")  # 顯示文本mtext(txt2, side=3, line=0.1, cex=0.5, col="blue")
}# 提取Zeta2的數據
zeta2 = op.long[grep("Zeta2", op.long$year), ]
zeta2_means = aggregate(zeta2$op, list(zeta2$Warming, zeta2$EndYear), FUN=mean)  # 計算均值
zeta2_sds = aggregate(zeta2$op, list(zeta2$Warming, zeta2$EndYear), FUN=sd)  # 計算標準差# 繪制Zeta2的觀察到的持久性
plot_op(yw=zeta2_means$x[which(zeta2_means$Group.1 == "W")], yc=zeta2_means$x[which(zeta2_means$Group.1 == "N")], ebw=zeta2_sds$x[which(zeta2_sds$Group.1 == "W")], ebc=zeta2_sds$x[which(zeta2_sds$Group.1 == "N")])

🌟輸出結果

??????? 圖片解讀，紅色是變溫，藍色是對照。數字0.048是線性擬合斜率，0.866和0.014是調整后的r2和P值。