📘考研數據結構基礎：二叉樹的存儲、遍歷與隊列輔助實現詳

在數據結構的學習中，二叉樹作為一種結構清晰、應用廣泛的樹形結構，是考研計算機專業課中重點內容之一。本文將以實際代碼為基礎，介紹二叉樹的存儲結構、遍歷方式，以及在遍歷過程中為何要使用隊列結構，并解答一個常見疑問：“為什么不能用 char 類型直接代替隊列的元素類型”。

🧩一、二叉樹的存儲方式：鏈式存儲結構

在實際開發或算法設計中，二叉樹常采用鏈式存儲結構。其基本定義如下：

typedef struct BiTNode {char data;struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;

• 每個結點由一個字符 data 表示數據域。
• lchild 和 rchild 分別指向該結點的左、右子樹。
• BiTree 是指向 BiTNode 的指針，代表一個樹的根結點。

🧪二、二叉樹的遍歷方式

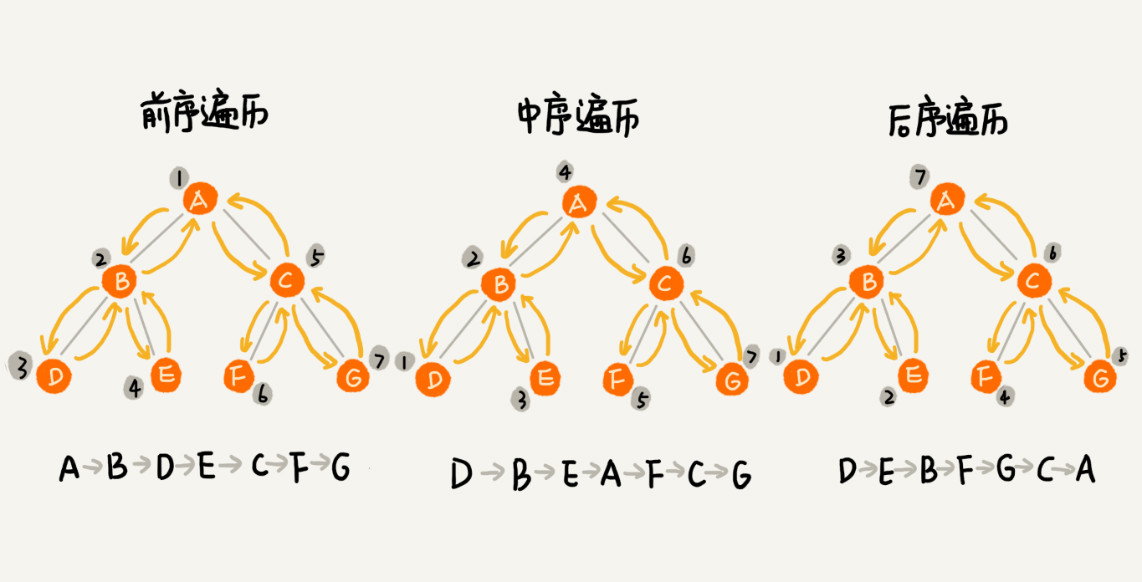
? 1. 先序遍歷（PreOrder）

void PreOrder(BiTree T) {if (T) {cout << T->data;PreOrder(T->lchild);PreOrder(T->rchild);}
}

先訪問根結點，再遞歸遍歷左子樹和右子樹。

---

? 2. 中序遍歷（InOrder）

void InOrder(BiTree T) {if (T) {InOrder(T->lchild);cout << T->data;InOrder(T->rchild);}
}

先訪問左子樹，再訪問根結點，最后遍歷右子樹。

---

? 3. 后序遍歷（PostOrder）

void PostOrder(BiTree T) {if (T) {PostOrder(T->lchild);PostOrder(T->rchild);cout << T->data;}
}

先遍歷左右子樹，最后訪問根結點。

---

? 4. 層序遍歷（LevelOrder）

層序遍歷不同于上面三種遞歸遍歷，它需要用輔助隊列實現。

void LevelOrder(BiTree T) {LinkQueue Q;InitQ(Q);EntQ(Q, T);while (!EmptyQ(Q)) {BiTree p;DelQ(Q, p);cout << p->data;if (p->lchild)EntQ(Q, p->lchild);if (p->rchild)EntQ(Q, p->rchild);}
}

---

🚩三、輔助隊列結構及其核心設計

為了支持層序遍歷的廣度優先訪問，我們需要一個隊列，隊列中存放的是樹結點的指針而非字符：

typedef BiTree ElemType;  // 關鍵設計：定義隊列的元素類型為 BiTree（即指向樹結點的指針）

隊列的基本操作如下：

bool EntQ(LinkQueue &Q, ElemType x);    // 入隊
bool DelQ(LinkQueue &Q, ElemType &x);   // 出隊

?為什么不能直接將 ElemType 改為 char？

這是許多初學者常見的疑惑。解釋如下：

• char 僅能存儲字符，比如 'A'，卻無法提供關于該字符結點的結構信息。

• 層序遍歷時，我們需要訪問一個結點的左右孩子：

  if (p->lchild) EntQ(Q, p->lchild);
  

  這里 p 是一個指向結構體的指針，如果你僅保存了 char，根本無法訪問 p->lchild。

? 所以，隊列中必須保存的是 BiTree 類型的指針，從而能繼續遞歸或迭代處理其子樹。

---

🧵四、二叉樹的構建

構建過程通常采用先序遞歸建樹法，使用 '#' 表示空結點：

void CreateTree(BiTree &T) {char ch;cin >> ch;if (ch == '#')T = NULL;else {T = new BiTNode;T->data = ch;CreateTree(T->lchild);CreateTree(T->rchild);}
}

輸入示例（先序）：

AB#D##C##

表示結構如下的樹：

    A/ \B   C\D

---

🔚五、總結與考研建議

知識點	內容
存儲結構	常用鏈式存儲，結構清晰，動態性強
遍歷方法	先序、中序、后序、層序，掌握遞歸與非遞歸實現
輔助結構	層序遍歷需要隊列，存儲的是結點指針 BiTree
設計技巧	使用 typedef ElemType 抽象數據類型，增強復用性

---

完整代碼《僅供參考》

function.h

 //層次建樹   借助一個輔助隊列//          a//        b   c//    d   e   f   g

    #ifndef LEVELIRDER3_FUNCTION_H#define LEVELIRDER3_FUNCTION_H#include <stdio.h>#include <stdlib.h>#include <ostream>using namespace std;//樹的結構體定義typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;}BiTNode , * BiTree;//隊列的結構體的聲明typedef BiTree ElemType;typedef struct LinkNode{ElemType datac;//在進行入隊的時候 這里使用的是 int 類型的的數據 然而樹存儲的是一個char  類型的這時候就體現出的了 typedef 的作用了 不用頻繁的修改數據struct LinkNode * next;}LinkNode;typedef struct {  //聲明一個結構體類型的指針LinkNode * front, * rear;}LinkQueue;void InitQ(LinkQueue &Q);bool EmptyQ(LinkQueue Q);//這里出入隊列 實際上是對 樹 的結點進行 的一個操作 所以應該使用 樹的 結構體類型bool EntQ(LinkQueue &Q,ElemType x);bool DelQ(LinkQueue &Q, ElemType &x);// 建立一個輔助隊列 tag  進行層序建樹typedef struct tag{//    BiTree p;  //樹的某一結點的地址值BiTNode *p;struct tag *pnext;}tag_t , *ptag_t;#endif //LEVELIRDER3_FUNCTION_H

queue.cpp

   //// Created by Yhame on 2025/5/11.//#include "function.h"//初始化void InitQ(LinkQueue &Q){//這里的結構體類型  LinkNodeQ.front = Q.rear =(LinkNode*) malloc(sizeof(LinkNode));Q.front->next =NULL; //隊頭指向NULL}//判空 這里可以不用判斷隊列是否會滿bool EmptyQ(LinkQueue Q){if(Q.front == Q.rear)return true;//    Q.front->next =NULL;//    return true;}//入隊bool EntQ(LinkQueue &Q,ElemType x){//插入LinkNode *s =(LinkNode*)malloc(sizeof(LinkNode)); //申請新的結點 插入隊尾if(!s)return false;s->datac =x;   //尾巴插入Q.rear->next =s;   //尾部入隊  尾指針的指向ss->next =NULL;  //s的指向NULLQ.rear =s;  //更新尾指針return true;}//出隊bool DelQ(LinkQueue &Q,ElemType &x){ //判空 從頭開始刪除if(Q.front ==Q.rear){return false;}LinkNode *q ;x = Q.front->next->datac; //返回要刪除的數據q = Q.front->next;  //q指向第一個數據結點  隊頭出Q.front->next =q ->next;  //斷開q 使front 指向后一個元素if(Q.rear==q){Q.rear = Q.front; // rear也回到front（空隊列狀態）}free(q);//如果q 為最后一個結點  使front 和rear 相等return true;}

main.cpp

     #include <iostream>#include "function.h"//前序遍歷void PreOrder(BiTree p){if(p!=NULL){printf("%c",p->data);PreOrder(p->lchild);PreOrder(p->rchild);}}//中序遍歷void InOrder(BiTree p){if(p!=NULL){InOrder(p->lchild);printf("%c",p->data);InOrder(p->rchild);}}//后序遍歷void PostOrder(BiTree p){if(p!=NULL){PostOrder(p->lchild);PostOrder(p->rchild);printf("%c",p->data);}}//層次遍歷void LevelOrder(BiTree T){LinkQueue Q; //聲明一個 輔助隊列InitQ(Q);BiTree p;  //記錄樹的當前結點//    BiTNode * p;EmptyQ(Q);EntQ(Q,T);  //樹根入隊當隊列不為空進行 隊頭出隊打印   之后判斷 該點的 左右孩子是否為空  進行出入隊操作puts("層序");while(!EmptyQ(Q)){DelQ(Q,p); //出隊當前結點 并打印putchar(p->data);  //printf("%c,c);if(p->lchild!=NULL){EntQ(Q,p->lchild);}if(p->rchild!=NULL){EntQ(Q,p->rchild);}}}int main() {BiTree pnew; //用來指向新申請的數結點BiTree tree =NULL; //tree 是指向樹根的，代表樹ptag_t phead= NULL,ptail =NULL, listpnew =NULL, pre =NULL; //初始化隊列 定義一個pre 指向執行的當前元素char c;這里使用的是 tag 的方法去建立一棵樹，通過輔助隊列來實現的 層序遍歷//abcdefwhile(scanf("%c",&c)){if(c=='\n'){break;}//calloc申請空間  大小是兩個參數相乘，并對空間進行初始化  賦值為0;//malloc 申請以后還需要對其進行賦值 malloc 返回的是 void * 類型的 也需要進行強制轉換樹申請結點pnew =(BiTree) calloc(1,sizeof(BiTNode));pnew->data = c;//隊列結點申請空間listpnew = (ptag_t) calloc(1,sizeof(tag_t));  //申請一個結構體類型的結點 返回一個指針類型的listpnew->p =pnew;//如果是數的第一個結點if(tree==NULL){tree = pnew;  //tree 指向根的頭結點//第一個結點 即是隊列頭也是 隊列尾phead = ptail = listpnew;pre = listpnew; //  用來判斷當前結點 的左右孩子是否滿了}else {//元素直接入隊ptail ->pnext = listpnew;ptail =listpnew;//接下來把元素放入樹中if(pre->p->lchild ==NULL){pre ->p ->lchild =pnew;  // pre -> p 左孩子為空 就放入左孩子}else if(pre->p->rchild==NULL){pre->p->rchild =pnew;pre = pre->pnext;  // !!! 左右孩子都滿了，指向下一個節點}}}puts("前序");PreOrder(tree);printf("\n");puts("中序");InOrder(tree);printf("\n");puts("后序");PostOrder(tree);printf("\n");LevelOrder(tree);return 0;//這沒有對樹進行相應的輸出  ，使用調試發現建樹完成}//abcdefg//        前序//abdecfg//        中序//dbeafcg//        后序//debfgca//        層序//abcdefg

這個代碼實現了通過層次輸入字符數據來構建一棵二叉樹，并對這棵二叉樹進行前序、中序、后序、層序遍歷，完整地展示了樹的構建與遍歷過程。

---

? 具體功能如下：

1. 層次建樹（用輔助隊列實現）

• 利用自定義的tag_t 輔助隊列結構體進行層次建樹。
• 每次輸入一個字符就創建一個二叉樹結點。
• 如果當前樹為空（即首次輸入），設置為根節點；
• 后續的結點依次作為上一結點的左孩子、右孩子插入；
• 每插入完一個結點，就將其作為隊列中的一個元素排隊，繼續等待為它的孩子分配子節點。

📘寫在最后

學習數據結構尤其是二叉樹，最重要的是掌握“結構 + 操作”的關系。每一次遍歷、每一次入隊出隊，背后都是指針、結構體、遞歸這些基礎能力的體現。希望本文結合實際代碼的講解能為你的學習提供實用幫助。