?深度學習是人工智能的一種實現方法。本章我們將考察作為深度學習的代表的卷積神經網絡的數學結構。

5-1小惡魔來講解卷積神經網絡的結構

深度學習是重疊了很多層的隱藏層（中間層）的神經網絡。這樣的神經網絡使隱藏層具有一定的結構，從而更加有效地進行學習。本節我們就來考察一下近年來備受關注的卷積神經網絡的設計思想。

使網絡具有結構

卷積神經網絡是當下正流行的話題，尚且難以總結一般理論。這里，我們利用一個最簡單的例題來考察一下卷積神經網絡的思想。如下所示，這個例題是由前面考察過的例題整理而成的，它雖然簡單，但是能夠很好地幫助我們理解卷積神經網絡的結構。

例題建立一個卷積神經網絡，用來識別通過6×6像素的圖像讀取的手寫數字1、2、3。圖像的像素為單色二值。

首先，我們來介紹一下作為這個例題的解答的卷積神經網絡的示例，如下頁的圖所示。

圖中用圓圈將變量名圈起來的就是神經單元，從這個圖中我們可以了解到卷積神經網絡的特點。隱藏層由多個具有結構的層組成。具體來說，隱藏層是多個由卷積層和池化層構成的層組成的。它不僅“深”，而且含有內置的結構。

注：卷積層的英文是convolution?layer。這里展示的是最原始的卷積神經網絡，實際的網絡更為復雜。

思路

人們是如何想到這樣的結構的呢？如果我們了解了卷積神經網絡的思路，就可以在各種領域中進行應用。這里我們也同樣請第1章登場的“惡魔”來講解。

在1-5節考察過的神經網絡中，住在隱藏層的惡魔具有各自偏好的模式。惡魔對自己偏好的模式做出反應，輸出層接收這些信息，從而使神經網絡進行模式識別成為可能。

本節登場的惡魔與之前的惡魔性格稍微有點不同。雖然他們的共同點都是具有自己偏好的模式，但是相比第3章登場的惡魔坐著一動不動，這里的惡魔是活躍的，他們會積極地從圖像中找出偏好的模式，我們稱之為小惡魔。

為了讓這些小惡魔能夠活動，我們為其提供工作場所，那就是由卷積層與池化層構成的隱藏子層。我們為每個小惡魔準備一個隱藏子層作為工作場所。

提供能讓小惡魔活動的工作場所（外側的框）。這個隱 藏子層的編號為 1。

活躍的小惡魔積極地掃描圖像，檢查圖像中是否含有自己偏好的模式。如果圖像中含有較多偏好的模式，小惡魔就很興奮，反之就不興奮。此外，由于偏好的模式的大小比整個圖像小，所以興奮度被記錄在多個神經單元中。

小惡魔掃描圖像數據，根據檢測到的偏好模式的多少而產生興奮，其興奮度會被記錄在卷積層的神經單元中。神經單元名中F1的F為Filter的首字母，1為隱藏子層的編號。

注：一般用于掃描的過濾器的大小是5×5。這里為了使結果變簡單，我們使用如圖所示的3×3的大小。

活躍的小惡魔進一步整理自己的興奮度，將興奮度集中起來，整理后的興奮度形成了池化層。

池化層的建立。小惡魔將掃描結果的興奮度（等）進一步集中起來，整理為池化層的神經單元。池化層中濃縮了小惡魔所偏好的模式的信息。神經單元名中P1的P為Pooling的首字母，1為隱藏子層的編號。

因此，池化層的神經單元中濃縮了作為考察對象的圖像中包含了多少小惡魔所偏好的模式這一信息。

1-5節介紹的惡魔每人有一個偏好模式，本節的小惡魔每人也只有一個偏好模式。因此，要識別數字1、2、3，就需要讓多個小惡魔登場。這里我們比較隨意地假定有3個小惡魔。輸出層將這3個小惡魔的報告組合起來，得出整個神經網絡的判定結果。

與第1章相同，輸出層里也住著3個輸出惡魔，這是為了對手寫數字1、2、3分別產生較大反應。

輸出層將3個小惡魔的報告進行匯總。為了分別對手寫數字1、2、3產生較大反應，需要3個輸出惡魔。

以上就是利用小惡魔來解答例題的方法。卷積神經網絡就是按照這一思路建立神經網絡的卷積層和池化層的。

如前所述，第1章登場的隱藏層的惡魔是靜態的，他們只是觀察數據然后做出反應。而本章的小惡魔是動態的，他們會積極地掃描圖像，整理興奮度并向上一層報告。由于這些小惡魔的性格特點，卷積神經網絡產生了我們前面學習過的簡單神經網絡所沒有的優點。

????????①對于復雜的模式識別問題，也可以用簡潔的網絡來處理。

????????②整體而言，因為神經單元的數量少了，所以計算比較輕松。

而卷積神經網絡之所以在各種領域備受矚目，也是得益于這樣的性質。

此外，目前為止我們的討論都是假定小惡魔住在神經網絡的隱藏層。

和所有的科學理論一樣，模型是否正確，取決于用它做出的預測是否能夠很好地解釋現實情況。眾所周知，現在卷積神經網絡已經有了一些顯著的成果，例如能夠識別出YouTube上的貓的圖像等。

那么，神經網絡是如何實現這里考察的小惡魔的活動的呢？我們將在下一節考察數學上的實現方法。

小惡魔的人數

在前面的說明中，登場的小惡魔一共有3人。這里的人數不是預先確定的。如果我們預估用5個模式能夠區分圖像，那么就需要有5個小惡魔。這樣一來，我們就應當準備好5個由卷積層和池化層形成的隱藏子層。

如果圖像變得復雜，卷積層和池化層形成的隱藏子層的數目也相應地增加。對于需要多少個隱藏子層等問題，往往需要進行反復試錯來確定。

而且，在識別貓的圖像的情況下，隱藏層的結構本身也需要變得更復雜。這就是深度學習的設計人員可以大展身手的地方。

5-2將小惡魔的工作翻譯為卷積神經網絡的語言

我們在5-1節考察了卷積神經網絡的思路。通過設想能夠尋找偏好模式的活躍的小惡魔，從而理解了卷積神經網絡的設計思想。本節我們來看看如何將小惡魔的工作替換為數學計算。這里考察的例題與上一節相同。

例題建立一個神經網絡，用來識別通過6×6像素的圖像讀取的手寫數字1、2、3。圖像像素為單色二值。

從數學角度來考察小惡魔的工作

下面我們從數學角度來考察5-1節的小惡魔的工作。首先我們請小惡魔S登場。假定這個小惡魔S喜歡如下的模式S。

注：模式的大小通常為5×5。這里為了使結果變簡單，我們使用圖中所示的小的3×3模式。

假設下面的圖像“2”就是要考察的圖像。我們將手寫數字2作為它的正解。

圖像“2”。從數學角度考察小惡魔處理這個圖像的過程。

小惡魔S首先將偏好的模式S作為過濾器對圖像進行掃描。我們將這個過濾器命名為過濾器S。接下來，我們實際用過濾器S掃描整個圖像“2”。

各個圖像下面的“相似度”表示過濾器S的灰色格子部分與掃描圖像塊的灰色格子部分吻合的地方的個數。這個值越大，就說明越符合小惡魔偏好的模式。

注：這個相似度是像素為單色二值（即0與1）時的情況，關于更一般的模式的相似度，我們將在附錄C中討論。

我們將這個相似度匯總一下，如下表所示。這就是根據過濾器S得到的卷積（convolution）的結果，稱為特征映射（feature?map）。

這就是在5-1節登場的小惡魔執行的掃描結果。

注：這樣的過濾器的計算稱為卷積。

卷積層中的神經單元將這一卷積的結果作為輸入信息。各神經單元將對應的卷積的值加上特征映射固有的偏置作為加權輸入（下圖）。

卷積層的神經單元的加權輸入。請注意偏置b是相同的。此外，小惡魔S在編號1的隱藏子層中活動。

卷積層的各個神經單元通過激活函數來處理加權輸入，并將處理結果作為神經單元的輸出。這樣卷積層的處理就完成了。

卷積層神經單元通過激活函數將加權輸入轉換為輸出

通過池化進行信息壓縮

這個例題的卷積層神經單元數目比較少，因此可以簡單地列出輸出值。不過，在實際圖像的情況下，卷積層神經單元的數目是十分龐大的。因此，就像5-1節提到的那樣，需要進行信息壓縮操作，然后將壓縮結果放進池化層的神經單元中。

壓縮的方法十分簡單，只需要將卷積層神經單元劃分為不重疊的2×2的區域，然后在各個區域中計算出代表值即可。本文中我們使用最有名的信息壓縮方法最大池化（max pooling），具體來說就是將劃分好的各區域的最大值提取出來。

最大池化的結果。池化層的輸入和輸出為相同的值。

注：池化操作通常在2×2的區域中進行，但也并非一定這樣。

這樣一來，一張圖像的信息就被集中在緊湊的神經單元集合中了。

我們通過下面的例子來復習上述計算過程。

例利用前面所示的圖像“2”和過濾器S來實際計算卷積層和池化層中神經單元的輸入輸出值。設特征映射的偏置為-1（閾值為1），激活函數為Sigmoid函數。

按照下圖的順序進行計算，如下所示。

注：池化層的輸入和輸出相同。為了簡化，神經單元也用方框表示。

問題與前面例的一樣，計算用過濾器S處理下邊的圖像“1”和“3”時卷積層和池化層中神經單元的輸入輸出值。

解按照與例相同的步驟，可以得到如下圖所示的結果。

注：這里為了簡化，神經單元也用方框表示。

從上面的例和問題可以了解到，數字“2”的圖像的池化結果是由比數字“1”“3”的圖像的池化結果大的值構成的。如果池化層神經單元的輸出值較大，就表示原始圖像中包含較多的過濾器S的模式。由此可知，過濾器S對手寫數字“2”的檢測發揮了作用。此外，做出判斷的是輸出層。與我們在第1～4章考察的神經網絡一樣，輸出層將上一層（池化層）的信息組合起來，并根據這些信息得出整個網絡的判斷結論。

如上所示，我們將5-1節考察的小惡魔的工作通過數學思路表現了出來。然而，只有數學思路還不能進行計算。在下一節，為了能夠實際進行計算，我們會將這些思路用數學式子表示出來。

5-3卷積神經網絡的變量關系式

要確定一個卷積神經網絡，就必須具體地確定過濾器以及權重、偏置。為此，我們需要用數學式來表示這些參數之間的關系。

確認各層的含義以及變量名、參數名

與前面一樣，我們通過下面的例題進行討論。

例題建立一個神經網絡，用來識別通過6×6像素的圖像讀取的手寫數字1、2、3。圖像像素為單色二值。學習數據為96張圖像。

在5-1節中，作為解答示例，我們展示了如下的卷積神經網絡的圖。

我們把確定這個卷積神經網絡所需的變量、參數的符號及其含義匯總在下表中。

位置	符號	含義
輸入層		神經單元中輸入的圖像像素（i行j列）的值。與輸出值相同
過濾器		用于建立第k個特征映射的過濾器的i行j列的值。這里為了簡化，考慮3×3大小的過濾器（通常采用5×5大小）
卷積層		卷積層第k個子層的i行j列的神經單元的加權輸入
		卷積層第k個子層的i行j列的神經單元的偏置。注意這些偏置在各特征映射中是相同的
		卷積層第k個子層的i行j列的神經單元的輸出（激活函數的值）
池化層		池化層第k個子層的i行j列的神經單元的輸入。通常是前一層輸出值的非線性函數值
		池化層第k個子層的i行j列的神經單元的輸出。與輸入值 zij(P)k一致
輸出層		從池化層第k個子層的i行j列的神經單元指向輸出層第n個神經單元的箭頭的權重
		輸出層第n個神經單元的加權輸入
		輸出層第n個神經單元的偏置
		輸出層第n個神經單元的輸出（激活函數的值）
學習數據		正解為1時，t1=1，t2=0，t3=0正解為2時，t1=0，t2=1，t3=0正解為3時，t1=0，t2=0，t3=1

這些變量和參數的位置關系如下圖所示。

注：圖中的標記遵循3-1節的約定。

與神經網絡不同的是，卷積神經網絡中考慮的參數增加了過濾器這個新的成分。

接下來，我們會逐層考察在今后的計算中所需的參數和變量的關系式。雖然有些內容與5-1節、5-2節有所重復，但我們要從數學上一般化的角度來弄清楚。請讀者對照著5-1節、5-2節閱讀，并嘗試理解數學式。

輸入層

在例題中，輸入數據是6×6像素的圖像。這些像素值是直接代入到輸入層的神經單元中的。這里我們用xij表示所讀入的圖像的i行j列位置的像素數據，并把這個符號用在輸入層的變量名和神經單元名中。

輸入層神經單元的位置與對應圖像的像素位置一致。

在輸入層的神經單元中，輸入值和輸出值相同。如果將輸入層i行j列的神經單元的輸出表示為，那么以下關系式成立（a的上標I為Input的首字母）。

過濾器和卷積層

就像5-1節、5-2節所考察的那樣，小惡魔通過3×3大小的過濾器來掃描圖像。現在，我們準備3種過濾器（5-1節）。此外，由于過濾器的數值是通過對學習數據進行學習而確定的，所以它們是模型的參數。如下圖所示，這些值表示為,…（k=1,2,3）。

構成過濾器的數值是模型的參數。此外，F為Filter的首字母。

注：過濾器也稱為核（kernel）。

過濾器的大小通常為5×5。本書中為簡單起見，使用更為緊湊的3×3大小。此外，也不是必須準備3種過濾器。當計算結果與數據不一致時，我們需要更改這個數目。

現在，我們利用這些過濾器進行卷積處理（5-2節）。例如，將輸入層從左上角開始的3×3區域與過濾器1的對應分量相乘，得到下面的卷積值（c為convolution的首字母）。

這就是5-2節中稱為“相似度”的值。

依次滑動過濾器，用同樣的方式計算求得卷積值。這樣一來，我們就得到了使用過濾器1的卷積的結果。另外，關于這些數值的數學含義，請參照附錄C。

一般地，使用過濾器k的卷積的結果可以如下表示。這里的i、j為輸入層中與過濾器對應的區域的起始行列編號（i、j為4以下的自然數）。

這樣得到的數值集合就形成特征映射。

我們給這些卷積值加上一個不依賴于i、j的數。

考慮以作為加權輸入的神經單元，這種神經單元的集合形成卷積層的一個子層。為卷積層共同的偏置。

激活函數為a(z)，對于加權輸入，神經單元的輸出可以如下表示。

式 (1)、式 (2) 中變量和參數的關系。圖 中是構成卷積層第1個子層的神經單元集合。各個神經單元的加權輸入為式 (1)，輸出為式 (2)。請注意它們具有共同的偏置。此外，這個圖的標記遵循3-1節的約定。

問題試著寫出卷積層第1個子層的1行2列的神經單元的加權輸入與輸出的式子。激活函數為Sigmoid函數。

池化層

卷積神經網絡中設置有用于壓縮卷積層信息的池化層。在5-1節、5-2節中，我們把2×2個神經單元壓縮為1個神經單元，這些壓縮后的神經單元的集合就形成了池化層。

池化層的信息壓縮方法。這里考察的卷積層由4×4個神經單元構成，分別使其中的2×2個為1組壓縮為1個。

很多文獻也和這里一樣，將特征映射的2×2個神經單元壓縮為1個神經單元。通過執行一次池化操作，特征映射的神經單元數目就縮減到了原先的四分之一。

注：如前所述，并非必須是2×2大小。

壓縮的方法有很多種，比如較為有名的最大池化法，例如像下圖這樣，從4個神經單元的輸出a11、a12、a21、a22中選出最大值作為代表。

例1下圖左邊為卷積層的輸出值，右邊為最大池化的結果。

從神經網絡的觀點來看，池化層也是神經單元的集合。不過，從計算方法可知，這些神經單元在數學上是非常簡單的。通常的神經單元是從前一層的神經單元接收加權輸入，而池化層的神經單元不存在權重和偏置的概念，也就是不具有模型參數。

此外，由于輸入和輸出是相同的值，所以也不存在激活函數的概念。從數學上來說，激活函數a(x)可以認為是恒等函數a(x)=x。這個特性與輸出層的神經單元相似。

池化層由神經單元構成， 但它們與通常的神經單元不同。

以上討論的池化層的性質可以用式子如下表示。這里，k為池化層的子層編號，i、j為整數，取值必須使得它們指定的參數有意義。

池化層的神經單元所接收的輸入中沒有權重和偏置的概念。激活函數可以認為是a(x)=x，例如

輸出層

為了識別手寫數字1、2、3，我們在輸出層中準備了3個神經單元。與第3章和第4章中一樣，它們接收來自下一層（池化層）的所有神經單元的箭頭（即全連接）。這樣就可以綜合地考察池化層的神經單元的信息。

池化層的神經單元和輸出層的神經單元是全連接。圖中的神經單元名使用了輸出變量名（共有12×3個箭頭，這里省略）。

我們將這個圖用式子來表示。輸出層第n個神經單元（n=1,2,3）的加權輸入可以如下表示。

這里，系數為輸出層第n個神經單元給池化層神經單元的輸出（k=1,2,3；i=1,2；j=1,2）分配的權重，bn(O)為輸出層第n個神經單元的偏置。

例2我們來具體地寫出的式子。

上式中變量和參數的關系如下圖所示。

為了寫出而用到的變量和參數的關系的簡略圖。

我們來考慮輸出層神經單元的輸出，它們形成了整個卷積神經網絡的輸出。輸出層第n個神經單元的輸出值為，激活函數為a(z)，則

（n=1,2,3）中最大值的下標n就是我們要判定的數字。

求代價函數Ct

現在我們考慮的神經網絡中，輸出層神經單元的3個輸出為，對應的學習數據的正解分別記為t1、t2、t3（參考3-3節，以及本節開頭的表）。于是，平方誤差C可以如下表示。

注：系數1/2是為了簡潔地進行導數計算，不同的文獻可能會使用不同的系數，這個系數對結論沒有影響。此外，關于平方誤差，請參考2-12節、3-4節。

本文采用平方誤差作為誤差函數。正解變量t1在讀取數字圖 像“1”時為1，在其他情況下為0；正解變量t2在讀取數字圖像“2”時為1，在其他情況下為0；正解變量t3在讀取數字圖像“3”時為1，在其他情況下為0。

將輸入第k個學習圖像時的平方誤差的值記為Ck，如下所示。

注：關于變量中附帶的[k]，請參考3-1節。

全體學習數據的平方誤差的總和就是代價函數CT。因此，我們現在考慮的神經網絡的代價函數CT可以如下求出。

注：96為例題中學習圖像的數目。

這樣我們就得到了作為計算的主角的代價函數Ct。數學上的目標是求出使代價函數Ct達到最小的參數，即求出使代價函數Ct達到最小的權重和偏置，以及卷積神經網絡特有的過濾器的分量，如下圖所示。

數學上的目標是實現參數的最優化。確定權重、偏置以及過濾器分量的原理與回歸分析相同。使代價函數CT達到最小的參數是最優參數，而這樣的思路就是最優化。

通過計算確認模型的有效性

前面我們已經多次提到過，要確認目前建立的卷積神經網絡是否有助于數據分析，就要實際使用這個模型進行計算，看得到的結果是否能夠很好地解釋給定的數據。

下一節，為了確認前面討論的內容，我們將使用Excel的最優化工具（求解器），直接將代價函數最小化，并求出使函數達到最小時的過濾器、權重和偏置。

備 注 L2池化

本節我們采用了最大池化作為池化的方法。最大池化具體來說就是使用 對象區域的最大值作為代表值的信息壓縮方法。除了最大池化之外，還有其 他池化方法，如下所示。

名　稱	說　明
最大池化	使用對象區域的最大值作為代表值的壓縮方法
平均池化	使用對象區域的平均值作為代表值的壓縮方法
L2 池化	例如，對于4個神經單元的輸出值a1、a2、a3、a4，使用? 作為代表值的壓縮方法

5-4用Excel體驗卷積神經網絡

本節我們通過Excel來確認一下前面考察的卷積神經網絡能否實際地發揮作用。

用Excel確定卷積神經網絡

對于下面的例題，我們用Excel來確定卷積神經網絡。

例題對于在5-3節的例題中考察的卷積神經網絡，確定它的過濾器、權重和偏置。學習數據的96張圖像實例收錄在附錄B中。

注：代價函數使用平方誤差C的總和，激活函數使用Sigmoid函數，池化方法使用最大池化。

接下來，我們逐個步驟地進行計算。

①讀入學習用的圖像數據

為了讓卷積神經網絡進行學習，需要用到學習數據。因此，我們將圖像讀入到工作表中，如下圖所示。

如上圖所示，將數字圖像保存在工作表中。

由于圖像是單色二值圖像，我們將圖像的灰色部分設置為1，白色部分設置為0，將正解代入到變量t1、t2、t3中。學習圖像為數字1時t1=1，圖像為數字2時t2=1，圖像為數字3時t3=1，其他情況下變量值為0。

此外，學習用的圖像數據全部存放在計算用的工作表中，如下圖所示。

注：如圖中P列、Q列所示，圖像最右邊的2列像素縮小了顯示寬度。

②設置參數的初始值

我們來設置過濾器、權重和偏置的初始值。這里使用了標準正態分布隨機數（2-1節）。

注：當求解器的執行結果不收斂時，要修改初始值。

③從第1張圖像開始計算各種變量的值

根據當前的過濾器、權重和偏置，對于第1張圖像，計算出各個神經單元的加權輸入值、輸出值和平方誤差C的值。計算時利用5-3節的關系式。

④復制步驟③中建立的各個函數到所有數據中

將處理第1張圖像時嵌入的各個函數復制到其他圖像數據中，直到最后一個圖像實例（該例題中為第96張）為止。

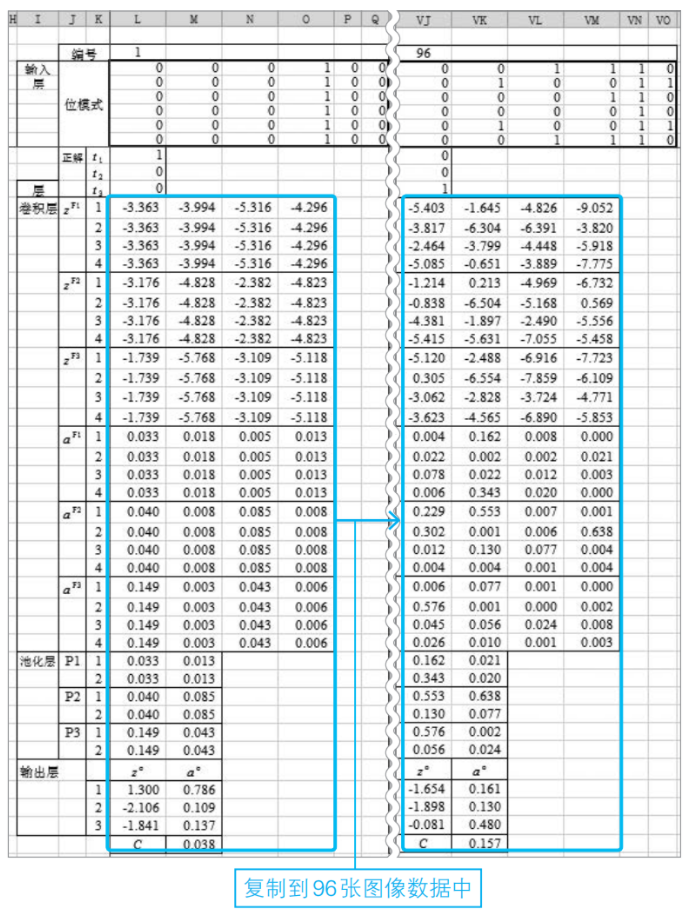
將處理第1張圖像時嵌入的各個函數復制到所有學習數據中（96張圖像）。

⑤算出代價函數Ct的值

利用5-3節的式(7)求出代價函數Ct的值。

⑥利用求解器執行最優化

利用Excel的標準插件求解器，計算出代價函數CT的最小值。如下圖所示，設置單元格地址，并運行求解器。

測試

為了確認步驟⑥中得到的過濾器、權重和偏置確定的卷積神經網絡是否能正確地工作，我們試著輸入新的數據，例如下邊的圖像。卷積神經網絡的判斷結果是數字“1”，這與人類的直觀感受一致。

這個例子中輸入了與字母I相似的數字1的圖像。盡管如此，判定結果也是1。

5-5卷積神經網絡和誤差反向傳播法

第4章我們考察了多層神經網絡的誤差反向傳播法的結構及其計算方法。本節我們來考察卷積神經網絡的誤差反向傳播法的結構。其實它在數學上的結構與誤差反向傳播法相同。我們通過下面這個之前考察過的具體例子進行討論。

例題建立一個神經網絡，用來識別通過6×6像素的圖像讀取的手寫數字1、2、3。過濾器共有3種，其大小為3×3。圖像像素為單色二值，學習數據為96張圖像。

確認關系式

對于這個例題，我們建立了如下圖所示的卷積神經網絡并進行了講解。接下來，我們來匯總一下前面考察過的關于這個網絡的關系式。

注：神經單元的名稱使用了輸出變量名。

●卷積層

k為卷積層的子層編號，i、j（i,j=1,2,3,4）為掃描的起始行、列的編號，有以下關系式成立（5-3節式(1)、式(2)）。a(z)表示激活函數。

●池化層

k為池化層的子層編號（k=1,2,3），i、j為該子層中神經單元的行、列編號（i,j=1,2），有以下關系式成立（這里是最大池化的情況，參考5-3節式(3)）。

注：Max函數輸出（）內最大項的值。

●輸出層

n為輸出層神經單元的編號（n=1,2,3）（5-3節式(4)、式(5)），有以下關系式成立。a(z)表示激活函數。

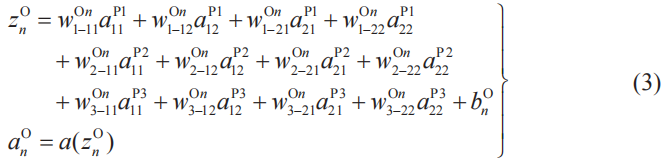
●平方誤差

t1、t2、t3為表示學習數據正解的變量，C為表示平方誤差的變量，有以下關系式成立（5-3節式(6)）。

梯度下降法是基礎

第4章中應用了梯度下降法來確定神經網絡的參數。同樣地，在確定卷積神經網絡的參數時，梯度下降法也是基礎。以CT為代價函數，梯度下降法的基本式可以如下表示（2-10節）。

式子右邊的括號中為代價函數CT的梯度。如式(5)所示，這里以關于過濾器的偏導數、關于權重的偏導數，以及關于偏置的偏導數作為分量（共69個分量）。

代價函數CT的梯度

正如第4章中考察的那樣，這個梯度的偏導數計算非常麻煩。因此，人們想出了誤差反向傳播法，具體來說就是將梯度分量的偏導數計算控制到最小限度，并通過遞推關系式進行計算。

省略變量符號中附帶的圖像編號

從式(5)可以看出，代價函數CT是梯度計算的目標。把從學習數據的

第k張圖像得到的平方誤差式(4)的值記為Ck，代價函數CT可以如下求出。

從式(6)中也可以看出，代價函數CT是從學習數據的各個圖像得到的平方誤差式(4)的和。我們在4-1節考察過，求代價函數CT的偏導數時，先對式(4)求偏導數，然后代入圖像實例，并對所有學習數據求和就可以了。因此，從現在開始，我們考慮以式(4)為對象的代價函數的計算。

例1求式(5)右邊的梯度分量時，如果先求式(6)的CT再求偏導數，就會浪費不少工夫。首先計算式(4)的平方誤差C的偏導數，然后將圖像實例代入式中，算出［k=1,2,…,96（96為全部圖像的數目）］，最后對全部數據進行求和就可以了。這樣極大地減少了偏導數的計算次數。

之后我們將按照例1的方法進行計算。因此，除了必要的情況之外，不再將圖像編號表現在關系式中。

符號δj(l)的導入及偏導數的關系

與第4章一樣，我們在誤差反向傳播法中導入名為神經單元誤差的δ符號。現在我們考察的例題中，神經單元誤差δ有兩種：一種是的形式，表示卷積層第k個子層的i行j列的神經單元誤差；另一種是的形式，表示輸出層第n個神經單元的誤差。與第4章一樣，這些δ符號是通過關于加權輸入、（式(1)、式(3)）的偏導數來定義的。

例2(卷積層第1個子層的1行1列的神經單元的誤差）

(輸出層第1個神經單元的誤差）

例2的變量的位置關系（神經單元的表示請參考3-1節）。

與第4章的神經網絡的情況一樣，平方誤差C關于參數的偏導數可以通過這些神經單元誤差δ簡潔地表示。接下來，我們來考察這個事實。

用δj(l)表示關于輸出層神經單元的梯度分量

利用式(3)、式(7)和偏導數鏈式法則（2-8節），我們可以進行下面的例3、例4的計算。

例3

例4

例3的變量和參數的關系圖。

我們可以將例3、例4一般化為如下的式(8)。這里，n為輸出層的神經單元編號，k為池化層的子層編號，i、j為過濾器的行、列編號（i,j=1,2）。

用δj(l)表示關于卷積層神經單元的梯度分量

下面我們來考察關于卷積層神經單元的梯度分量。這里取過濾器分量w1(F)11的偏導數作為例子。首先，根據式(1)，有

利用這些式子，可以得到下式。

根據鏈式法則，有

把δ的定義式(7)和式(9)代入式(10)中，得到

式(11)的右邊第一項和最后一項的變量關系圖。

我們可以很容易地將式(11)擴展到過濾器的其他分量。設k為過濾器的編號（這里與卷積層的編號相同），i、j為過濾器的行、列編號（i、j=1,2,3），將上式進行一般化，如下所示。

注：這是像素數為6×6、過濾器大小為3×3時的關系式。在其他情況下，需要根據實際情況對該式進行相應的改變。

此外，代價函數關于卷積層神經單元的偏置的偏導數可以如下求得。卷積層各個子層的所有神經單元的偏置都是相同的，例如對于第一個特征映射來說，可以得到下面的關系式。這與式(12)是一樣的。

式(13)可以如下進行推廣，其中k為卷積層的子層編號。簡而言之，代價函數關于卷積層神經單元的偏置的偏導數，就是卷積層各個子層的所有神經單元誤差的總和。

注：這是像素數為6×6、過濾器大小為3×3時的式子。在其他情況下，需要根據實際情況對該式進行相應的改變。

像這樣，由式(8)、式(12)和式(14)可知，如果能求出神經單元誤差δ,就可以求出式(5)的所有梯度分量。因此我們的下一個課題就是計算由式(7)定義的神經單元誤差δ。

計算輸出層的δ

與簡單的神經網絡（4-3節）的情況一樣，計算神經單元誤差δ也是利用數列的遞推關系式（2-2節）。首先求出輸出層的神經單元誤差δ,接著通過遞推關系式反向地求出卷積層的神經單元誤差δ。

下面我們先來求輸出層的神經單元誤差δ。激活函數為a(z)，n為該層的神經單元編號，根據定義式(7)，有

根據式(4)，有

將式(16)代入到式(15)中，就得到了輸出層的神經單元誤差δ。

建立關于卷積層神經單元誤差δ的“反向”遞推關系式

與神經網絡的情況一樣（4-3節），接下來要做的就是建立“反向”遞推關系式。我們以δ11(F)1為例進行考察。根據偏導數的鏈式法則，有

式(18)的右邊的變量關系圖。

把式(18)中的公因式提取出來，就可以像下面這樣進行簡化。

根據式(3)，有

再根據式(2)，有

根據式(21)中的，可得

此外，由于在進行池化時形成一個區塊，所以的偏導數可以如下表示。

由于也可以記為，把δ的定義式(7)以及式(20)～(23)

代入式(19)，可得

其他的神經單元誤差也可以用同樣的方式進行計算，因此上式可以推廣如下。

這里，k、i、j等的含義與前面相同。此外，i′、j′表示卷積層i行j列的神經單元連接的池化層神經單元的位置。

例5

例5中出現的變量的關系。

這樣我們就得到了輸出層和卷積層中定義的神經單元誤差δ的關系式（也就是遞推關系式）。輸出層的神經單元誤差δ已經根據式(17)得到了，因此利用關系式(25)，即使不進行導數計算，也可以求得卷積層的神經單元誤差δ。這就是卷積神經網絡的誤差反向傳播法的結構。

誤差反向傳播法的結構。只要求出輸出層的神經單元誤差δ,就可以簡單地求出卷積層的神經單元誤差δ。

問題證明例5的關系式。 解與式(24)的證明一樣，如下所示。 這樣就得到了例5的式子。

5-6用Excel體驗卷積神經網絡的誤差反向傳播法

與第4章中考察的神經網絡一樣，在卷積神經網絡中也可以利用誤差反向傳播法。下面我們利用前面考察過的以下例題，用Excel實際地進行計算。

注：計算步驟與4-4節相同。

例題對于5-5節中考察的卷積神經網絡，我們來確定它的過濾器、權重、偏置的值。學習數據的96張圖像實例收錄在附錄B中。激活函數使用Sigmoid函數。

作為解答示例的神經網絡請參考5-1節，變量和參數的關系式請參考5-5節。現在，我們來進行具體的計算。

①讀入學習用的圖像數據

為了讓卷積神經網絡進行學習，需要用到學習數據。因此，與5-4節的步驟①同樣地讀入圖像數據。

②設置過濾器分量、權重和偏置的初始值

現在的過濾器分量、權重和偏置當然是未知的，需要以初始值為出發點來求出。因此，我們利用正態分布隨機數（2-1節）來設置初始值。

此外還要設置小的正數作為學習率η。

備 注 學習率η的設置

就像第4章中考察的那樣，在設置學習率η時需要進行反復試錯。如果η過小，則代價函數Ct不能迅速地達到最小值，也可能掉進意料之外的極小值處。反之，如果η過大，則存在代價函數Ct不收斂的風險。我們的目標是 將代價函數Ct最小化，為了使 Ct的值變得充分小，需要嘗試各種不同的值來計算。

③算出神經單元的輸出值以及平方誤差C

對于第1張圖像，利用當前給出的過濾器分量、權重和偏置的值來求出各個神經單元的加權輸入、激活函數的值以及平方誤差C。

④根據誤差反向傳播法計算各層的神經單元誤差δ

首先，計算輸出層的神經單元誤差（5-5節式(17)）。接著，根據“反向”遞推關系式計算（5-5節式(25)）。

⑤根據神經單元誤差計算平方誤差C的偏導數

根據步驟④中求出的δ,計算平方誤差C關于過濾器、權重和偏置的偏導數。

⑥計算代價函數Ct及其梯度▽Ct

到目前為止，我們以第1張圖像作為學習數據的代表進行了考察。我們的目標是把前面的計算結果對全部數據加起來，得到代價函數CT及其梯度值。因此，必須把前面建立的工作表復制到全部學習數據的96張圖像上。

對96張圖像復制完畢之后，將平方誤差C，以及步驟⑤中求得的平方誤差C關于參數的偏導數加起來，這樣就算出了代價函數的值和梯度（5-5節式(6)）。

⑦根據⑥中求出的梯度，更新權重和偏置的值

利用梯度下降法的基本式（5-5節式(5)），更新過濾器、權重和偏置（2-10節）。為此，在上述⑥的工作表下面建立新的工作表，計算出更新值。

⑧反復進行③~⑦的操作

利用⑦中算出的新的權重w和偏置b，再次執行從③開始的處理。把這樣算出的第2次處理的塊狀區域復制49份到下面，進行50次計算。

把從60行到120行的塊狀區域復制49份到下面。

通過以上步驟，計算就結束了。我們來看看代價函數CT的值。

代價函數Ct=0.497

由于學習數據由96張圖像構成，每張圖像平均為0.005。根據平方誤差的函數（5-5節式(4)），每張圖像的最大誤差為3/2=1.5，因此可以說以上步驟算出的是一個很好的結果。

用新的數字來測試

我們創建的神經網絡是用于識別手寫數字1、2、3的。我們來確認一下實際上它能否正確識別數字。下面的Excel工作表是利用步驟⑧中得到的參數并輸入右邊的圖像進行計算的例子。判定結果為數字“3”。

備 注 跟蹤代價函數CT的值

跟蹤50次代價函數的計算結果，就可以實際理解梯度下降法的含義。 從邏輯上看，代價函數 Ct 的值當然是隨著每次迭代而減小。第 4 章中我們已經考察過，梯度下降法的優點就是減小的速度是最快的。

不過，用計算機執行誤差反向傳播法時，也存在代價函數Ct不減小的情況。就像第4章中考察的那樣，可以認為原因是學習率和初始值不合適。在這種情況下，可以修改學習率和初始值重新進行計算。