從對數變換到深度框架：邏輯回歸與交叉熵的數學原理及PyTorch實戰

前言
?一、連乘變連加
二、最小化損失函數
2.1交叉熵
2.2 二分類交叉熵
2.3 多分類交叉熵
三、邏輯回歸與二分類
3.1 邏輯回歸與二分類算法理論講解
3.1.1 散點輸入
3.1.2 前向計算
3.1.3 Sigmoid函數引入
3.1.4 參數初始化
3.1.5 損失函數
3.1.6 開始迭代
3.1.7 梯度下降顯示
四、基于框架的邏輯回歸
4.1實驗原理
4.1.1 數據輸入
4.1.2 定義前向模型
4.1.3 定義損失函數和優化器
4.1.4 更新模型參數并顯示
4.1.5?pytroch 實現 sigmoid +二元交叉熵代碼?
4.1.6 softmax+多元交叉熵代碼
總結

前言

書接上文

深度學習激活函數與損失函數全解析：從Sigmoid到交叉熵的數學原理與實踐應用-CSDN博客文章瀏覽閱讀254次，點贊10次，收藏8次。本文系統探討了Sigmoid、tanh、ReLU、Leaky ReLU、PReLU、ELU等激活函數的數學公式、導數特性、優劣勢及適用場景，并通過Python代碼實現可視化分析。同時深入對比了極大似然估計與交叉熵損失函數的差異，闡述其在分類任務中的核心作用，揭示MSE在分類問題中的局限性及交叉熵的理論優勢。https://blog.csdn.net/qq_58364361/article/details/147440791?fromshare=blogdetail&sharetype=blogdetail&sharerId=147440791&sharerefer=PC&sharesource=qq_58364361&sharefrom=from_link

?一、連乘變連加

通過取對數(log的底數為e)，將連乘變成連加，方便計算。

將xi帶入得到如下公式：

對上面求導，然后通過求導數，令導數等于零來解方程，找到使得對數似然函數最大化的參數值p。

二、最小化損失函數

2.1交叉熵

交叉熵（Cross Entropy）是一種用于衡量兩個概率分布之間差異的度量方法。在機器學習中，交叉熵常用于衡量模型的預測結果與真實標簽之間的差異，交叉熵越小，兩個概率分布就越接近，即擬合的更好。

交叉熵的計算公式

通過上面的講解，發現對極大似然估計公式前面加上負號，使用負對數似然函數來定義損失函數和交叉熵公式一樣（通常稱為交叉熵損失函數），這樣就將最大化似然函數轉化為最小化損失函數的問題。這樣，在求解優化問題時，可以使用梯度下降等優化算法來最小化負對數似然函數（或交叉熵損失函數），從而得到最大似然估計的參數值。

2.2 二分類交叉熵

在二分類情況下，模型最后需要預測的結果只有兩種情況，對于每個類別我們的預測得到的概率為p和1-p,此時表示式為(log的底數為e):

N表示實驗次數也相當于樣本數

2.3 多分類交叉熵

多分類交叉熵就是對二分類的交叉熵的擴展，在計算公式中和二分類稍微有些區別，但是還是比較容易理解，具體公式如下所示：

補充：交叉熵怎么衡量損失的。

如果預測的概率值接近1 損失小，如果預測的概率值接近于0損失大，可以通過softmax(把數值轉換成概率)再結合交叉熵就能做分類損失函數。

三、邏輯回歸與二分類

從以下3個方面對邏輯回歸與二分類進行介紹
1.邏輯回歸與二分類算法理論講解
2.編程實例與步驟
3.實驗現象
上面這3方面的內容，讓大家，掌握并理解邏輯回歸與二分類。

3.1 邏輯回歸與二分類算法理論講解

這節學習邏輯回歸和二分類問題，在前面課程學了如何使用交叉熵這個損失函數來實現分類問題理論。

節就用一下交叉熵損失函數，來實現邏輯回歸的問題。

3.1.1 散點輸入

在本實驗中，給出了如下兩類散點，其分布如下圖所示：

輸入兩個值，一個是x1 ,x2 輸出是兩類一類是紅色點，一個是藍色點。

3.1.2 前向計算

本實驗中的前向計算與前面的所有章節都不同，因為本實驗的輸入特征是兩個，所以給出輸出公式為：

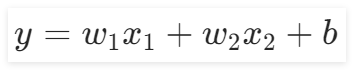
。在“前向計算”組件中，我們可以通過修改

的值來查看對應的直線。

3.1.3 Sigmoid函數引入

確定好線性函數公式之后，二分類的激活函數可以用Sigmoid和Softmax,這里使用Sigmoid函數作為它的輸出。

如下圖所示。

3.1.4 參數初始化

在“參數初始化”組件中，可以初始化兩個輸入特征、以及偏置b，還有學習率。由于輸入特征的增加，并且使用了激活函數激活，這里的學習率會比較大一點。

3.1.5 損失函數

在本實驗中，選用交叉熵損失函數作為損失函數。因為交叉熵比均方差更適合分類問題，而均方差比交叉熵更適合回歸問題。

在上一章節中，得到了交叉熵的表達式為：

將其激活后的函數帶入交叉熵中，得到：

wx+b能得到一個數值，這個數值經過Sigmoid就變成了概率，帶入交叉熵損失就能計算了。

3.1.6 開始迭代

反向傳播開始前，需要設置好迭代次數，本實驗提供了“開始迭代”組件，用來設置迭代次數，次數越高，模型的效果就越好。

接下來就是反向傳播的過程，其中參數的更新同樣使用的是梯度下降，也就意味著要令損失函數對參數進行求導，其結果如下圖所示：

推導一下

3.1.7 梯度下降顯示

接著通過“梯度下降顯示”組件顯示迭代過程中返回的參數值和損失值，該組件的內容如下圖所示：

代完成后，我們就可以通過這個模型來預測未知的數據屬于哪一類了。

import numpy as np
import matplotlib.pyplot as plt# 1.散點輸入
# 表示紅色點
class1_points = np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])
# 表示是綠色點
class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])
# 2提取兩類特征輸入維度為2
x1_data = np.concatenate((class1_points[:, 0], class2_points[:, 0]), axis=0)
x2_data = np.concatenate((class1_points[:, 1], class2_points[:, 1]), axis=0)
# 添加標簽
label = np.concatenate((np.zeros(len(class1_points)), np.ones(len(class2_points))), axis=0)
# 3參數初始化
w1 = 0.1
w2 = 0.2
b = 0
#超參數 學習率
lr = 0.05# sigmoid函數
def sigmoid(x):return 1 / (1 + np.exp(-x))  # 定義sigmoid函數，用于將線性回歸的輸出映射到[0,1]之間# 4.前向計算
def forward_cal(w1, w2, b):z = w1 * x1_data + w2 * x2_data + b  # 計算線性組合y_pre = sigmoid(z)  # 應用sigmoid函數得到預測值return y_pre# 5.計算損失函數
def loss_func(y_pre):loss = -np.mean(label * np.log(y_pre) + (1 - label) * np.log(1 - y_pre))  # 計算交叉熵損失return loss# 畫圖
fig, (ax1, ax2) = plt.subplots(2, 1)  # 創建一個包含兩個子圖的圖表
loss_list = []  # 用于存儲每輪迭代的損失值
epoch_list = []  # 用于存儲每輪迭代的epoch值
epochs = 1000  # 迭代總次數
for epoch in range(1, epochs + 1):  # 開始迭代y_pre = forward_cal(w1, w2, b)  # 前向傳播計算預測值loss = loss_func(y_pre)  # 計算損失deda = (y_pre - label) / (y_pre * (1 - y_pre))  # 計算損失函數的梯度dadz = y_pre * (1 - y_pre)  # 計算損失函數的梯度dzdw1 = x1_data  # 計算w1的梯度dzdw2 = x2_data  # 計算w2的梯度dzdb = 1  # 計算b的梯度gradient_w1 = np.dot(dzdw1, deda * dadz) / (len(x1_data))  # 計算w1的梯度gradient_w2 = np.dot(dzdw2, deda * dadz) / (len(x2_data))  # 計算w2的梯度gradient_b = np.mean(deda * dadz)  # 計算b的梯度w1 = w1 - lr * gradient_w1  # 更新w1w2 = w2 - lr * gradient_w2  # 更新w2b = b - lr * gradient_b  # 更新bprint(f"epoch:{epoch},loss:{loss}")  # 打印當前epoch和損失值loss_list.append(loss)  # 將損失值添加到列表中epoch_list.append(epoch)  # 將epoch值添加到列表中if epoch % 50 == 0 or epoch == 1:  # 每50輪迭代或初始迭代繪制一次圖形x1_min = x1_data.min()  # 計算x1數據的最小值x1_max = x1_data.max()  # 計算x1數據的最大值x2_min = -(w1 * x1_min + b) / w2  # 計算決策邊界的x坐標最小值x2_max = -(w1 * x1_max + b) / w2  # 計算決策邊界的x坐標最大值ax1.clear()  # 清空ax1ax1.scatter(x1_data[:len(class1_points)], x2_data[:len(class1_points)], color='r')  # 繪制紅色點ax1.scatter(x1_data[len(class1_points):], x2_data[len(class1_points):], color='b')  # 繪制藍色點ax1.plot([x1_min, x1_max], [x2_min, x2_max], color='r')  # 繪制決策邊界ax2.clear()  # 清空ax2ax2.plot(epoch_list, loss_list)  # 繪制損失隨epoch變化的曲線plt.pause(1)  # 暫停1秒

四、基于框架的邏輯回歸

4.1實驗原理

4.1.1 數據輸入

本實驗中，給出了如下兩類散點，其分布如下圖所示：

4.1.2 定義前向模型

準備好數據之后，接著就是定義前向過程，從上一章節可以知道，邏輯回歸算法實現分類時，有兩個輸入特征，即公式為：

。因此在“定義前向模型”組件中，需要保證輸入特征數量為2，輸出1個特征，使用Sigmoid()函數分成兩類，即

是一類，

是一類。

講解一下邏輯回歸+二元交叉熵和softmax+多分類交叉熵的區別？

邏輯回歸神經網絡示意圖

對計算出的結果結合二分類交叉熵進行計算損失。

eg: 實際標簽為 0，預測值a為0.1

計算方式：

eg: 實際標簽為 1，預測值a為0.8

softmax+普通交叉熵

輸出計算公式

將輸出的o1,o2,o3轉換成概率

使用softmax對輸出進行計算概率

對計算出的結果結合多分類交叉熵進行計算損失。

多分類交叉熵

多分類交叉熵就是對二分類的交叉熵的擴展，在計算公式中和二分類稍微有些區別，但是還是比較容易理解，具體公式如下所示：

onehot編碼

例子

比如分三類有貓、狗、牛三類，真實標簽是狗的話，可以表示為[0,1,0] onehot編碼。真實標簽是貓的話，可以表示為[1,0，0] onehot編碼，真實標簽是牛的話可以表示為[0,0,1]

4.1.3 定義損失函數和優化器

在選擇好前向模型后，需要接著選擇使用哪種損失函數和優化器，在“定義損失函數和優化器”組件中，提供的損失函數是交叉熵，優化器是SGD（隨機梯度下降），學習率有多個選項，比如0.5、0.1、0.05…，建議選擇較大的學習率，可以很快獲得分類結果。

在參數、損失函數、優化器以及學習率選擇完畢后，就可以進行迭代了。模型的參數會隨著不斷迭代而改變，直至迭代完畢。本實驗的“開始迭代”組件中提供了如下圖所示的迭代次數：

4.1.4 更新模型參數并顯示

選擇好迭代次數后，就需要設置一個顯示頻率，用來觀察迭代過程中參數和損失值的變化，如下圖所示：

接著就是觀察迭代過程中參數和損失值的變化，通過“決策邊界繪制與輸出”組件即可觀察，其內容如下：

4.1.5?pytroch 實現 sigmoid +二元交叉熵代碼?

# 導入包
# pytroch 實現  sigmoid +二元交叉熵
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optimizer
import matplotlib.pyplot as plt
# 設置一下隨機數種子確保每一次運行結果一致
seed=42
torch.manual_seed(seed)
# 1散點輸入
class1_points = np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])
class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])
# 不用單獨提取x1_data 和x2_data
# 框架會根據輸入特征自動提取
# 2.獲得訓練數據和標簽
x_train = np.concatenate((class1_points, class2_points), axis=0)
y_train = np.concatenate((np.zeros(len(class1_points)), np.ones(len(class2_points))))
#3.轉化成張量
x_train_tensor=torch.tensor(x_train,dtype=torch.float32)
y_train_tensor=torch.tensor(y_train,dtype=torch.float32)
#4.定義前向傳播模型
class LogisticRegreModel(nn.Module):#__init__def __init__(self):#繼承父類super(LogisticRegreModel, self).__init__()#自定義層self.fc=nn.Linear(2,1)#forward 層def forward(self,x):x = self.fc(x)#使用激活函數， 獲得sigmoid 之后的tensor值x=torch.sigmoid(x)return x
# 網絡模型初始化 申請個對象 實例化網絡對象
model = LogisticRegreModel()
# 5.定義損失函數和優化器
# 定義損失函數 使用二元交叉熵
cri=nn.BCELoss()
# 需要輸入模型參數和學習率
lr = 0.05
optimizer = optimizer.SGD(model.parameters(), lr=lr)# 最后畫圖
fig, (ax1, ax2) = plt.subplots(1, 2)
# 獲得右邊的損失和迭代次數
epoch_list = []
epoch_loss = []
# 最后畫圖
# 7.迭代訓練
epochs = 1000
for epoch in range(1, epochs + 1):# 前向傳播進行預測y_pre = model(x_train_tensor)# 損失函數將預測結果和真實結果計算損失loss = cri(y_pre, y_train_tensor.unsqueeze(1))# 反向傳播與優化# 1.第一步清空梯度optimizer.zero_grad()# 2第二步反向傳播計算梯度loss.backward()# 3.參數更新optimizer.step()#展示一下假設你模型訓練好了然后進行實際預測怎么得到貓和狗的類別model.eval()with torch.no_grad():pre=model(torch.tensor([[1.9, 1.2]]))list_class=['貓','狗']#tensor中.detach表示從計算圖分離出一個新的張量#.cpu()表示從gpu上轉到cpu#.item()轉為數值max_loc=int(np.round(pre.detach().cpu().item()))print(list_class[max_loc])if epoch % 50 == 0 or epoch == 1:print(f"epoch:{epoch},loss:{loss}")# 畫左圖# 從模型獲得w1和w2 及b的參數w1, w2 = model.fc.weight.data[0]b = model.fc.bias.data[0]# w1*x1+w2*x2+b=0# 求出斜率和截距if w2 != 0:slope = -w1 / w2intercept = -b / w2# 繪制直線 開始結束位置x_min, x_max = 0, 5x = np.array([x_min, x_max])y = slope * x + interceptax1.clear()ax1.plot(x, y, 'r')# 畫散點圖ax1.scatter(x_train[:len(class1_points), 0], x_train[:len(class1_points), 1])ax1.scatter(x_train[len(class1_points):, 0], x_train[len(class1_points):, 1])# 畫右圖ax2.clear()epoch_list.append(epoch)epoch_loss.append(loss.item())ax2.plot(epoch_list, epoch_loss, 'b')plt.pause(1)

4.1.6 softmax+多元交叉熵代碼

# 導入包
# pytroch 實現  sigmoid +二元交叉熵
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optimizer
import matplotlib.pyplot as plt
# 設置一下隨機數種子確保每一次運行結果一致
seed=42
torch.manual_seed(seed)
# 1散點輸入
class1_points = np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])
class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])
# 不用單獨提取x1_data 和x2_data
# 框架會根據輸入特征自動提取
# 2.獲得訓練數據和標簽
x_train = np.concatenate((class1_points, class2_points), axis=0)
y_train = np.concatenate((np.zeros(len(class1_points)), np.ones(len(class2_points))))
#3.轉化成張量
x_train_tensor=torch.tensor(x_train,dtype=torch.float32)
#因為softmax需要轉化成onehot編碼所以類型是torch.long
y_train_tensor=torch.tensor(y_train,dtype=torch.long)
#4.定義前向傳播模型
class LogisticRegreModel(nn.Module):#__init__def __init__(self):#繼承父類super(LogisticRegreModel, self).__init__()#自定義層 #修改成輸出為2類self.fc=nn.Linear(2,2)#forward 層def forward(self,x):x = self.fc(x)return x
# 網絡模型初始化 申請個對象 實例化網絡對象
model = LogisticRegreModel()
# 5.定義損失函數和優化器
# 定義損失函數 使用多元交叉熵 里面包括softmax
cri=nn.CrossEntropyLoss()
# 需要輸入模型參數和學習率
lr = 0.05
optimizer = optimizer.SGD(model.parameters(), lr=lr)# 最后畫圖
fig, (ax1, ax2) = plt.subplots(1, 2)
# 獲得右邊的損失和迭代次數
epoch_list = []
epoch_loss = []
# 最后畫圖
# 7.迭代訓練
epochs = 1000
for epoch in range(1, epochs + 1):# 前向傳播進行預測y_pre = model(x_train_tensor)# 損失函數將預測結果和真實結果計算損失#y_train_tensor不需要擴維度，因為交叉熵會自動轉換成onehot編碼loss = cri(y_pre, y_train_tensor)# 反向傳播與優化# 1.第一步清空梯度optimizer.zero_grad()# 2第二步反向傳播計算梯度loss.backward()# 3.參數更新optimizer.step()#展示一下假設你模型訓練好了然后進行實際預測怎么得到貓和狗的類別model.eval()with torch.no_grad():#模型輸出后需要softmax轉化成概率值pre=torch.softmax(model(torch.tensor([[1.9, 1.2]])),dim=1)list_class=['貓','狗']#tensor中.detach表示從計算圖分離出一個新的張量#.cpu()表示從gpu上轉到cpu#.numpy()轉為數值max_loc=np.argmax(pre.detach().cpu().numpy())print(list_class[max_loc])if epoch % 50 == 0 or epoch == 1:print(f"epoch:{epoch},loss:{loss}")# 畫左圖# 從模型獲得w1和w2 及b的參數w1, w2 = model.fc.weight.data[0]b = model.fc.bias.data[0]# w1*x1+w2*x2+b=0# 求出斜率和截距if w2 != 0:slope = -w1 / w2intercept = -b / w2# 繪制直線 開始結束位置x_min, x_max = 0, 5x = np.array([x_min, x_max])y = slope * x + interceptax1.clear()ax1.plot(x, y, 'r')# 畫散點圖ax1.scatter(x_train[:len(class1_points), 0], x_train[:len(class1_points), 1])ax1.scatter(x_train[len(class1_points):, 0], x_train[len(class1_points):, 1])# 畫右圖ax2.clear()epoch_list.append(epoch)epoch_loss.append(loss.item())ax2.plot(epoch_list, epoch_loss, 'b')ax2.set_xlabel('epoch')ax2.set_ylabel('loss')plt.pause(1)

總結

????????文章圍繞邏輯回歸的核心數學原理展開，首先通過取對數將連乘運算轉化為連加形式，簡化計算；隨后深入分析交叉熵及其在分類任務中的應用，揭示其與負對數似然函數的等價性，并擴展至多分類場景。核心部分以二分類問題為案例，結合Sigmoid函數、梯度下降等工具實現邏輯回歸模型，同時對比二元交叉熵與Softmax多分類交叉熵的差異。最后通過PyTorch框架代碼實現兩類任務的訓練過程，動態展示參數更新與損失變化，幫助讀者理解理論到實踐的完整鏈路。