13回溯
一、回溯1
例題1–遞歸實現排列型枚舉-藍橋19684
1.遞歸可以解決不定次數的循環問題
2.使用數組來標記數字是否被選過

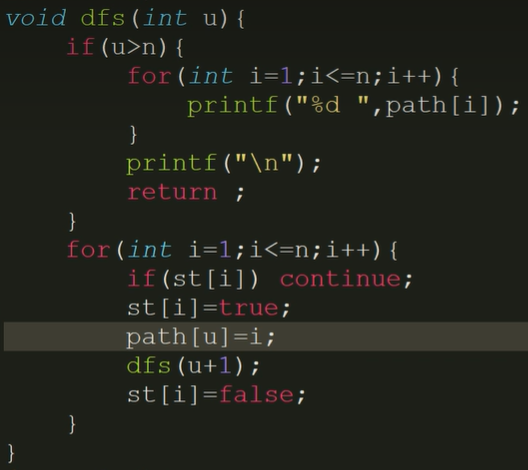
import java.util.Scanner;public class Main {static int n;static boolean[] st = new boolean[10]; //判斷數字是否被選過static int[] path = new int[10]; //存儲排列組合//遞歸程序public static void dfs(int u){if(u > n){//遞歸結束的條件,遞歸結束就輸出結果。(但這里其實是針對每一次的排序而言)for (int i = 1; i <= n; i++) {System.out.print(path[i] + " ");}System.out.println();return;}//遞歸--循環排列組合for (int i = 1; i <= n ; i++) {if(st[i]) continue;st[i] = true;//選中path[u] = i; //記錄dfs(u + 1); //下一個數的循環st[i] = false; //解除}}public static void main(String[] args) {Scanner sc = new Scanner(System.in);n = sc.nextInt();dfs(1);
/* for (int i = 1; i <= n ; i++) {st[i] = true;for (int j = 1; j <= n ; j++) {
// if(j == i) continue;if(st[j]) continue;st[j] = true;for (int k = 1; k <= n ; k++) {
// if (k == i || k ==j) continue;if(st[k]) continue;System.out.println(i+ "," + j + "," + k);}st[j] = false;}st[i] = false;}*/}
}
*特別注意!!!
結果對但是沒有通過用例,原因是輸出的格式問題!各個數之間要用空格隔開!這點特別需要注意。
例題2–串變換藍橋4360
對k個操作進行全排列。以及k--的排列,直到可以變為T串,或循環到最后都變不了
例題3–帶分數藍橋208
回溯+枚舉
思路,1-9出現且只出現1次,進行9的全排列,把9個數的所有組合排列出來,再把加號和除號放進去,看看哪些符合條件
import java.util.*;public class Main {static int N;static int count = 0;//static List<String> permutations = new ArrayList<>();public static void main(String[] args) {Scanner sc = new Scanner(System.in);N = sc.nextInt();sc.close();// 生成1~9的所有排列permute("123456789", 0, 8);System.out.println(count);}// 生成全排列public static void permute(String str, int l, int r) {if (l == r) {//permutations.add(str);check(str);} else {for (int i = l; i <= r; i++) {str = swap(str, l, i);permute(str, l + 1, r);str = swap(str, l, i); // 回溯}}}// 檢查所有的加號和除號位置public static void check(String str) {for (int i = 1; i <= 7; i++) { // 加號位置,要大于0for (int j = i + 1; j <= 8; j++) { // 除號位置,在加號的右邊int A = Integer.parseInt(str.substring(0, i));int B = Integer.parseInt(str.substring(i, j));int C = Integer.parseInt(str.substring(j));// 避免除0錯誤if (C == 0) continue;// 判斷是否符合 A + B / C = Nif (A + (double) B / C == N) {count++;}}}}// 字符串交換工具方法public static String swap(String str, int i, int j) {char[] charArray = str.toCharArray();char temp = charArray[i];charArray[i] = charArray[j];charArray[j] = temp;return new String(charArray);}
}1234
1243
1324
1342
1432
1423
2134
2143
2314
2341
2431
2413
3214
3241
3124
3142
3412
3421
4231
4213
4321
4312
4132
4123
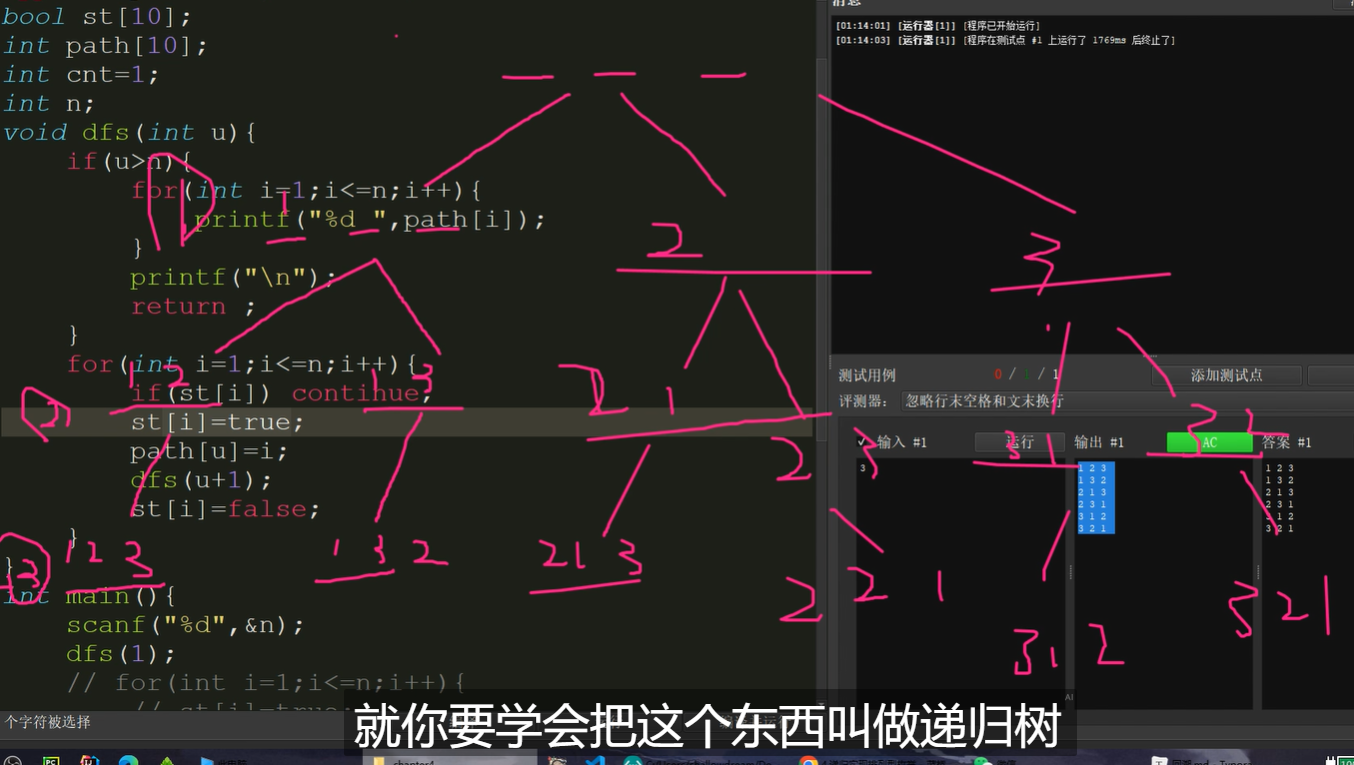
理解回溯中的關鍵操作
str = swap(str, l, i);
- 做選擇:交換當前元素和
i位置的元素,相當于嘗試將i放在當前的位置。
permute(str, l + 1, r);
- 遞歸調用:繼續處理后面的數字,進入下一層。
str = swap(str, l, i);
- 撤銷選擇:把字符串恢復到原來的狀態,確保不影響下一次的嘗試。
- 這是 回溯的精髓:探索完一條路徑后,將狀態恢復,以便繼續探索其他路徑。
建議:用樹狀圖畫出回溯的執行過程,一步步理解狀態的變化。
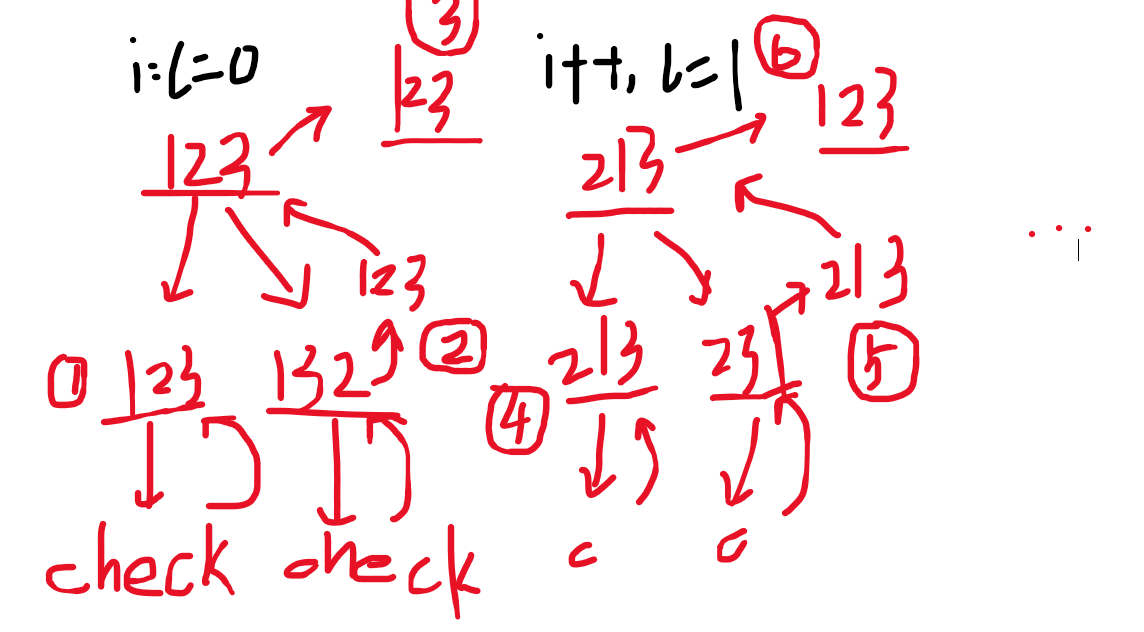
幾道回溯小題
二、回溯2
例題–N皇后問題藍橋1508
題目要求也不允許處在與棋盤邊框成 45 角的斜線上。(注意與棋盤邊框)
主對角線
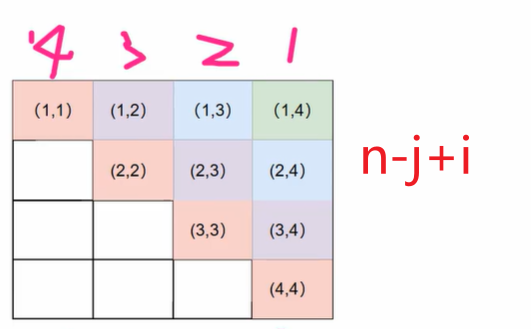
副對角線
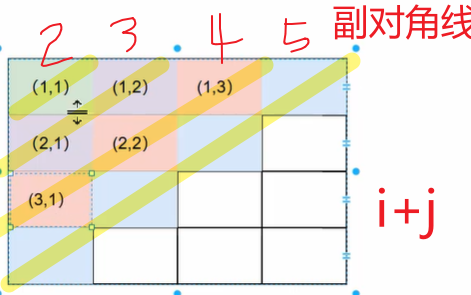
暴力做法
假設n=4,進行4次循環的嵌套,每一次代表的是每一行棋子的位置。
public class Main {static int N = 30;//行row,列col,主對角線zhu,副對角線fustatic boolean[] row = new boolean[N];static boolean[] col = new boolean[N];static boolean[] zhu = new boolean[N];static boolean[] fu = new boolean[N];public static void main(String[] args){int ans = 0;//記錄//一個for表示一行for (int i = 1; i <= N; i++) {//嘗試第1個棋子int x1 = 1,y1 = i;//行//列//被選中了就為truerow[x1] = true;col[y1] = true;zhu[N - y1 + x1] = true;fu[x1 + y1] = true;for (int j = 1; j <= N; j++) {//嘗試第2個棋子int x2 = 2,y2 = j;//行//列//不符合規則的就跳過if(row[x2] || col[y2] || zhu[N - y2 + x2] || fu[x2 + y2]) continue;//被選中了就為truerow[x2] = true;col[y2] = true;zhu[N - y2 + x2] = true;fu[x2 + y2] = true;for (int k = 1; k <= N; k++) {//嘗試第3個棋子//同樣for (int l = 1; l <= N; l++) {//嘗試第4個棋子//同樣,順便ans加加}}//結束要釋放//回溯row[x2] = false;col[y2] = false;zhu[N - y2 + x2] = false;fu[x2 + y2] = false;}//結束要釋放//回溯row[x1] = false;col[y1] = false;zhu[N - y1 + x1] = false;fu[x1 + y1] = false;}}
}
其實上面的row數組是沒必要的,因為循環的就是行數,按行數來的。
dfs遞歸做法
import java.util.Scanner;//TIP To <b>Run</b> code, press <shortcut actionId="Run"/> or
// click the <icon src="AllIcons.Actions.Execute"/> icon in the gutter.
public class Main {static int ans;static int n;static int N = 30;//行row,列col,主對角線zhu,副對角線fu//static boolean[] row = new boolean[N];static boolean[] col = new boolean[N];static boolean[] zhu = new boolean[N];static boolean[] fu = new boolean[N];//遞歸函數public static void dfs(int u){if(u > n){//循環到最后ans++;return;}for (int i = 1; i <= n; i++) {//這表示每一行循環每一列,因此i表示的是列數,u表示的是行數//首先判斷是否被占用if(col[i] || zhu[n - i + u] || fu[u + i]) continue;//選中一個數col[i] = true;zhu[n - i + u] = true;fu[u + i] = true;//遞歸下一行dfs(u + 1);//回溯col[i] = false;zhu[n - i + u] = false;fu[u + i] = false;}}//主邏輯函數public static void solve(){//輸入NScanner sc = new Scanner(System.in);n = sc.nextInt();//調用dfs(1);System.out.println(ans);}public static void main(String[] args) {solve();}
}
學到的知識點:
1.難點:本題要求不能在同一行,同一列和與棋盤邊框成45度角。
45度角這個需要找規律。
把這些情況都轉換為設為一個布爾數組,來判斷是否被放置。true--被放置,false--沒有。
2.學習到的遞歸知識:
首先,設n為4,進行一個暴力的做法。
就是遍歷每一行,對于每一行,判斷某個位置是否符合條件(1中的條件)。
符合條件后,設定其被放置,進行下一層遍歷。否則continue。
對于一次找到合法的放置位置后,需要將位置進行釋放--這就是回溯。因此,將暴力的做法轉為遞歸,就容易了。
找到一個合法的放置位置(u>x后),ans++;
遞歸函數中,為每一行的遍歷。
一行遍歷完后進行下一行的遞歸(dfs(u + 1));
下面幾行回溯。
寫完代碼看完視頻又忘記思路,不好說。只可意會。
三、回溯3-子集枚舉(遞歸實現指數型枚舉)
一旦涉及選與不選,刪和不刪,留和不留-->兩種狀態-->就要想到子集枚舉
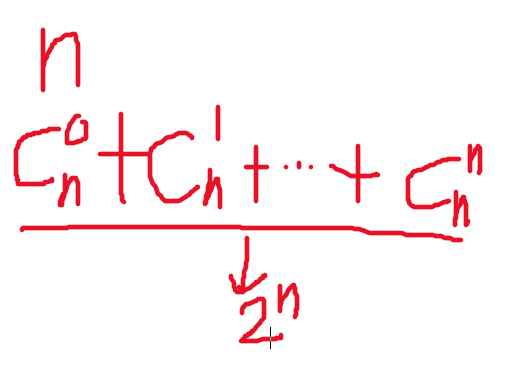
例題1–遞歸實現指數型枚舉19685

其實看不懂這個題目,好奇怪的題目。根據老師的解析來寫。
大致理解為從1-n中,輸出所有的組合數就對了。
我知道了,就是要按照題目的要求來,要先判斷0不選,再判斷1選。具體看代碼更了解。
暴力做法
假設n=3.
public class Main {static int[] st = new int[10];//主邏輯函數public static void solve(){int n = 3;for (int i = 0; i <=1; i++) {//表示選或不選st[1] = i;for (int j = 0; j <= 1; j++) {//表示選或不選st[2] = j;for (int k = 0; k <= 1; k++) {//表示選或不選st[3] = k;for (int l = 1; l <= 3; l++) {//選中的輸出if(st[l] == 1) System.out.print(l);}System.out.println();}}}}public static void main(String[] args) {solve();}
}
使用回溯dfs來實現
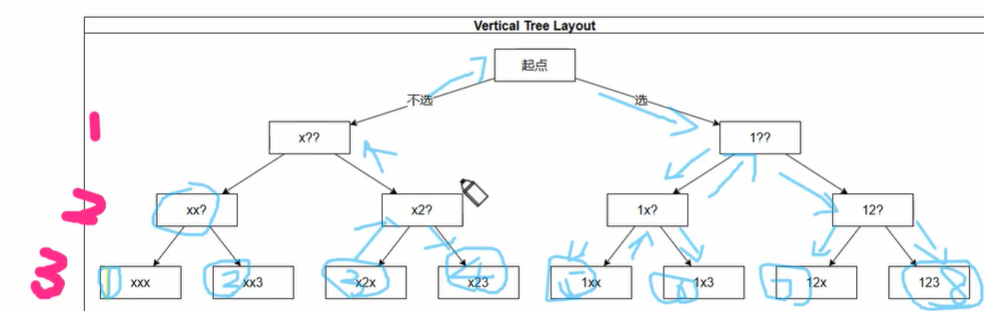
import java.util.Scanner;//TIP To <b>Run</b> code, press <shortcut actionId="Run"/> or
// click the <icon src="AllIcons.Actions.Execute"/> icon in the gutter.
public class Main {static int n;static int[] st = new int[20];//遞歸函數public static void dfs(int u){if(u > n){//一次結束,輸出結果for (int l = 1; l <= n; l++) {//選中的輸出if(st[l] == 1) System.out.print(l + " ");}System.out.println();return;//這里要返回,因為?}for (int i = 0; i <= 1; i++) {st[u] = i;dfs(u + 1);//下一個數選或不選}}//主邏輯函數public static void solve(){Scanner sc = new Scanner(System.in);n = sc.nextInt();dfs(1);
// for (int i = 0; i <=1; i++) {//表示選或不選
// st[1] = i;
// for (int j = 0; j <= 1; j++) {//表示選或不選
// st[2] = j;
// for (int k = 0; k <= 1; k++) {//表示選或不選
// st[3] = k;
// for (int l = 1; l <= 3; l++) {
// //選中的輸出
// if(st[l] == 1) System.out.print(l);
// }
// System.out.println();
// }
// }
// }}public static void main(String[] args) {solve();}
}
特別注意輸出的格式問題,空格或者逗號特別注意,總因為這個沒通過!!!
例題2–19880
例題3–蛋糕的美味值8664
package huisu;import java.util.Scanner;public class TasteCake {static int[] cake = new int[30];static int[] st = new int[30];static int n,k;static int max;//獲得最大的總和public static void getMax(){int sum = 0;for (int i = 1; i <= n; i++) {if(st[i] == 1){//被選中并且美味值小于ksum += cake[i];}}//結束后返回目前最大值if(sum < k){max = Math.max(sum,max);}}//遞歸public static void dfs(int u){//u表示第幾個蛋糕if(u > n){//表示n個蛋糕選與不選完了getMax();return;}for (int i = 0; i <= 1; i++) {//選與不選st[u] = i;dfs(u + 1);//下一個蛋糕}}//主邏輯函數public static void solve(){Scanner sc = new Scanner(System.in);//輸入n,kn = sc.nextInt();k = sc.nextInt();//輸入蛋糕的美味值for (int i = 1; i <= n; i++) {cake[i] = sc.nextInt();}//遞歸dfs(1);//輸出結果System.out.println(max);}public static void main(String[] args) {solve();}
}注意:
一定要看清題目啊,看題目和觀察樣例。
這里是要選出的蛋糕的總值小于k,而不是選出的每一個小于k的。
我第一次寫理解為后面那一種,就錯了。
其實看樣例也能看出來。
題目真難理解。。。
例題4–luoguP1036
思想
老師說只需要思考最后兩層的遞歸,其他層的遞歸其實就和最后兩層一樣
對于選與不選的遞歸問題,事件復雜度都是2^n,對于n<=25的都可以運行











![[RH342]iscsi配置與排錯](http://pic.xiahunao.cn/[RH342]iscsi配置與排錯)
(文末有下載方式))
)





紐約出租車大數據分析實戰:從Hadoop到Azkaban的全鏈路解析與優化)