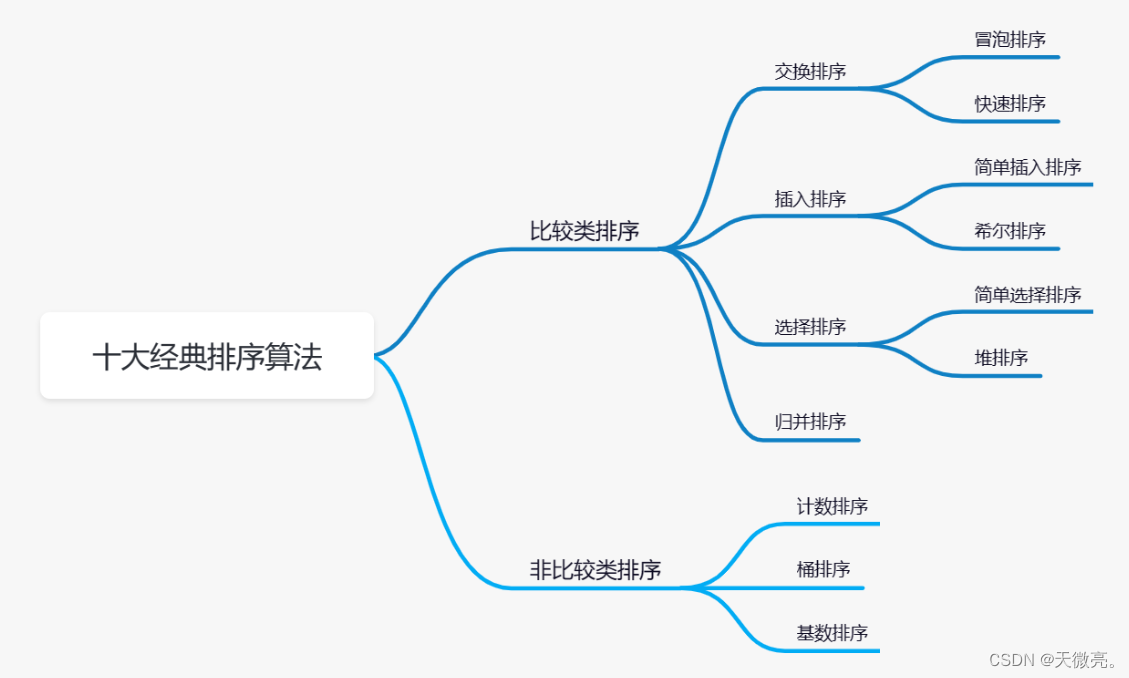
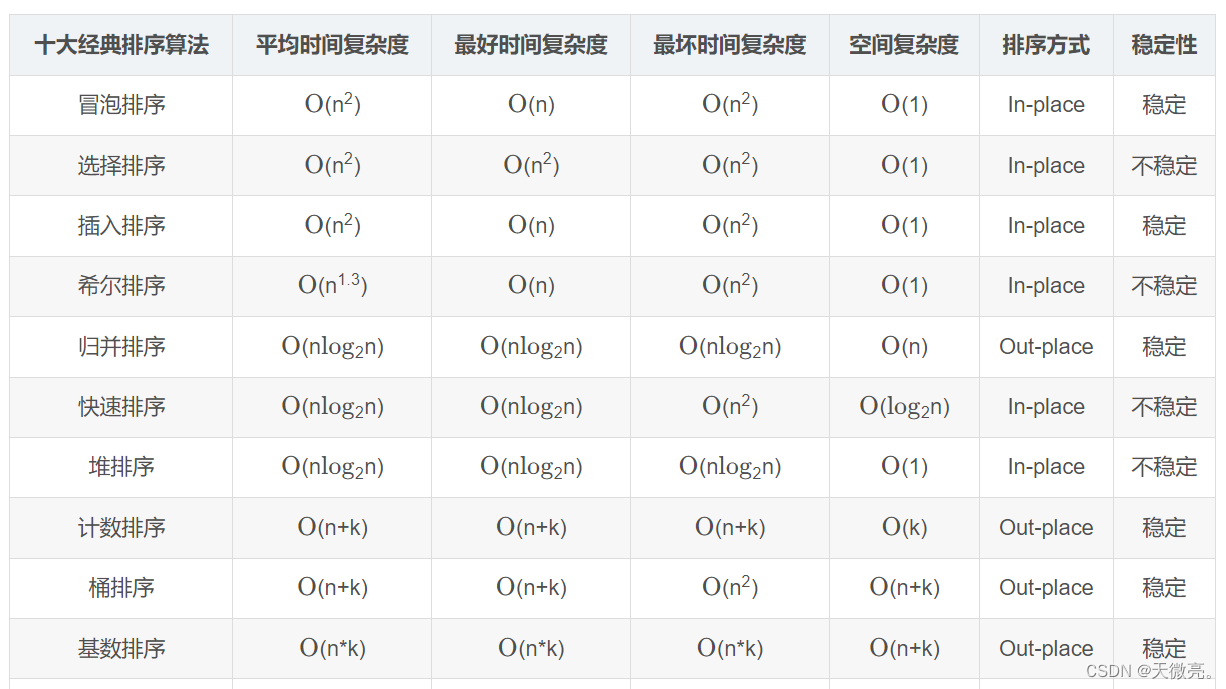
參考： 排序算法總結

冒泡排序（穩定）

經過多次迭代，通過相鄰元素之間的比較與交換，使值較小的元素逐步從后面移到前面，值較大的元素從前面移到后面。

這個過程就像水底的氣泡一樣從底部向上「冒泡」到水面，這也是冒泡排序法名字的由來。

接下來，我們使用「冒泡」的方式來模擬一下這個過程。

首先將數組想象是一排「泡泡」，元素值的大小與泡泡的大小成正比。
然后從左到右依次比較相鄰的兩個「泡泡」：
如果左側泡泡大于右側泡泡，則交換兩個泡泡的位置。
如果左側泡泡小于等于右側泡泡，則兩個泡泡保持不變。

這趟遍歷完成之后，最大的泡泡就會放置到所有泡泡的最右側，就像是「泡泡」從水底向上浮到了水面。

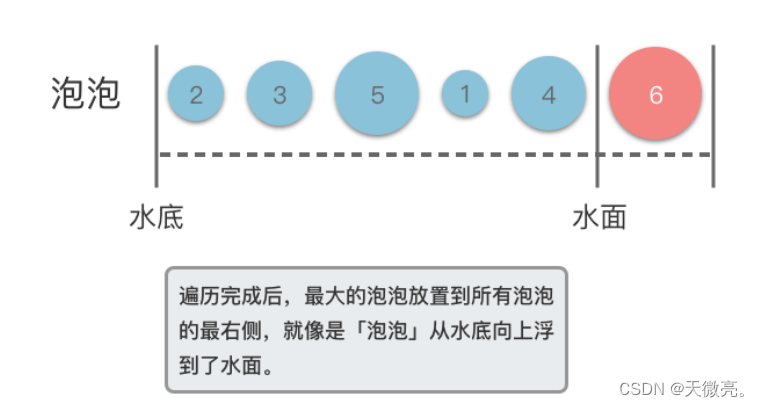
public class BubbleSort {public static void bubbleSort(int[] arr) {int len = arr.length;for (int i = 0; i < len - 1; i++) {boolean flag = true;for (int j = 0; j < len - i - 1; j++) {if (arr[j] > arr[j + 1]) {int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;flag = false;}}if (flag) {break;}}}
}

選擇排序（不穩定）

將數組分為兩個區間：左側為已排序區間，右側為未排序區間。每趟從未排序區間中選擇一個值最小的元素，放到已排序區間的末尾，從而將該元素劃分到已排序區間。

算法步驟

1. 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置；
2. 再從剩余未排序元素中繼續尋找最小（大）元素，然后放到已排序序列的末尾；
3. 重復第2步，直到所有元素均排序完畢。
   

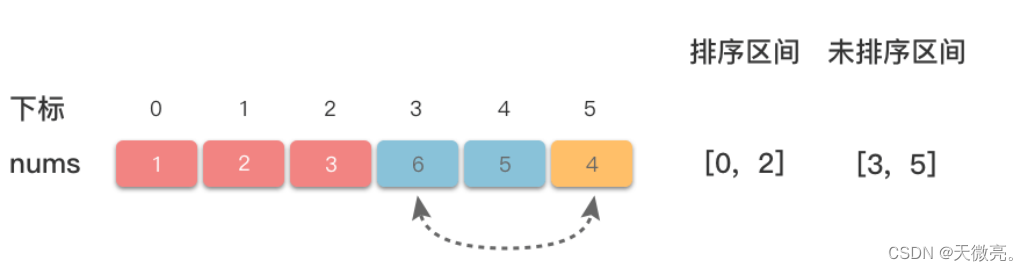
public class SelectionSort {public static void selectionSort(int[] arr) {int len = arr.length;for (int i = 0; i < len - 1; i++) {int minVal = i;for (int j = i + 1; j < len; j++) {if (arr[minVal] > arr[j]) {minVal = j;}}if (minVal != i) {int tmp = arr[i];arr[i] = arr[minVal];arr[minVal] = tmp;}}}
}

插入排序（穩定）

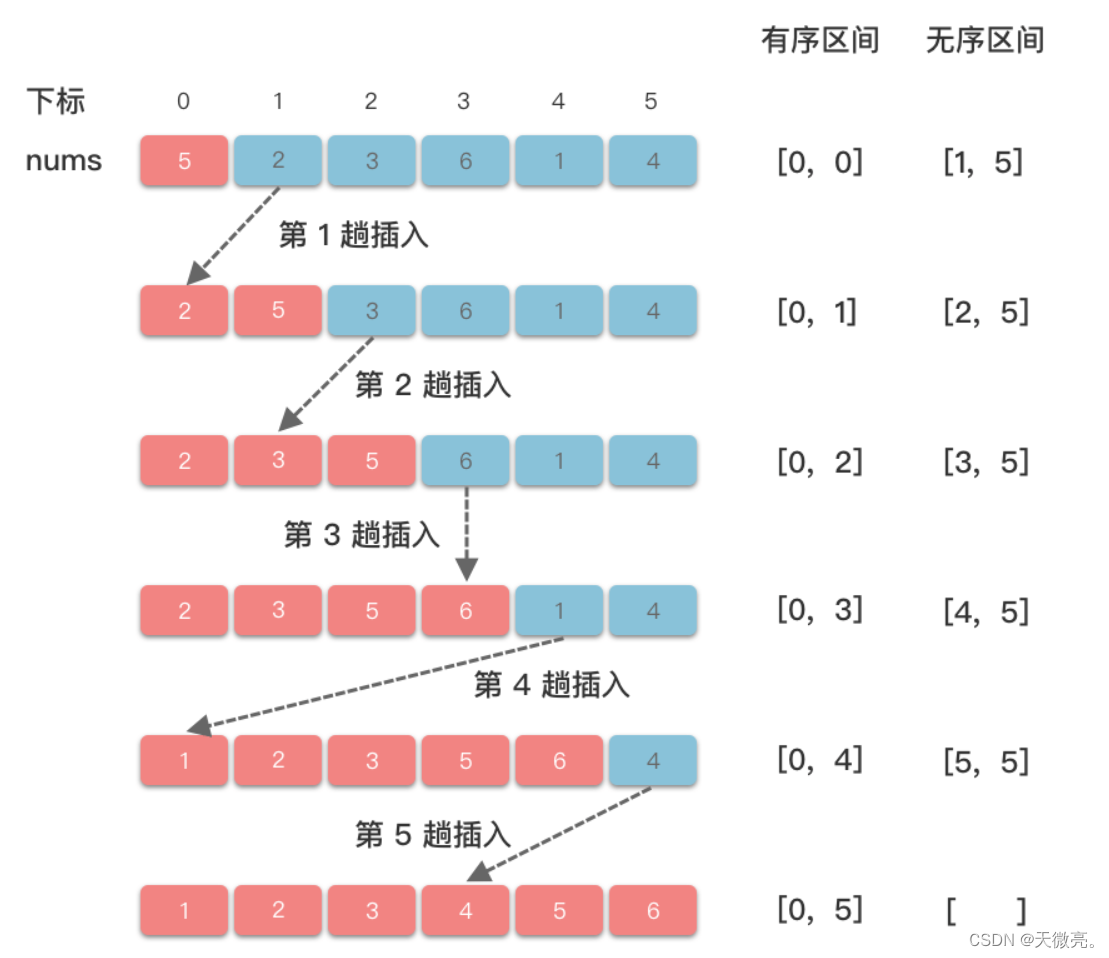
將數組分為兩個區間：左側為有序區間，右側為無序區間。每趟從無序區間取出一個元素，然后將其插入到有序區間的適當位置。

算法步驟

1. 首先從第一個元素開始，該元素被認為是有序的；
2. 取出下一個元素，在已經排序的元素序列中從后往前進行掃描；
3. 如果該已排好序的元素大于新元素，則將該元素移到下一位置；
4. 重復步驟3一直往前進行掃描比較，直到找到已排序的元素小于或者等于新元素的位置；
5. 將新元素插入到該位置后；
6. 重復步驟2~5。
   

public class InsertionSort {public static void insertionSort(int[] arr) {for (int i = 1; i < arr.length; i++) {int val = arr[i], j = i;while (j > 0 && val < arr[j - 1]) {arr[j] = arr[j - 1];j--;}arr[j] = val;}}
}

希爾排序（不穩定）

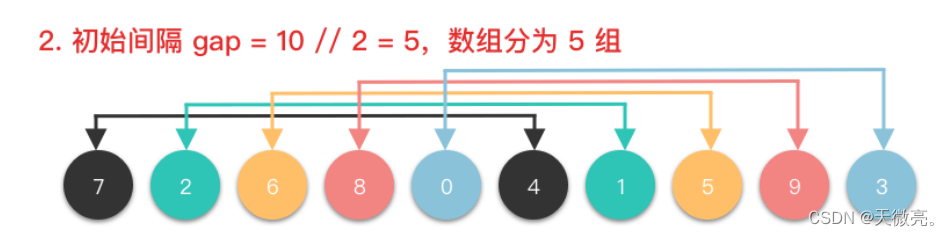
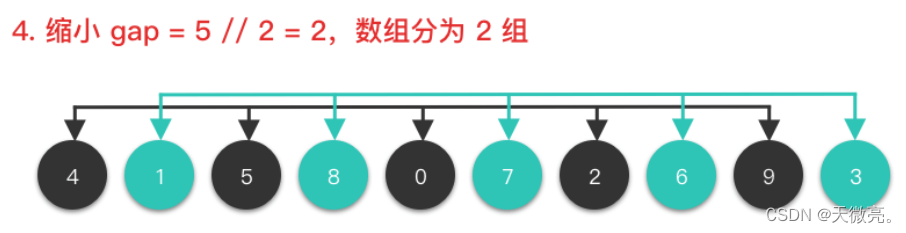
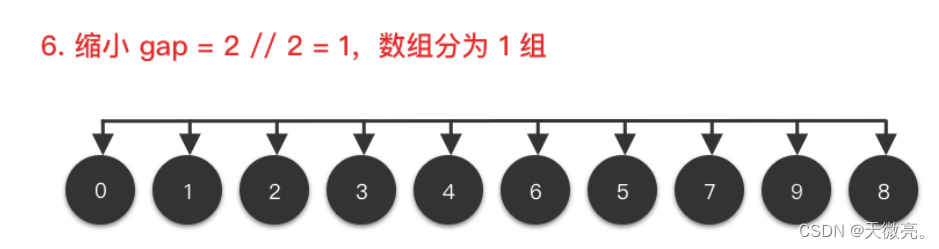
將整個數組切按照一定的間隔取值劃分為若干個子數組，每個子數組分別進行插入排序。然后逐漸縮小間隔進行下一輪劃分子數組和對子數組進行插入排序。直至最后一輪排序間隔為1，對整個數組進行插入排序。

算法步驟

1. 選擇一個增量序列{t1, t2, …, tk}；
2. 按增量序列個數k，對序列進行k趟排序；
3. 每趟排序，根據對應的增量t，將待排序列分割成若干長度為m的子序列，分別對各子表進行直接插入排序。僅增量因子為1時，整個序列作為一個表來處理，表長度即為整個序列的長度。
   其中，增量gap=length/2，縮小增量繼續以gap = gap/2的方式，這種增量選擇我們可以用一個序列來表示，{n/2, (n/2)/2, …, 1}，稱為增量序列。一般的增量序列都選擇以上說明的這個，但不一定是最優的。

public class ShellSort {public static void shellSort(int[] arr) {int len = arr.length, tmp, j;for (int gap = len / 2; gap >= 1; gap = gap / 2) {for (int i = gap; i < len; i++) {tmp = arr[i];j = i - gap;while (j >= 0 && arr[j] > tmp) {arr[j + gap] = arr[j];j -= gap;}arr[j + gap] = tmp;}}}
}

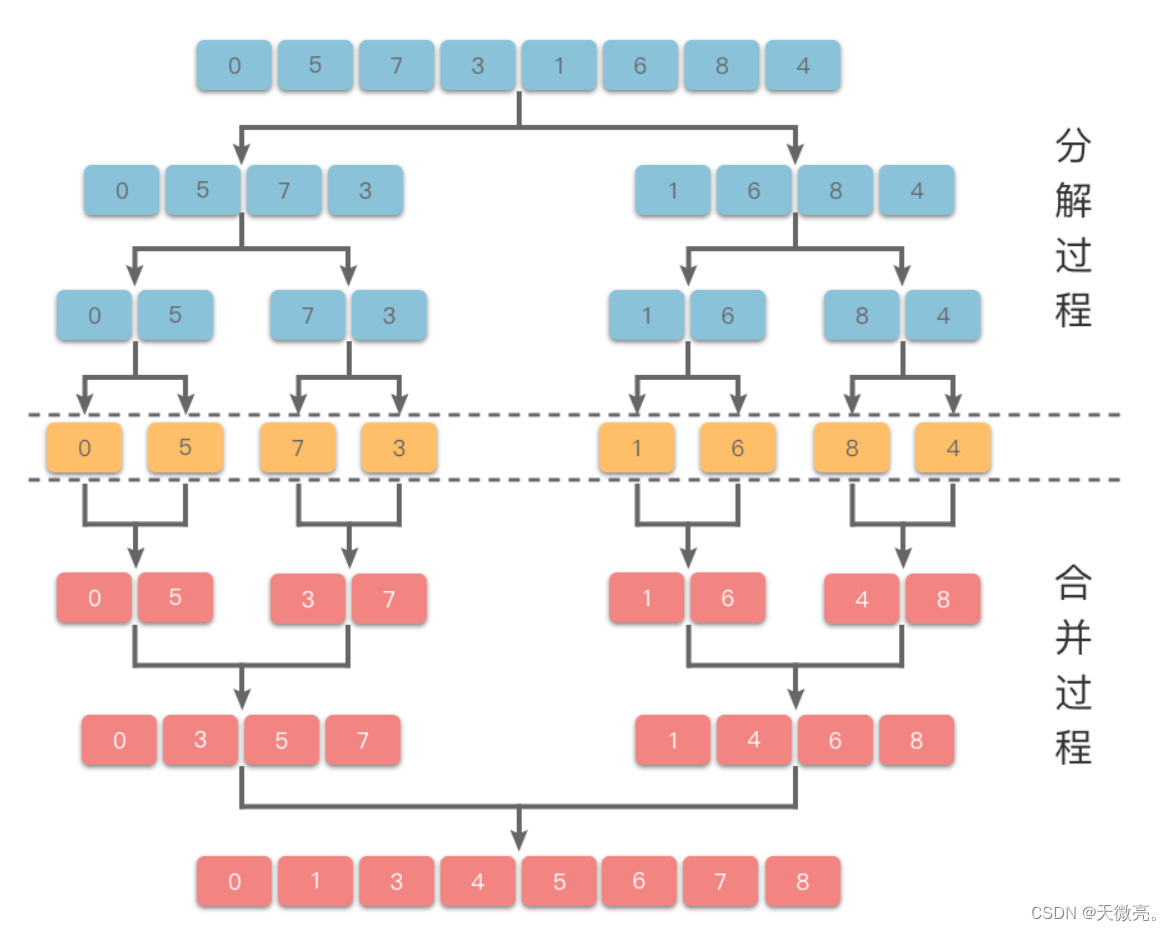
歸并排序（穩定）

采用經典的分治策略，先遞歸地將當前數組平均分成兩半，然后將有序數組兩兩合并，最終合并成一個有序數組。

以下是ACWing版本的java模板

public class MergeSort {// 歸并排序private static void merge_sort(int[] arr, int l, int r) {// 遞歸結束條件if (l >= r) return;// 以下都為邏輯部分int mid = l + ((r - l) >> 1);merge_sort(arr, l, mid);merge_sort(arr, mid + 1, r);int[] tmp = new int[r - l + 1]; // 臨時數組, 用于臨時存儲 [l,r]區間內排好序的數據int i = l, j = mid + 1, k = 0;  // 兩個指針// 進行歸并while (i <= mid && j <= r) {if (arr[i] <= arr[j]) tmp[k++] = arr[i++];elsetmp[k++] = arr[j++];}while (i <= mid) tmp[k++] = arr[i++];while (j <= r) tmp[k++] = arr[j++];// 進行賦值for (i = l, j = 0; i <= r; i++, j++)arr[i] = tmp[j];}
}

快速排序（不穩定）

采用經典的分治策略，選擇數組中某個元素作為樞軸，通過一趟排序將數組分為獨立的兩個子數組，一個子數組中所有元素值都比樞軸小，另一個子數組中所有元素值都比樞軸大。然后再按照同樣的方式遞歸的對兩個子數組分別進行快速排序，以達到整個數組有序。

以下是ACWing版本的java模板

// 快速排序算法模板（選用）public static void quickSort(int[] q,int l,int r){if(l>=r)return;int i = l-1, j = r+1, x = q[l+r>>1]; //2. 因為j不能取到右邊界,所以取下界(q[l]或q[l+r>>1])while(i<j){do i++; while(q[i]<x);do j--; while(q[j]>x);if(i<j){int tmp = q[i];q[i]=q[j];q[j]=tmp;}}quickSort(q,l,j);  //1. j不能取到右邊界，若取到則會無限遞歸下去 此時q[j]<=x，q[j+1]>=x而x是2.中定義的quickSort(q,j+1,r); }

// 快速排序算法模板（其他）public static void quickSort(int[] q,int l,int r){if(l>=r)return;int i = l-1, j = r+1, x = q[l+r+1>>1]; //2. 因為i不能取到左邊界,所以取上界(q[r]或q[l+r+1>>1])while(i<j){do i++; while(q[i]<x);do j--; while(q[j]>x);if(i<j){int tmp = q[i];q[i]=q[j];q[j]=tmp;}}quickSort(q,l,i-1);  quickSort(q,i,r); //1. i不能取到左邊界，若取到則會無限遞歸下去 此時q[i-1]<=x，q[i]>=x，而x是2.中定義的}

堆排序

計數排序

桶排序

基數排序

二分查找

二分查找算法（Binary Search Algorithm）：也叫做折半查找算法、對數查找算法，是一種用于在有序數組中查找特定元素的高效搜索算法。

二分查找的基本算法思想為：通過確定目標元素所在的區間范圍，反復將查找范圍減半，直到找到元素或找不到該元素為止。

整數二分法模板(ACWing版)
二分的本質是邊界
二分法用于查找, 每次都選擇答案所在的區間再次進行查找, 當區間長度為 1時, 就是答案

// 模板一
// 區間[l, r]被劃分成 [l, mid] 和 [mid+1, r]時使用
int bsearch_1(int l, int r) {while (l < r) {int mid = l + r >> 1;if (check[mid)  // check() 判斷 mid是否滿足性質r = mid; elsel = mid + 1;}return l;
}

// 模板二
// 區間[l, r]被劃分成 [l, mid-1] 和 [mid, r]時使用
int bsearch_2(int l, int r) {while (l < r) {int mid = l + r + 1 >> 1;   // 注意if (check[mid)  // check() 判斷 mid是否滿足性質l = mid;elser = mid - 1;}return l;
}
/* 如何選擇模板：
根據 check(mid)來判斷 r和 l的取值范圍
根據取值范圍選擇 mid是否有 + 1操作
mid歸于左邊, r = mid, mid選擇 不 +1
mid歸于右邊, l = mid, mid選擇 +1 */