算法復雜度


-
O(n):表示算法的漸進上界。如果一個算法的運行時間是O(n),那么它的運行時間最多與輸入規模n成正比。換句話說,當輸入規模n增加時,算法的運行時間不會超過某個常數倍的n。比如,如果一個算法的時間復雜度是O(n),那么它的運行時間可能是3n,5n,100n等。
-
Ω(n):表示算法的漸進下界。如果一個算法的運行時間是Ω(n),那么它的運行時間至少與輸入規模n成正比。換句話說,當輸入規模n增加時,算法的運行時間不會比某個常數倍的n小。比如,如果一個算法的時間復雜度是Ω(n),那么它的運行時間可能是n,2n,100n等。
-
Θ(n):表示算法的緊密界限。如果一個算法的運行時間是Θ(n),那么它的運行時間與輸入規模n成正比,并且上界和下界是相同的。換句話說,當輸入規模n增加時,算法的運行時間將以線性方式增長。比如,如果一個算法的時間復雜度是Θ(n),那么它的運行時間可能是3n,n,100n等,但是不會超過某個常數倍的n。
單純判斷算式
?e.g1
e.g2
e.g3
e.g4

?C, 應該是O(n^2)

e.g5

A
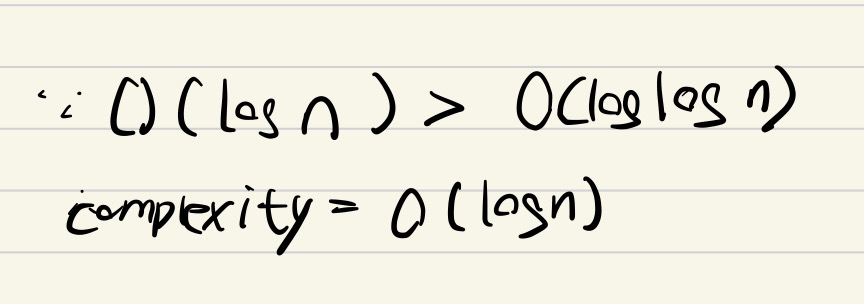
?一般的算法復雜度
e.g1
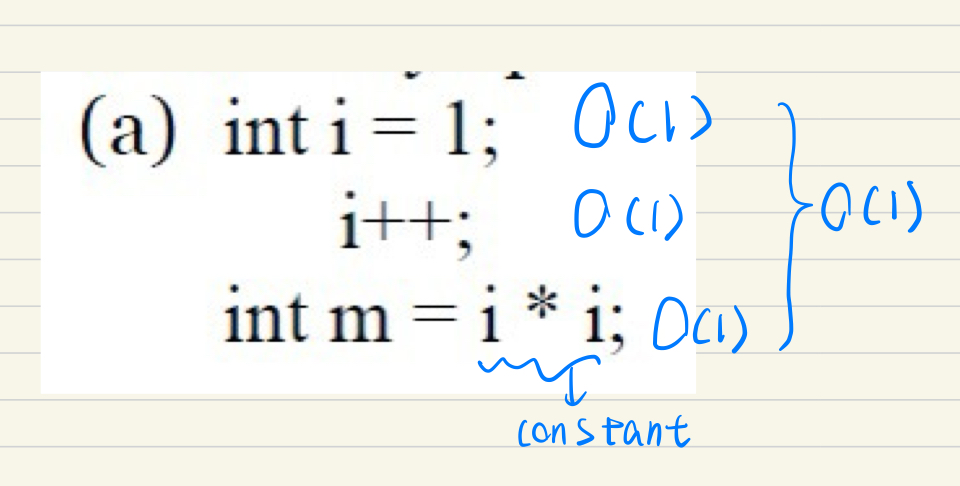

*

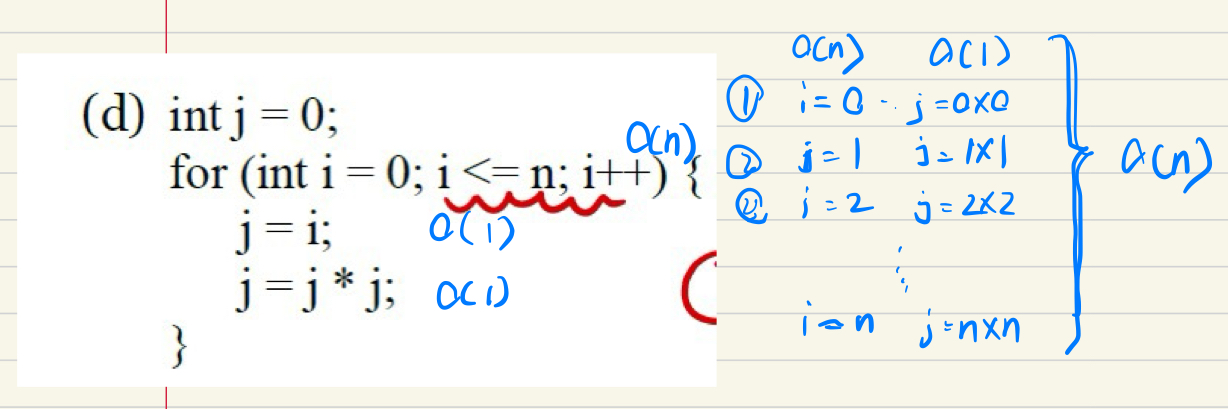

e.g2*

是這樣的,用n^2進行遍歷,然后n進行計算,乘起來就是n^3
e.g3


e.g4*

注意第二題,log(a)+log(b) = log(ab) 我反正忘了哈哈哈哈哈
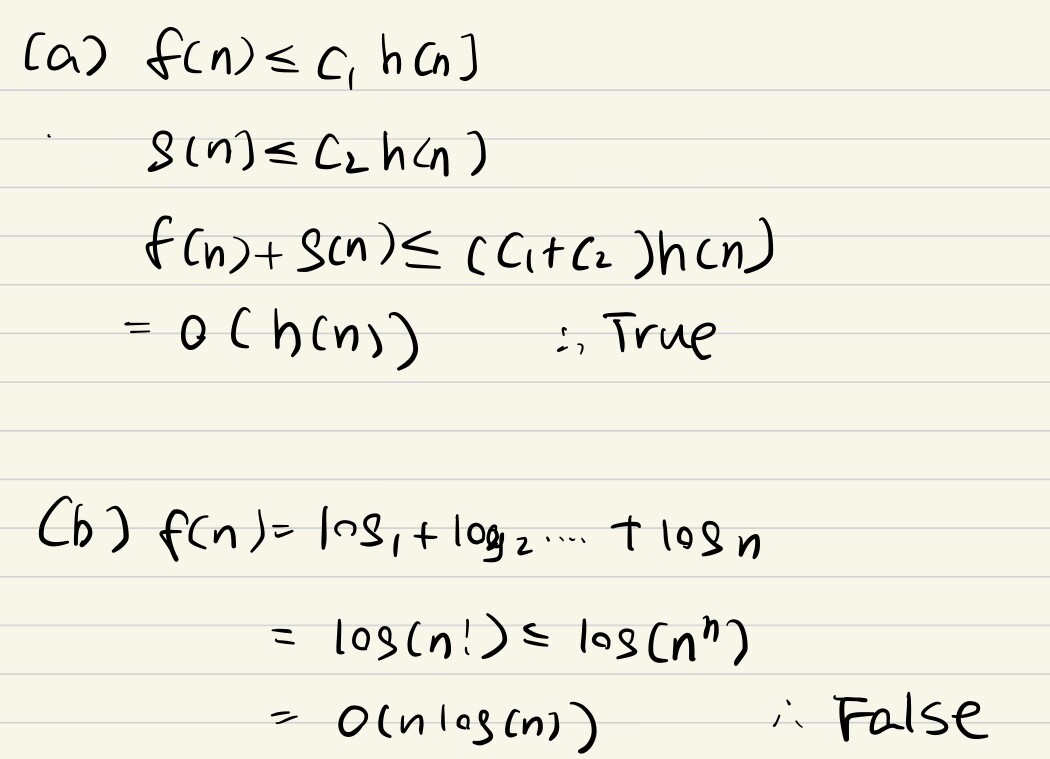
e.g5 summation表達*

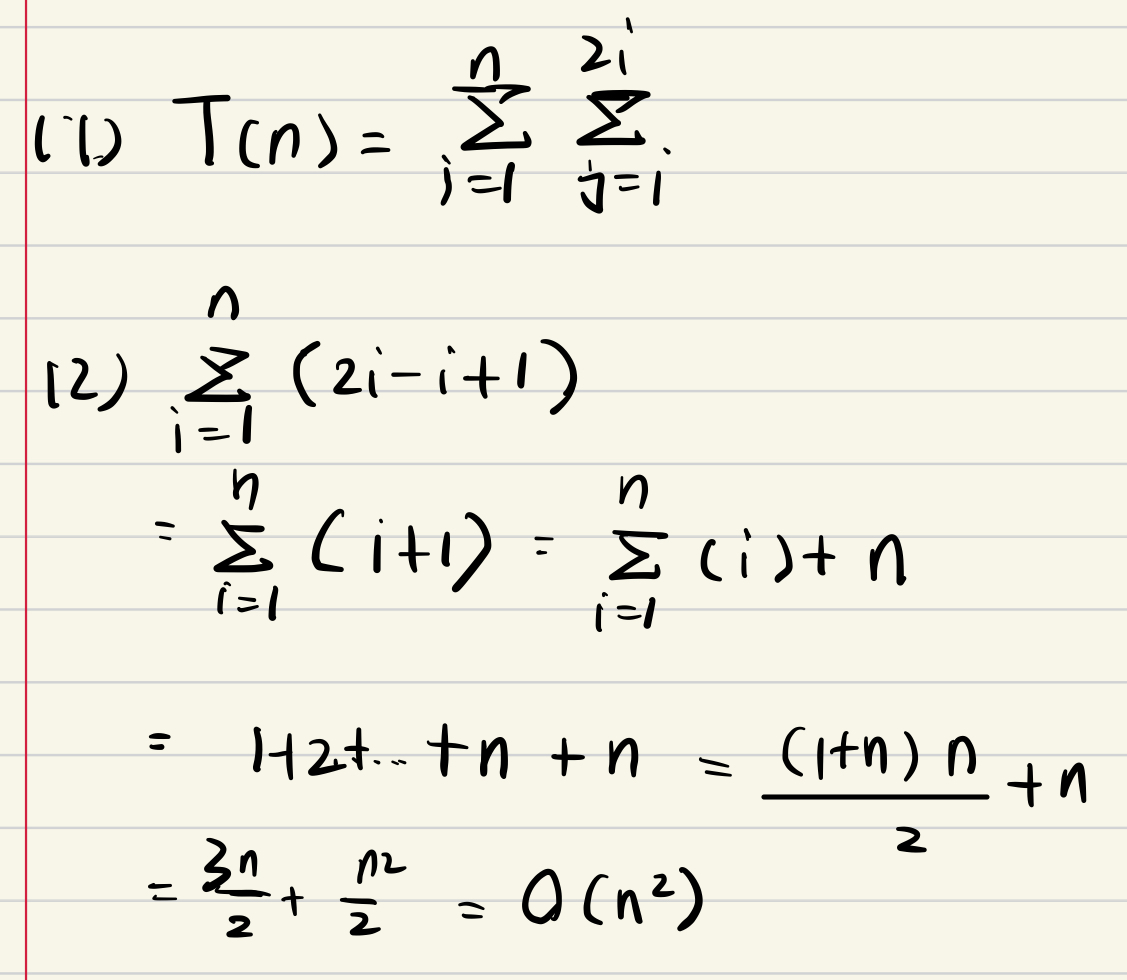
遞歸
e.g1*

后綴運算
主要考察的是棧
注意,減號的話是棧[-2]- 棧[-1]
?e.g1
(1)
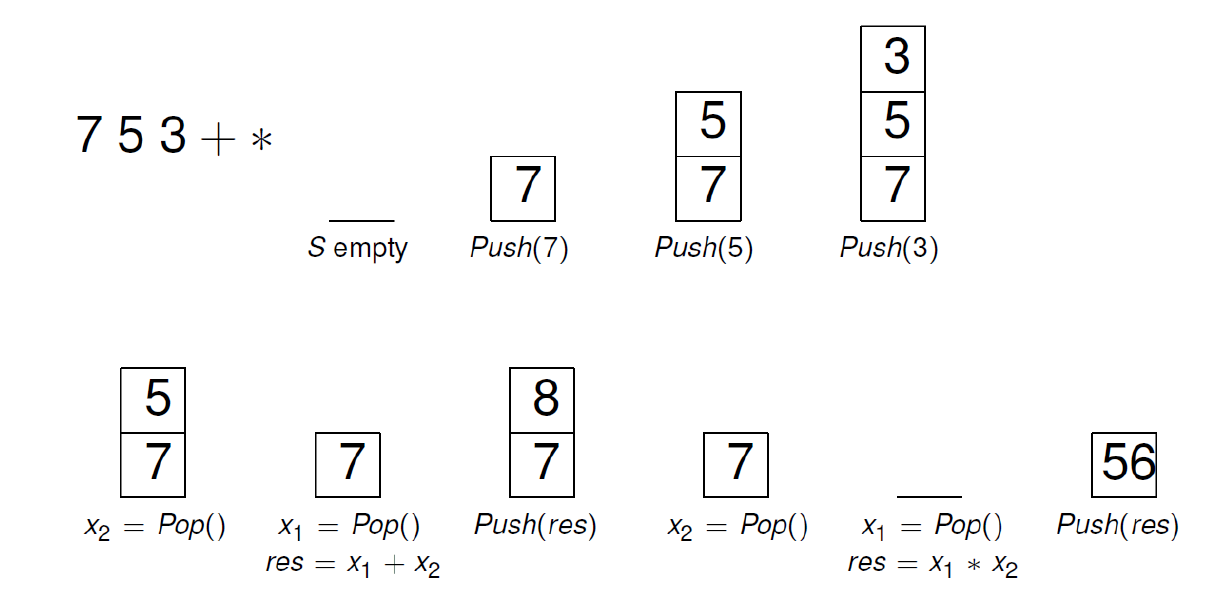
(2)

(3)
e.g2

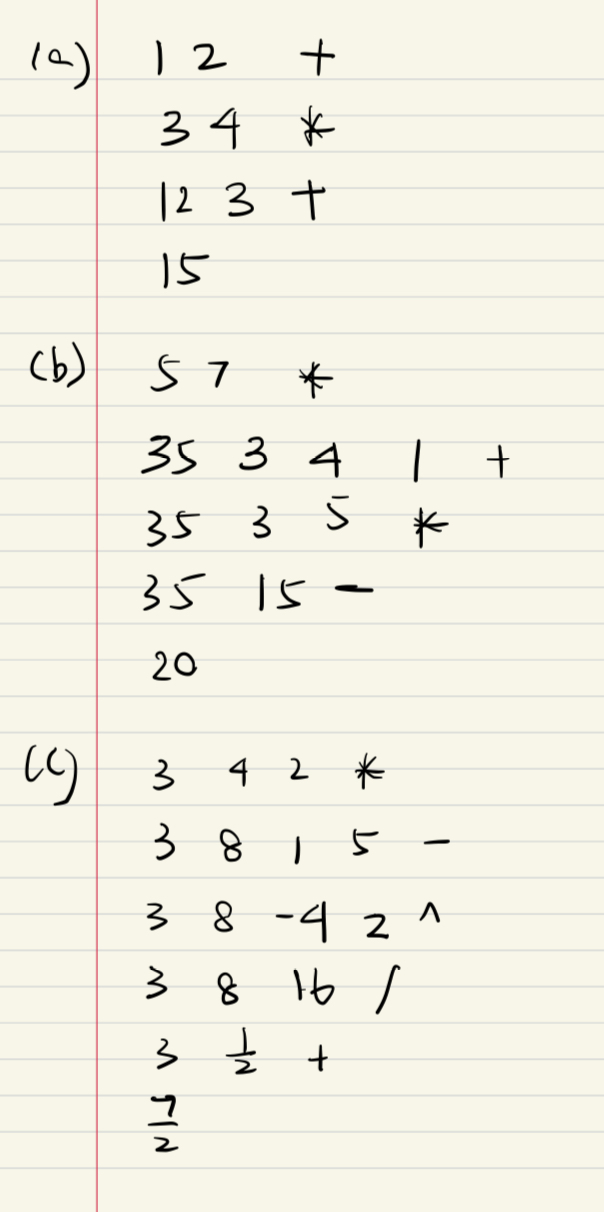
e.g3

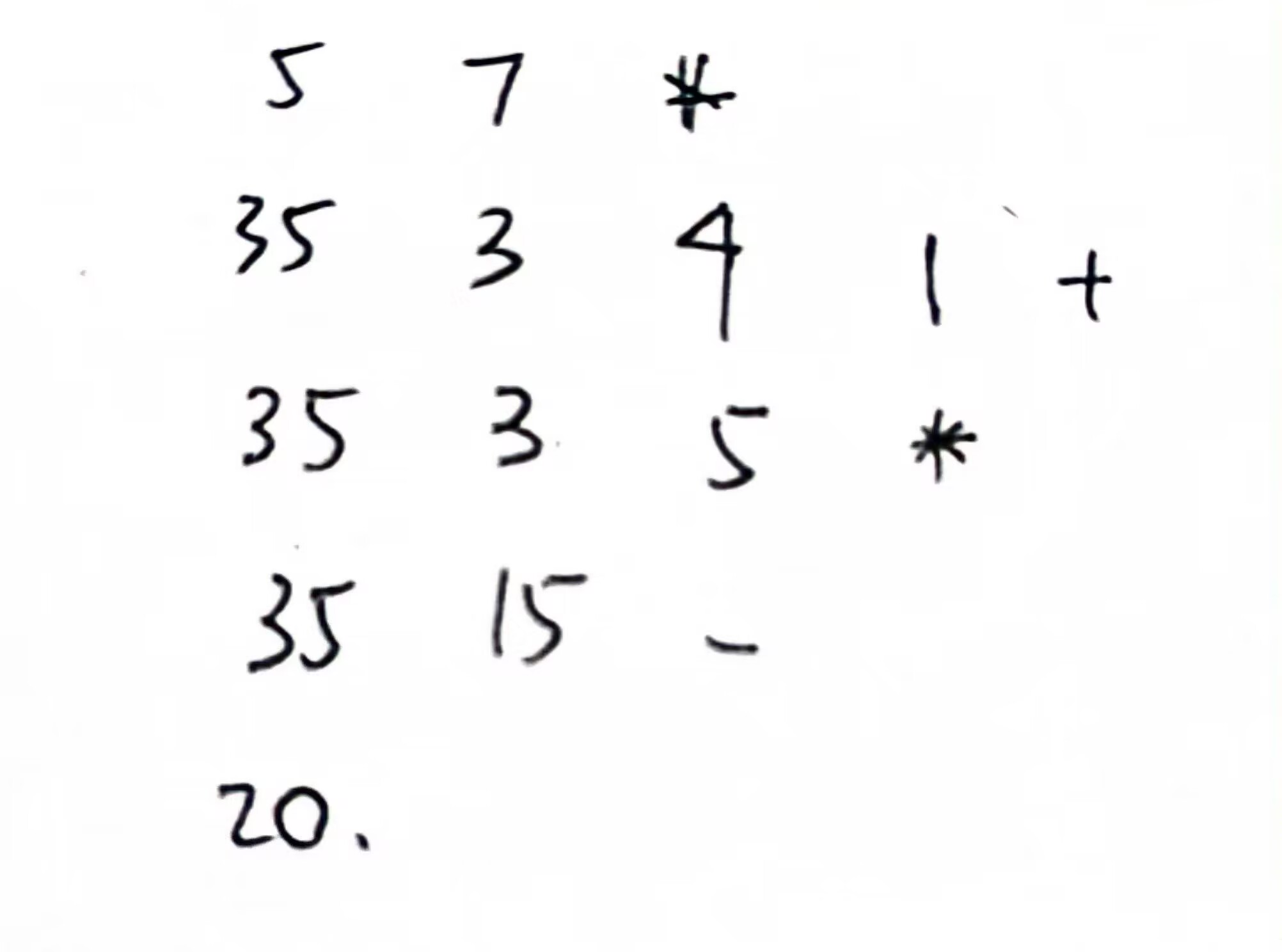
二叉樹
一個好用的數據可視化網站Data Structure Visualization
節點深度 O(n)
樹深度O(n)
查找O(n)(二分法)
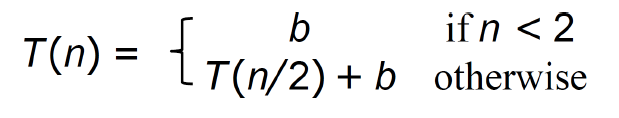
遍歷 O(n)
pre order 前序:中左右
in order中序:左中右
post order 后序:左右中
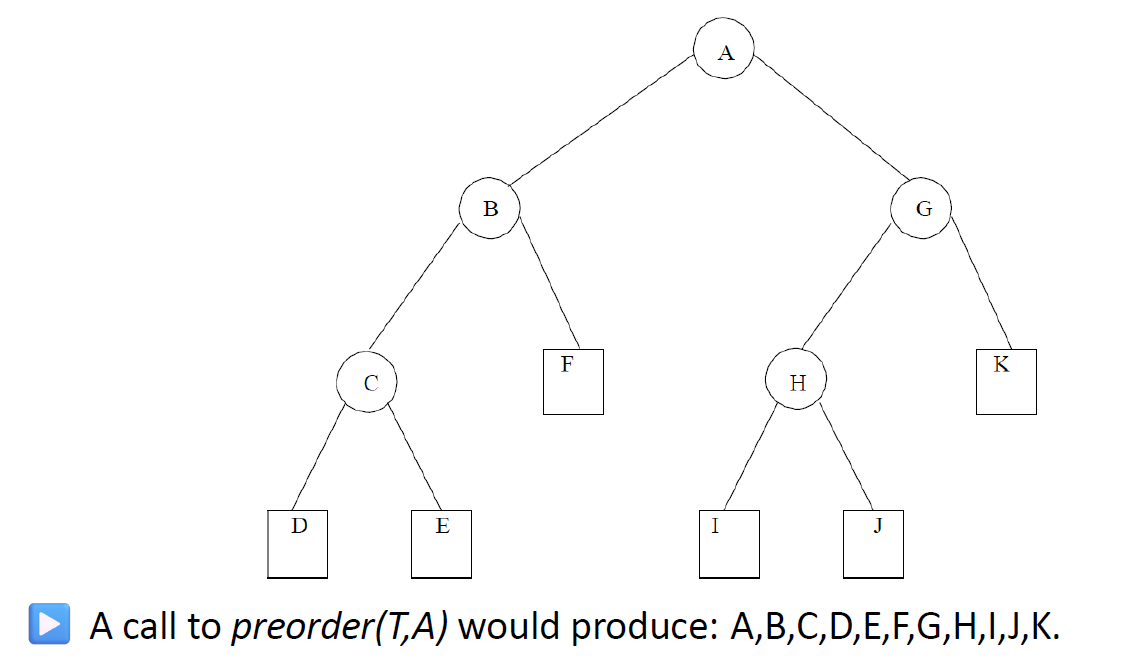

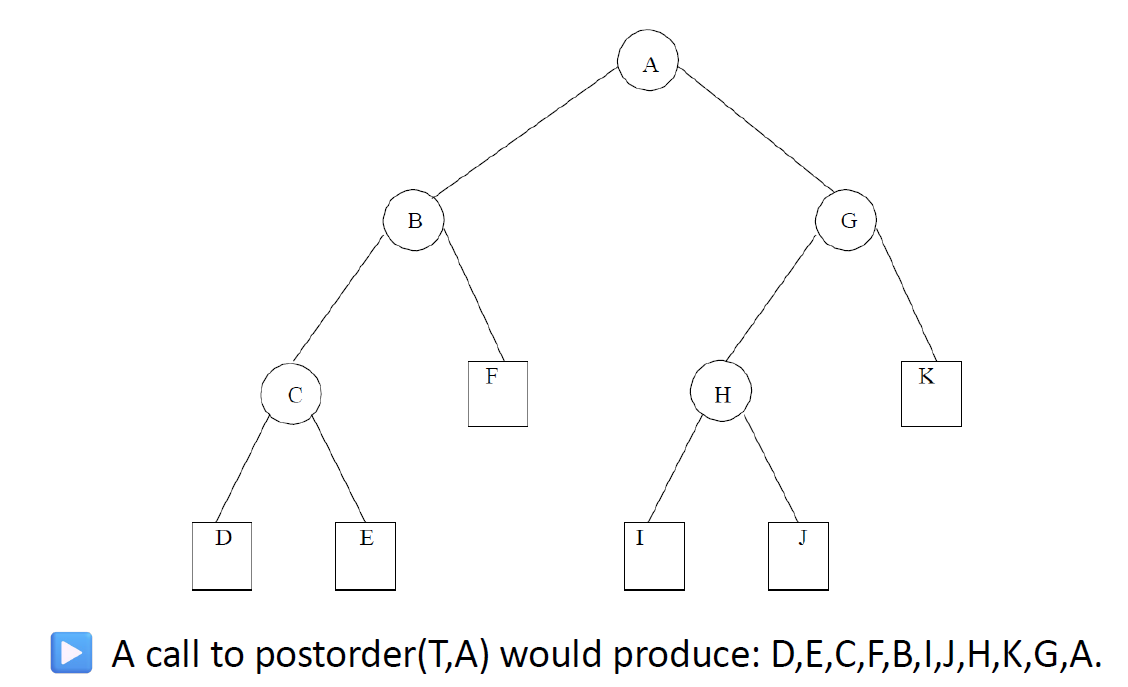
e.g1根據遍歷繪制樹

?
Binary search tree 二叉搜索樹
二叉搜索樹是一種特殊的二叉樹,具有以下性質:
對于每個節點 NNN:
所有左子樹節點的值都小于或等于節點 N的值
所有右子樹節點的值都大于節點 N的值
查找 O(logn)-O(n)
e.g1 節點能構成多少個二叉樹
用這個卡塔蘭公式得
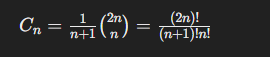

. - 力扣(LeetCode)
B
0/3 =5
1/2 =2
2/1 = 2
3/0 = 5
5+2+2+5=14
?AVL tree 平衡二叉樹
Height-Balance屬性: 對于任何節點n, n的左右子樹的高度最多相差1
All operations (search, insertion, and removal) on an AVL tree with n elements can be performed in O(log n)time
e.g1
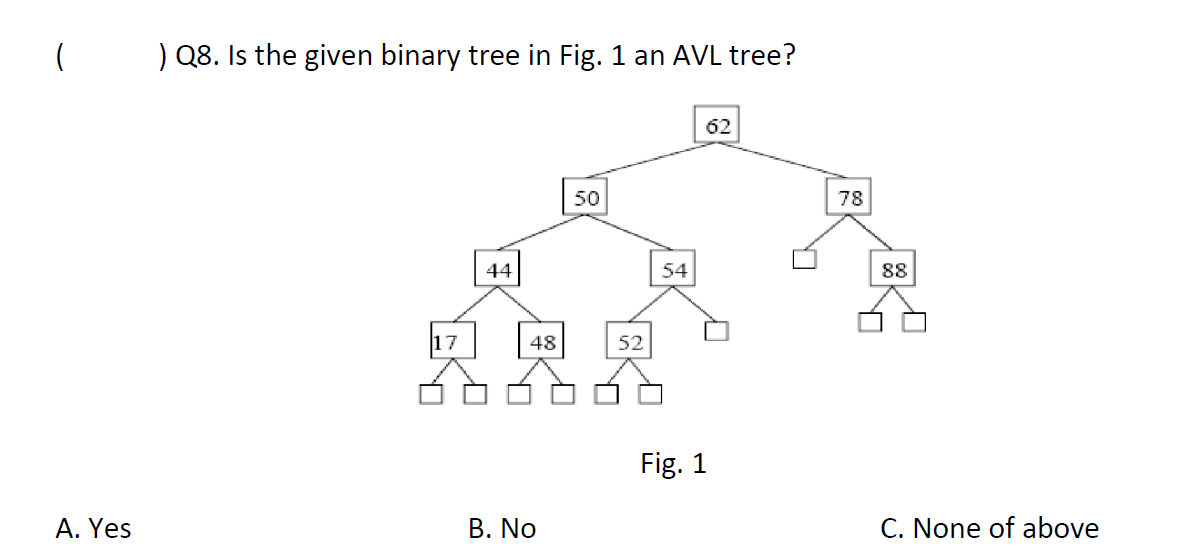
是的,左右節點響相差不超過1
添加節點O(log n)
是在樹枝的葉節點添加,再轉上去
集合進階-11數據結構(平衡二叉樹旋轉機制)_嗶哩嗶哩_bilibili
右邊多了左旋,左邊多了右旋
簡單情況:
以左旋為例:
?1)以不平衡點節點作為支點
2)把支點左旋降級,變成左子節點,晉升原來右子節點
復雜情況:
1)以不平衡點作為支點
2)將根節點右側往左拉
3)原先的右子節點變成新的父節點,并把多余的左子節點出讓,給已經降級的根節點當右子節點
四種情況:
- 左-左(LL)失衡:右旋。
- 右-右(RR)失衡:左旋。
- 左-右(LR)失衡:先左旋后右旋。
- 右-左(RL)失衡:先右旋后左旋。
e.g1 插入節點
插入節點后檢測平衡,刪除節點后面的節點頂替后檢查平衡
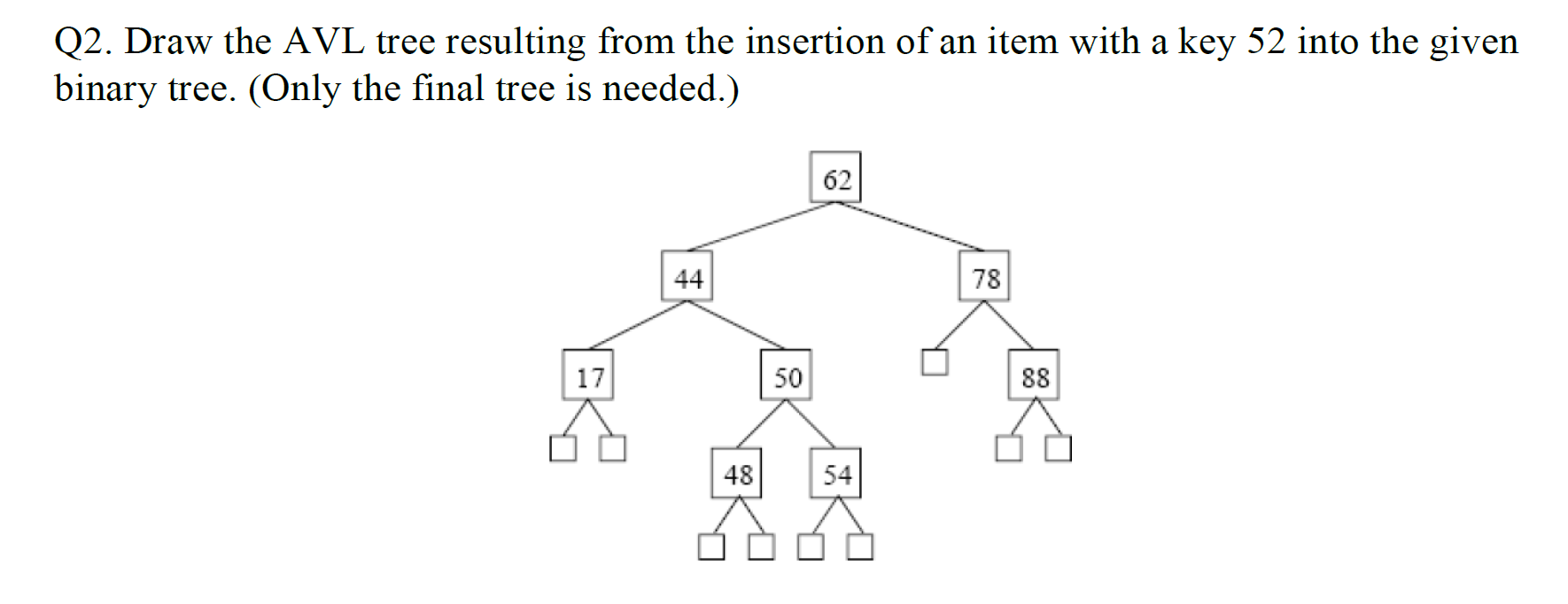
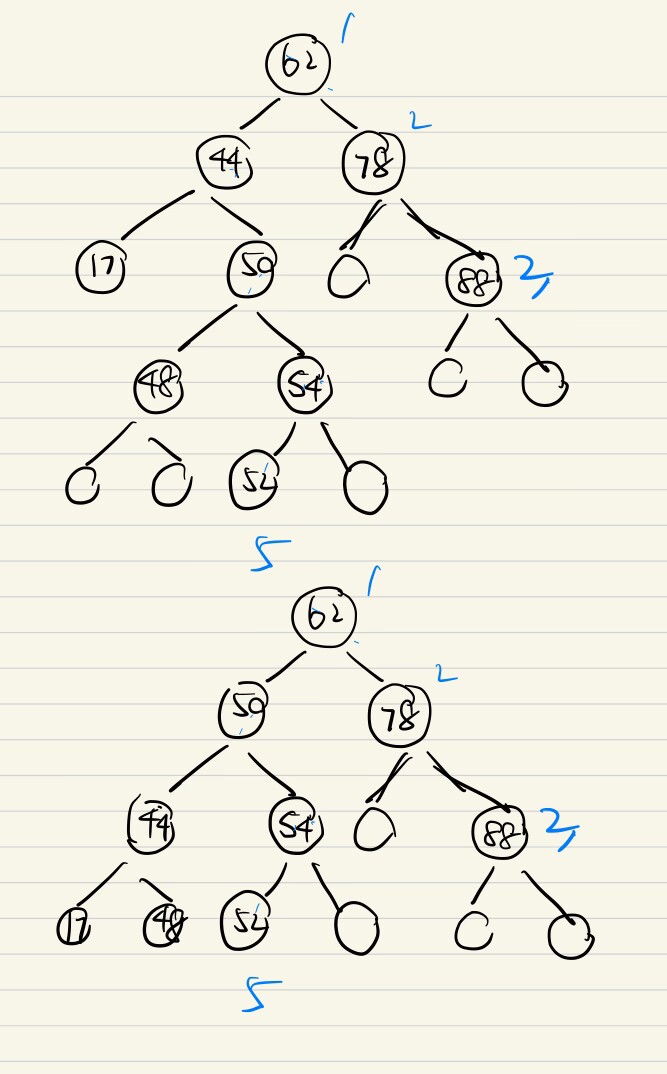
?
e.g3 構建AVL

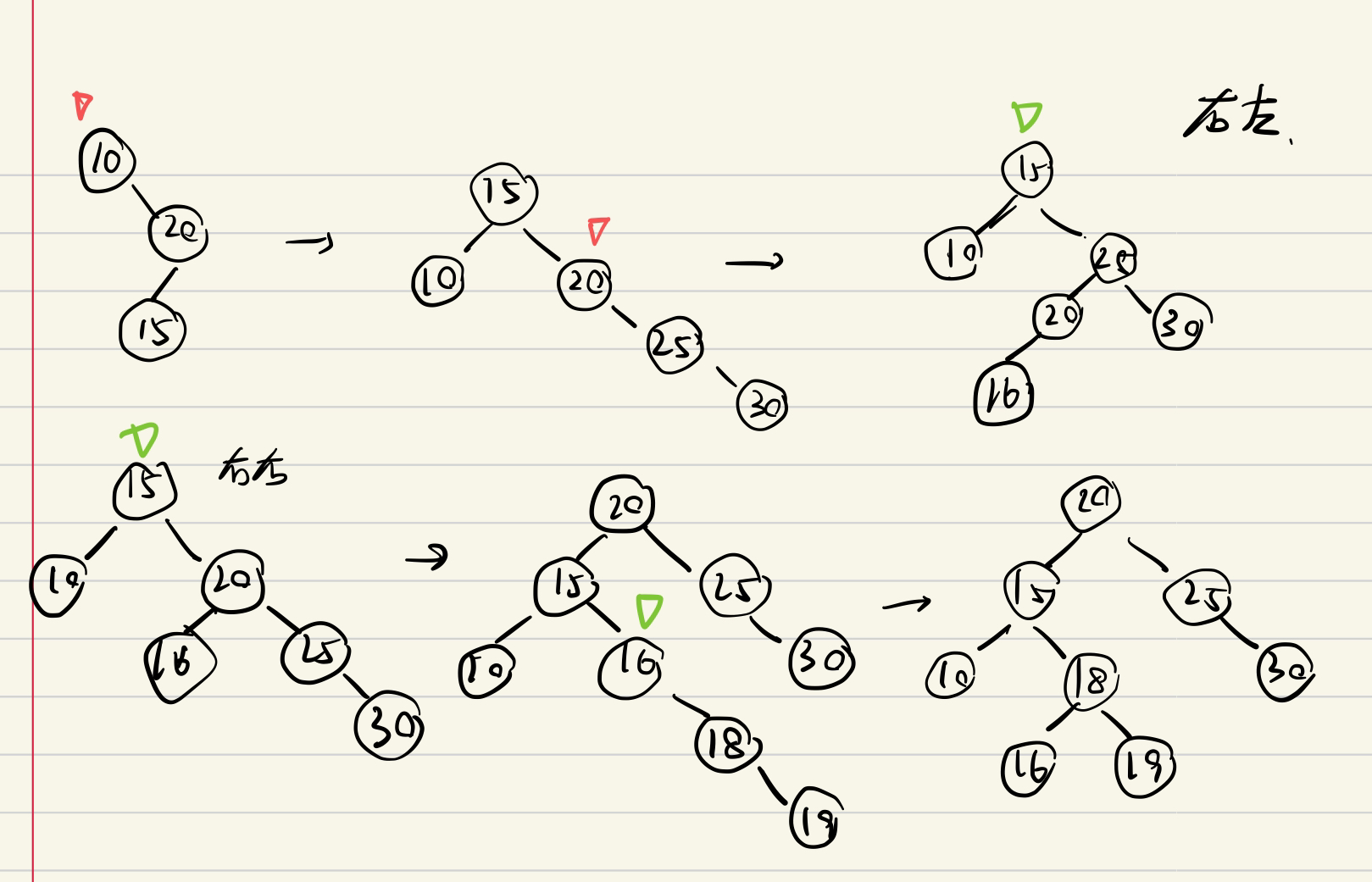
(2,4)樹
has height O(logn)
查找?O(logn)
(2,4)樹(也稱為2-4樹或2-3-4樹)是一種多路搜索樹,具有以下屬性:
節點大小屬性:每個內部節點最多有四個子節點
深度屬性:所有外部節點具有相同的深度
根據子節點的數量,(2,4)樹的內部節點被稱為2節點、3節點或4節點
注意,相同的元素產生的(2,4)樹可能會不一樣,取決于節點插入的順序
e.g1 樹高O(logn)
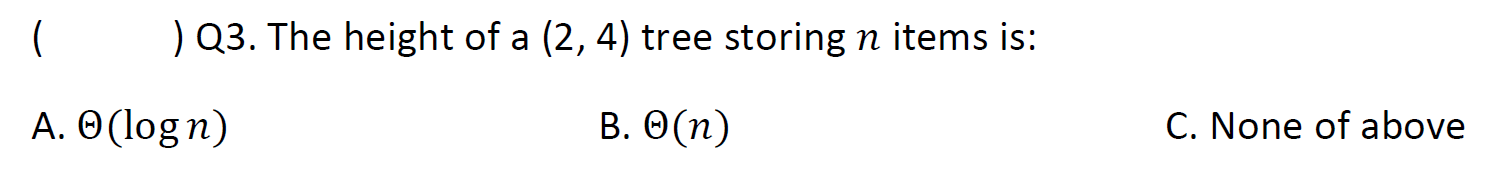
增O(logn)
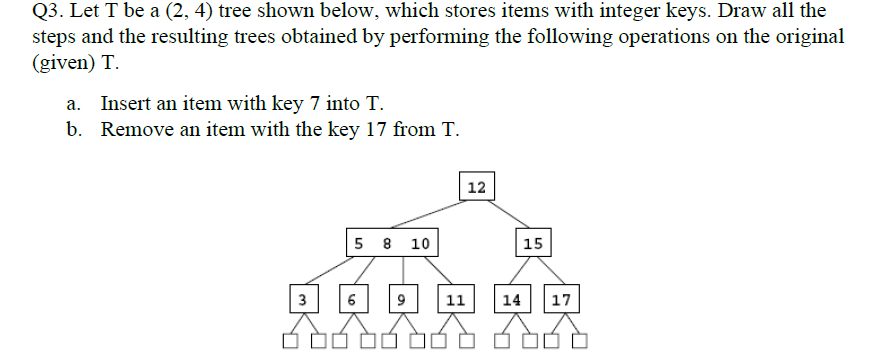
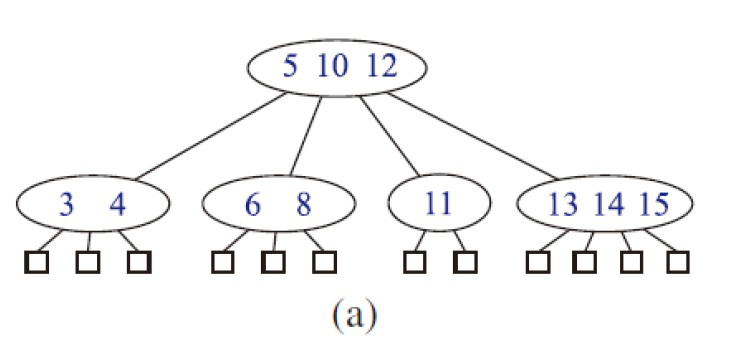
e.g1
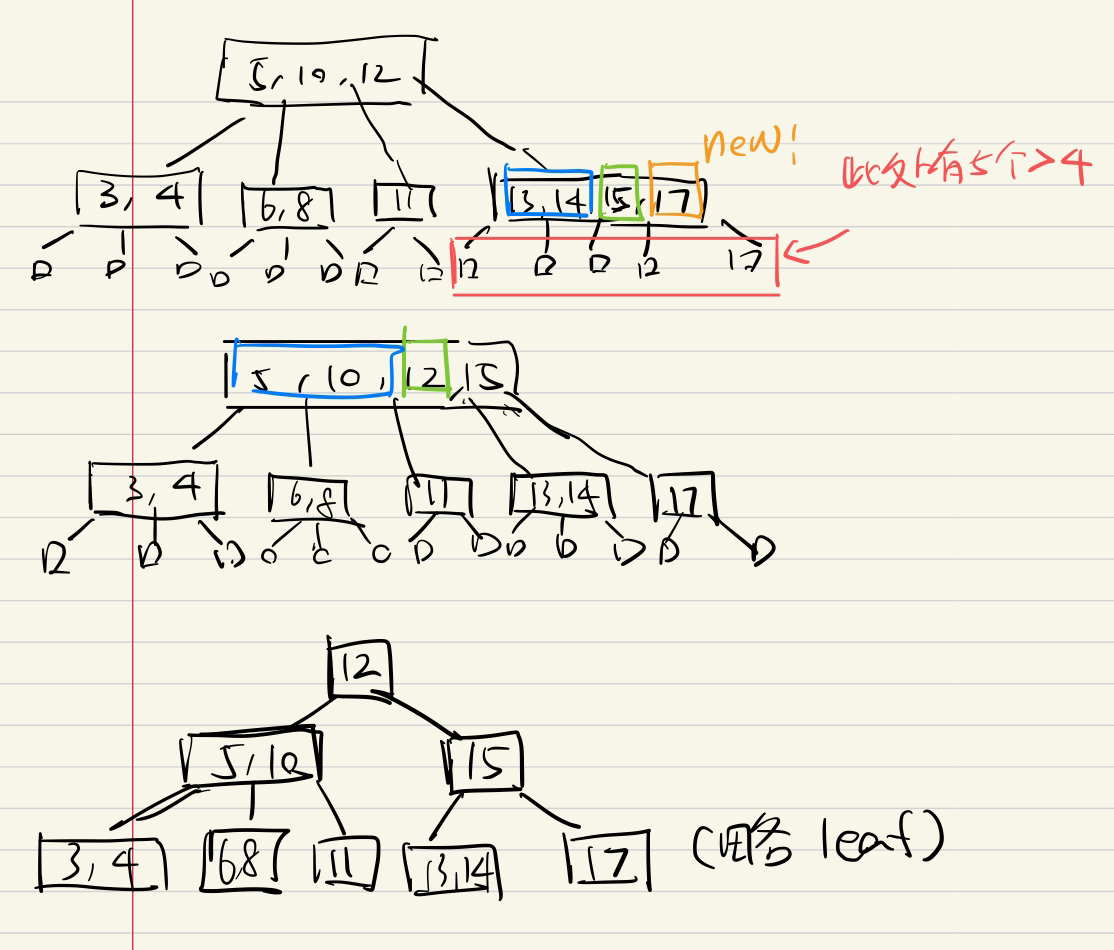
添加節點17
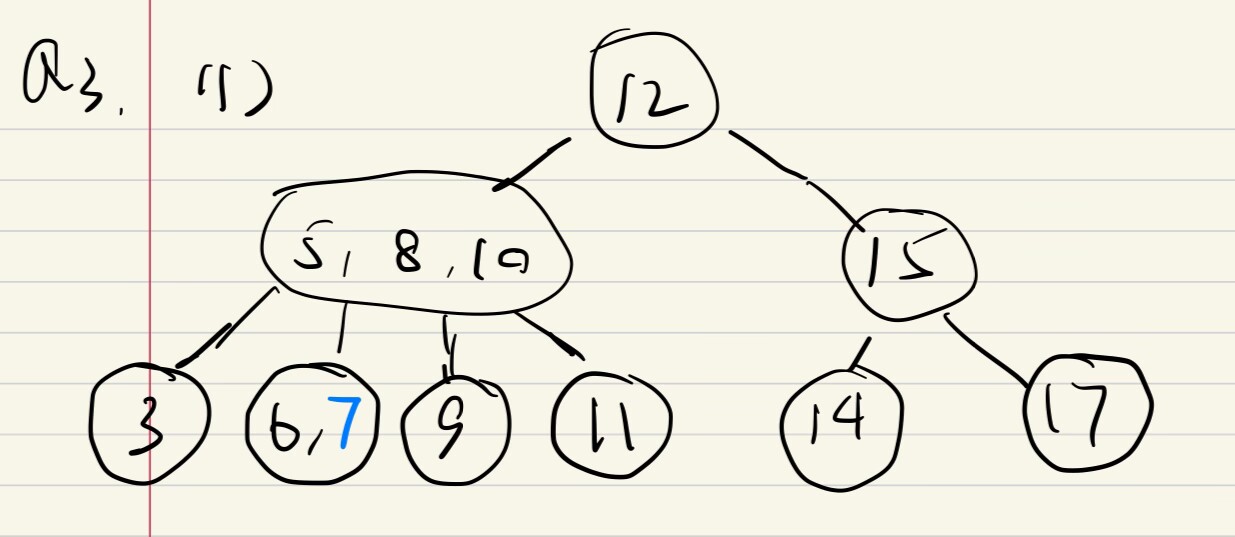
刪O(logn)
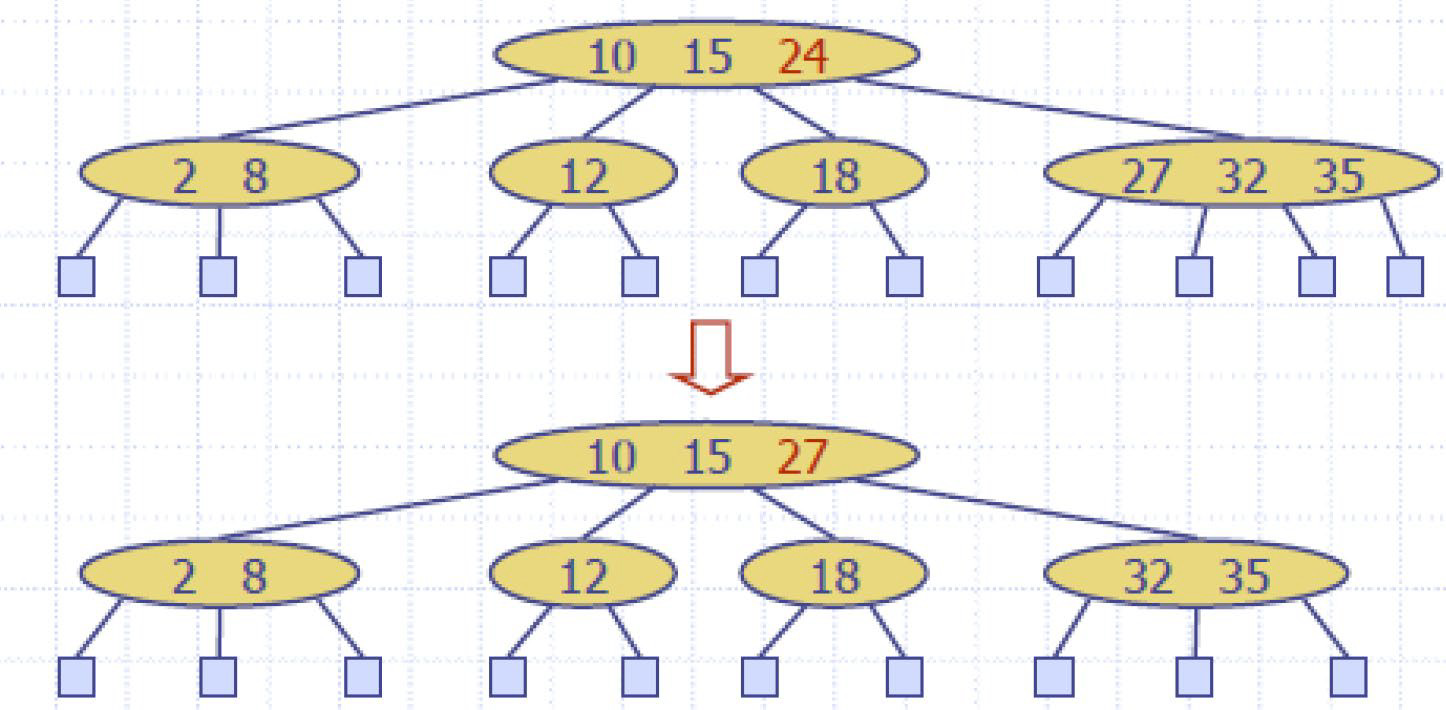

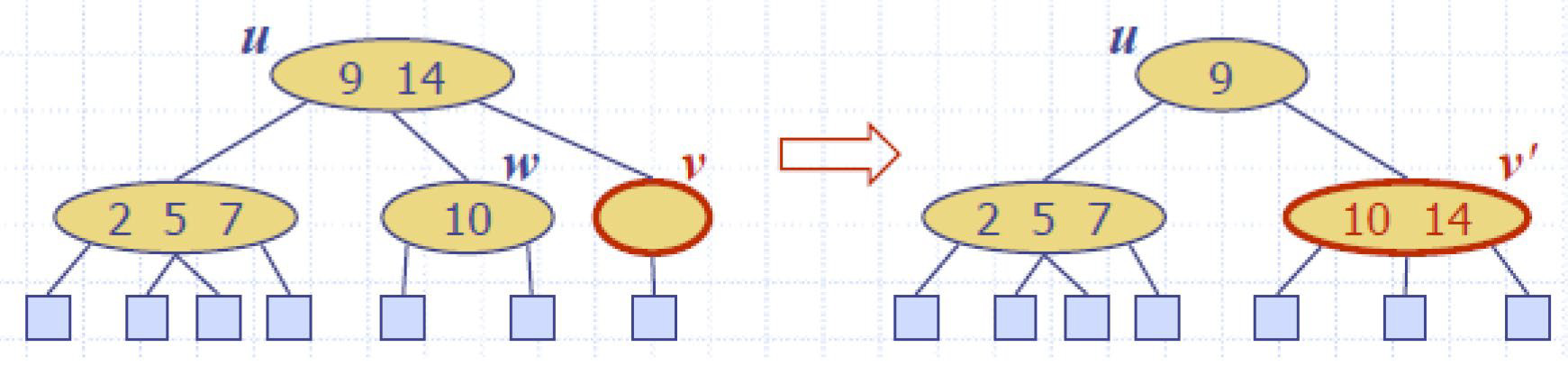

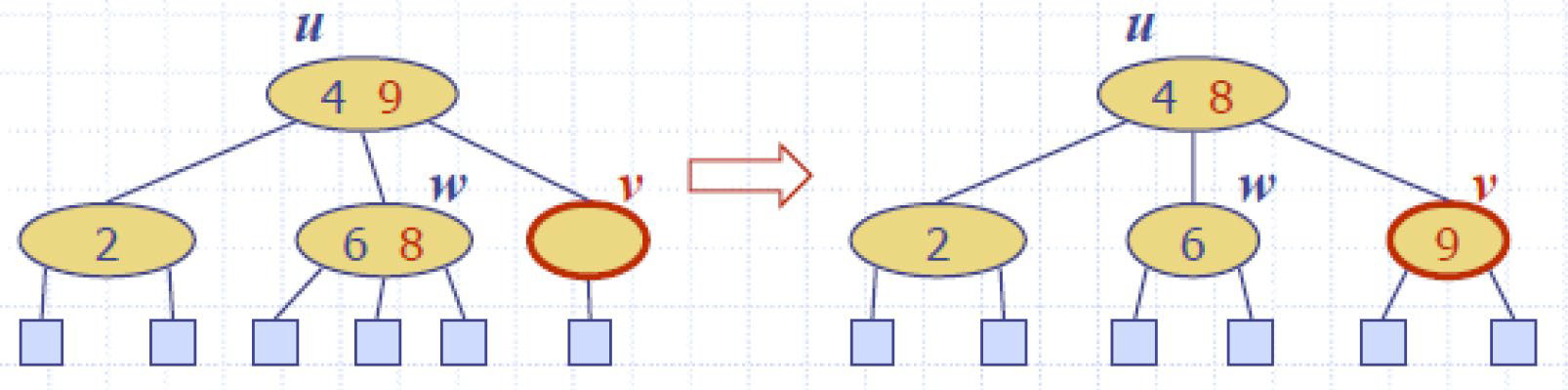
e.g2增/刪*
Heap 堆
【從堆的定義到優先隊列、堆排序】 10分鐘看懂必考的數據結構——堆_嗶哩嗶哩_bilibili
堆是一棵二叉樹,在其內部節點上存儲鍵,并滿足以下屬性:對于每個內部節點v,除了根節點key(v) ≥key(parent(v))
??節點中的鍵。
?父鍵不大于子鍵。
數組表示。
?索引從1開始。
?按等級順序獲取節點。
For any given node at position i:
??? ?Its Left Child is at [2*i] if available.
??? ?Its Right Child is at [2*i+1] if available.
??? ?Its Parent Node is at [?i/2?] if available.
因此,堆可以用數組表示,因為堆的下標和內容是一一對應的
注意,同[2,4]樹一樣,同一組數可能形成不同的堆
完全二叉樹?
沒有左子樹不能有右子樹
上一層沒有鋪滿,不能有下一層
優先隊列
堆是優先級隊列的一種實現,對于插入和刪除都是有效的。
新的元素插入隊列,彈出最小/最大元素O(logn)
可以進行排序,將隊列的元素依次彈出
max heap 大根堆,min heap 小根堆
?
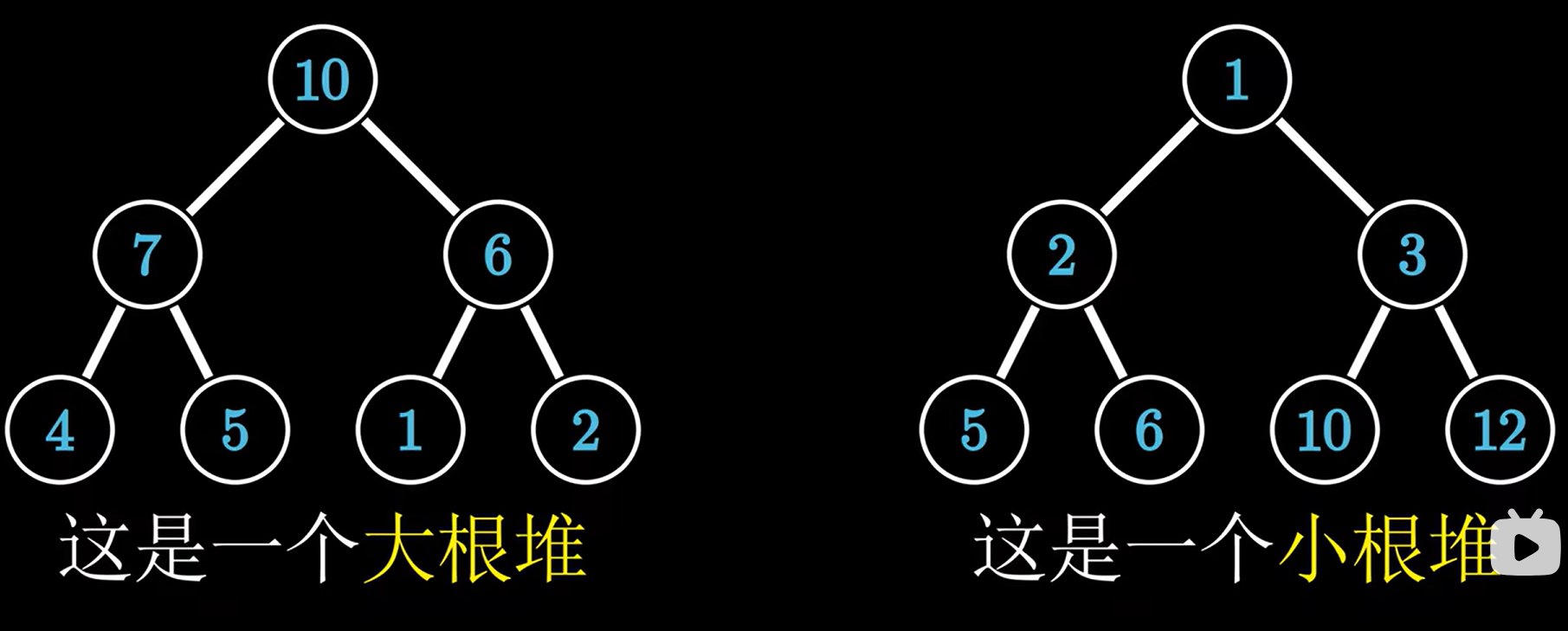
?e.g1
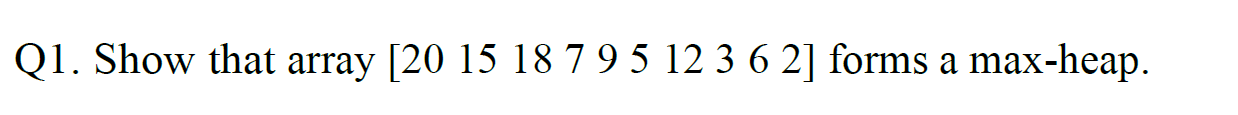
.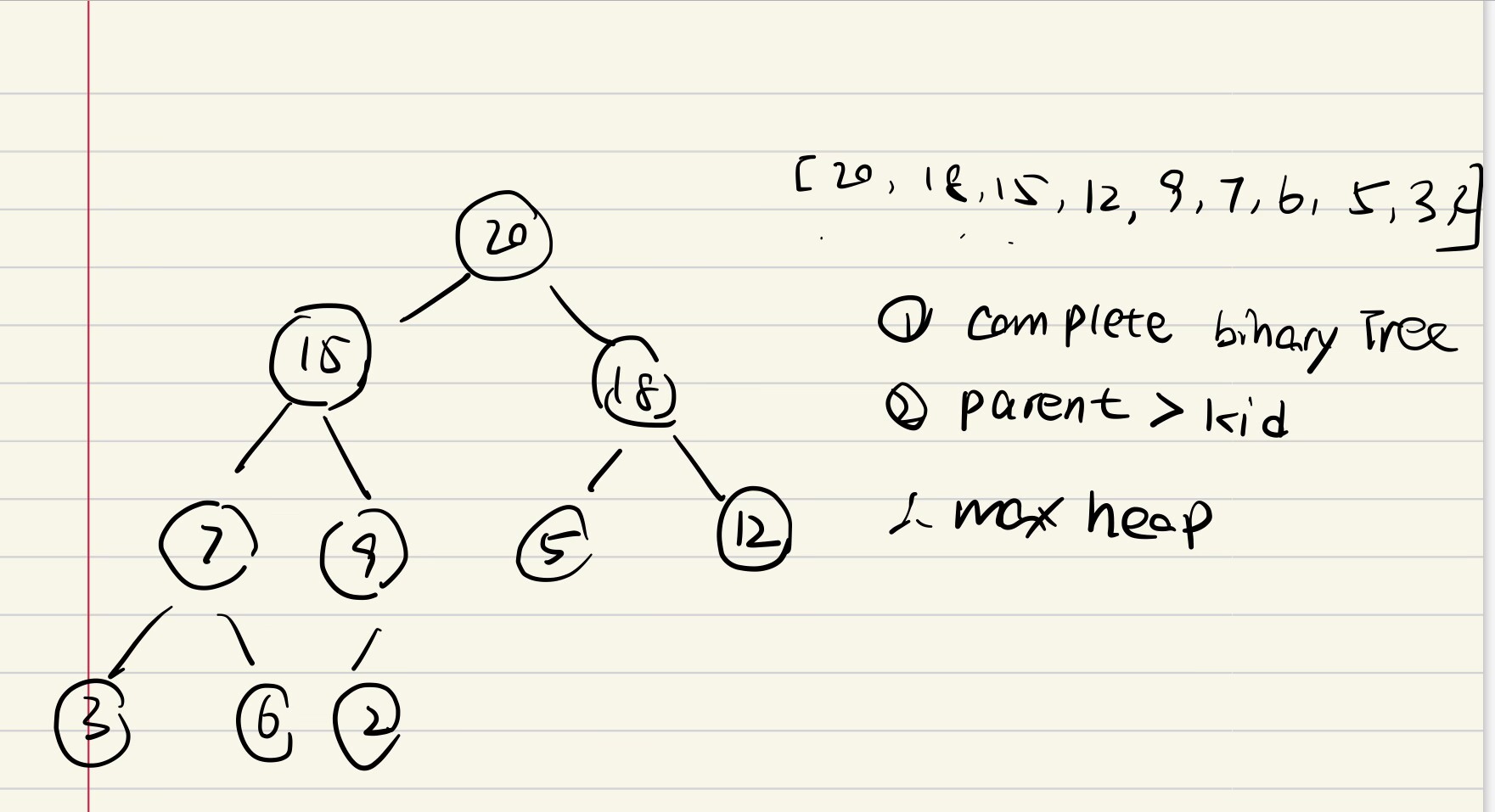
e.g2

C
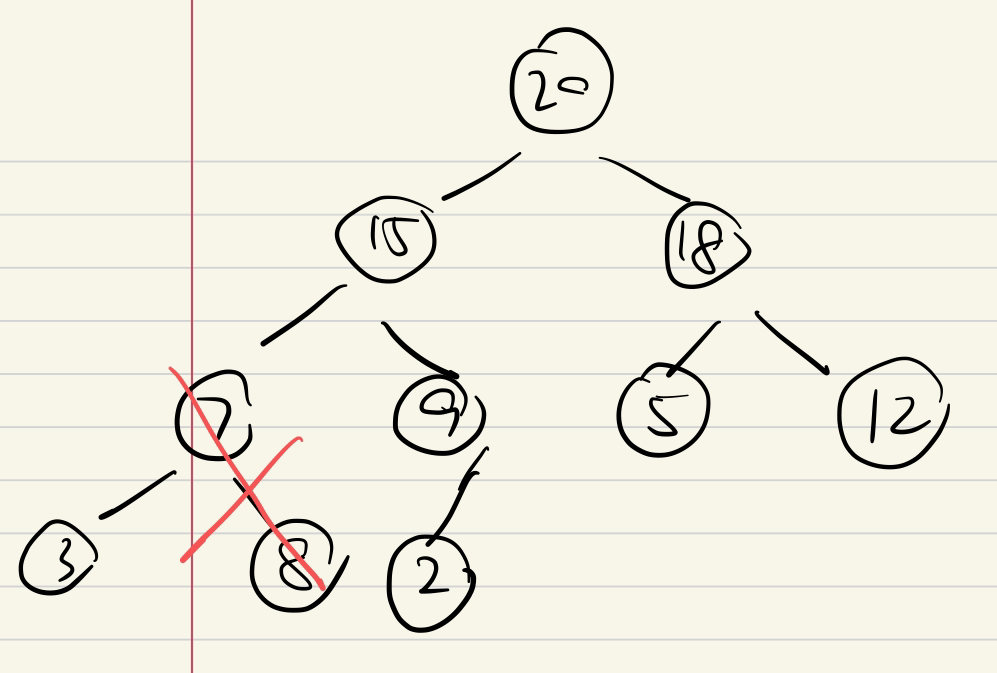
上/下濾?O(logn)
Up-heap bubbling 上濾
上濾用于插入新元素并維護堆的性質,將新元素逐級向上移動以確保其在正確的位置。
Down-heap bubbling 下濾
下濾用于刪除堆頂元素或修改堆頂元素后,重新調整堆的結構,將堆頂元素逐級向下移動以確保其在正確的位置。
注意在堆中,通常對于節點的下沉操作是有方向性的。對于最大堆(Max Heap),節點的下沉操作是沿著較大的子節點方向進行的,類似地,對于最小堆(Min Heap),節點的下沉操作是沿著較小的子節點方向進行的。
建堆
1)從葉節點插--上濾O(nlogn)
2) 先把數組中的數依次插入堆,然后再對每個父節點進行下率O(n)
(個人感覺考試的時候還是寫上濾會清楚一些)
e.g1
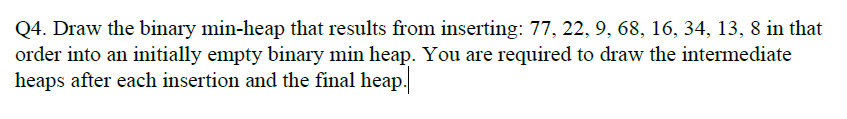
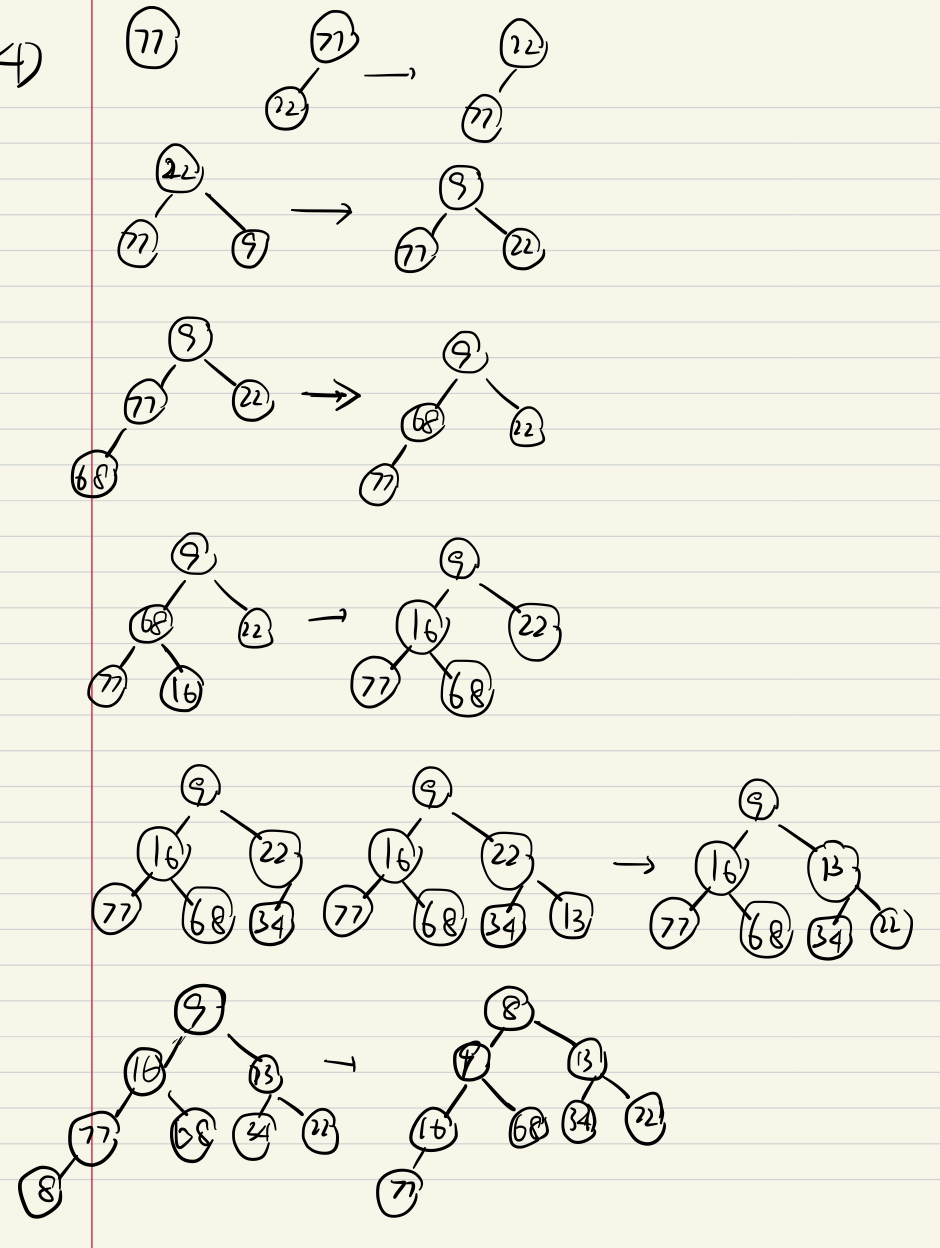
堆排序O(nlogn)
堆頂元素彈出后用最后一個元素堆疊到堆頂,然后下濾
大根堆下濾后變成小根堆,排序完是正序
小根堆下濾后變成大根堆,排序完是倒序
Lec8 分治法 Divide and conquer
分治法_嗶哩嗶哩_bilibili
將一個規模為n的問題u分解為k個規模為較小的子問題,子問題相互獨立且與原問題相同,遞歸地求解這些子問題,然后利用子問題的解合并構造出原問題的解
設計:分解(Divide);遞歸求解(Conquer);合并(Combine)
分析:
1.建立遞歸方程T(n)?= aT(n/b)+f(n)
2.求解遞歸方程T(n)
Sort
MergeSort

QuickSort

Master Method 主定理
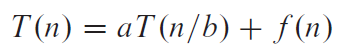

e.g1 case1
直接套公式
我寫的
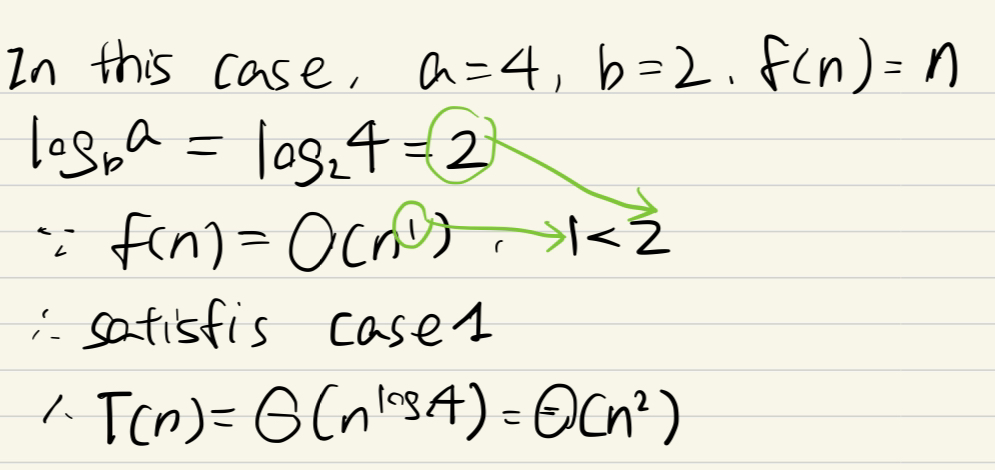
標答:
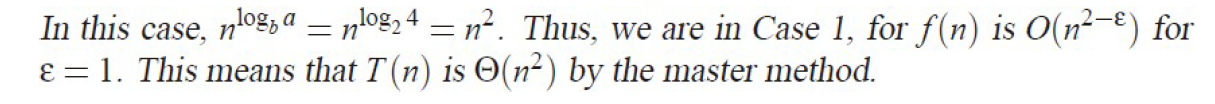
e.g2 case2
直接套公式
![]()
我寫的
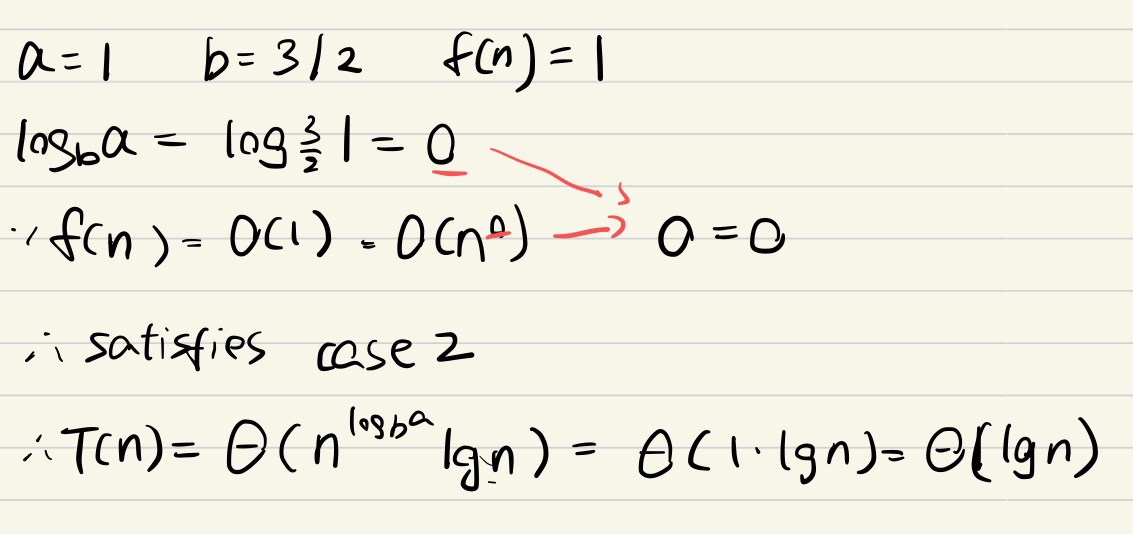
標答
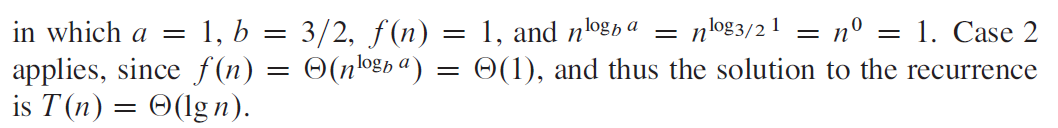
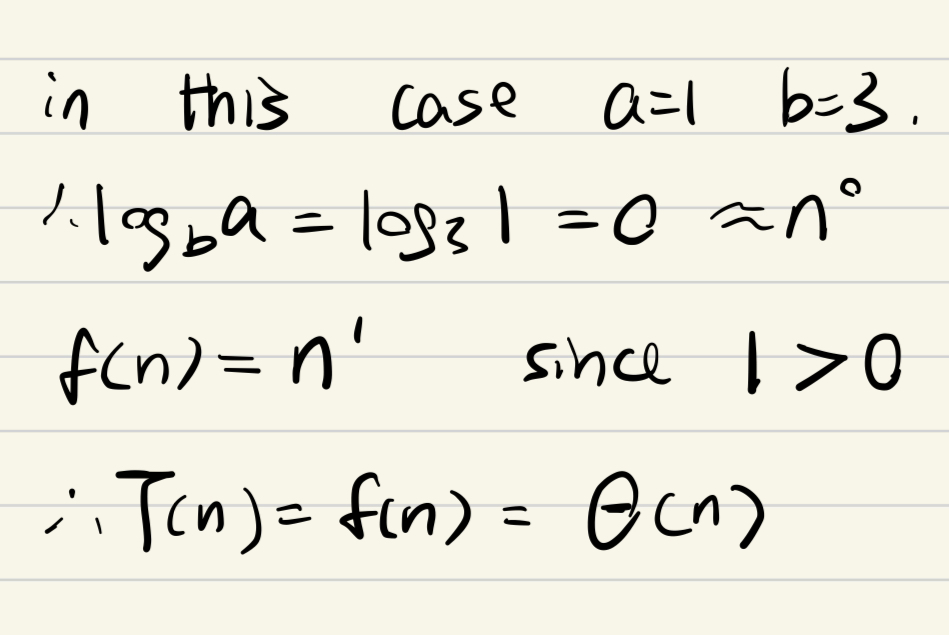
e.g3 case3
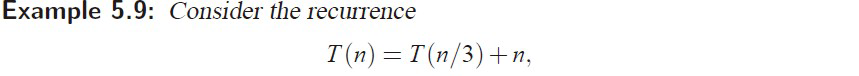
?標答
e.g4 注意lgn有坑!*****

?標答
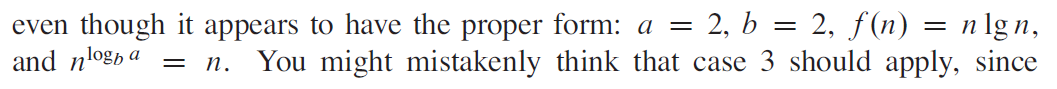
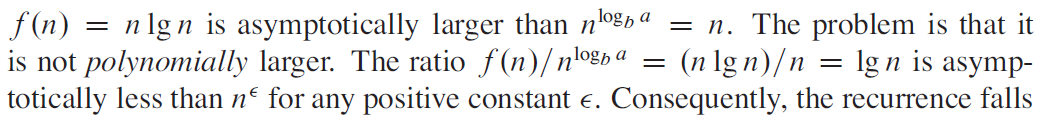
e.g5 同e.g4
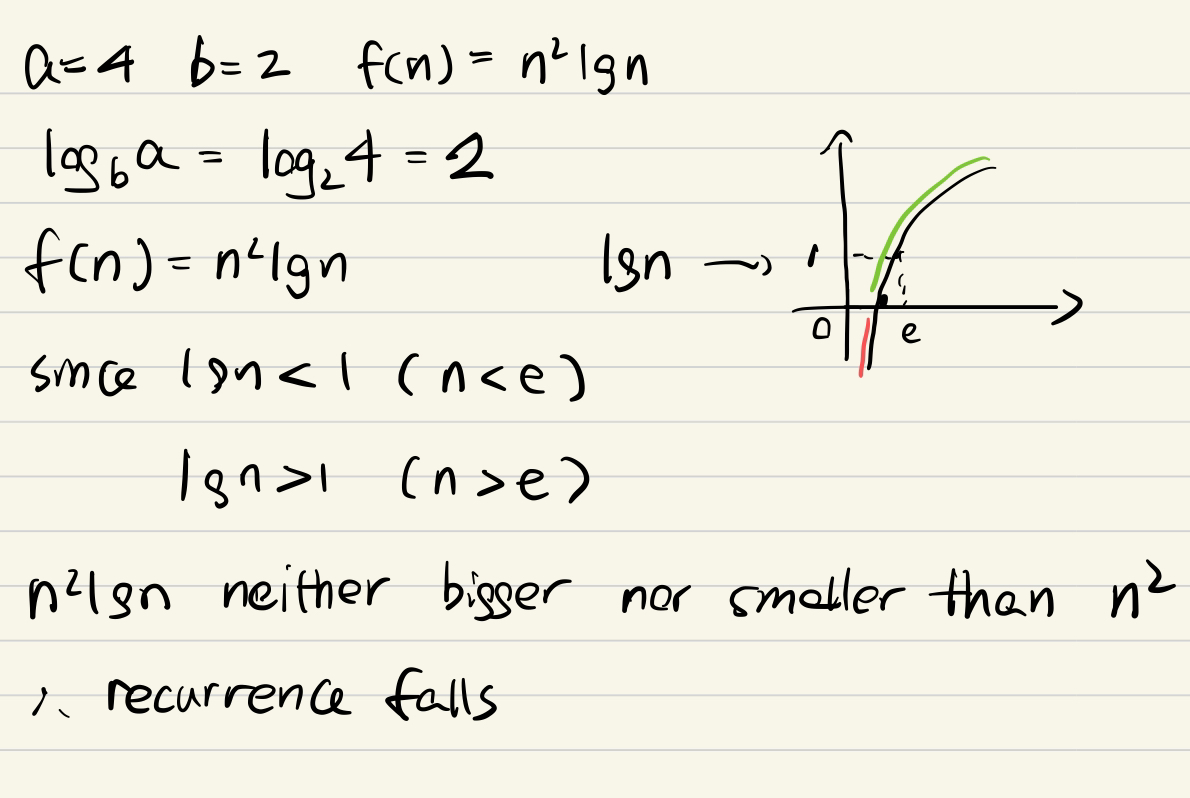
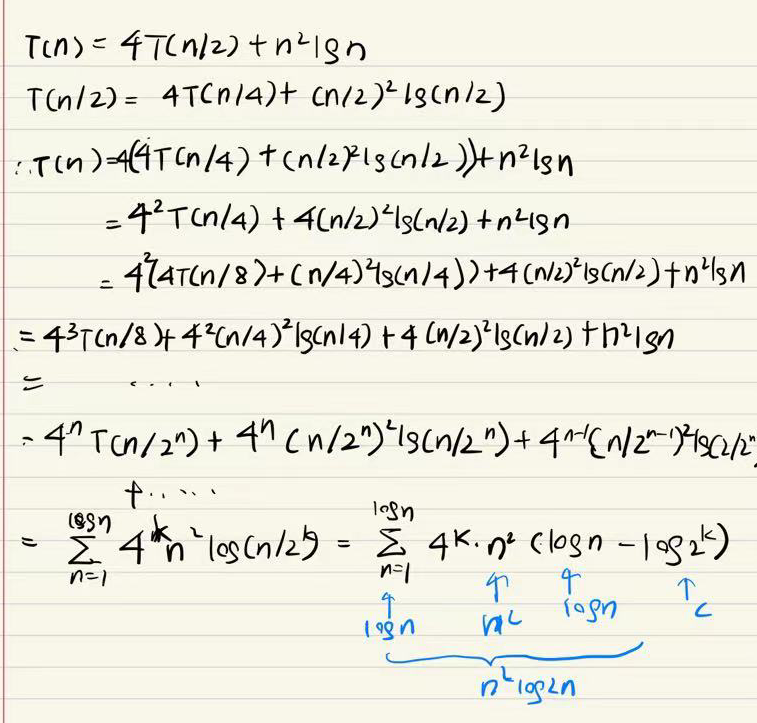
e.g6***不符合Master method
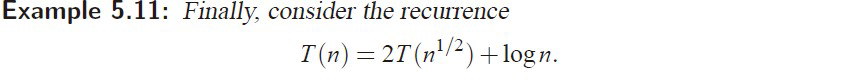


Matrix Multiplication 矩陣乘法???(暫時擱)
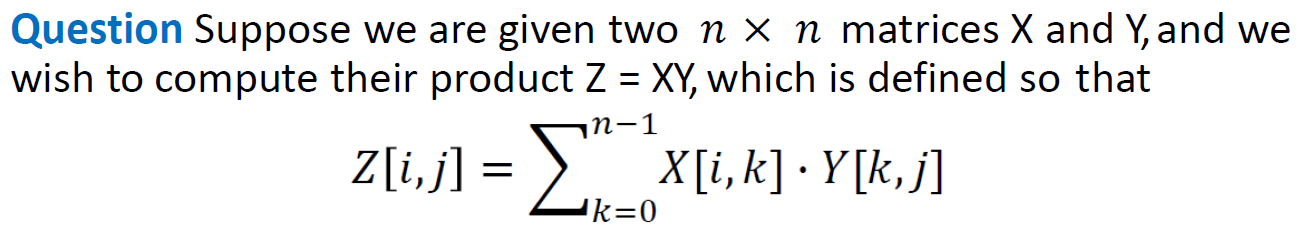
Counting inversion???(暫時擱)
Lec9 最優化問題
Knapsack 背包問題
?fractional 背包
e.g1
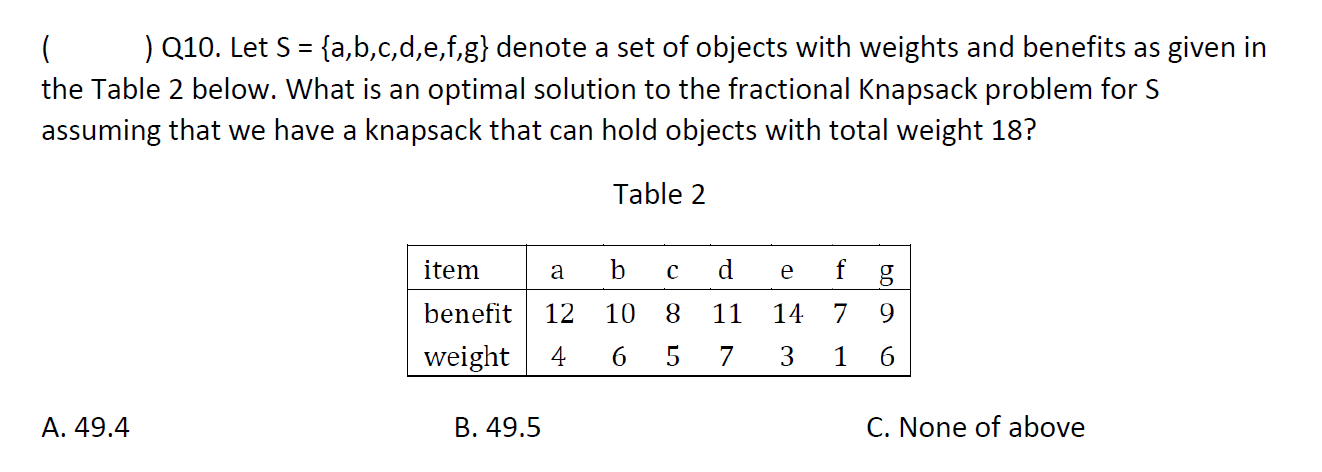
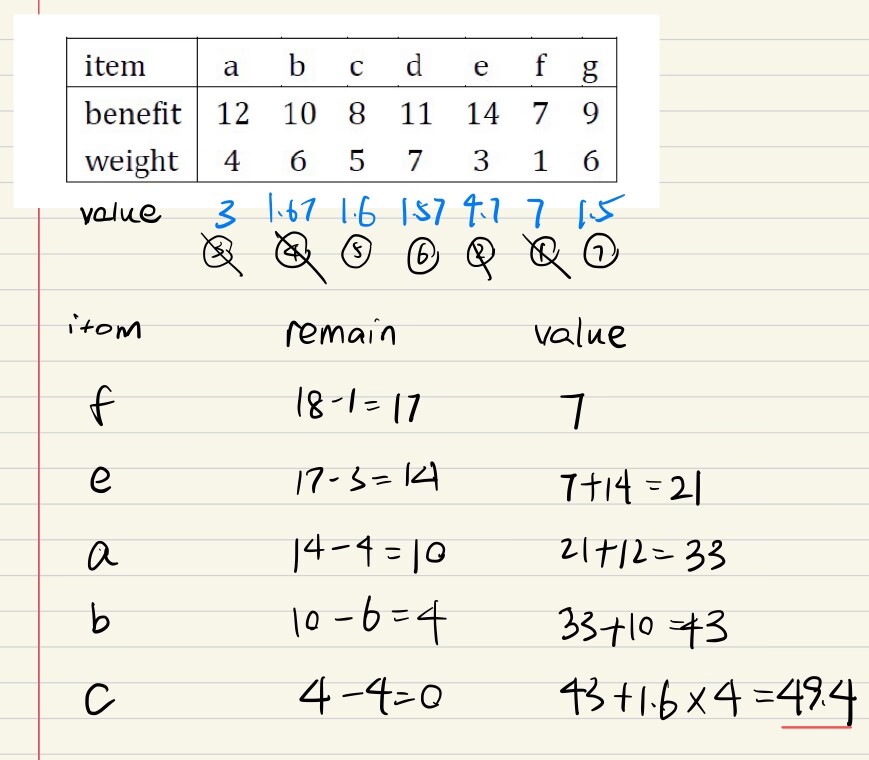
01背包
0/1背包問題-動態規劃 Knapsack_problem Dynamic Programming_嗶哩嗶哩_bilibili
https://alchemist-al.com/algorithms/knapsack-problem
e.g1?
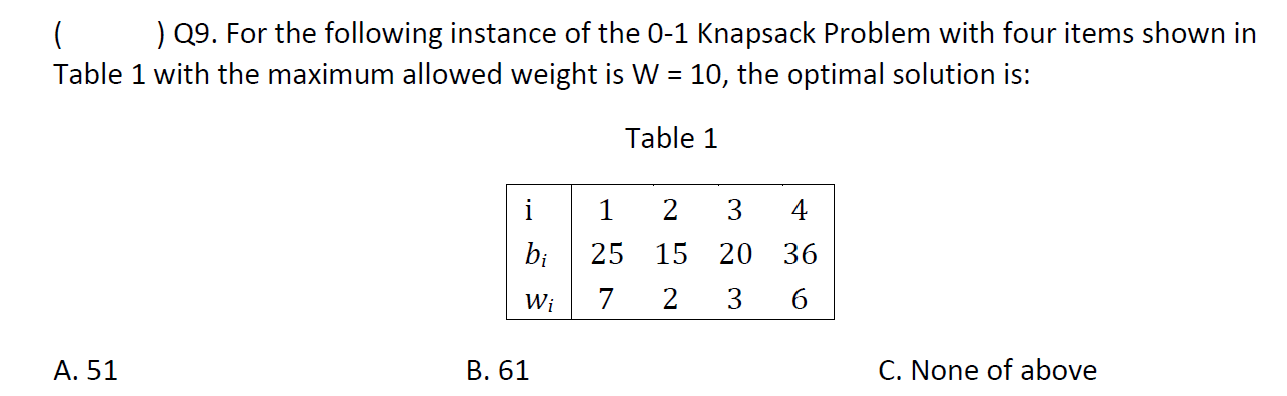
C
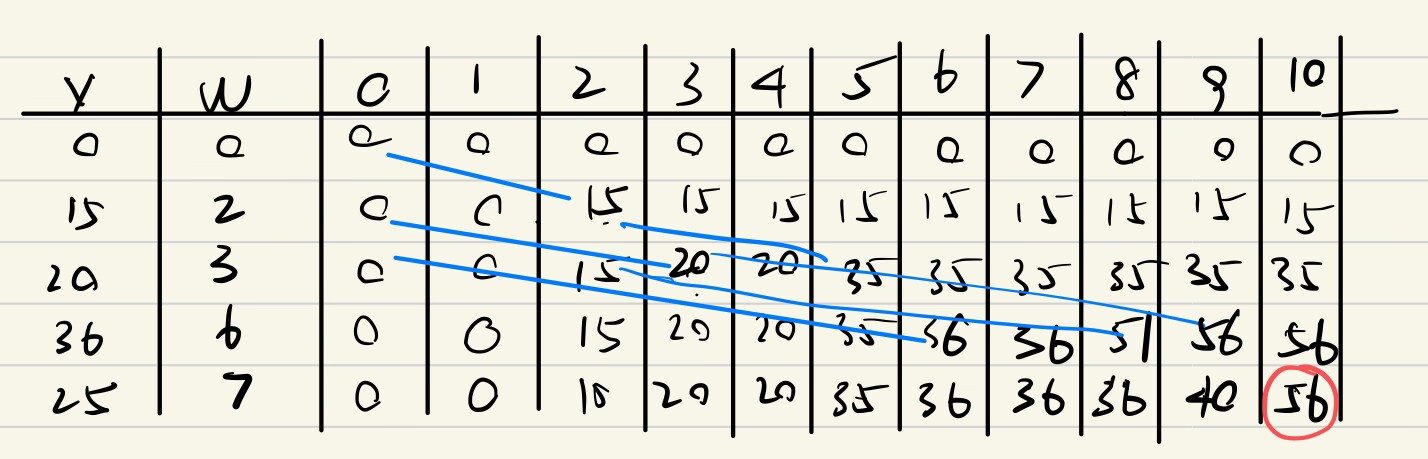
e.g2

我做的,我習慣先按照重量排序一下再算
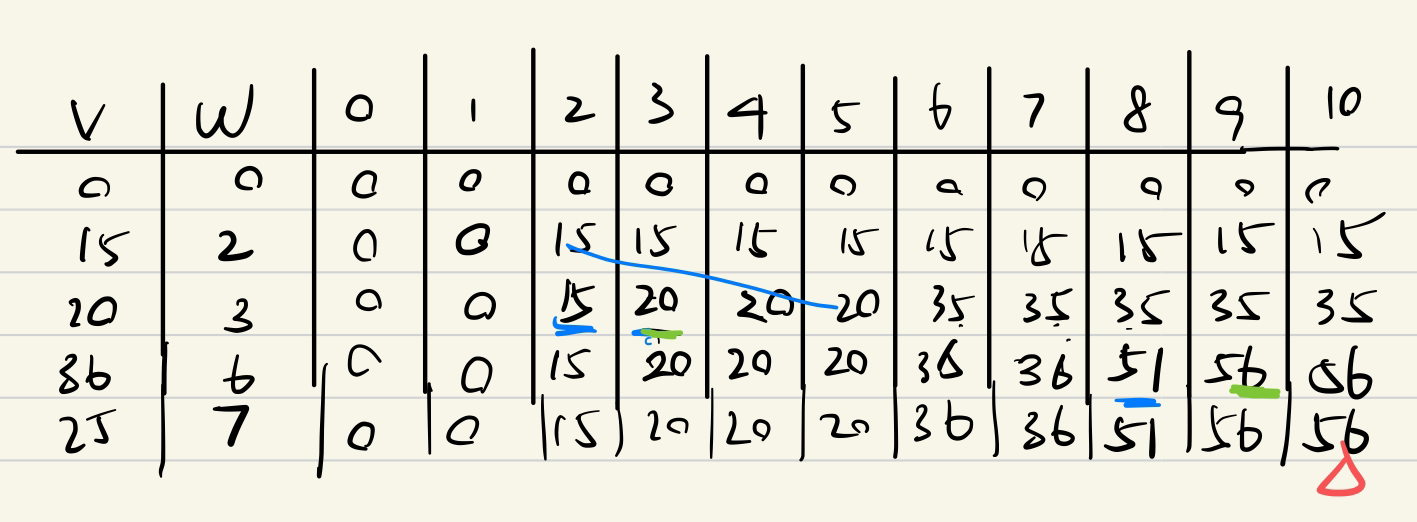
標答
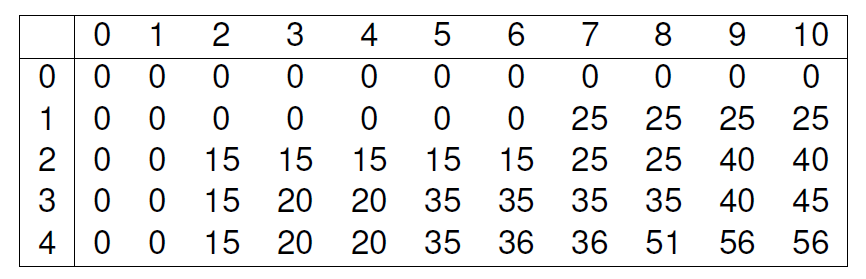
Interval Scheduling 區間調度(暫時擱置)
動態規劃——區間DP_嗶哩嗶哩_bilibili
?大題***
![]()

Lec10 Graph
A graph𝐺=𝑉,𝐸consists of a set of vertices (nodes) V and a set of edges E, where each 𝑒∈𝐸 is specified by a pair of vertices 𝑢,𝑣∈𝑉
一些術語
End vertices:一條邊的頂點
Edges incident:一個頂點相鄰的邊
Adjacent vertices:相鄰的頂點
Degree:是指一個頂點連接的邊的數量
Path:交替的頂點和邊的序列,從頂點開始,以頂點結尾,每條邊的前面和后面都有它的sendpoints?
Simple Path:所有頂點和邊都不相同的路徑
subgraph:子圖
acyclic graph: 沒有 cycle的圖。樹是相互連接的acyclic graph
Directed acyclic graphs 有向無環圖稱為dag。不可能通過遍歷這些邊回到同一個節點。
-
最小生成樹:用于找到一個圖中連接所有頂點的最小權重的樹。常用的算法包括Prim算法和Kruskal算法。這些算法主要關注于連接所有頂點,而不是特定的起點和終點。
-
最短路徑:用于找到圖中從一個頂點到另一個頂點的最短路徑。常用的算法包括Dijkstra算法和Bellman-Ford算法。這些算法主要關注于找到從一個指定起點到一個指定終點的最短路徑。
Dijkstra
記錄總路徑,當然是要從最短的來s

我自己做的
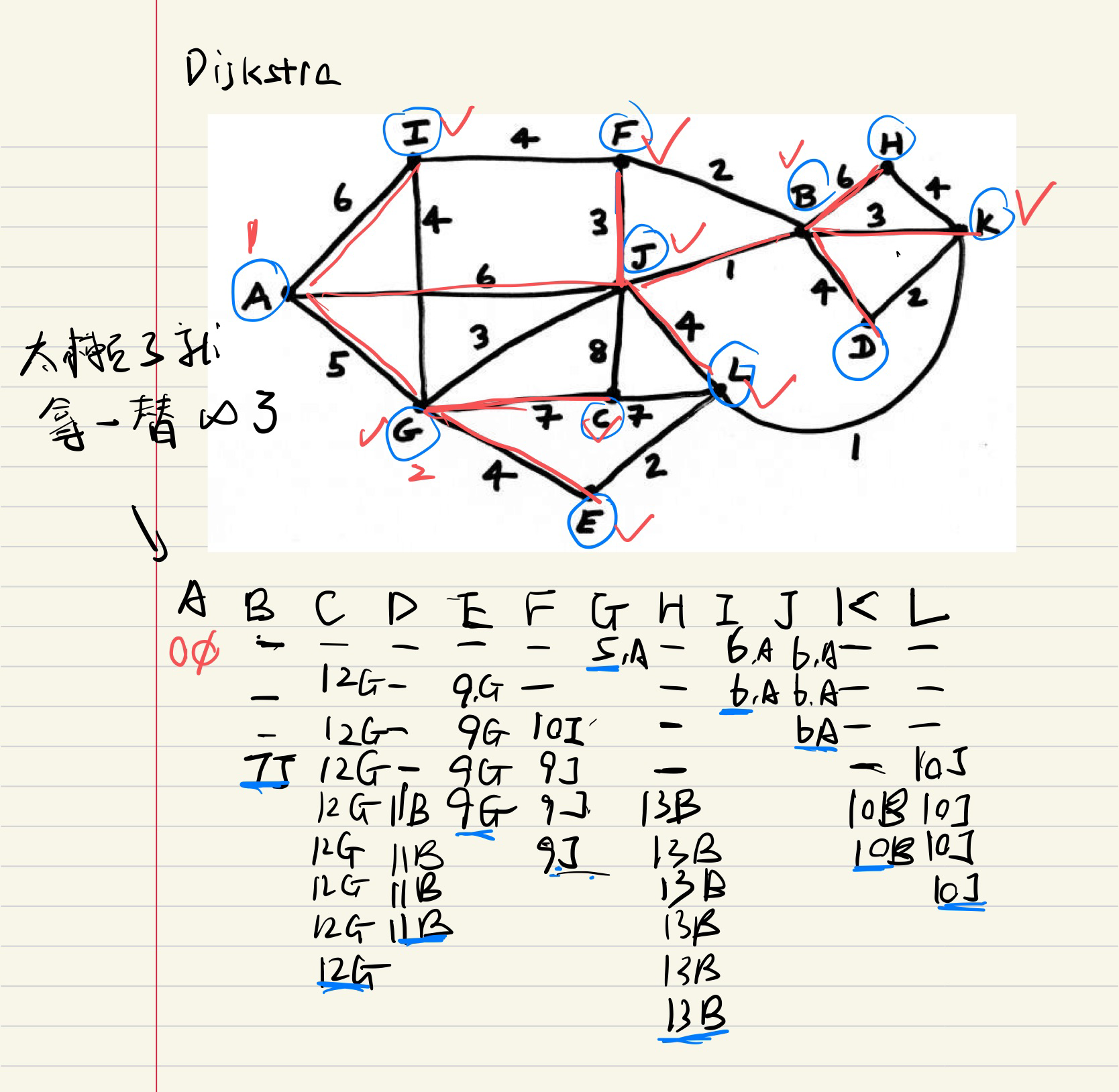
標答
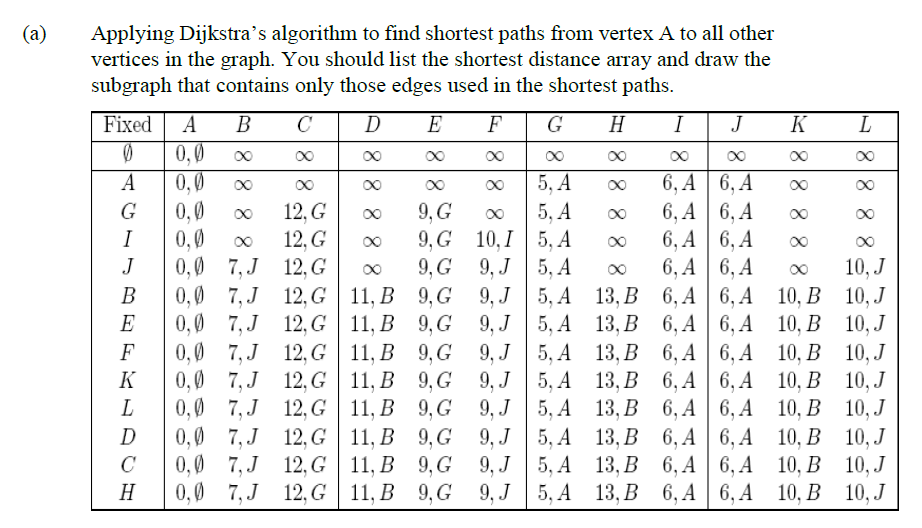
Bellman-Ford暫時沒有例題
Kruskal
從最短的邊開始選逐漸選到大邊

我自己做的
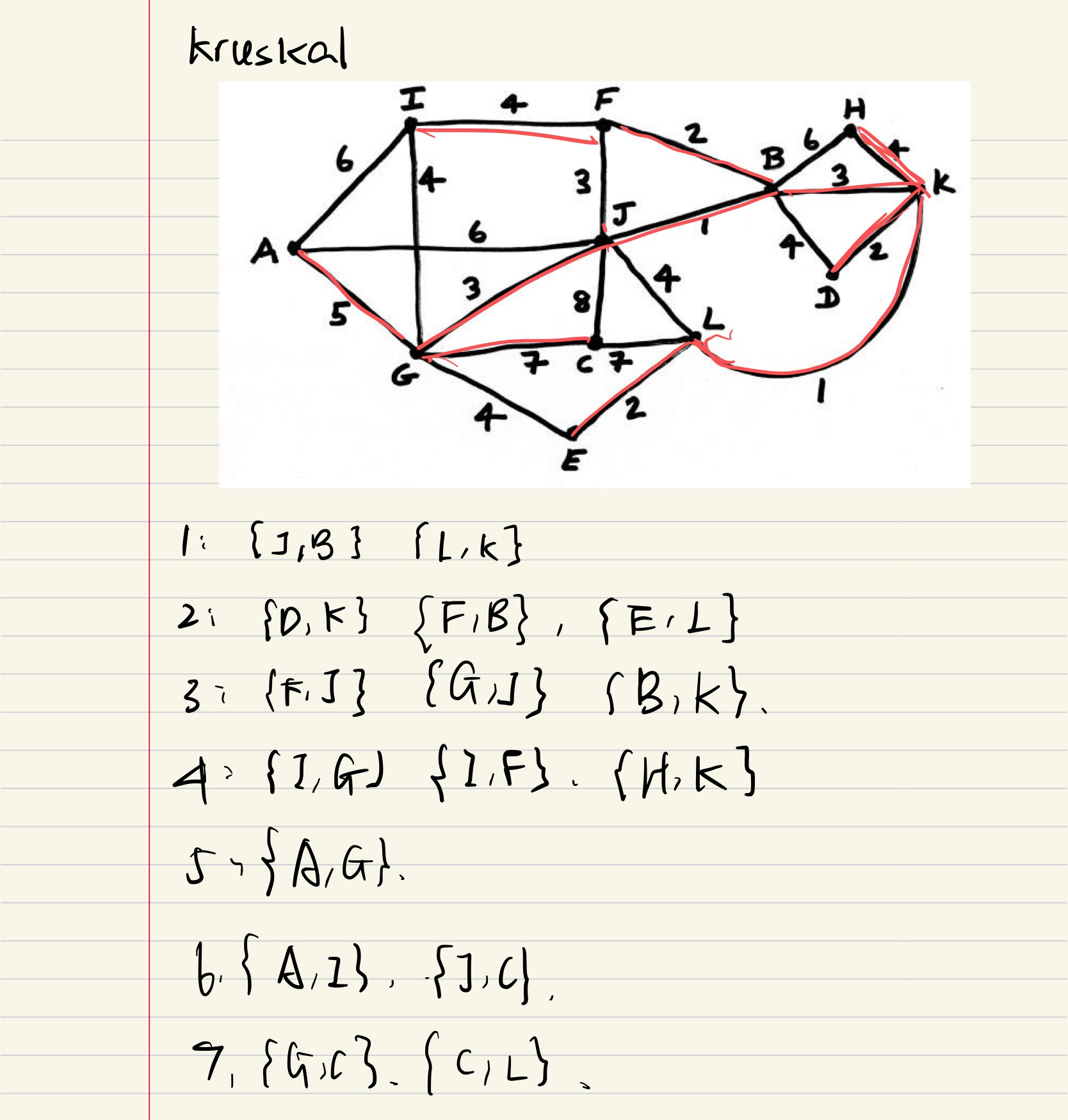
標答

Prim’s algorithm 找最小生成樹
1.選取權值最小邊的其中一個頂點作為起始點。
2.找到離當前頂點權值最小的邊,并記錄該頂點為已選擇。
3.重復第二步,直到找到所有頂點,就找到了圖的最小生成樹。
e.g1

自己寫的
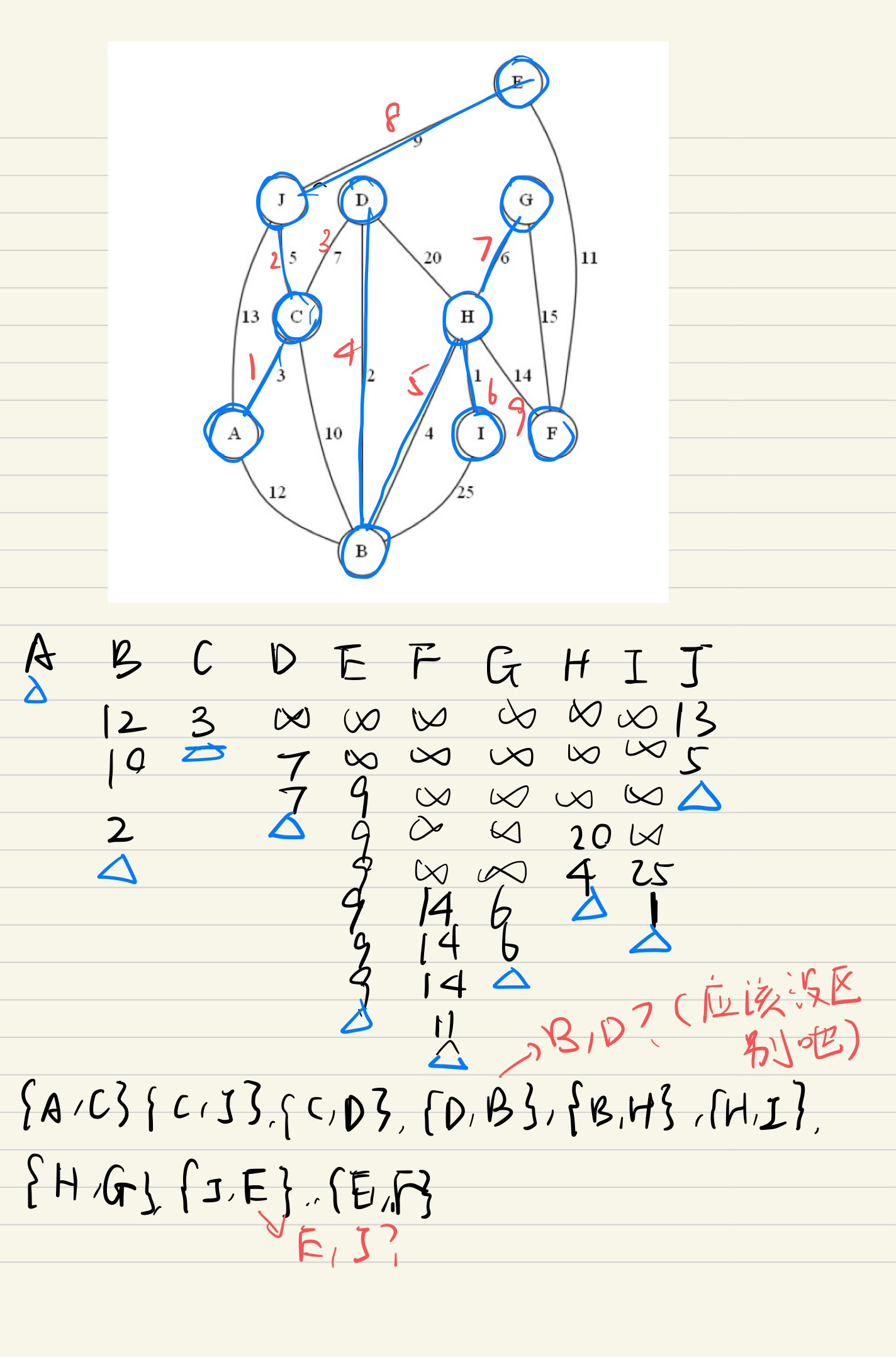
標答

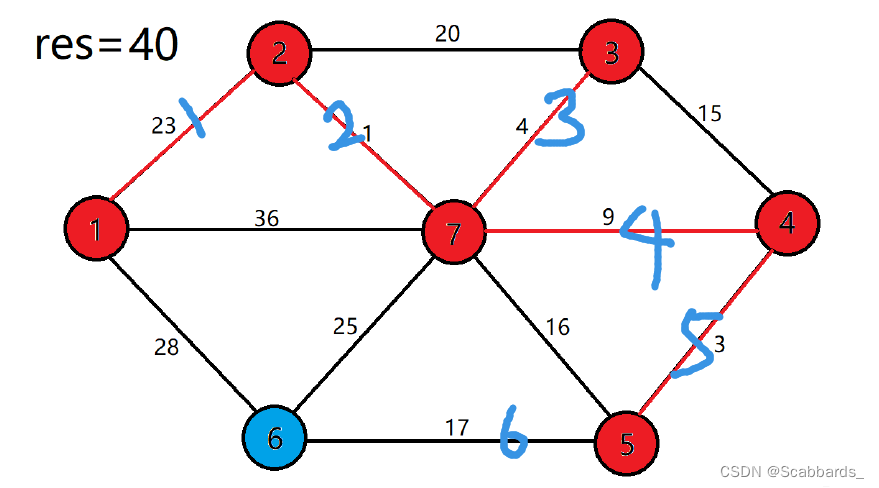
e.g2
?

e.g3
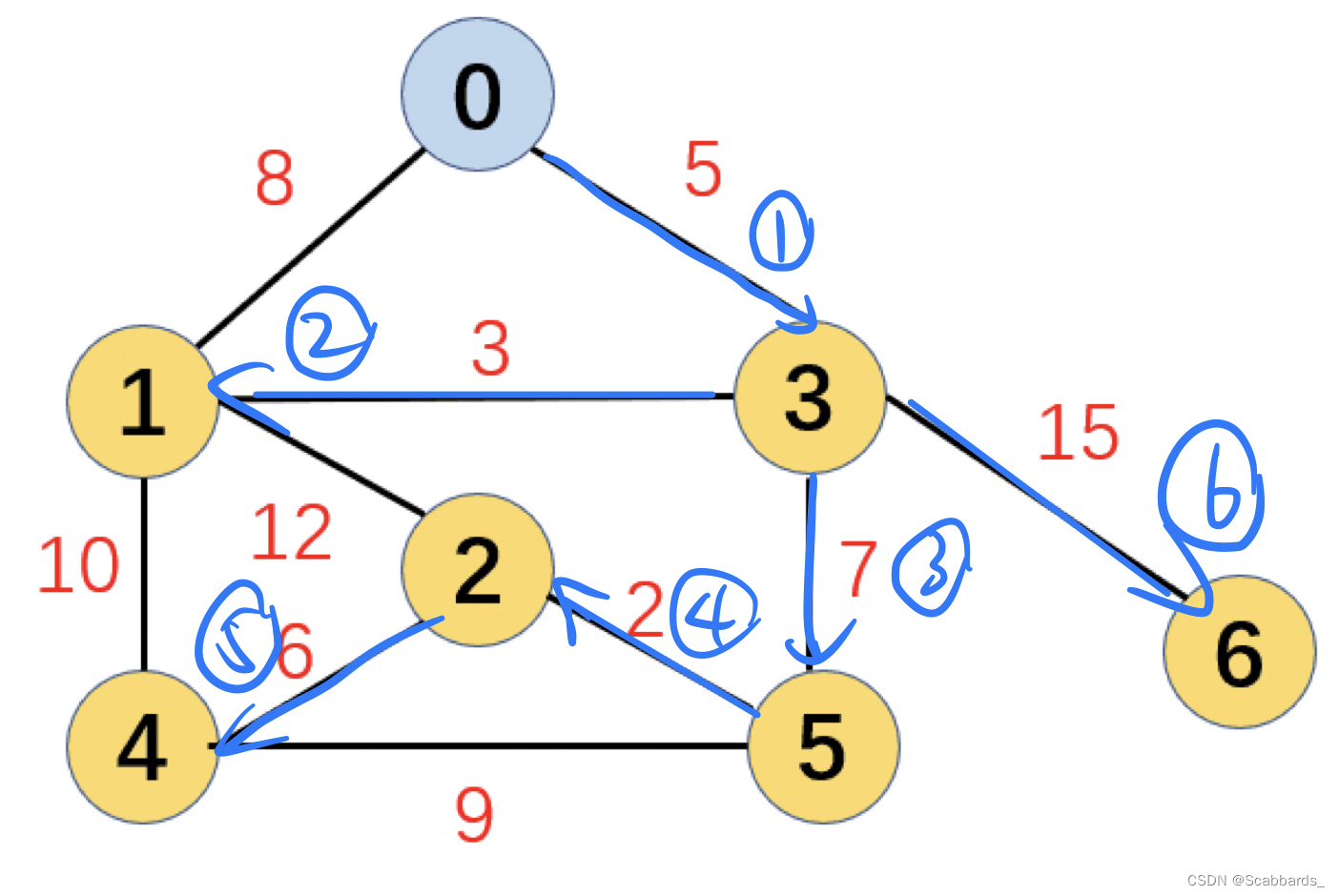
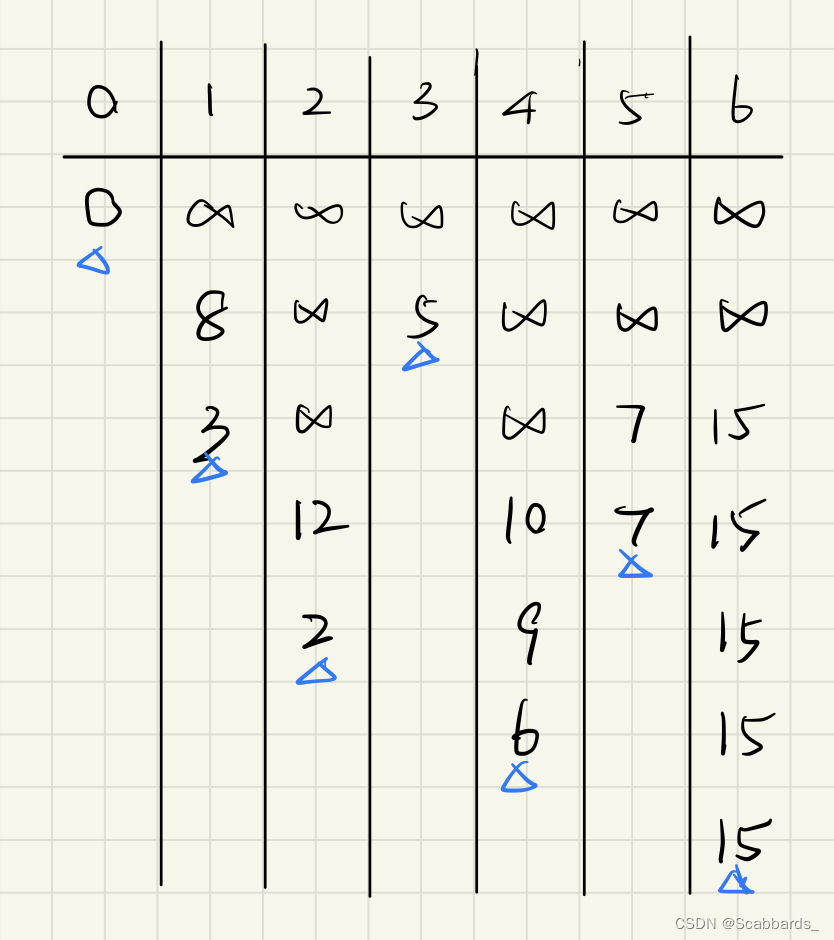
?BFS 定理證明
要是考試考這種證明我直接表演一個暴斃!

sol


Lec11 Flow 流
-
增廣路徑(Augmenting Path):
從起點s到t的簡單路徑,其中不能有回路 -
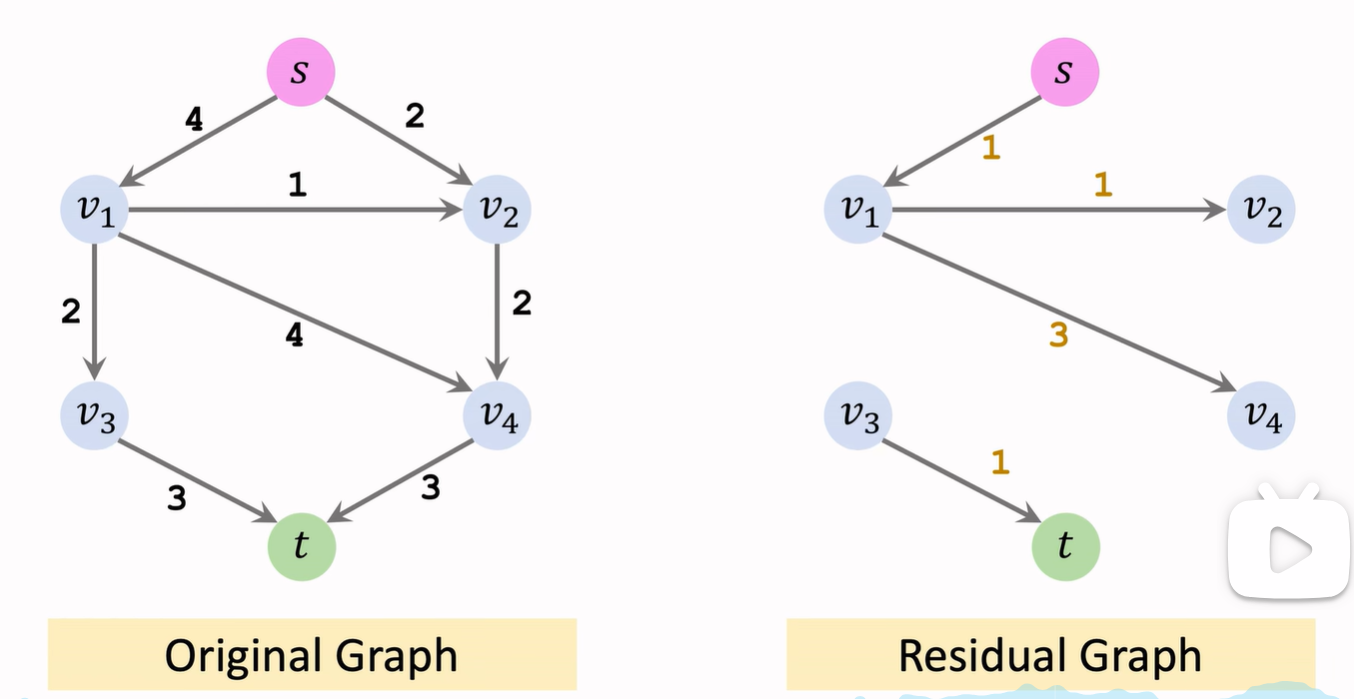
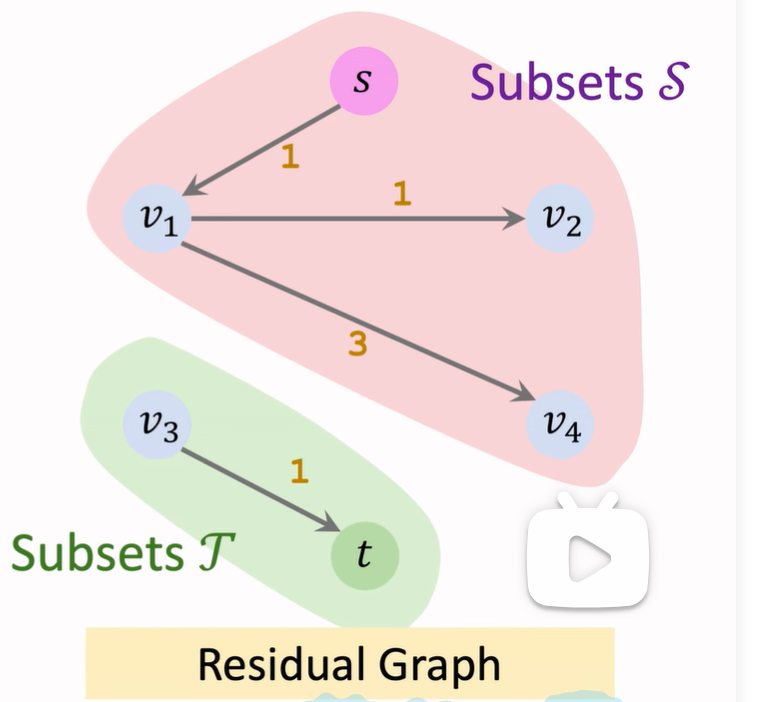
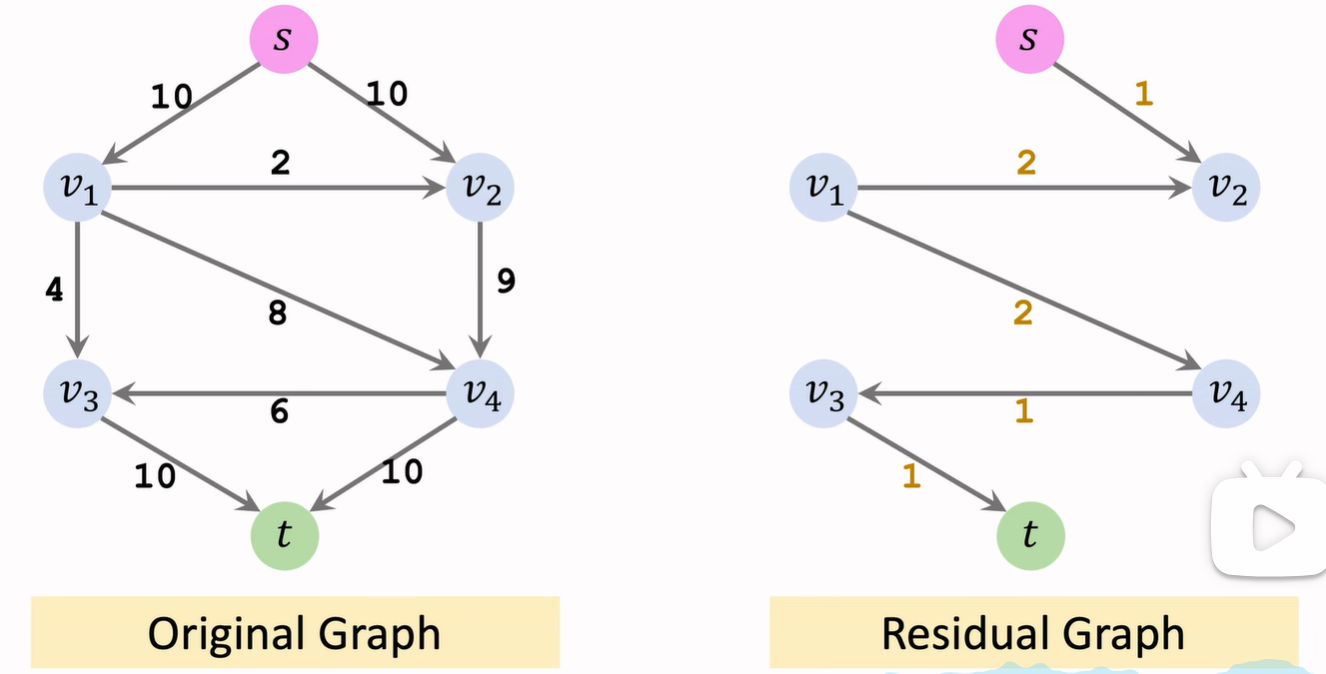
剩余網絡(Residual Network):
- 剩余網絡是在一個流網絡中,根據當前流量情況所生成的一個新的網絡。這個網絡中的邊表示原網絡中的邊上還能承載的額外流量。
- 對于每條邊,我們可以通過減去流量(已經通過的流量)來得到該邊的剩余容量。如果一條邊的剩余容量大于 0,則在剩余網絡中存在一條對應的邊,表示從該邊可以繼續傳送流量。
?Ford-Fulkerson Algorithm
1.先找到augmenting path
2. 添加backward path
e.g1
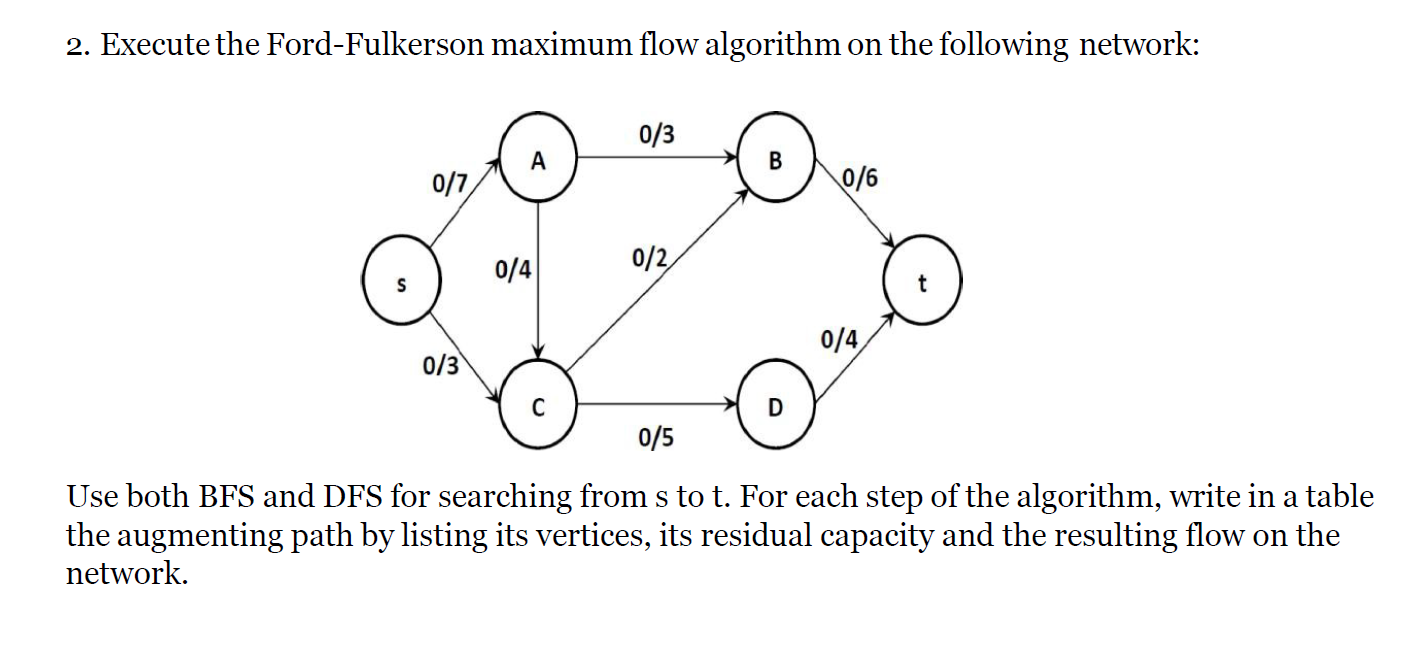
BFS 的逐層遍歷特性確保了每一層的節點在下一層的節點訪問前都被訪問
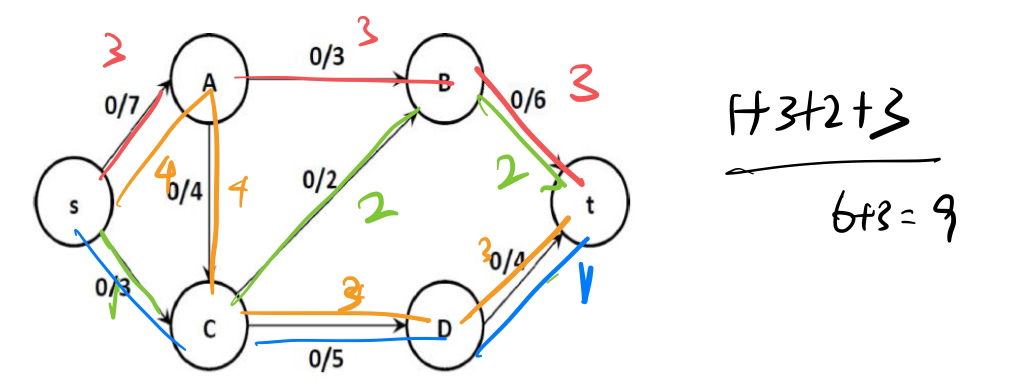

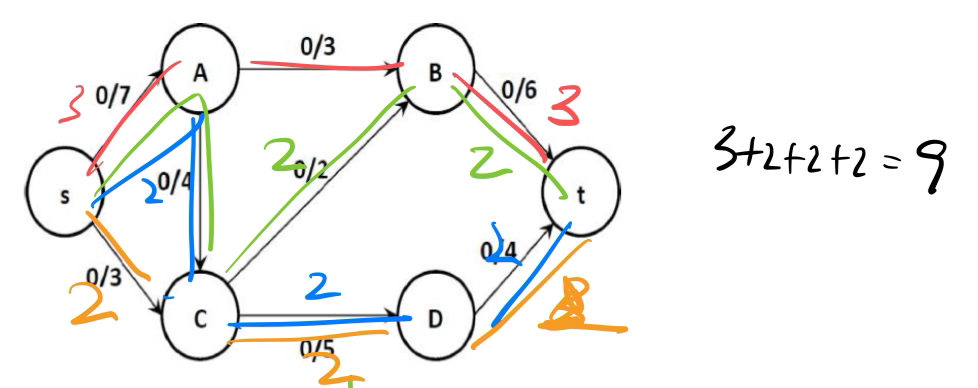

e.g2*


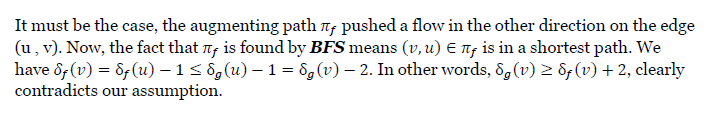
?e.g3
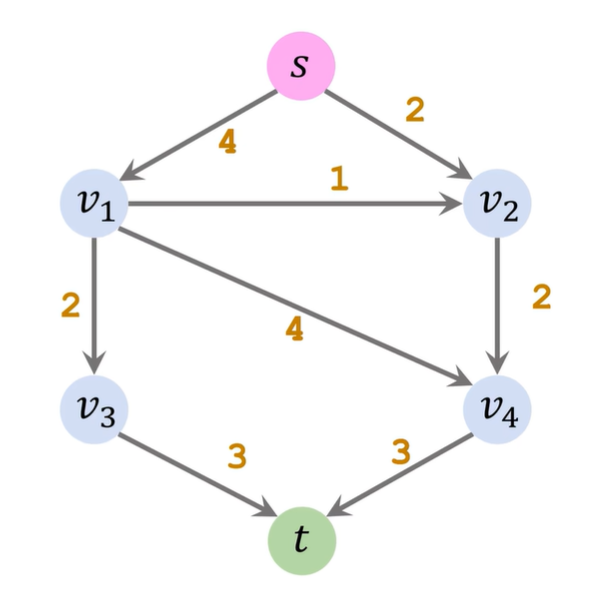

e.g4
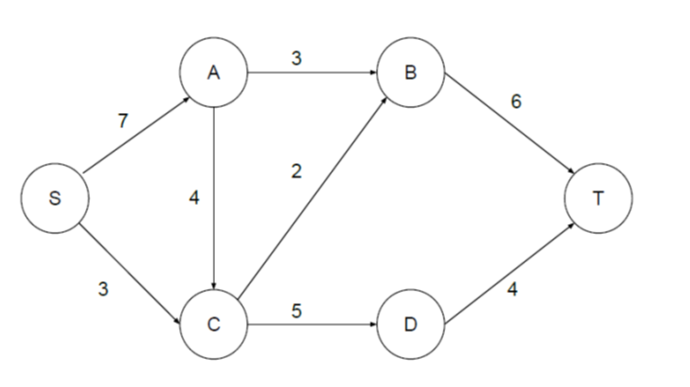
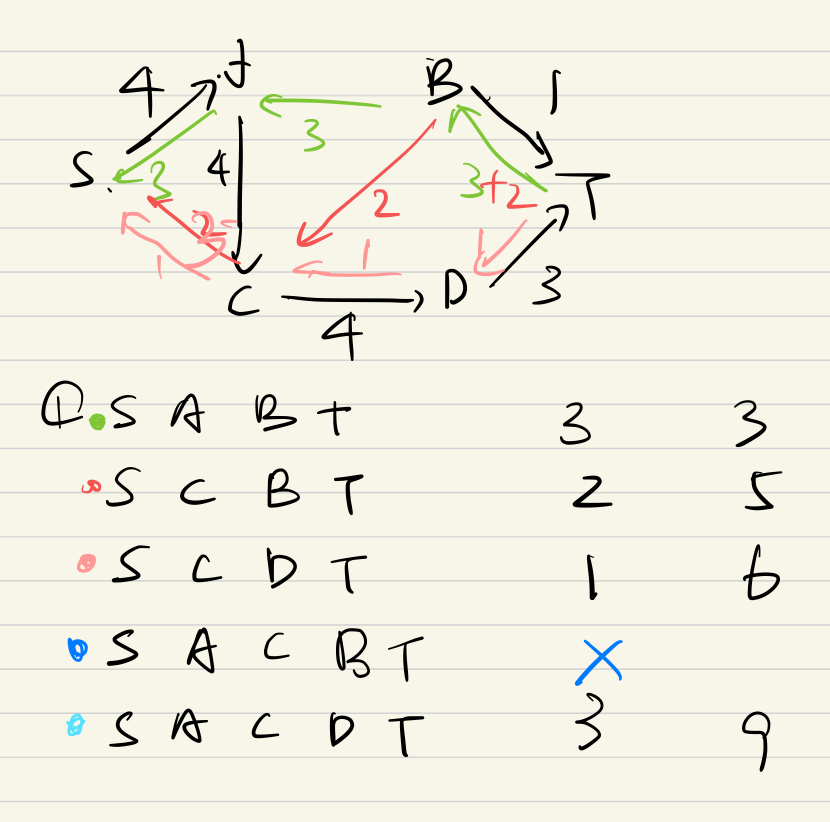
?
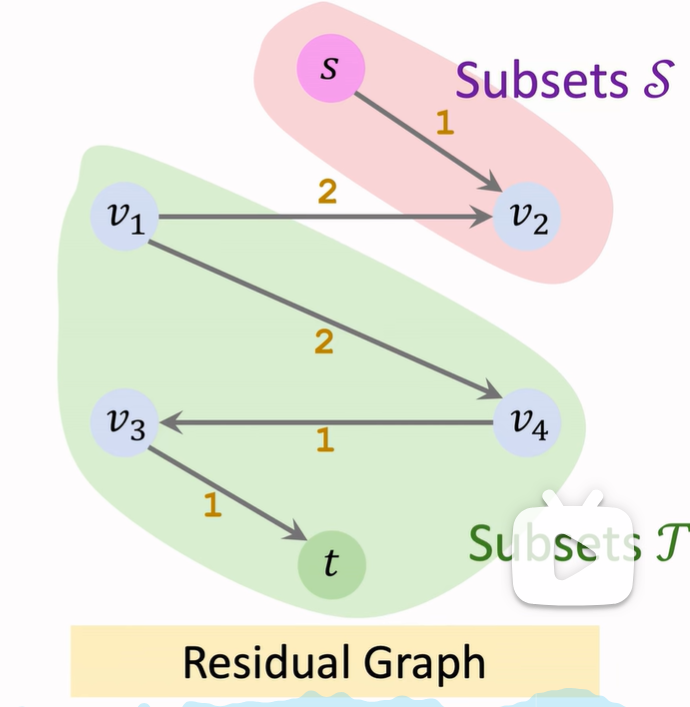
Min-cut
13-5: 最小割 Min-Cut_嗶哩嗶哩_bilibili
把原有集合分割成兩個部分,Min cut是讓總割斷的水管最小,讓水無法流往終點
注意,最小割不唯一
最大流最小割問題:最大流的流量等于最小割的容量

Lec13 Modular-Arithmetic
感覺Lec13和Lec14都能看這個我們的《密碼學的數學基礎》到底都介紹哪些內容,難不難_嗶哩嗶哩_bilibili
首先有個很重要的概念 x(mod y) 這種形式表示的是x除以y得到的余數?
Euclidean algorithm
這個方法也叫輾轉相除法,用來計算兩個數的最大公因數。
歐幾里得演算法(輾轉相除法)_嗶哩嗶哩_bilibili?這個講的很好的
拿大數/小數直到沒有余數為止
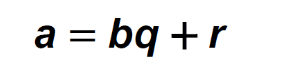
e.g1
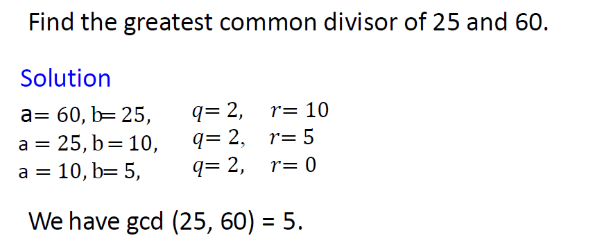
e.g2
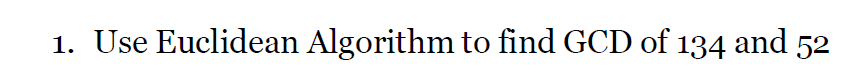

Extend Euclidean 拓展歐幾里得/廣義歐幾里得
用歐幾里得計算中每一步的出來的余數和商,用于計算sa +tb = gcd(a,b)中的s和t

r = a - c*b,然后通過前面的式子把a和b換掉
e.g1
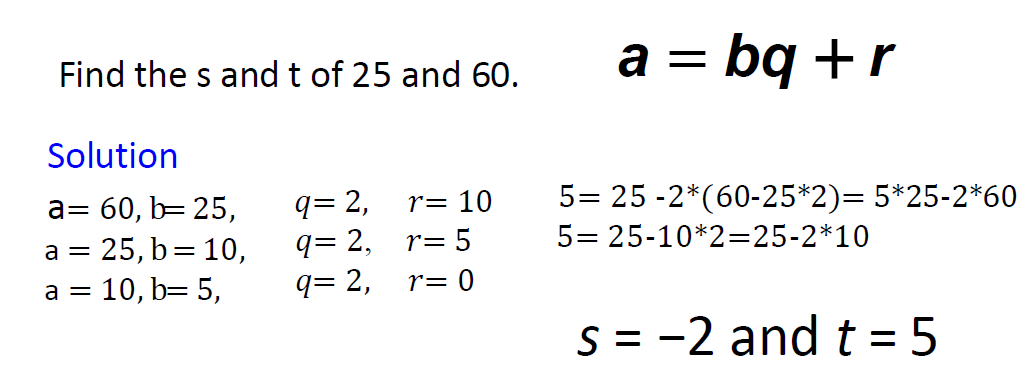
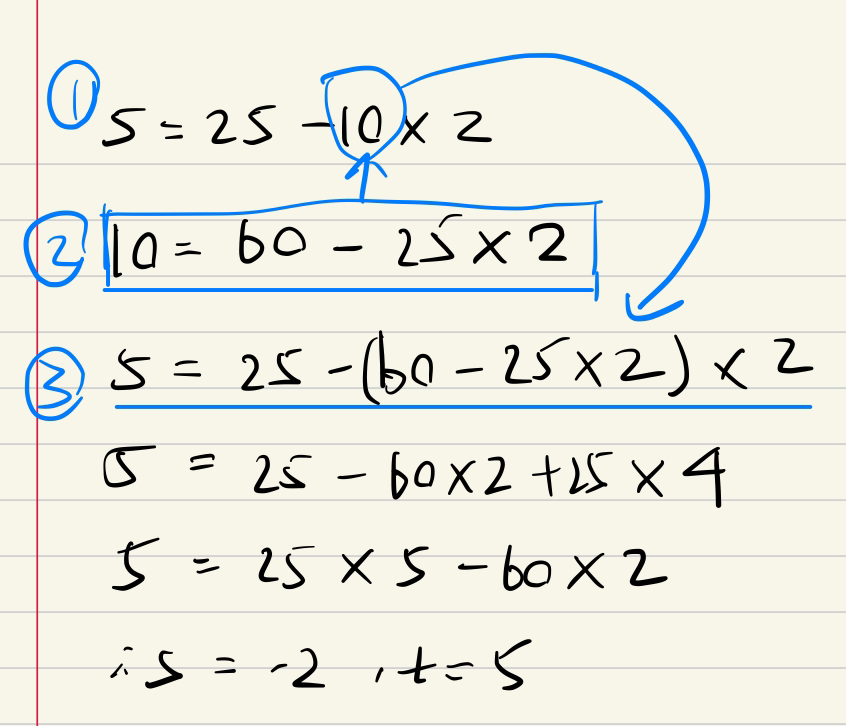
e.g2
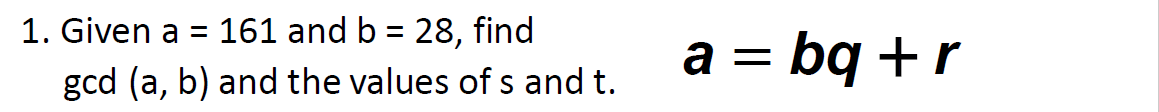
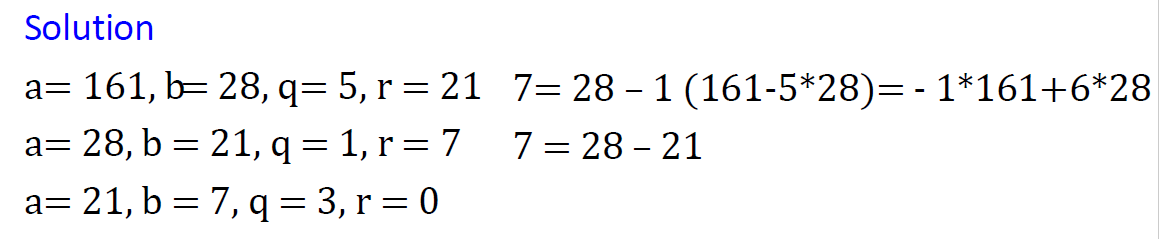
e.g3
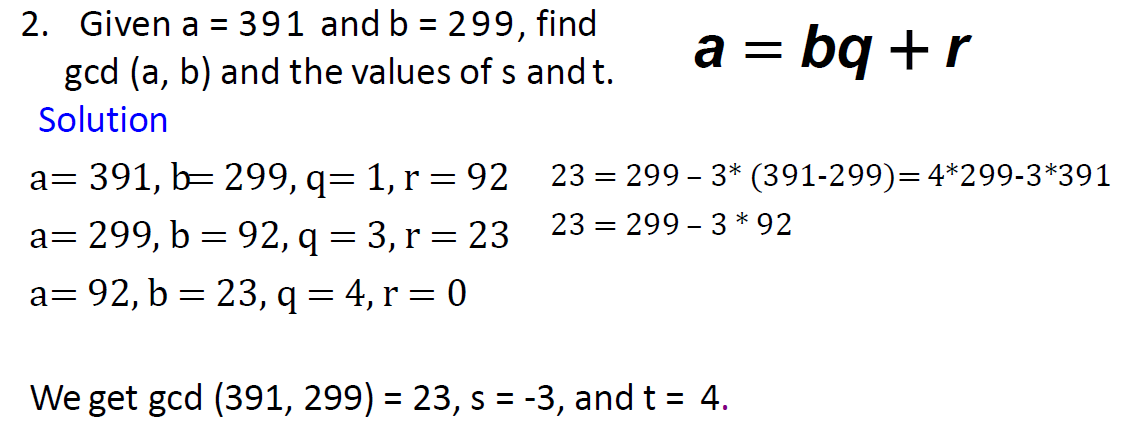
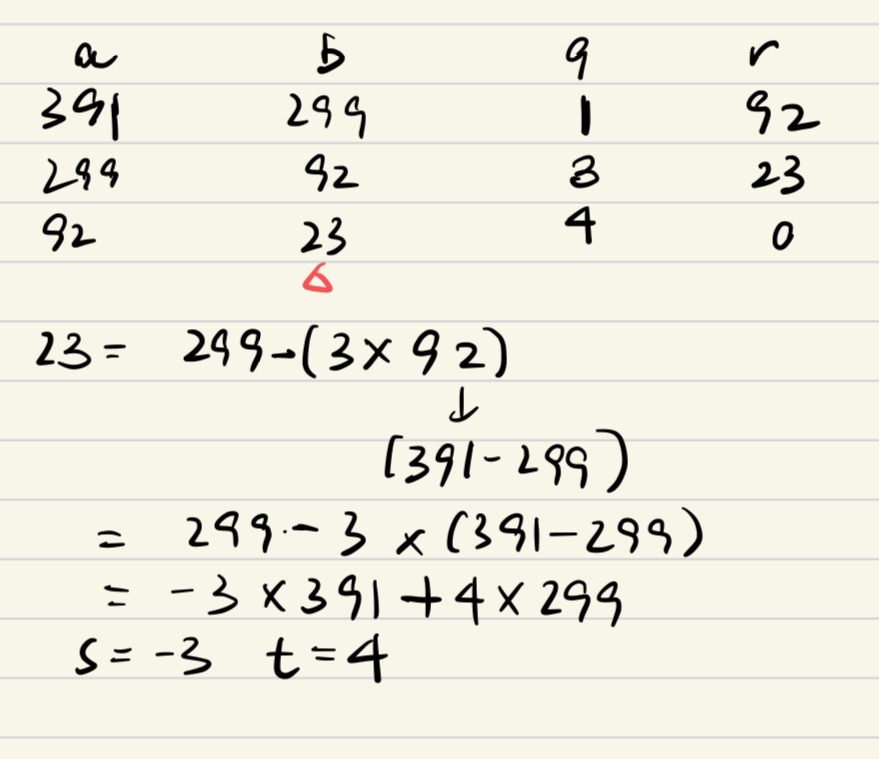
e.g4

我做的

標答(寫的好復雜噢)

Multiplicative Inverse 乘法逆元
乘法逆元在數論和抽象代數中是一個重要的概念,特別是在模運算(模算術)中有廣泛應用。給定一個整數 a和一個模數 m,如果存在一個整數 x使得
a ? x?≡ 1(mod m)
怎么找b在a乘法逆元:
1)先找到as + bt = 1 中的s和t(用拓展歐幾里得)
所以ab互質是充要條件,充要條件哈
2)t可能得到一個負數,但是可以通過? t?≡ u(mod m)
這個u就是最終答案
e.g1


e.g2?
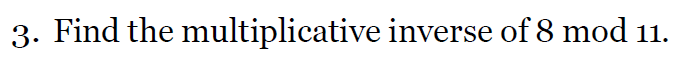

標答

Liner congruence
![]()
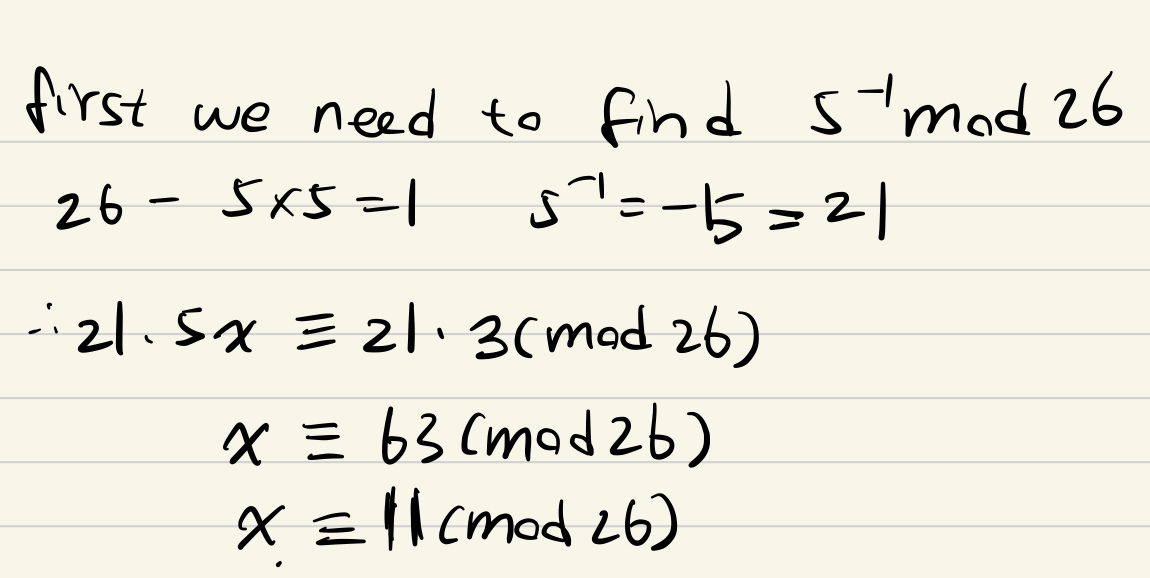
模運算的性質
?
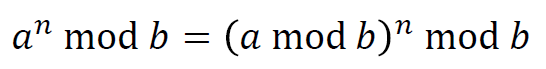
?e.g1**
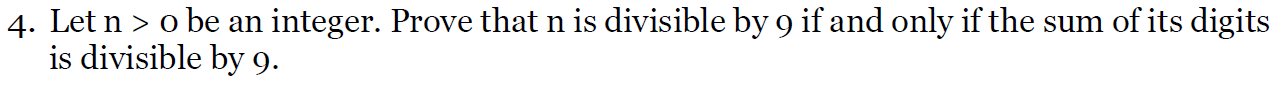
我自己寫的
老師標答
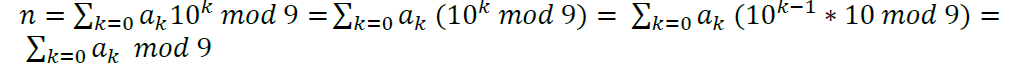

e.g2**
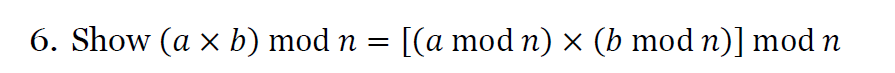
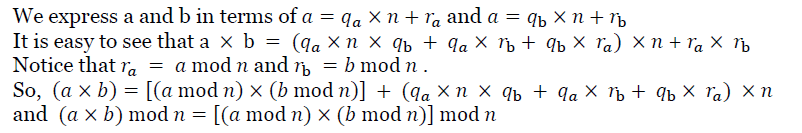
Fast Modular Exponentiation**

從前往后加
e.g1
![]()
?彼陽的ppt寫的變來變去的搞得我整了老半天,就不放老師ppt上的了,變你🐎呢推了我一個小時結果發現原來很簡單

Euler's Theorem
?是一個數學函數,用來計算小于等于某個正整數 n?的正整數中,與 n?互質的數的個數

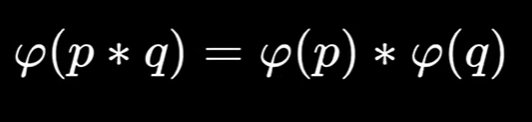


這里p是質數↑
e.g1
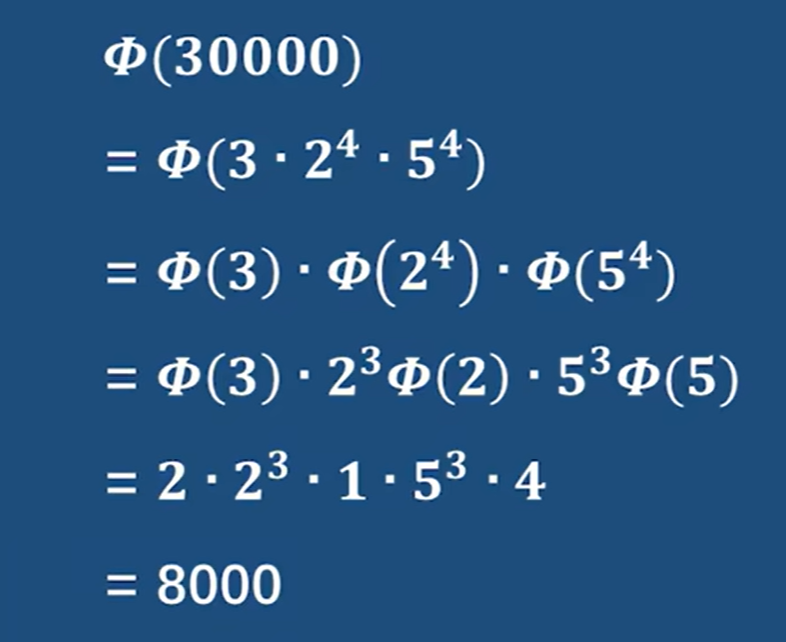
?
e.g2?
這題是乘法逆元和歐拉定理的綜合考察

sol

費馬小定理********
e.g1


RSA 非對稱加密
【RSA加密算法】| RSA加密過程詳解 | 公鑰加密| 密碼學| 信息安全|_嗶哩嗶哩_bilibili
public modulus(公鑰模數),是pq的乘積
很好的視頻,使我的大腦旋轉
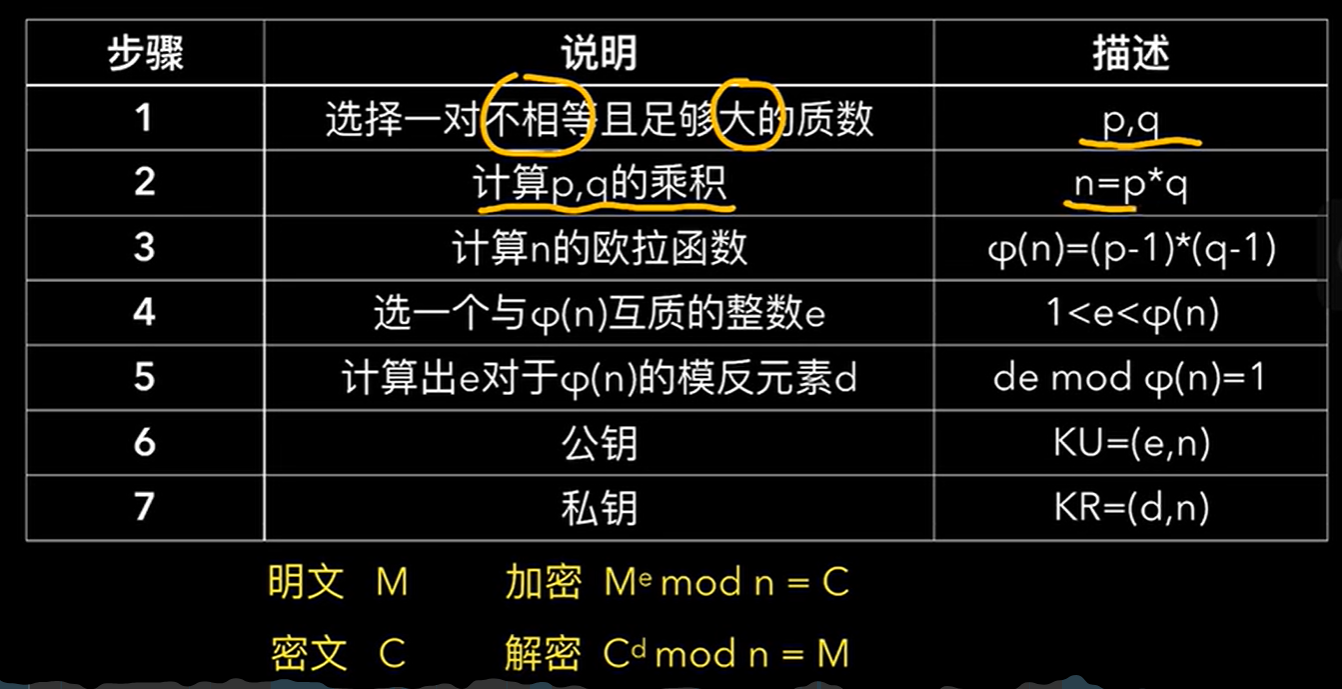
e.g1
e=3和p=17,q=23 是公鑰,求私鑰d
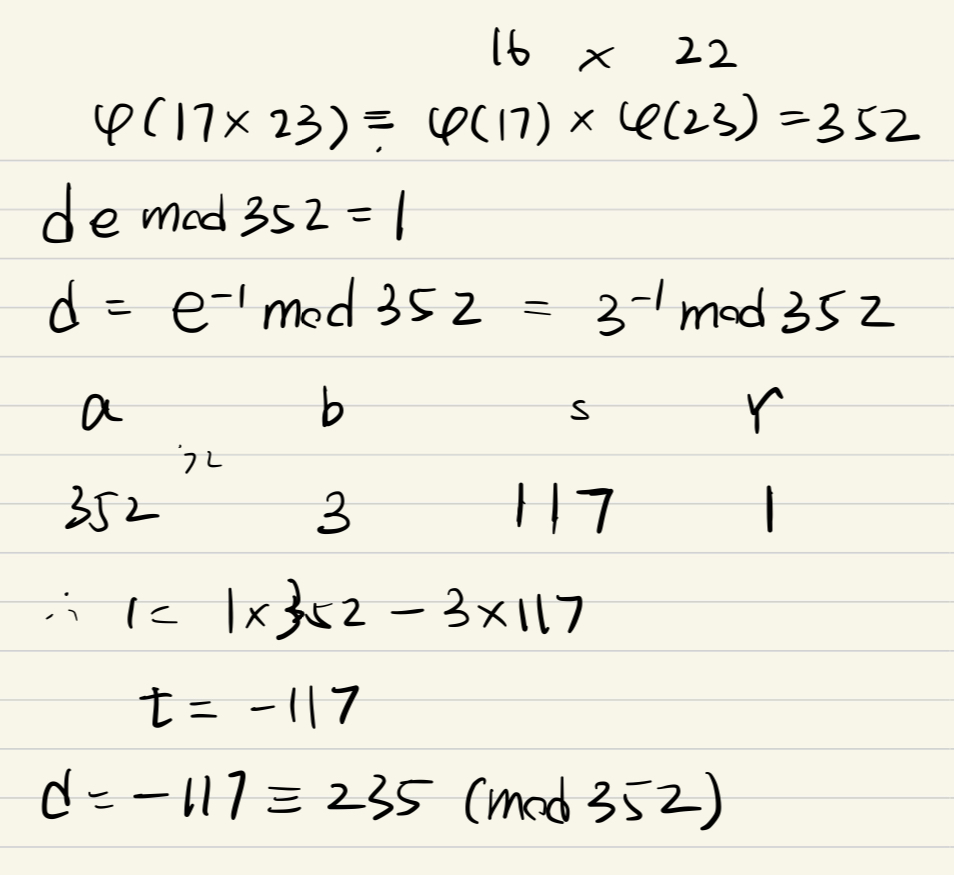
e.g2


老師標答
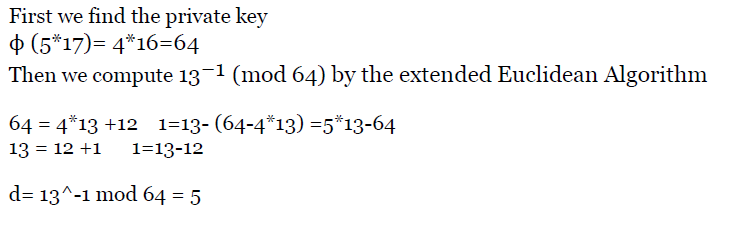

e.g3?
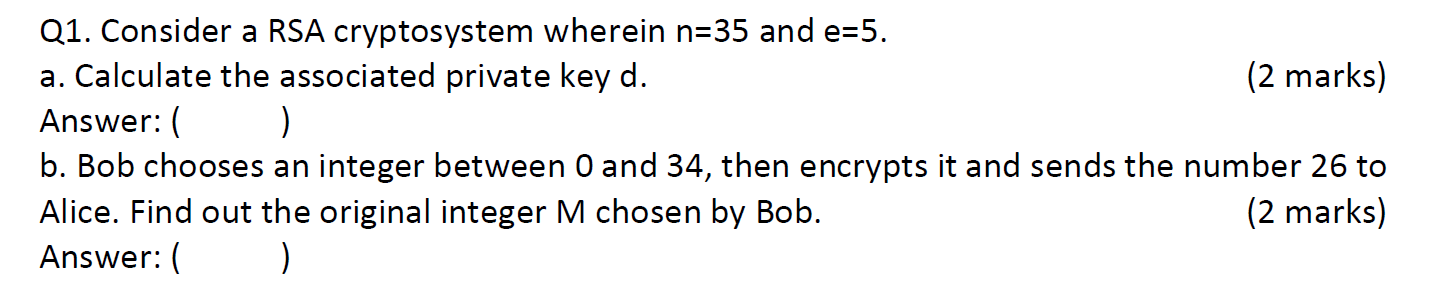

e.g4





Lec15 P,NP
期末復習的時候看到這個老師的視頻,醍醐灌頂了屬于是13.1 NP問題概述_嗶哩嗶哩_bilibili
劉老師,你學學人家
P: P類問題是指可以在多項式時間內(即時間復雜度為多項式函數的時間內)解決的問題。
NP:NP類問題是指能夠在多項式時間內驗證其解的問題。即使找到一個解可能很難,但一旦有了一個解,驗證其正確性可以在多項式時間內完成。因為P類問題能在多項式時間內驗證,所以P問題是NP問題,但是NP問題不一定是P問題
最優化問題(Optimization)轉化成判定性問題
NP-complete: NP中最難的問題,所有NP都可以規約(reducibility,實例對應,輸出一致,傳遞)到NPC問題,是NP-hard的子集
NP-hard: 多項式時間內不一定能驗證
SAT
中文名叫做合取范式CNF的可滿足性問題SAT,是NPC問題
3-SAT
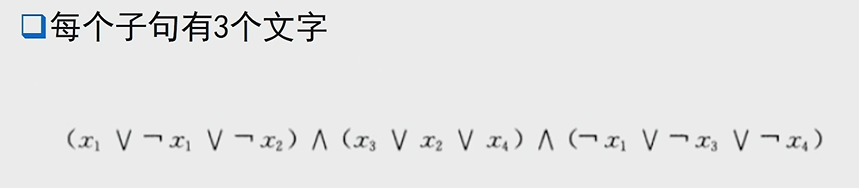

注意,2-SAT是P問題,3-SAT是NPC


e.g1

很好我也不會證,于是請教了萬能的chatgpt
標答
![]()
e.g2 3-SAT規約
這道題是把一個四合取范式規約成一個3CNF

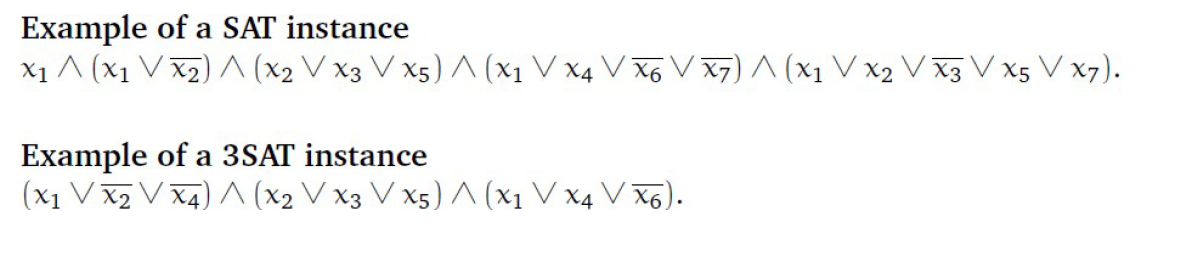
sol

e.g3
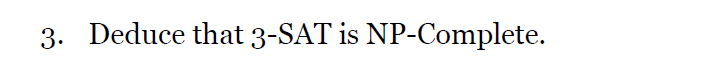

e.g4
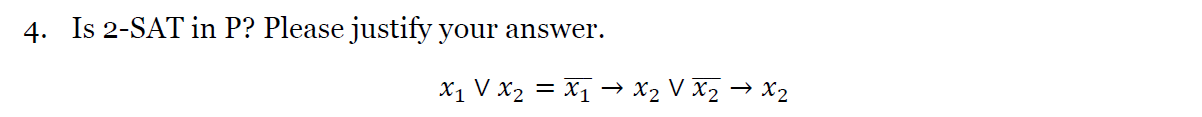
Yes,
公式可滿足
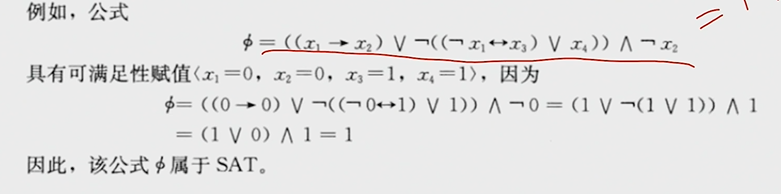
step1. 證明是個np問題

2.可滿足性
3. 一致性
e.g5


頂點問題

?Hamitonian cycle?



綜合題
?e.g1
![]()
![]()
![]()
![]()
e.g2
?


e.g3




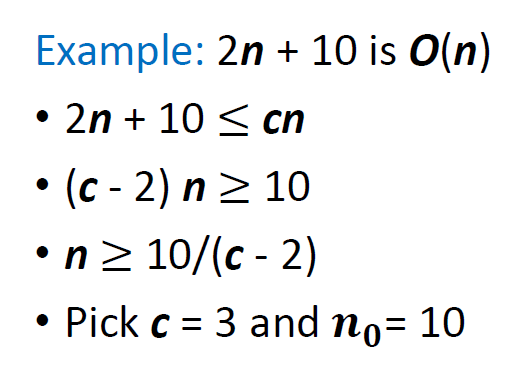
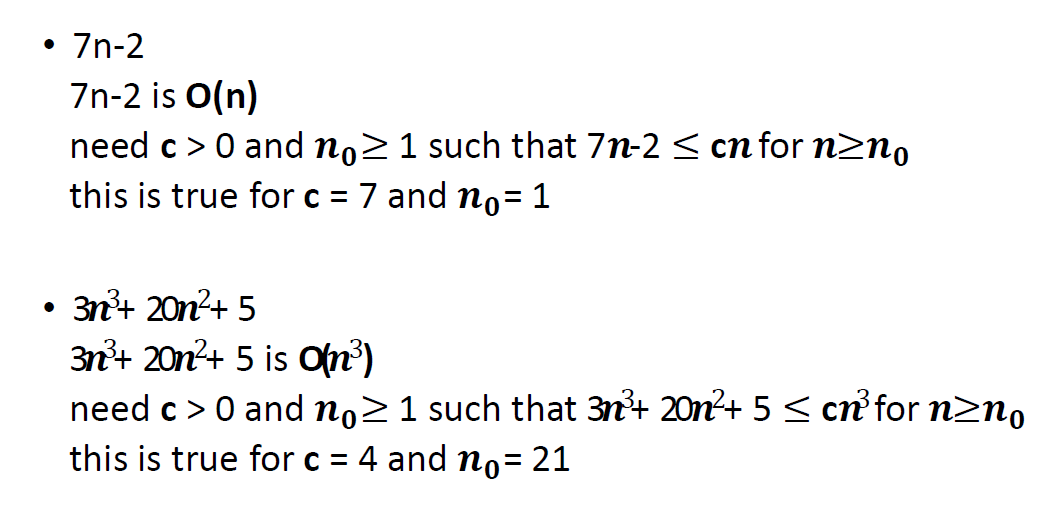
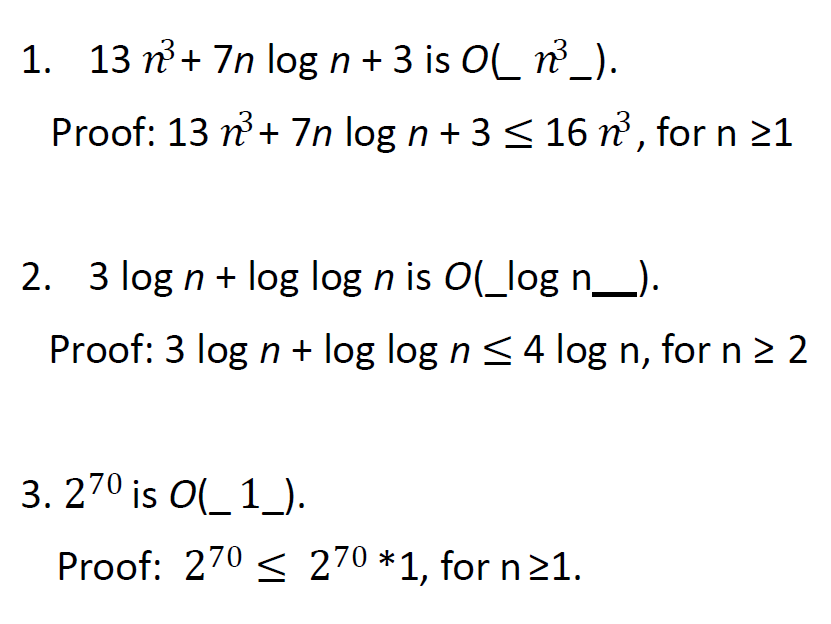

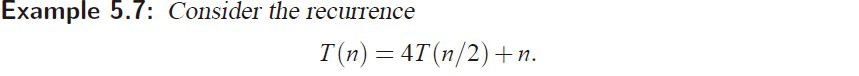

)





,sizeof和strlen的數組計算以及指針運算筆試難題詳解)







 Object Pascal 學習筆記---第14章泛型第2節(Object Pascal中的泛型))




