個人主頁? ? :敲上癮-CSDN博客 二叉樹介紹:二叉樹(詳解)-CSDN博客
目錄
一、二叉樹的創建
二、二叉樹的遍歷
1.前序遍歷
2.中序遍歷
3.后序遍歷
4.層序遍歷
三、相關計算
1.總節點個數計算
2.葉子節點個數計算
3.深度計算
一、二叉樹的創建
????????關于二叉樹的創建和遍歷我們考慮用遞歸來實現。
????????我們通過前序遍歷的數組"ABD##E#H##CF##G##" 來創建數組,其中 '#' 相當于空指針。
頭文件的聲明:
typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (*pi == n)return NULL;int val = a[(*pi)++];if (val == '#')return NULL;BTNode* root = (BTNode*)malloc(sizeof(BTNode));assert(root);root->_data = val;root->_left = BinaryTreeCreate(a, n, pi);root->_right = BinaryTreeCreate(a, n, pi);return root;
}二、二叉樹的遍歷
????????學習二叉樹結構,最簡單的方式就是遍歷。所謂二叉樹遍歷(Traversal)是按照某種特定的規則,依次對二叉樹中的結點進行相應的操作,并且每個結點只操作一次。訪問結點所做的操作依賴于具體的應用問題。
????????遍歷是二叉樹上最重要的運算之一,也是二叉樹上進行其它運算的基礎。
按照規則,二叉樹的遍歷有:前序/中序/后序的遞歸結構遍歷:
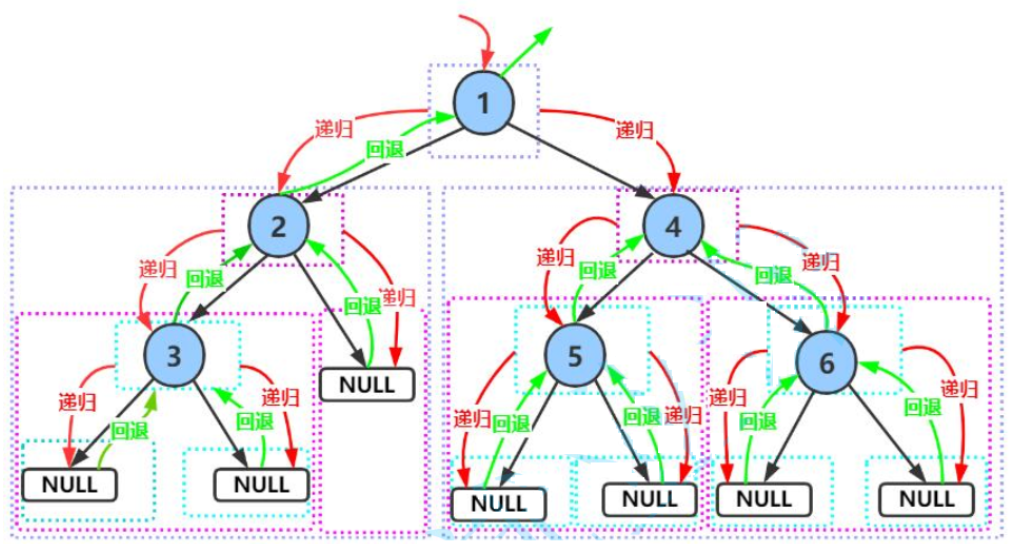
????????1. 前序遍歷(Preorder Traversal 亦稱先序遍歷)——訪問根結點的操作發生在遍歷其左右子樹之前。
????????2. 中序遍歷(Inorder Traversal)——訪問根結點的操作發生在遍歷其左右子樹之中(間)。
????????3. 后序遍歷(Postorder Traversal)——訪問根結點的操作發生在遍歷其左右子樹之后。
由于被訪問的結點必是某子樹的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解釋為根、根的左子樹和根的右子樹。NLR、LNR和LRN分別又稱為先根遍歷、中根遍歷和后根遍歷。
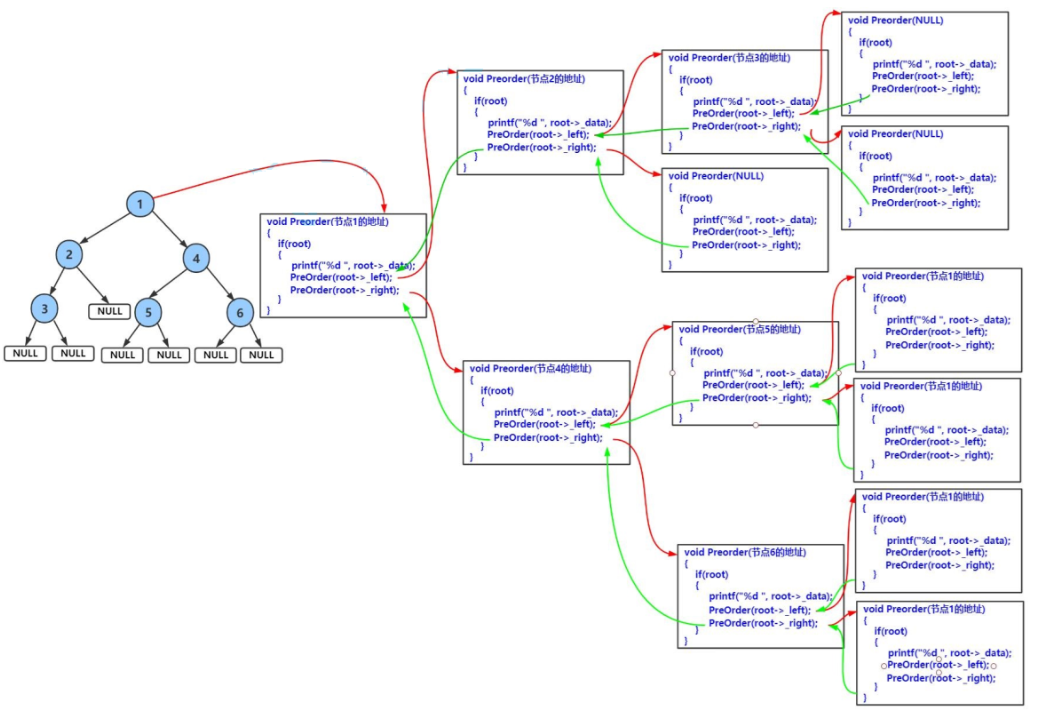
1.前序遍歷
void BinaryTreePrevOrder(BTNode* root)
{if (!root){printf("#");return;}printf("%c", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}
//或者這么寫:
void PrevOrder(BTNode* root)
{if (root){printf("%c", root->_data);PrevOrder(root->_left);PrevOrder(root->_right);}
}
2.中序遍歷
void BinaryTreeInOrder(BTNode* root)
{if (!root){printf("#");return;}BinaryTreeInOrder(root->_left);printf("%c", root->_data);BinaryTreeInOrder(root->_right);
}3.后序遍歷
void BinaryTreePostOrder(BTNode* root)
{if (!root){printf("#");return;}BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%c", root->_data);
}4.層序遍歷
????????層序遍歷是一層一層往下遍歷的,并不是單個方向深入,像以上三種遍歷都可以叫做深度優先遍歷,而層序遍歷也可以叫做廣度優先遍歷,它是不能用遞歸實現的,要實現它我們可以使用一個隊列結構,我們把根節點存入隊列然后對隊列進行操作,把根節點拿出來(Pop)然后把它的左孩子和右孩子依次取出放入隊列,然后再次從隊頭取到根節點重復操作,一次下去直到隊列為空,就能完成層序遍歷。如下:
void BinaryTreeLevelOrder(BTNode* root)
{if (!root)return;Queue pt;//需要構造出一個隊列結構,這里就不在展示QueueInit(&pt);QueuePush(&pt, root);while (!QueueEmpty(&pt)){BTNode* pf = QueueFront(&pt);if (pf)printf("%c", pf->_data);elseprintf("#");QueuePop(&pt);if (pf){QueuePush(&pt, pf->_left);QueuePush(&pt, pf->_right);}}
}三、相關計算
1.總節點個數計算
????????在計算節點個數的時候,初學著可能會想用一個全局變量,用以上任意方法遍歷并計數。這種方法是可行的但不太可靠。像這些二叉樹相關的計算我們大多數都可以考慮把它化為小問題去分析。如果是空樹的話就是0,如果不是空樹就是1+左樹的節點個數+右樹的節點個數,像這樣左樹又可以分為左樹和右樹去解決,可以不斷的把問題化小。如下:
int BinaryTreeSize(BTNode* root)
{if (!root)return 0;elsereturn BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}2.葉子節點個數計算
這個計算和上一個方法是相似的,不過我們得特別判斷以下是否為葉子節點。如下:
int BinaryTreeLeafSize(BTNode* root)
{if (!root)return 0;if (!root->_left && !root->_right)return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}3.深度計算
????????求一顆樹的深度可以化為就是左子樹的深度和右子樹中的最大深度,而左子樹又可以在化為更小的左右子樹的深度就如此遞推下去,直到遇到空樹才一次回歸(返回),這樣就把大問題化為小問題用遞歸實現。如下:
int BinaryTreeHeight(BTNode* root)
{if (!root)return 0;int v1=BinaryTreeHeight(root->_left);int v2 = BinaryTreeHeight(root->_right);return v1 > v2 ? v1 + 1 : v2 + 1;
}要注意一點的是千萬不要寫成下面的方式:?
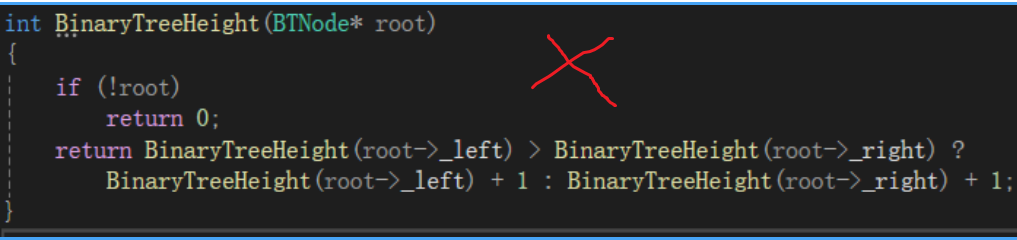
這樣會使一個函數內就有三個遞歸展開,效率會變得非常非常低。?





與dict協議(在線詞典))

)











