? ?純? ?干? ?貨~?
目錄
純干貨
1、L1 正則化(Lasso 正則化)
2、L2 正則化(嶺正則化)
3、彈性網絡正則化(Elastic Net 正則化)
4、Dropout 正則化(用于神經網絡)
5、貝葉斯Ridge和Lasso回歸
貝葉斯Ridge回歸
貝葉斯Lasso回歸
6、早停法(Ear
7、數據增強
?正則化是一種用于降低機器學習模型過擬合風險的技術。當模型過度擬合訓練數據時,它會在新樣本上表現不佳。所以為了解決這個問題,我們必須要引入正則化算法。
正則化通過在模型的損失函數中添加一個正則項(懲罰項)來實現。這個正則項通常基于模型參數的大小,以限制模型參數的數量或幅度。主要有兩種常見的正則化算法:L1正則化和L2正則化。
-
L1正則化(Lasso):L1正則化添加了模型參數的絕對值之和作為正則項。它傾向于使一些參數變為零,從而達到特征選擇的效果。所以,L1正則化可以用于自動選擇最重要的特征,并減少模型復雜度。
-
L2正則化(Ridge):L2正則化添加了模型參數的平方和作為正則項。它傾向于使所有參數都較小,但沒有明確地將某些參數設置為零。L2正則化對異常值更加魯棒,并且可以減少模型的過度依賴單個特征的情況。
正則化通過控制模型參數的大小來限制模型的復雜度,從而避免過擬合。在損失函數中引入正則項后,模型的優化目標變為最小化損失函數和正則項之和。
今天要探究的是這7各部分,大家請看~
-
L1 正則化
-
L2 正則化
-
彈性網絡正則化
-
Dropout 正則化
-
貝葉斯Ridge和Lasso回歸
-
早停法
-
數據增強
1、L1 正則化(Lasso 正則化)
L1正則化(也稱為Lasso正則化)是一種用于控制機器學習模型復雜度的技術。
通過向損失函數添加L1范數項來實現正則化,鼓勵模型產生稀疏權重,即將一些特征的權重調整為0。
公式:
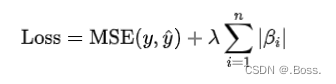
L1正則化在優化過程中有兩個關鍵特點:
1、由于正則化項中包含絕對值操作,導致損失函數不可導。因此,在求解最小化損失函數時,需要使用其他方法(如坐標下降、梯度下降等)。
2、正則化項的存在促使部分特征的權重變為0,從而實現特征選擇和模型簡化。
咱們看一個簡單案例,使用了sklearn庫中的Lasso類來實現L1正則化的模型:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso# 生成示例數據
np.random.seed(42)
X = np.linspace(-5, 5, num=100).reshape(-1, 1)
y = 2 * X + np.random.normal(0, 1, size=(100, 1))# 創建Lasso模型對象
lasso = Lasso(alpha=0.1) # 設置alpha參數,控制正則化強度# 擬合數據
lasso.fit(X, y)# 繪制優化復雜圖形
fig, ax = plt.subplots()
ax.scatter(X, y, color="blue", label="Data")
ax.plot(X, lasso.predict(X), color="red", linewidth=2, label="L1 Regularization")# 在圖中繪制L1正則化項的等高線
beta_0 = np.linspace(-10, 10, 100)
beta_1 = np.linspace(-10, 10, 100)
B0, B1 = np.meshgrid(beta_0, beta_1)
Z = np.zeros_like(B0)
for i in range(len(beta_0)):for j in range(len(beta_1)):lasso.coef_ = np.array([B0[i,j], B1[i,j]])Z[i,j] = np.sum(np.abs(lasso.coef_))
ax.contour(B0, B1, Z, levels=20, colors="black", alpha=0.5)ax.set_xlabel("X")
ax.set_ylabel("y")
ax.set_title("L1 Regularization with Contour Plot")
ax.legend()
plt.show()除了繪制原始數據點和經過L1正則化的擬合線外,我們還使用等高線圖形展示了L1正則化項。通過等高線圖,可以更加直觀地看到正則化項對權重的影響,以及如何促使模型產生稀疏權重。
2、L2 正則化(嶺正則化)
L2正則化(也稱為嶺正則化)是一種用于控制機器學習模型復雜度的技術。
它通過向損失函數添加L2范數項來實現正則化,鼓勵模型產生平滑權重,即將特征的權重調整為較小的值。
公式:
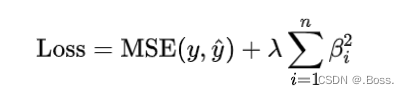
L2正則化在優化過程中的2個關鍵特點:
1、正則化項中包含平方操作,使得損失函數可導。因此,在求解最小化損失函數時,可以使用常見的梯度下降等優化算法。
2、正則化項的存在使得特征權重趨向于較小的值,從而避免了過擬合問題。
先看一個案例,使用sklearn庫中的Ridge類來實現L2正則化的模型:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge# 生成示例數據
np.random.seed(42)
X = np.linspace(-5, 5, num=100).reshape(-1, 1)
y = 2 * X + np.random.normal(0, 1, size=(100, 1))# 創建Ridge模型對象
ridge = Ridge(alpha=0.1) # 設置alpha參數,控制正則化強度# 擬合數據
ridge.fit(X, y)# 繪制優化復雜圖形
fig, ax = plt.subplots()
ax.scatter(X, y, color="blue", label="Data")
ax.plot(X, ridge.predict(X), color="red", linewidth=2, label="L2 Regularization")# 在圖中繪制L2正則化項的等高線
beta_0 = np.linspace(-10, 10, 100)
beta_1 = np.linspace(-10, 10, 100)
B0, B1 = np.meshgrid(beta_0, beta_1)
Z = np.zeros_like(B0)
for i in range(len(beta_0)):for j in range(len(beta_1)):ridge.coef_ = np.array([B0[i,j], B1[i,j]])Z[i,j] = np.sum(ridge.coef_ ** 2)
ax.contour(B0, B1, Z, levels=20, colors="black", alpha=0.5)ax.set_xlabel("X")
ax.set_ylabel("y")
ax.set_title("L2 Regularization with Contour Plot")
ax.legend()
plt.show()除了繪制原始數據點和經過L2正則化的擬合線外,我們還使用等高線圖形展示了L2正則化項。通過等高線圖,可以更加直觀地看到正則化項對權重的影響,以及如何促使模型產生平滑權重。
3、彈性網絡正則化(Elastic Net 正則化)
彈性網絡正則化是一種用于線性回歸模型的正則化方法,結合了L1和L2正則化的特點。
可以在具有大量特征的數據集上處理多重共線性問題,并選擇相關特征。
彈性網絡正則化通過加權L1范數和L2范數來控制正則化項的大小。L1范數在某些情況下會產生稀疏解(即部分系數為零),而L2范數鼓勵系數的平滑性。
因此,彈性網絡正則化可以綜合利用L1和L2正則化的優勢。
彈性網絡正則化的損失函數可以表示為:
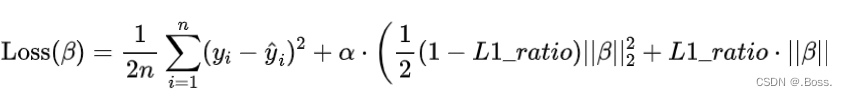
下面是使用Python的scikit-learn庫來擬合彈性網絡回歸模型:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet# 生成一些樣本數據
np.random.seed(42)
n_samples = 100
X = np.linspace(-3, 3, n_samples)
y = 0.5 * X + np.random.normal(scale=0.5, size=n_samples)# 創建并擬合彈性網絡模型
enet = ElasticNet(alpha=0.5, l1_ratio=0.7)
enet.fit(X.reshape(-1, 1), y)# 繪制原始數據和擬合曲線
plt.scatter(X, y, color='b', label='Original data')
plt.plot(X, enet.predict(X.reshape(-1, 1)), color='r', linewidth=2, label='Elastic Net')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Elastic Net Regression')
plt.show()代碼中生成了一些具有噪聲的樣本數據,并使用彈性網絡模型進行擬合。
通過繪制原始數據和擬合曲線,可以更好地理解彈性網絡正則化在回歸問題中的應用。
案例中只是一個簡單的示例,實際使用時需要調整參數和改進模型以適應具體問題。
4、Dropout 正則化(用于神經網絡)
Dropout 正則化是一種用于神經網絡的正則化方法。
通過在訓練過程中隨機將一部分神經元的輸出設置為零,從而減少神經網絡中的過擬合現象。
Dropout 正則化可以提高模型的泛化能力,并防止神經元之間過度依賴。
Dropout 正則化的原理是,在訓練期間以概率??隨機地將一部分神經元的輸出設置為零,稱為“丟棄”。丟棄的方式是對每個神經元引入一個二進制的隨機變量?,取值為 0 或 1,表示該神經元是否被丟棄。在前向傳播和反向傳播過程中,丟棄的神經元及其連接會被忽略。
在訓練過程中,Dropout 正則化的損失函數可以表示為:
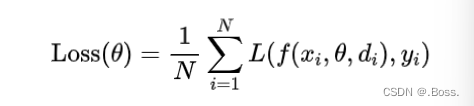
在測試階段,不再進行丟棄操作,而是將所有神經元的輸出乘以概率 P。通過這種方式,Dropout 正則化可以減少神經元之間的依賴性,提高模型的魯棒性。
下面使用Python的tensorflow庫來構建一個具有Dropout正則化的簡單神經網絡:
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf# 生成一些樣本數據
np.random.seed(42)
n_samples = 100
X = np.linspace(-3, 3, n_samples)
y = 0.5 * X + np.random.normal(scale=0.5, size=n_samples)# 構建神經網絡模型
model = tf.keras.models.Sequential([tf.keras.layers.Dense(16, activation='relu', input_shape=(1,)),tf.keras.layers.Dropout(0.5),tf.keras.layers.Dense(1)
])# 編譯和擬合模型
model.compile(optimizer='adam', loss='mean_squared_error')
model.fit(X, y, epochs=50, batch_size=16, verbose=0)# 繪制原始數據和擬合曲線
plt.scatter(X, y, color='b', label='Original data')
plt.plot(X, model.predict(X), color='r', linewidth=2, label='Dropout Regularization')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Neural Network with Dropout Regularization')
plt.show()上述代碼生成了一些具有噪聲的樣本數據,并構建了一個簡單的具有Dropout正則化的神經網絡模型。通過繪制原始數據和擬合曲線,可以更好地理解Dropout正則化在神經網絡中的應用。
5、貝葉斯Ridge和Lasso回歸
貝葉斯Ridge回歸和Lasso回歸是兩種基于貝葉斯統計思想的回歸算法模型。它們都是經典的線性回歸的擴展,可以用于特征選擇和解決過擬合問題。
貝葉斯Ridge回歸
貝葉斯Ridge回歸通過引入正則化項來控制模型的復雜度,同時利用貝葉斯推斷方法進行參數估計。其優化目標是最小化損失函數和正則化項的和。
貝葉斯Ridge回歸的目標函數如下所示:
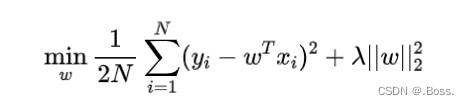
貝葉斯Ridge回歸的核心思想是將權重參數視為一個隨機變量,并使用貝葉斯推斷對其進行估計。
通過引入先驗分布p(W),根據貝葉斯定理可以得到后驗分布P(W|X,y)。然后,可以通過采樣或其他方法來估計權重參數的分布,從而得到預測結果。
貝葉斯Ridge回歸的優點是可以靈活地處理不同類型的數據和噪聲,并且可以用作特征選擇方法。缺點是計算復雜度較高,需要進行概率推斷。
貝葉斯Lasso回歸
貝葉斯Lasso回歸也是一種基于貝葉斯統計思想的回歸模型。它與貝葉斯Ridge回歸類似,但使用的是L1范數正則化項。
貝葉斯Lasso回歸的目標函數如下所示:
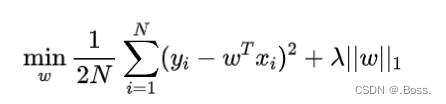
貝葉斯Lasso回歸通過最小化損失函數和L1范數正則化項來實現稀疏性。L1范數傾向于將一些權重參數設為0,從而實現特征選擇。
貝葉斯Lasso回歸的優點是可以自動進行特征選擇,并且能夠處理高維數據。缺點是計算復雜度較高,需要進行概率推斷。
以貝葉斯Ridge回歸為例,使用Python代碼實現:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge# 生成示例數據集
np.random.seed(42)
X = np.random.rand(100, 1) * 10
y = 2 * X[:, 0] + np.random.randn(100)# 創建貝葉斯Ridge回歸模型對象
model = BayesianRidge()# 擬合模型
model.fit(X, y)# 繪制原始數據和擬合曲線
fig, ax = plt.subplots()
ax.scatter(X, y, color='blue', label='Original data')# 生成用于預測的新樣本點
x_new = np.linspace(0, 10, 100).reshape(-1, 1)# 預測新樣本點的輸出值
y_pred, y_std = model.predict(x_new, return_std=True)# 繪制擬合曲線及置信區間
ax.plot(x_new, y_pred, color='red', label='Fitted curve')
ax.fill_between(x_new.flatten(), y_pred - y_std, y_pred + y_std, color='pink',alpha=0.5, label='Confidence interval')ax.set_xlabel('X')
ax.set_ylabel('y')
ax.set_title('Bayesian Ridge Regression')
ax.legend()
plt.show()6、早停法(Ear
早停法(Early Stopping)是一種用于防止模型過擬合的正則化技術。它通過在訓練過程中監測驗證誤差,并根據驗證誤差的變化來確定何時停止訓練模型,以避免過擬合。
早停法采用以下步驟:
-
將數據集劃分為訓練集和驗證集。
-
初始化模型參數。
-
在每個訓練迭代中,計算訓練誤差并更新模型參數。
-
在每個訓練迭代后,計算驗證誤差。
-
如果驗證誤差開始上升,則停止訓練,并使用具有最低驗證誤差的模型參數作為最終模型。
公式:
早停法的目標是在驗證誤差開始上升之前找到最佳模型,即訓練誤差和驗證誤差同時達到較小值的點。
下面是一個Python實現的案例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression# 生成示例數據
np.random.seed(42)
X = np.linspace(-5, 5, num=100).reshape(-1, 1)
y = 2 * X + np.random.normal(0, 1, size=(100, 1))# 劃分訓練集和驗證集
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)# 創建線性回歸模型對象
model = LinearRegression()# 記錄訓練誤差和驗證誤差
train_errors = []
val_errors = []# 擬合數據并記錄誤差
for i in range(1, len(X_train)):model.fit(X_train[:i], y_train[:i])y_train_pred = model.predict(X_train[:i])y_val_pred = model.predict(X_val)train_errors.append(np.mean((y_train_pred - y_train[:i]) ** 2))val_errors.append(np.mean((y_val_pred - y_val) ** 2))# 繪制優化復雜圖形
fig, ax = plt.subplots()
ax.plot(train_errors, label="Train Error")
ax.plot(val_errors, label="Validation Error")best_epoch = np.argmin(val_errors)
ax.axvline(x=best_epoch, linestyle="--", color="red", label="Early Stopping")ax.set_xlabel("Epoch")
ax.set_ylabel("Mean Squared Error")
ax.set_title("Early Stopping")
ax.legend()
plt.show()代碼證,使用了線性回歸模型,并在每個訓練迭代中記錄了訓練誤差和驗證誤差。通過繪制訓練誤差和驗證誤差的曲線,以及早停法的標記點,可以更加直觀地觀察到模型的優化過程和選擇最佳模型時的判定點。
這樣,使用優化復雜的圖形可以更好地理解早停法算法模型的效果。
7、數據增強
數據增強正則化是一種常用的正則化技術,它通過對訓練數據進行隨機變換或擴充來增加數據集的多樣性。這種方法可以幫助模型更好地泛化,并減輕過擬合問題。
數據增強正則化的步驟如下:
1、對訓練數據進行一系列隨機的變換操作,例如旋轉、平移、縮放、裁剪等。
2、將變換后的樣本添加到原始訓練數據集中。
3、使用經過增強的數據集進行模型訓練。
數據增強正則化的目標是通過增加數據集的多樣性,使模型能夠更好地適應不同的輸入情況,并提高其泛化能力。
由于數據增強正則化是一種基于隨機變換的方法,沒有明確的公式表達。
代碼示例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.linear_model import LogisticRegression# 生成示例數據集
np.random.seed(42)
X, y = make_moons(n_samples=200, noise=0.1)# 創建Logistic回歸模型對象
model = LogisticRegression()# 繪制原始數據分布
fig, ax = plt.subplots()
ax.scatter(X[:, 0], X[:, 1], c=y, cmap="bwr", edgecolors='k')
ax.set_xlabel("X1")
ax.set_ylabel("X2")
ax.set_title("Original Data Distribution")# 數據增強
n_transforms = 50
augmented_X = []
augmented_y = []
for i in range(n_transforms):transformed_X = X + np.random.normal(0, 0.05, size=X.shape)augmented_X.append(transformed_X)augmented_y.append(y)augmented_X = np.concatenate(augmented_X, axis=0)
augmented_y = np.concatenate(augmented_y, axis=0)# 繪制經過數據增強后的數據分布
fig, ax = plt.subplots()
ax.scatter(augmented_X[:, 0], augmented_X[:, 1], c=augmented_y, cmap="bwr", edgecolors='k')
ax.set_xlabel("X1")
ax.set_ylabel("X2")
ax.set_title("Data Distribution after Augmentation")# 使用經過增強的數據進行模型訓練
model.fit(augmented_X, augmented_y)# 繪制決策邊界
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)fig, ax = plt.subplots()
ax.contourf(xx, yy, Z, alpha=0.8, cmap="bwr")
ax.scatter(X[:, 0], X[:, 1], c=y, cmap="bwr", edgecolors='k')
ax.set_xlabel("X1")
ax.set_ylabel("X2")
ax.set_title("Decision Boundary")plt.show()在代碼示例中,我們使用了make_moons函數生成了一個月亮形狀的二分類數據集。然后,通過對原始數據進行隨機的高斯擾動(np.random.normal),生成了多個變換后的樣本,并將這些樣本添加到原始數據集中。最后,使用經過增強的數據集訓練了Logistic回歸模型,并繪制了決策邊界。
通過增強后的數據集,模型能夠更好地捕捉到數據的不同特征和變化,使得模型能夠更好地區分兩個類別。而繪制的決策邊界顯示了模型在增強后的數據上學到的決策規則。
這種可視化方法有助于理解數據增強正則化的作用,以及如何通過引入多樣性來改善模型的泛化能力。
實際應用中可能需要根據具體情況進行調整或使用其他數據增強技術。同時,數據增強正則化算法模型有許多變體和技巧,可以根據具體任務和需求進行調整和改進。
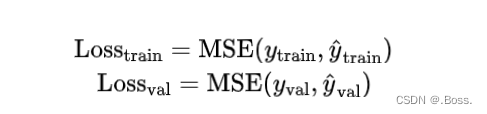



與dict協議(在線詞典))

)













