本章我們繼續講排序算法，這里我們將學習選擇排序，也是一個很普遍很常見的排序算法，邏輯和代碼都比較簡單，比較容易掌握，我們直接走起

選擇排序

基本思想：選擇排序（SelectSort），即每一次從待排序的數據元素中選出最小（或最大）的一個元素，存放在序列的起始位置，直到全部待排序的數據元素排完

我們這里以排升序為例

選擇排序與冒泡排序一樣，也分為內層循環和外層循環，內層循環是找出最小的元素放到未排序數組的第一位，外層循環按照內層邏輯，一步一步的將元素由小到大依次放到數組內，完成排序

單趟邏輯：單趟排序就是從記錄本次循環的第一個元素，依次向后比較，若后面的元素大于記錄的元素，那么就將記錄的元素換為更小的元素，并記錄此時記錄元素的下標，方便在出循環后進行交換，找到數組末尾，本次單趟循環結束，此時記錄的元素就是最小元素，那么我們就進行交換

整體邏輯：沿用單趟邏輯，多次進行排序，若有n個數據，那么就需要外層循環n-1次，將數據全部排好。

邏輯圖

代碼實現

void SelectSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int tmp = a[i];int k = i;for (int j = i + 1; j < n; j++){if (a[j] < tmp){tmp = a[j];k = j;}}Swap(&a[i], &a[k]);}
}

優化

思路：上面的選擇排序是基本的選擇排序，我們可以發現，他每次循環都需要遍歷未排序的數組去尋找最小的元素，那么我們換一種思路，如果我們在遍歷未排序的數組時，同時找到最大的元素和最小的元素，是不是就減少了一半的循環量，思路有了，我們就直接開始實現

總體的思路還是和上面大差不差，但是這次我們需要多建一個變量end，來記錄數組末尾的位置

然后依次進行遍歷，之前我們用tmp記錄最小的數，這里就需要用兩個變量max 和 min來分別記錄最大值和最小值，為了方便我們直接記錄下標，這樣就不用新建變量來記錄下標了，而且還可以直接進行比較

流程圖

?優化代碼（有瑕疵）

void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin < end){int min = begin;int max = begin;for (int i = begin + 1; i <= end; i++){if (a[i] > a[max]){max = i;}if (a[i] < a[min]){min = i;}}Swap(&a[begin], &a[min]);Swap(&a[end], &a[max]);begin++;end--;}
}

看了上面的分析和代碼的實現，也許你會認為，這樣就完成選擇排序的優化，但是事實真的如此嗎，先說結論，這個排序邏輯確實是這樣的，代碼基本也是對的，可以完成大多數的排序，但是有個別情況，是無法進行正確排序的，因此上面實現的是有瑕疵的

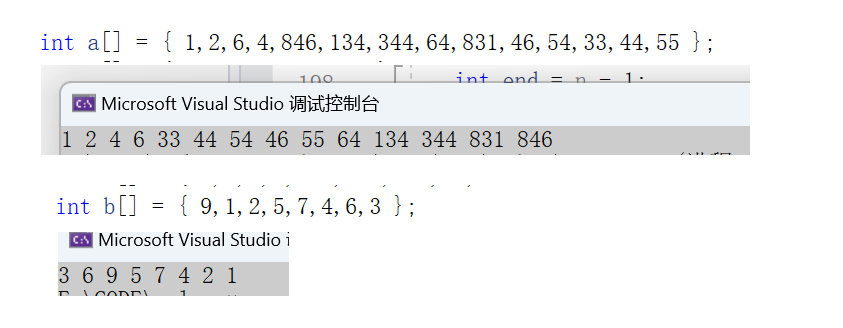
我們來分析一下，當第一輪排序時，我們上面的代碼會記錄

max為0，min為 1 ，begin為0，end為7

進行交換的時候，先交換begin和min

結果為 1? ?9? 2? ?5? ?7? 4? ?6? 3

再交換max和end的時候

結果為 3? ? 9? ? 2? ? 5? ?7? ? 4? ?6? ?1

很顯然，已經出錯了，max在和end進行交換的時候，max已經變換了位置，因此我們找到了問題，找到了問題之后，我們就需要解決問題

我們只需要加一個判斷條件，當最大值為begin時，第一步begin和min交換就會把max的值交換走，這時我們需要進行判斷，如果begin==max，那么就將max的值賦為min，即此時最大值被交換到的位置，再進行第二步交換即可。

優化代碼最終實現

void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin + 1; i <= end; ++i){if (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}Swap(&a[begin], &a[mini]);if (begin == maxi)maxi = mini;Swap(&a[end], &a[maxi]);++begin;--end;}
}

?總結（冒泡排序和選擇排序的區別）

冒泡排序的時間復雜度為O(n^2)，其中n是要排序的元素數量。這是因為冒泡排序需要進行多次遍歷，每次遍歷都需要比較和交換元素。因此，對于大規模數據的排序，冒泡排序可能不是最有效的選擇。
選擇排序的時間復雜度也是O(n^2)，但它的性能通常優于冒泡排序。因為選擇排序只需要進行一次遍歷，并且只需要進行一次比較和交換操作。因此，在處理大規模數據時，選擇排序通常更為高效。

但如果遇到已經排好序的數據，冒泡排序只需要循環一次就能發現，并終止，但選擇排序卻需要繼續遍歷數組，在這一點上選擇排序的效率是不如冒泡排序的。