Adapting to Unknown Low-Dimensional Structures in Score-Based Diffusion Models
公和眾和號:EDPJ(進 Q 交流群:922230617 或加 VX:CV_EDPJ 進 V 交流群)
![]()

目錄
0. 摘要
1. 引言
1.1 擴散模型
1.2 現有結果的不足
1.3 我們的貢獻
2. 問題設置
3. 主要結果
3.1 收斂性分析
3.2 系數設計的唯一性
4. 對 DDPM 采樣器的分析(定理 1 證明)
5. 討論
0. 摘要
本文研究基于分數的擴散模型,其目標分布集中于或接近其所在的高維空間中的低維流形,這是自然圖像分布的常見特征。盡管先前已有嘗試理解擴散模型的數據生成過程,但在存在低維結構的情況下,現有理論支持仍然非常不足。本文增強了這一點。對于流行的去噪擴散概率模型(DDPM),我們發現每個去噪步驟中誤差對環境維度 d 的依賴通常是不可避免的。我們進一步識別出一種獨特的系數設計,使得收斂速率達到 O(k^2 / √T) 的數量級(最高可達對數因子,up to log factors),其中 k 是目標分布的內在維度,T 是步驟數量。這代表了第一個理論證明,表明 DDPM 采樣器能夠適應目標分布中未知的低維結構,突顯了系數設計的重要性。所有這些都是通過一組新穎的分析工具實現的,這些工具以更確定的方式刻畫了算法動態。?
1. 引言
基于分數的擴散模型是一類生成模型,因其能夠從復雜分布(如圖像、音頻和文本)中生成高質量的新數據實例而在機器學習和人工智能領域中獲得了廣泛關注(Dhariwal 和 Nichol,2021;Ho 等,2020;Sohl-Dickstein 等,2015;Song 和 Ermon,2019;Song 等,2021)。這些模型通過逐漸將噪聲轉化為目標分布的樣本來運行,該過程由預訓練的神經網絡引導,這些神經網絡近似得分函數。在實際應用中,得分驅動擴散模型在各個領域生成現實且多樣的內容方面表現出了顯著的性能,達到了生成式 AI 的最新技術水平(Croitoru 等,2023;Ramesh 等,2022;Rombach 等,2022;Saharia 等,2022)。
1.1 擴散模型
基于分數的擴散模型的發展深深植根于隨機過程的理論。在高層次上,我們考慮一個前向過程:
![]()
其中從目標數據分布中抽取一個樣本(即 X0~p_data),然后逐漸將其擴散為高斯噪聲。擴散模型的關鍵在于構造一個反向過程:
![]()
![]()
該過程從純高斯噪聲開始(即 Y_T~N(0,I_d)),并逐漸將其轉化為一個新的樣本 Y0,其分布與 p_data 相似。
經典的關于隨機微分方程(SDEs)時間反轉的結果(Anderson,1982;Haussmann 和 Pardoux,1986)為上述任務提供了理論基礎。考慮一個連續時間的擴散過程:
![]()
對于某個函數 β:[0,T]→R^+,其中 (Wt)_(0≤t≤T) 是標準布朗運動。對于廣泛的函數 β,這個過程以指數速度收斂到高斯分布。設 p_(Xt) 為 Xt 的密度。可以構造一個反向時間的 SDE:
![]()
其中 (Zt)_(0≤t≤T) 是另一個標準布朗運動。定義 Y_t= ? Y_(T?t?)。眾所周知,對于所有 0≤t≤T,
![]()
這里,?log? p_(Xt) 被稱為 Xt 的分布的得分函數,它并不顯式已知。
上述結果激發了以下范式:我們可以通過時間離散化擴散過程(1.3)來構建前向過程(1.1),并通過離散化反向時間 SDE(1.4)和從數據中學到的得分函數來構建反向過程(1.2)。這種方法催生了流行的 DDPM 采樣器(Ho等,2020;Nichol 和 Dhariwal,2021)。盡管 DDPM 采樣器的理念根植于 SDE 理論,但本文中提出的算法和分析不需要任何 SDE 的先驗知識。
本文通過建立反向過程輸出分布與目標數據分布之間的接近性來檢驗 DDPM 采樣器的準確性。由于在完美得分估計的連續時間極限中,這兩個分布是相同的,DDPM 采樣器的性能受到兩種誤差來源的影響:離散化誤差(由于有限的步驟數量)和得分估計誤差(由于得分估計的不完美)。本文將得分估計步驟視為一個黑箱(通常通過訓練大型神經網絡來解決),重點研究時間離散化和不完美的得分估計如何影響 DDPM 采樣器的準確性。
1.2 現有結果的不足
過去幾年中,人們對研究 DDPM 采樣器的收斂保證產生了極大的興趣(Benton等,2023;Chen等,2023a,c;Li等,2024)。為了便于討論,我們考慮一個理想的設置,即完美得分估計。在這種情況下,現有結果可以解釋如下:要達到 ε-精度(即目標分布與輸出分布之間的總變差距離(total variation distance)小于ε),需要采取超過 poly(d)/ε^2 數量級的步驟(最高可達對數因素),其中 d 是問題的維度。在這些結果中,最先進的是 Benton 等(2023),其實現了對維度 d 的線性依賴。
然而,DDPM 采樣器的實際性能與現有理論之間似乎存在顯著差距。例如,對于兩個廣泛使用的圖像數據集,CIFAR-10(維度 d = 32×32×3)和 ImageNet(維度 d ≥ 64 × 64 × 3),已知 50 和 250 步驟(也稱為 NFE,函數評估次數)足以生成良好的樣本(Dhariwal和Nichol,2021;Nichol和Dhariwal,2021)。這與上述現有理論保證形成鮮明對比,后者建議步驟數量 T 應超過維度 d 的數量級以達到良好性能。
實證證據表明,自然圖像的分布集中在它們存在的高維空間中的低維流形上或附近(Pope等,2021;Simoncelli和Olshausen,2001)。鑒于此,一個合理的推測是,DDPM 采樣器的收斂速度實際上取決于內在維度而非環境維度。然而,當目標數據分布的支持集具有低維結構時,對擴散模型的理論理解仍然非常欠缺。作為一些最近的嘗試,De Bortoli(2022)在Wasserstein-1度量下建立了第一個收斂保證。然而,他們的誤差界限對環境維度 d 具有線性依賴,并且對低維流形的直徑具有指數依賴。另一個最近的工作(Chen等,2023b)主要關注利用低維結構的適當選擇的神經網絡進行得分估計,這也不同于我們的主要關注點。
1.3 我們的貢獻
鑒于理論與實踐之間的巨大差距以及先前結果的不足,本文邁出了理解在目標數據分布具有低維結構時 DDPM 采樣器性能的一步。我們的主要貢獻可以總結如下:
- 我們表明,通過特定的系數設計,評估 X1 和 Y1 的法則(laws)的總變差距離的 DDPM 采樣器的誤差上限為:
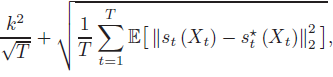
- 該上限最高可達對數因子(logarithmic factors),其中 k 是目標數據分布的內在維度(將稍后嚴格定義),并且 s*_t(對應于?st)是在每一步的真實(對應于學到的)得分函數。第一項代表離散化誤差(隨著步驟數 T 趨向無窮大而消失),而第二個項應被解釋為得分匹配誤差。該界限幾乎與維度無關——環境維度 d 僅出現在對數項中。
- 我們還表明,我們選擇的系數在某種意義上是獨特的調度(schedule),它不會在每一步產生與環境維度 d 成比例的離散化誤差。這與沒有低維結構的一般設置形成鮮明對比,在一般設置中,相當廣泛的系數設計可以導致對 d 具有多項式依賴的收斂速度。此外,這證實了通過精心設計系數可以提高 DDPM 采樣器性能的觀察結果(Bao等,2022;Nichol和Dhariwal,2021)。 據我們所知,本文提供了第一個理論,證明了 DDPM 采樣器在適應未知低維結構方面的能力。
2. 問題設置
在本節中,我們介紹擴散模型和DDPM采樣器的一些預備知識和關鍵成分。
前向過程。我們考慮形式如下的前向過程(1.1):
![]()
![]()
其中,學習率 β_t ∈ (0, 1) 將在稍后指定。對于每個 t >=?1,X_t 在 R^d 上具有概率密度函數(PDF),我們將用 q_t 表示 X_t 的法則(law)或 PDF。設
![]()
可以直接驗證,
![]()
我們將選擇學習率 βt 以確保?ˉαT 變得極小,使得 q_T ≈ N(0,I_d)。
得分函數。構建 DDPM 采樣器的反向過程的關鍵成分是與每個 qt 相關的得分函數 s*_t:Rd→Rd,定義為
![]()
這些得分函數不是顯式已知的。這里我們假設可以訪問每個 s*_t(·) 的估計值 st(?),并定義平均的 ?2? 得分估計誤差為

此量度捕捉了我們理論中不完美得分估計的影響。
DDPM 采樣器。為了構建反向過程(1.2),我們使用 DDPM 采樣器:
![]()
![]()
其中,ηt,σt>0 是超參數,在目標數據分布具有低維結構時對 DDPM 采樣器的性能起著重要作用。正如我們將看到的,我們的理論建議如下選擇:
![]()
對于每個 1≤t≤T,我們將用 pt 表示 Y_t 的 law 或 PDF。
目標數據分布。令 X ? R^d 為目標數據分布 p_data 的支持集,即滿足 p_data(C)=1 的最小閉集?C ? R_d。為了最大限度地實現一般性,我們使用 ε-net 和覆蓋數(covering number)的概念(參見 Vershynin (2018))來表征 X 的內在維度。對于任意 ?>0,如果對于 X 中的任意 x∈X,都存在某個 N_? ? X 中的 x′ 滿足
![]()
則稱 N_? 是 X 的 ε-net。覆蓋數 N_?(X) 定義為 X 的 ε-net 的最小可能基數。
- (低維性)固定 ?=T^(?c_?),其中 c_?>0 是某個足夠大的通用常數。我們將 X 的內在維度定義為某個量 k>0,使得對于某個常數 C_cover>0,下式成立。
![]()
- (有界支持)假設存在一個通用常數 c_R>0,使得下式成立。也就是說,我們允許 X 的直徑隨著步驟數 T 以多項式增長。
![]()
我們的設置允許 X 集中在低維流形上或其附近,這比假設精確的低維結構更寬松。作為一個合理的檢查,當 X 位于 Rd 的 r-維子空間中時,標準體積論證(standard volume argument)(參見 Vershynin (2018, Section 4.2.1))給出
![]()
![]()
表明在這種情況下內在維度 k 的數量級為 r。
學習率調度(schedule)。按照 Li 等(2024)的方法,我們采用以下學習率調度:
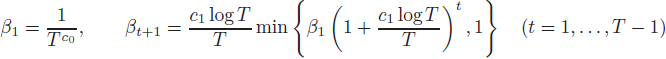
對于某些足夠大的常數 c0,c1>0。此安排不是唯一的——任何其他滿足引理 8 中性質的 βt 安排都可以在本文中得到相同的結果。
3. 主要結果
我們現在可以提出 DDPM 采樣器的主要理論保證。
3.1 收斂性分析
我們首先提出 DDPM 采樣器的收斂性理論。證明見第 4 節。
定理 1:假設我們采用 DDPM 采樣器(2.3)的系數 ηt = η*_t 和 σt = σ*_t(參見(2.4)),則存在某個通用常數 C>0,使得(全變差距離,total variation)
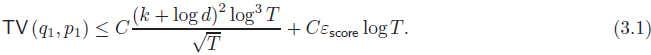
定理 1 帶來幾個重要的推論。公式 (3.1) 中的兩個項分別對應于離散化誤差和得分匹配誤差。暫時假設得分估計完美(即 ?_score=0),我們的誤差界限 (3.1) 表示要達到 ? 精度的迭代復雜度為 k^4/?^2(最高可達對數因子),對于任何非平凡的目標精度水平 ?<1。在不存在低維結構的情況下,即目標數據分布的內在維度 k 漸進等于環境維度(高維空間的維度) d:
![]()
我們的結果也恢復了 Benton 等(2023);Chen 等(2023a,c);Li 等(2024)中階數為 poly(d)/?^2 的迭代復雜度。這表明,我們的系數選擇 (2.4) 使得 DDPM 采樣器能夠適應目標數據分布中可能存在的(未知的)低維結構,并且在最一般的設置中仍然是一個有效的標準。公式 (3.1) 中的得分匹配誤差與 ?_score 成正比,這表明 DDPM 采樣器對不完美的得分估計具有穩定性。
3.2 系數設計的唯一性
本節中,我們研究了系數設計在 DDPM 采樣器適應內在低維結構中的重要性。我們的目標是展示,除非根據 (2.4) 選擇 DDPM 采樣器 (2.3) 的系數 ηt?,否則在每一步去噪過程中都會出現與環境維度 d 成正比的離散化誤差。
在本文以及大多數先前的 DDPM 文獻中,對誤差(全變差距離,total variation) TV(q1,p1?) 的分析通常從以下分解開始:
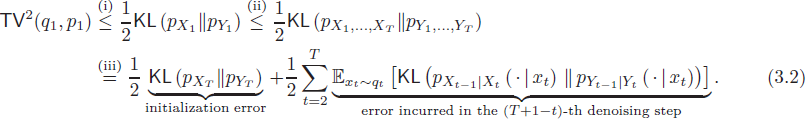
這里步驟 (i) 由 Pinsker 不等式得出,步驟 (ii) 利用數據處理不等式,而步驟 (iii) 使用了 KL 散度的鏈規則。我們可以將上述分解中的每一項解釋為每一步去噪過程中引起的誤差。事實上,這個分解也與逆過程負對數似然的變分界限密切相關,這是訓練 DDPM 的優化目標(Bao 等,2022;Ho 等,2020;Nichol 和 Dhariwal,2021)。
我們考慮目標分布 p_data=N(0,I_k),其中 I_k∈R^(d×d) 是一個對角矩陣,滿足 I_(i,i)=1 對于 1≤i≤k 和 I_(i,i)=0 對于 (k+1)≤i≤d。這是一個在 R^d 上支持在 k 維子空間上的簡單分布。我們的第二個理論結果為這種目標分布的每一步去噪過程中引起的誤差提供了下界。證明見附錄 B。
定理 2:考慮目標分布 p_data=N(0,I_k),假設 k≤d/2。對于具有完美得分估計的 DDPM 采樣器(即,st(?)=s*_t(?) 對所有 t)和任意系數 ηt,σt>0,我們有
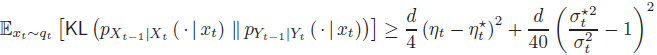
對于每個 2≤t≤T。參見 (2.4) 中 η*_t 和 σ*_t?的定義。
定理 2 表明,除非我們選擇 η_t 和 (σ_t)^2?與 η*_t 和?(σ*_t)^2?相同(或極為接近),否則相應的去噪步驟會產生一個與環境維度 d 成線性關系的不期望誤差。這凸顯了系數設計對于 DDPM 采樣器的關鍵重要性,特別是當目標分布顯示低維結構時。
最后,我們要注意上述論點僅展示了系數設計對誤差上界 (3.2) 的影響,而不是對誤差本身的影響。可能存在更廣泛的系數范圍可以導致維度無關的誤差界限(如 (3.1)),而誤差上界 (3.2) 仍然維度相關。這需要新的分析工具(因為我們不能在分析中使用寬松的上界 (3.1)),我們將在未來的工作中討論。
4. 對 DDPM 采樣器的分析(定理 1 證明)
本節致力于建立定理 1。其思想是限制每個去噪步驟中的誤差,如在分解(3.2)中描述的那樣,即對于每個 2 ≤ t ≤ T,我們需要限制
![]()
這需要連接兩個條件分布 p_(X_(t?1)) | Xt 和 p_(Y_(t?1)) | Yt。通過引入輔助隨機變量
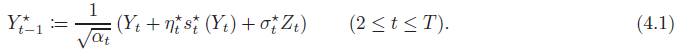
來方便地將時間離散化誤差與不完美的評分估計誤差分離。
從高層次來看,對于每個 2 ≤ t ≤ T,我們的證明包括以下步驟:
- 確定一個典型集合 At ? Rd × Rd,使得 (Xt,Xt?1) ∈ At 的概率很高。
- 建立點對點的近似?
![]()
- 描述由于不完美的評分估計導致的 p_(Y*_(t?1)) | Yt 與 p_(Y_(t?1)) | Yt 的偏差。
5. 討論
本文研究了當目標分布集中于或接近低維流形時的 DDPM 采樣器。我們確定了一種特定的系數設計,使得 DDPM 采樣器能夠適應未知的低維結構,并建立了一個維度自由(dimension-free)的收斂速率 k^2 / √T(最高可達對數因子)。
我們通過指出幾個值得未來研究的方向來總結本文。
- 首先,我們的理論得出的迭代復雜度在內在維度 k 上是四次的,這可能是次優的。改善這種依賴性需要更精細的分析工具。
- 此外,正如我們在第 3.2 節末尾討論的那樣,我們的系數設計(2.4)是否在實現維度無關誤差 TV(q1, p1) 方面是唯一的,這一點并不清楚。
- 最后,為 DDPM 采樣器開發的分析思想和工具可能被擴展到研究另一種流行的 DDIM 采樣器。?


)



 IP 地址)





)
)


)


