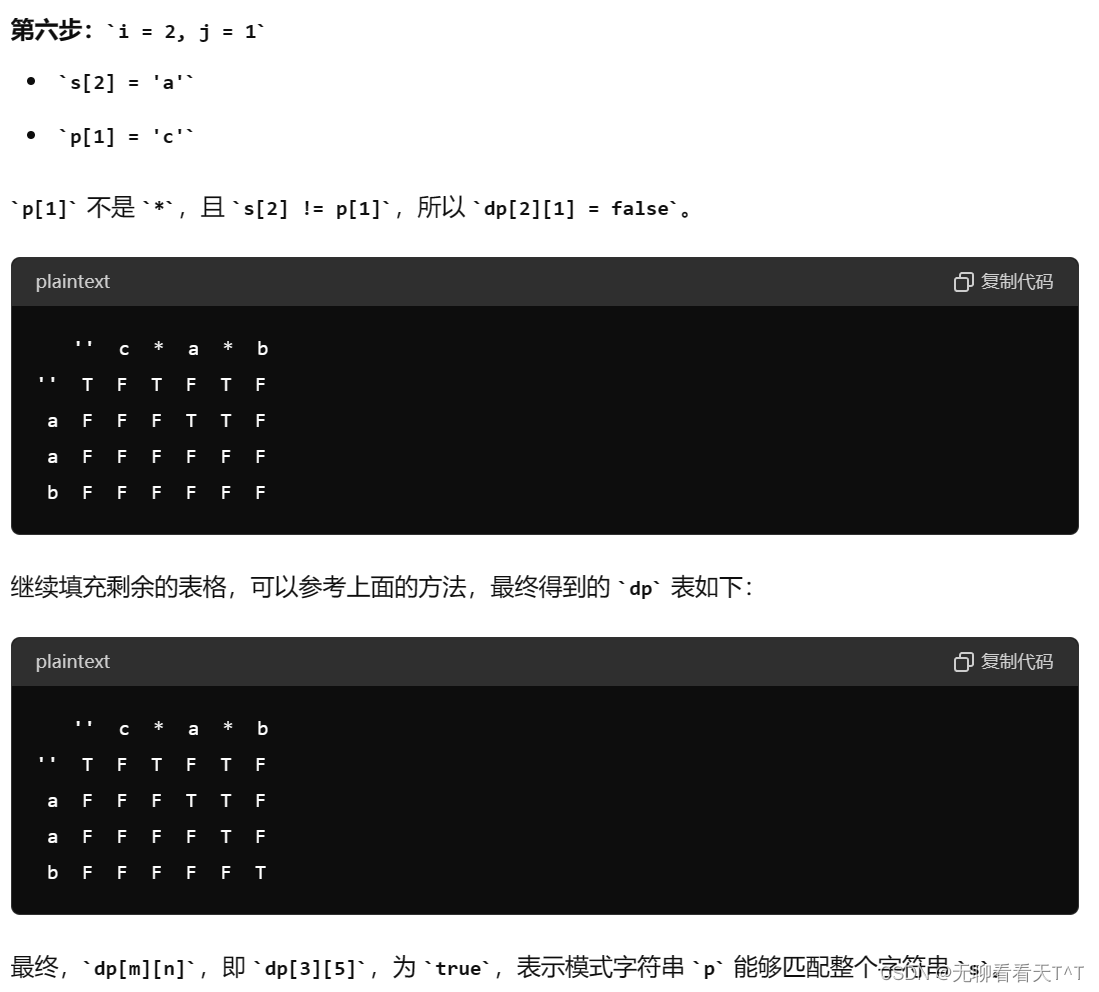
目錄

普通版本（動態規劃）

狀態表示

狀態轉移方程

優化③①情況

數學化簡分析

結合實際情況畫圖化簡分析

總結

最終代碼

---

題目鏈接：10. 正則表達式匹配 - 力扣（LeetCode）

好像是leetcode前100道里面最難的一道？我是fw🤡

普通版本（動態規劃）

題目條件：

• '.'?匹配任意單個字符
• '*'?匹配零個或多個前面的那一個元素（將其理解為*號，某字符*表示可以有n個該字符）
• 每次出現字符?*?時，前面都匹配到有效的字符（只有a~z*、.*兩種情況）

注意事項：字符*，變化的多出來的字符是向后延申的

條件解析與示例分析：

示例1：s = "aa"、p = "a"，可匹配

示例2：s = "aa"、p = "a*"，a*是一個整體，可以表示0~n個a，可匹配

示例3：s = "ab"、p = ".*"，.*是一個整體，可以表示0~n個.，每個.可代表任意字符，可匹配

示例4：s = "aab"、p = "d*a*b"，將d*視為一個空串，a*表示兩個a，b不變，可匹配

狀態表示

分析：由題意得我們可以要判斷的是p中[0,j]范圍內的字符是否能匹配s中[0,i]范圍內的字符，涉及了兩個數組間情況得判斷

結論：狀態轉移方程為dp[i][j]，該方程表示p[0,j]范圍內的子串是否可以匹配s[0,j]范圍內的子串?

狀態轉移方程

主旨：根據p數組最后位置的取值進行分情況討論（s[i]和p[j]分別表示s和p數組最后位置的字符）

①p[j]是a~z的字符

滿足? p[j] == s[i] && dp[i-1][j-1] == true 時dp[i][j]為真（當前和之前所有位置都為真）

②p[j]是字符.

滿足dp[i-1][j-1]==true，則dp[i][j]為真（只要之前均為真，.必可使最后一個位置也相同）

③p[j]是*?

③①p[j-1]是.

③①①.*表示空串

• 此時p[j-1]和p[j]位置報廢，若dp[i][j-2]為真則dp[i][j]為真，即p的[0,j-2]范圍內的字符能否與s的[0,i]范圍內的字符匹配

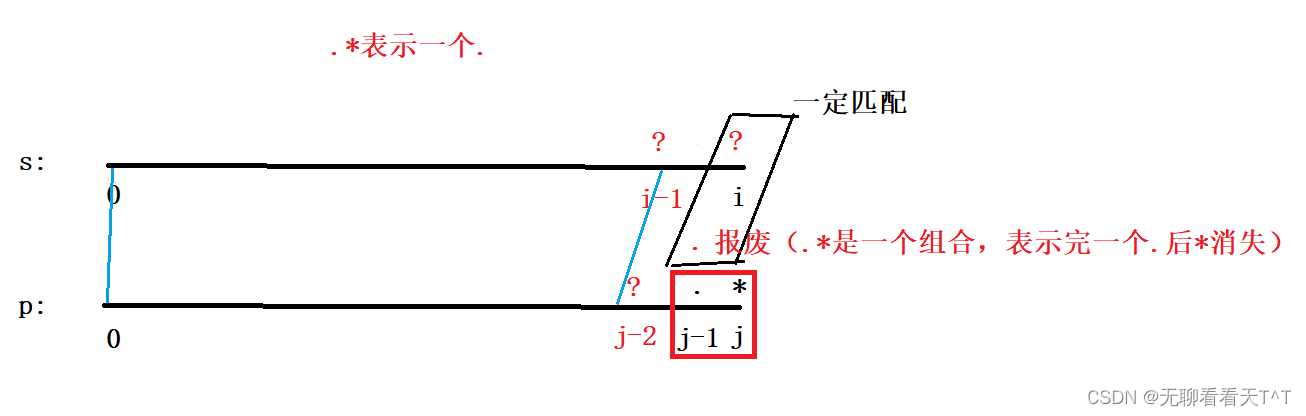
③①②.*表示一個.

• 此時p[j]位置報廢p[j-1]位置為.，若dp[i-1][j-2]為真則dp[i][j]為真，即p的[0,j-2]范圍內的字符能否與s的[0,i-1]范圍內的字符匹配，因為p[j-1]位置的.能表示任意字符，故s[i-1]位置不論是什么字符dp[i-1][j-1]一定為真

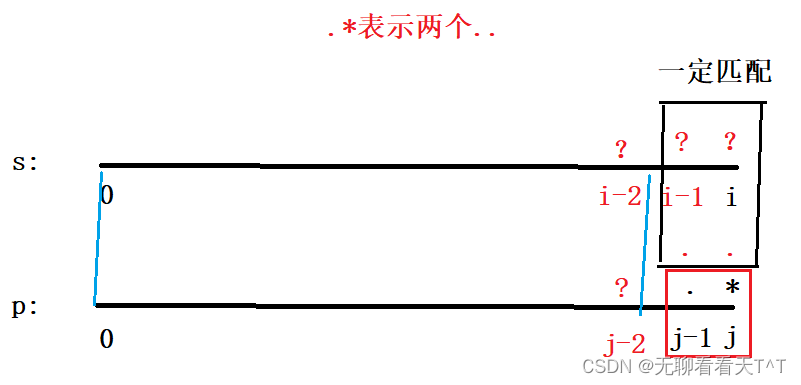
③①③.*表示兩個.

• 此時p[j]和p[j-1]位置均為.，若dp[i-2][j-2]為真則dp[i][j]為真，即p的[0,j-2]范圍內的字符能否與s的[0,i-2]范圍內的字符匹配，因為p[j]和p[j-1]位置的.能表示任意字符，故s[i]h和s[i-1]位置不論是什么字符dp[i][j]和dp[i-1][j-1]一定為真

③①④.*表示三個.

• 此時p[j]和p[j-1]均為甚至p[j+1]位置均為.，若dp[i-3][j-2]為真則dp[i][j]為真，即p的[0,j-2]范圍內的字符能否與s的[0,i-3]范圍內的字符匹配...（都一樣不重復解釋了）

③②p[j-1]是a~z的字符

③②①字符*表示空串

• 此時p[j-1]和p[j]位置報廢，若dp[i][j-2]為真則dp[i][j]為真（與上面一樣了，不解釋了）

③②②判斷j-1位置的字符是否與i位置相同（p[j-1] == s[i]）

• 相同則保留字符*的狀態，此時若dp[i-1][j]為真則dp[i][j]為真，因為s[j-1]位置上的字符與i位置匹配后因為可以用*造出很多個該字符，所以只需考慮p[0,j]范圍內的字符能否與s[0,i-1]范圍內的字符匹配即可（而判斷這一個范圍內的情況，就需要再次到③②②這種情況來進行判斷），如果均匹配則讓*造字符時多加一個該字符即可

優化③①情況

優化結果：當p[j]為*、p[j-1]為.時，dp[i][j] = dp[i][j-2] || dp[i-1][j]

初步分析：由③①中的多條結論可以得出，當滿足其中一個結論時，dp[i][j]就為真，因為此時p[j-1]和p[j]的組合為.*，如果dp[i][j-2]為真，那么.*只需要創建出一個.即可，如果dp[i-3][j-2]為真，那么.*只需要創建出三個.即可，即只要前面的相等，后面的.*就絕對可以保證后面的所有都相等，即：①p[j] == '*'時，dp[i][j] = dp[i][j-2] ||??dp[i-1][j-2] || dp[i-2][j-2] ...，但是這個式子還是有點長，那么是否能繼續化簡一下？

數學化簡分析

我們令i=i-1，重新套入上面的式子可得：

②p[j] == '*'時，dp[i-1][j] = dp[i-1][j-2] ||??dp[i-2][j-2] || dp[i-3][j-2] ...

我們發現，滿足dp[i-1][j]為真需要滿足dp[i-1][j-2] ||??dp[i-2][j-2] || dp[i-3][j-2] ...的某個條件為真，而該條件與①中的后半部分完全相同，由簡單的數學等價替換就可以得到我們優化③①情況的優化結果

結合實際情況畫圖化簡分析

當p[j]為*、p[j-1]為.時，我們可以分為兩種情況：

情況一：當.*組合與s[i]相同后后不變化仍然保留.*組合，接著比較s[i-1]，如果dp[i-1][j]為真則dp[i][j]為真（s的[0,i-1]范圍內的字符與p[0,j]范圍內的字符可以匹配）

情況二：將.*視為一個空串，那么此時如果dp[i][j-2]為真，則dp[i][j]也就為真

總結

1、①和②可以總結為一種情況：當p[j]==s[i]?或者 p[j]==.?為真 且dp[i-1][j-1]為真（兩個的末尾都匹配了 或者 p的末尾為.時無論s的末尾為什么字符都能匹配），那么dp[i][j]就為真

2、③可以總結為：當 dp[i][j-2] 為真或者?（p[j-1] == '.' || p[j-1] == s[i]）一個為真且?dp[i-1][j] 為真，則dp[i][j]為真（整合后p[j]==*時引發的所有結論，可以發現這些結論的本質就是圍繞p[j-1]*的組合是空串還是非空串進行研究并得出結論的）

• p[j-1]*的組合為空：由上圖的分析得，當p[j]為*時一定有“某字符*”是空串的情況，故可以將③①和③②為空的情況合并得到判斷dp[i][j]是否為空的一個條件dp[i][j-2]
• p[j-1]*的組合不為空：當p[j-1]為.時該組合為“.*”，此時只要dp[i-1][j]為真即可（上面優化里的當dp[j]為*、p[j-1]為.時dp[i][j]為真的兩個條件dp[i][j-2] || dp[i-1][j]，p[j-1]*組合為空時候占用了一個dp[i][j-2]，現在就剩下另一個條件了，當然如果你不信也可以再推一遍），當p[j-1]為a~z的字符時該組合為“a~z的字符*”，此時也是只需要dp[i-1][j]為真即可

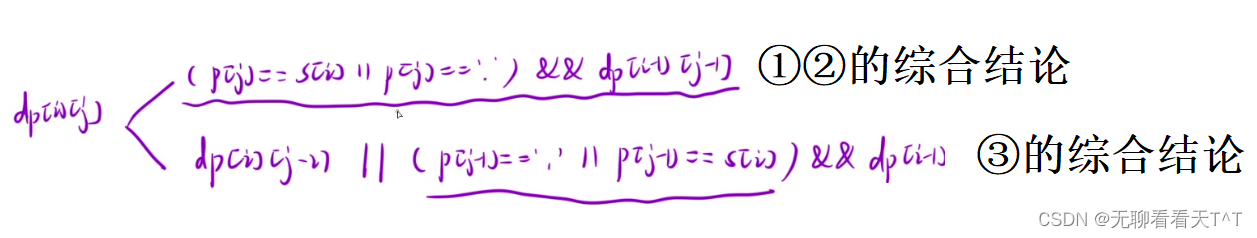
最終代碼

class Solution {
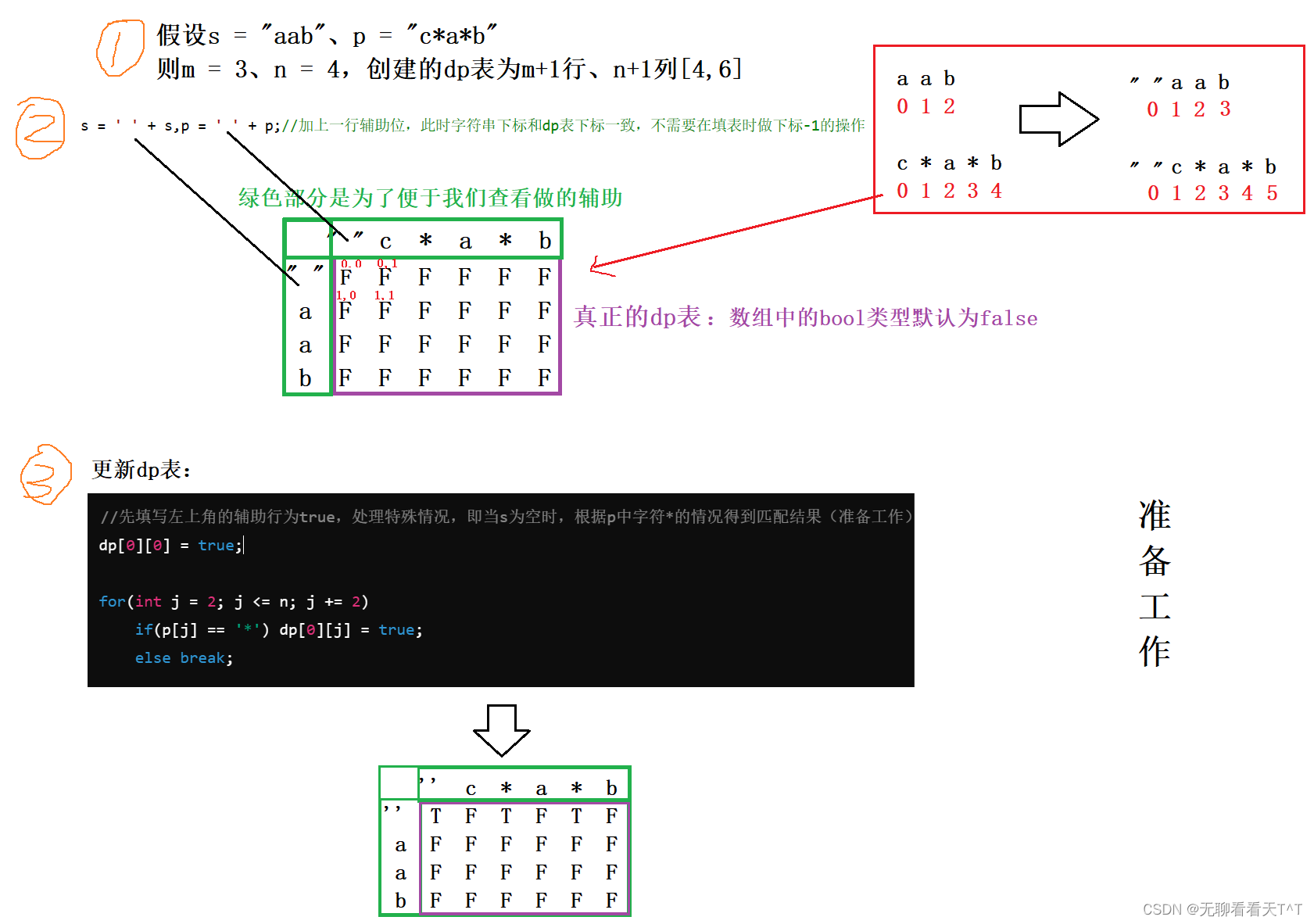
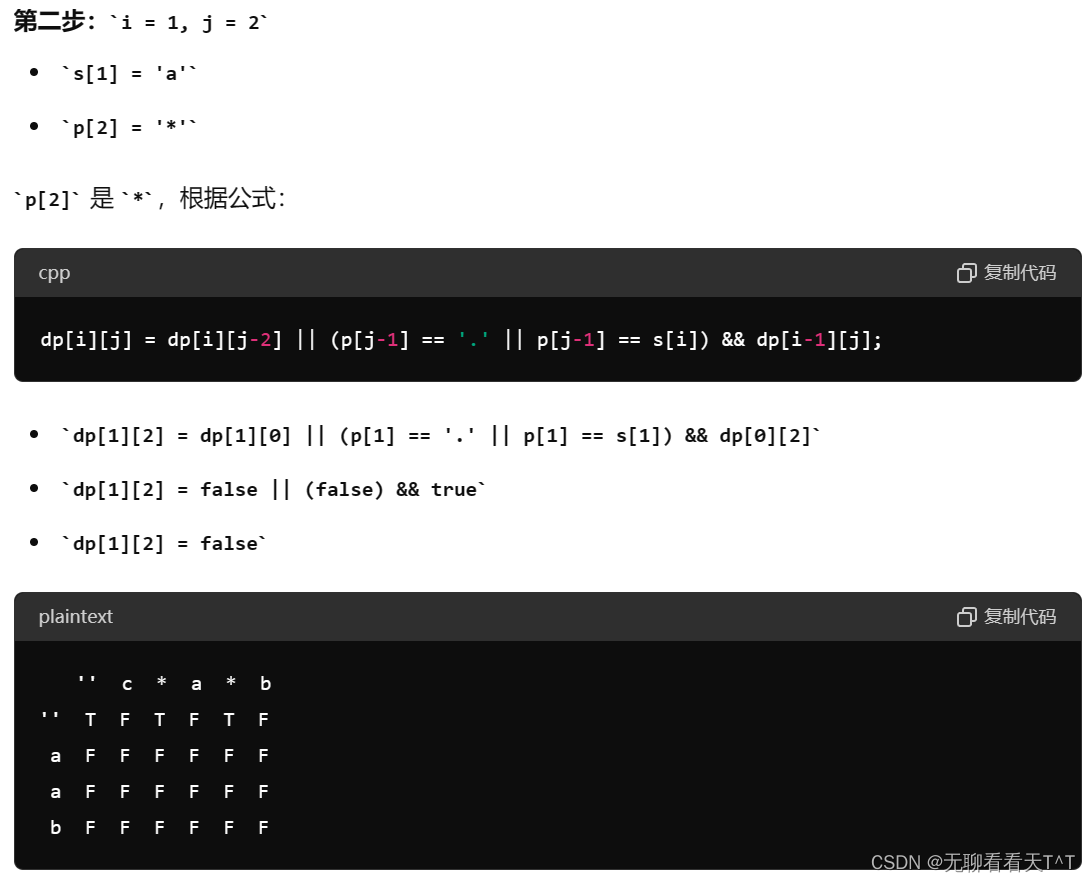
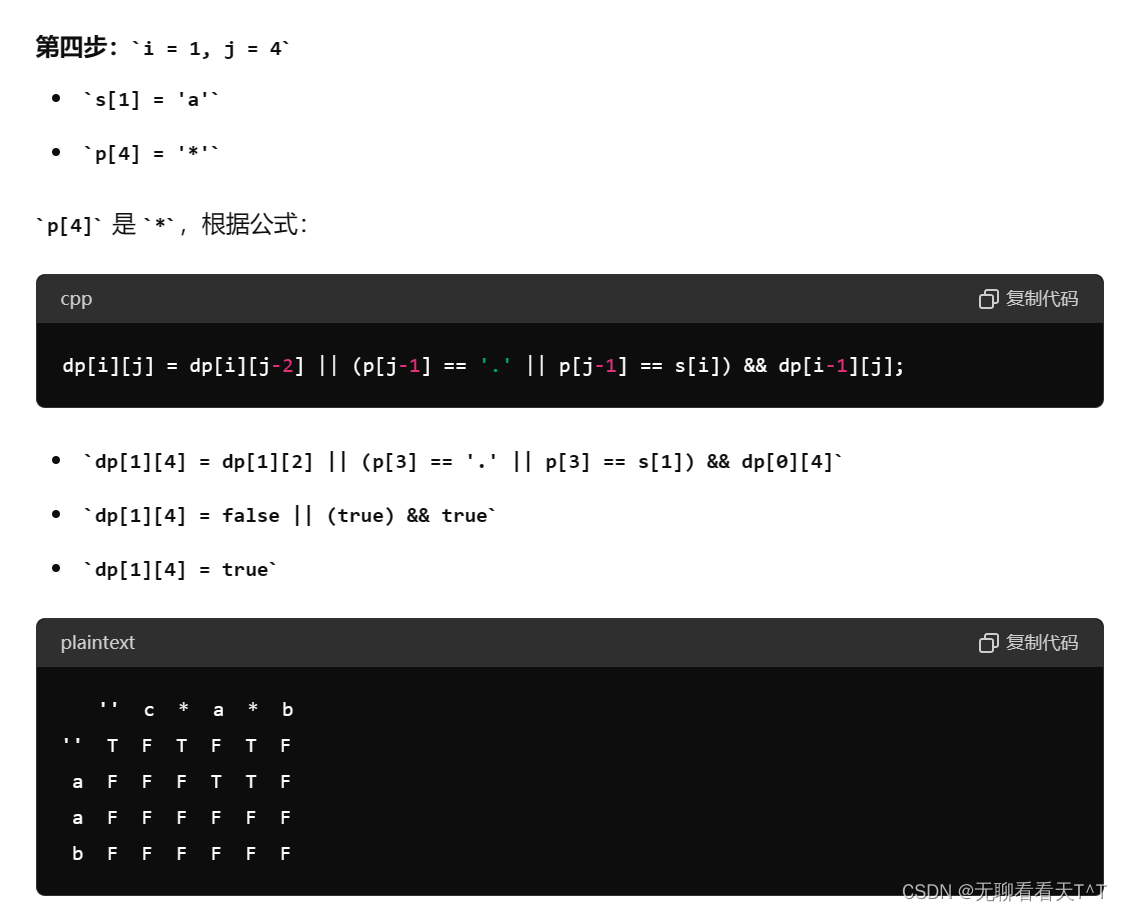
public:bool isMatch(string s, string p) {int m = s.size(),n = p.size();//二者大小不一樣相同//1、創建dp表vector<vector<bool>> dp(m+1,vector<bool>(n+1));//創建一個m行n列的dp表，+1是為了創建輔助行//2、初始化s = ' ' + s,p = ' ' + p;//加上一行輔助位，此時字符串下標和dp表下標一致，不需要在填表時做下標-1的操作//先填寫左上角的輔助行為true，處理特殊情況，即當s為空時，根據p中字符*的情況得到匹配結果（準備工作）dp[0][0] =true;//更新dp表for(int j = 2;j<=n;j+=2)if(p[j]=='*') dp[0][j] =true;else break;//3、填表for(int i = 1;i <= m;i++){for(int j = 1;j <= n;j++){//p[j]為*L:③的所有情況得到的結論if(p[j] == '*'){dp[i][j] = dp[i][j-2] || (p[j-1] == '.' || p[j-1] == s[i]) && dp[i-1][j];}//p[j]不為*:①②兩種情況得到的結論else{dp[i][j] = (p[j] == s[i] || p[j] == '.')&&dp[i-1][j-1];}}}//4、返回值return dp[m][n];//題目要求的是完全匹配，所以判斷范圍為[0,m]和[0,n];}
};

自我總結：動規主要的內容就是確認狀態表示和狀態轉移方程，由特例推廣至全部，只需要直到宏觀規律即可

~over~