目錄

分組數據回歸

---

分組數據回歸

并非所有數據點都是一樣的。 如果我們再次查看我們的 ENEM 數據集，相比小規模學校的分數，我們更相信規模較大的學校的分數。 這并不是說大型學校更好或什么， 而只是因為它們的較大規模意味著更小的方差。

import warnings
warnings.filterwarnings('ignore')import pandas as pd
import numpy as np
from scipy import stats
from matplotlib import style
import seaborn as sns
from matplotlib import pyplot as plt
import statsmodels.formula.api as smfstyle.use("fivethirtyeight")np.random.seed(876)
enem = pd.read_csv("./data/enem_scores.csv").sample(200)
plt.figure(figsize=(8,4))
sns.scatterplot(y="avg_score", x="number_of_students", data=enem)
sns.scatterplot(y="avg_score", x="number_of_students", s=100, label="Trustworthy",data=enem.query(f"number_of_students=={enem.number_of_students.max()}"))
sns.scatterplot(y="avg_score", x="number_of_students", s=100, label="Not so Much",data=enem.query(f"avg_score=={enem.avg_score.max()}"))
plt.title("ENEM Score by Number of Students in the School");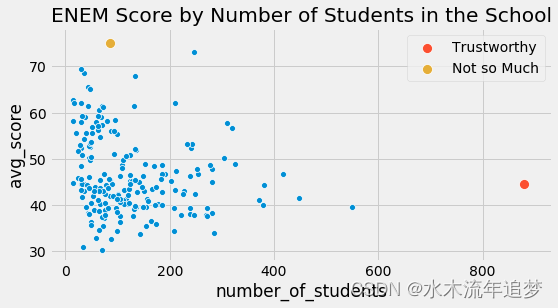

在上面的數據中，直觀上，左邊的點對我的模型的影響應該比右邊的點小。本質上，右邊的點實際上是許多其他數據點組合成一個。如果我們可以拆分它們并對未分組的數據進行線性回歸，那么它們對模型估計的貢獻確實比左側的未捆綁點要大得多。

這種同時具有一個低方差區域和另一個高方差區域的現象稱為異方差。簡而言之，異方差是指因變量的方差在各個特征變量的值域內方差不是恒定的。在上面的例子中，我們可以看到因變量方差隨著特征樣本大小的增加而減少。再舉一個我們有異方差的例子，如果你按年齡繪制工資，你會發現老年人的工資差異大于年輕人的工資差異。但是，到目前為止，方差不同的最常見原因是分組數據。

像上面這樣的分組數據在數據分析中非常常見。原因之一是保密。政府和公司不能泄露個人數據，因為這會違反他們必須遵守的數據隱私要求。如果他們需要將數據導出給外部研究人員，他們只能通過對數據進行分組的方式來完成。這樣，個人集合在一起，不再是唯一可識別的。

對我們來說幸運的是，回歸可以很好地處理這些類型的數據。要了解如何做，讓我們首先采用一些未分組的數據，例如我們在工資和教育方面的數據。在這些數據集中，每個工人對應一行數據，所以我們知道這個數據集中每個人的工資以及他或她有多少年的教育。

wage = pd.read_csv("./data/wage.csv")[["wage", "lhwage", "educ", "IQ"]]wage.head()

如果我們運行一個回歸模型來找出教育與對數小時工資的關系，我們會得到以下結果。

model_1 = smf.ols('lhwage ~ educ', data=wage).fit()
model_1.summary().tables[1]

現在，讓我們暫時假設這些數據有某種保密限制， 它的提供者無法提供個性化數據。 因此，我們請他將每個人按受教育年限分組，并只給我們平均對數小時工資和每個組中的人數。 這讓我們只剩下 10 個數據點。

group_wage = (wage.assign(count=1).groupby("educ").agg({"lhwage":"mean", "count":"count"}).reset_index())group_wage

不要怕！ 回歸不需要大數據就可以工作！ 我們可以做的是為我們的線性回歸模型提供權重。 這樣，相對樣本量稍小的群體，模型會更多地考慮樣本量更大的群體。 請注意我是如何用 smf.wls 替換 smf.ols 的，以獲得加權最小二乘法。 新方法會讓一切變得不同，雖然這點不容易被注意到。

model_2 = smf.wls('lhwage ~ educ', data=group_wage, weights=group_wage["count"]).fit()
model_2.summary().tables[1]

注意分組模型中 edu 的參數估計與未分組數據中的參數估計完全相同。 此外，即使只有 10 個數據點，我們也設法獲得了具有統計意義的系數。 那是因為，雖然我們的點數較少，但分組也大大降低了方差。 還要注意參數估計的標準誤差是變得大了一點，t 統計量也是如此。 那是因為丟失了一些關于方差的信息，所以我們必須更加保守。 一旦我們對數據進行分組，我們不知道每個組內的方差有多大。 將上面的結果與我們在下面的非加權模型中得到的結果進行比較。

model_3 = smf.ols('lhwage ~ educ', data=group_wage).fit()
model_3.summary().tables[1]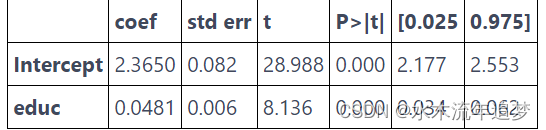

參數估計值相對較大。 這里發生的事情是回歸對所有點施加了相等的權重。 如果我們沿著分組點繪制模型，我們會看到非加權模型對左下角小點的重視程度高于應有的重視程度。 因此，該模型的回歸線具有更高的斜率。

sns.scatterplot(x="educ", y = "lhwage", size="count", legend=False, data=group_wage, sizes=(40, 400))
plt.plot(wage["educ"], model_2.predict(wage["educ"]), c="C1", label = "Weighted")
plt.plot(wage["educ"], model_3.predict(wage["educ"]), c="C2", label = "Non Weighted")
plt.xlabel("Years of Education")
plt.ylabel("Log Hourly Wage")
plt.legend();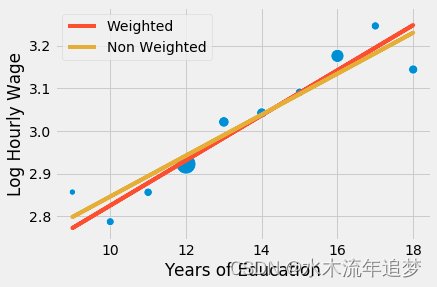

歸根結底，回歸就是這個奇妙的工具，可以處理單個數據或聚合數據，但在最后一種情況下您必須使用權重。 要使用加權回歸，您需要平均統計量。 不是總和，不是標準差，不是中位數，而是平均值！ 對于自變量和因變量都需要這么處理。 除了單一自變量回歸的情況外，分組數據的加權回歸結果與未分組數據的回歸結果不會完全匹配，但會非常相似。

我將用在分組數據模型中使用附加自變量的最后一個例子來結束。

group_wage = (wage.assign(count=1).groupby("educ").agg({"lhwage":"mean", "IQ":"mean", "count":"count"}).reset_index())model_4 = smf.wls('lhwage ~ educ + IQ', data=group_wage, weights=group_wage["count"]).fit()
print("Number of observations:", model_4.nobs)
model_4.summary().tables[1]
Number of observations: 10.0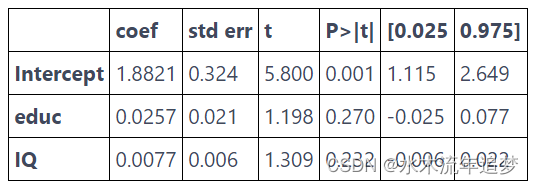

在此示例中，除了先前添加的教育年限之外，我們還包括 IQ 作為一個特征。運作機制幾乎相同：獲取均值并計數，回歸均值并將計數用作權重。