---

1.最長定差子序列

1.題目鏈接

• 最長定差子序列

---

2.算法原理詳解

• 思路：

  • 確定狀態表示 -> dp[i]的含義

    • 以i位置元素為結尾的所有子序列中，最長的等差子序列的長度

  • 推導狀態轉移方程
    

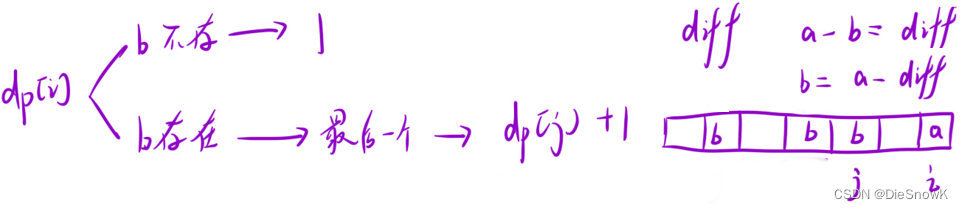
  • 優化：

    • 將元素 + dp[j]的值，綁定存放進哈希表中
      • 這樣就不用每次都從前向后遍歷原數組找值了
    • 直接在哈希表中，做動態規劃

  • 初始化：hash[arr[0]] = 1

  • 確定填表順序：從左往右

  • 確定返回值：整個dp表里的最大值

---

3.代碼實現

int longestSubsequence(vector<int>& arr, int difference) 
{unordered_map<int, int> hash; // <arr[i], dp[i]>hash[arr[0]] = 1;int ret = 0;for(int i = 1; i < arr.size(); i++){// 1.如果arr[j]不存在，那么arr[i]就會被初始化為1// 2.如果出現重復的值，那么后面出現的值會覆蓋掉前面的值hash[arr[i]] = hash[arr[i] - difference] + 1; ret = max(ret, hash[arr[i]]);}return ret;
}

---

2.最長的斐波那契子序列的長度

1.題目鏈接

• 最長的斐波那契子序列的長度

---

2.算法原理詳解

• 思路：

  • 確定狀態表示 -> dp[i]的含義

    • dp[i]：以i位置元素為結尾的所有的子序列中，最長的斐波那契子序列的長度 -> 無法正確表示狀態
      • 因為雖然可以找到i前一個值，但是卻無法得知此時它前一個數是什么，現在的規模到哪一步了
    • dp[i][j]：以i位置以及j位置的元素為結尾的所有的子序列中，最長的斐波那契子序列的長度(i < j)

  • 推導狀態轉移方程
    

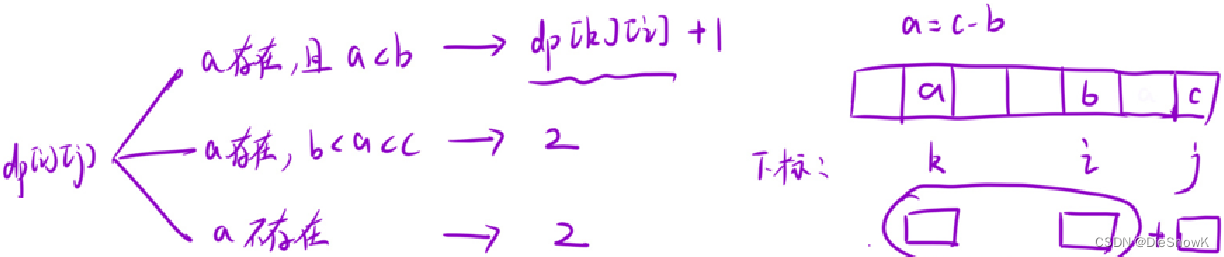
  • 優化：將數組中所有元素與它們的下標綁定，存在哈希表中，這樣有利于提升查找效率

  • 初始化：vector<vector<int>> dp(n, vector<int>(n, 2))

  • 確定填表順序：從上往下

  • 確定返回值：dp表里的最大值：ret < 3 ? 0 : ret

---

3.代碼實現

int lenLongestFibSubseq(vector<int>& arr) 
{int n = arr.size();// 優化unordered_map<int, int> hash; // <arr[i], i>for(int i = 0; i < n; i++){hash[arr[i]] = i;}vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;for(int j = 2; j < n; j++) // 固定第一個位置{for(int i = 1; i < j; i++) // 固定第二個位置{int a = arr[j] - arr[i];if(a < arr[i] && hash.count(a)){dp[i][j] = dp[hash[a]][i] + 1;ret = max(ret, dp[i][j]);}}}return ret < 3 ? 0 : ret;
}