目錄

11.2 ? 選擇排序

11.2.1 ? 算法特性

---

11.2 ? 選擇排序

選擇排序（selection sort）的工作原理非常簡單：開啟一個循環，每輪從未排序區間選擇最小的元素，將其放到已排序區間的末尾。

設數組的長度為?𝑛?，選擇排序的算法流程如圖 11-2 所示。

1. 初始狀態下，所有元素未排序，即未排序（索引）區間為?[0,𝑛?1]?。
2. 選取區間?[0,𝑛?1]?中的最小元素，將其與索引?0?處的元素交換。完成后，數組前 1 個元素已排序。
3. 選取區間?[1,𝑛?1]?中的最小元素，將其與索引?1?處的元素交換。完成后，數組前 2 個元素已排序。
4. 以此類推。經過?𝑛?1?輪選擇與交換后，數組前?𝑛?1?個元素已排序。
5. 僅剩的一個元素必定是最大元素，無須排序，因此數組排序完成。

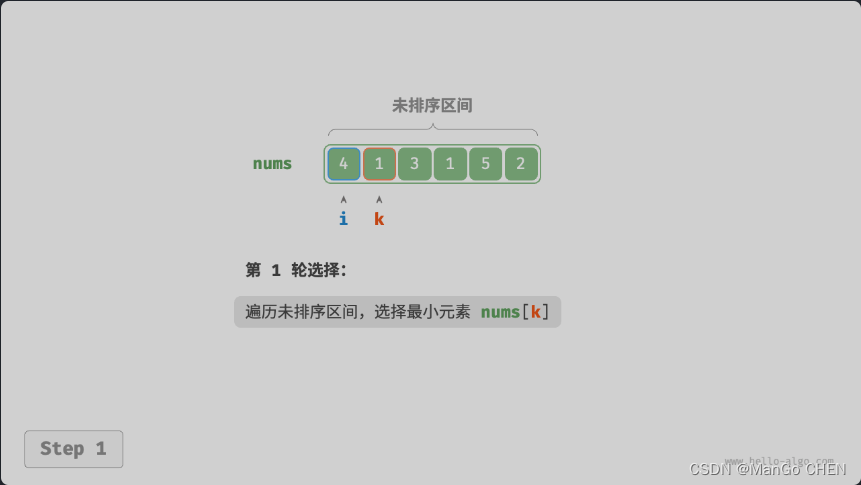
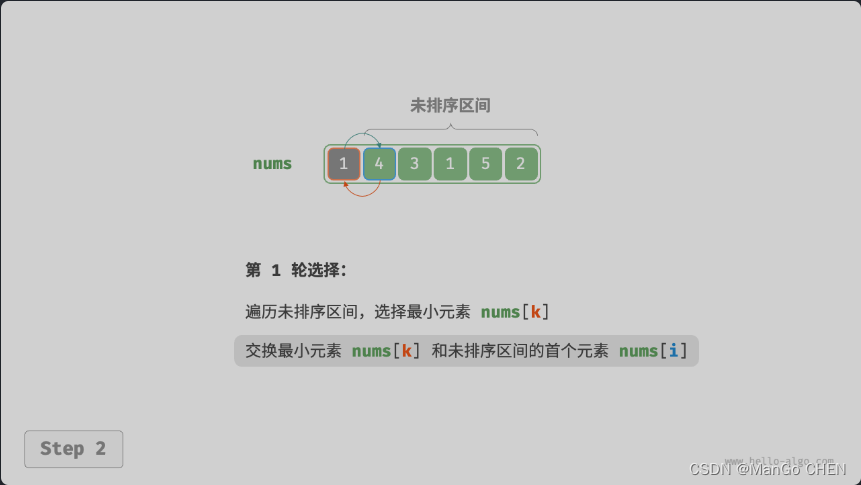
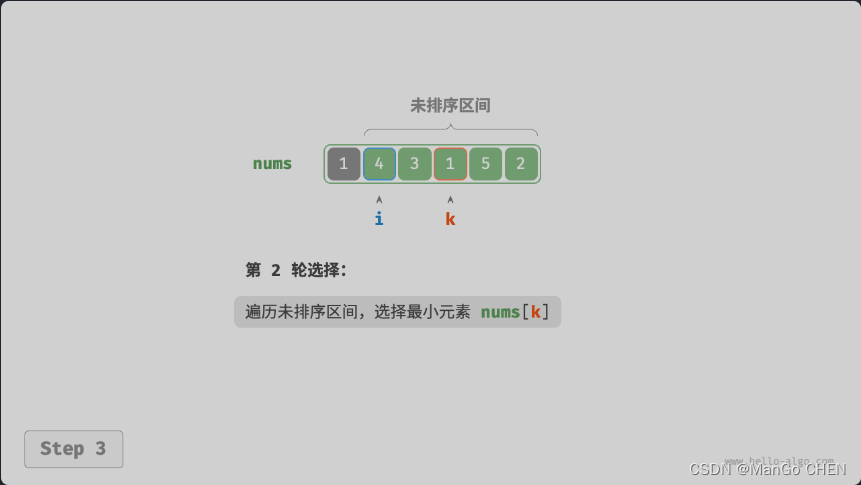
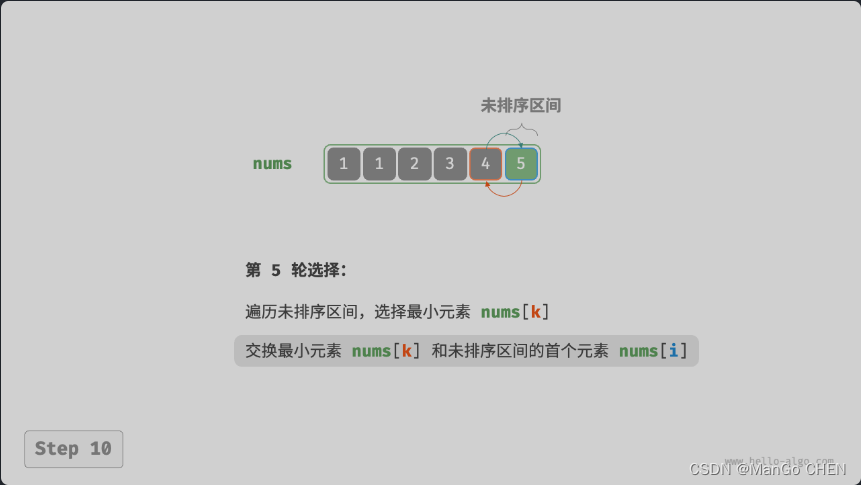
圖 11-2 ? 選擇排序步驟

在代碼中，我們用?𝑘?來記錄未排序區間內的最小元素：

selection_sort.c

/* 選擇排序 */
void selectionSort(int nums[], int n) {// 外循環：未排序區間為 [i, n-1]for (int i = 0; i < n - 1; i++) {// 內循環：找到未排序區間內的最小元素int k = i;for (int j = i + 1; j < n; j++) {if (nums[j] < nums[k])k = j; // 記錄最小元素的索引}// 將該最小元素與未排序區間的首個元素交換int temp = nums[i];nums[i] = nums[k];nums[k] = temp;}
}

11.2.1 ? 算法特性

• 時間復雜度為?𝑂(𝑛2)、非自適應排序：外循環共?𝑛?1?輪，第一輪的未排序區間長度為?𝑛?，最后一輪的未排序區間長度為?2?，即各輪外循環分別包含?𝑛、𝑛?1、…、3、2?輪內循環，求和為?(𝑛?1)(𝑛+2)2?。
• 空間復雜度為?𝑂(1)、原地排序：指針?𝑖?和?𝑗?使用常數大小的額外空間。
• 非穩定排序：如圖 11-3 所示，元素?nums[i]?有可能被交換至與其相等的元素的右邊，導致兩者的相對順序發生改變。

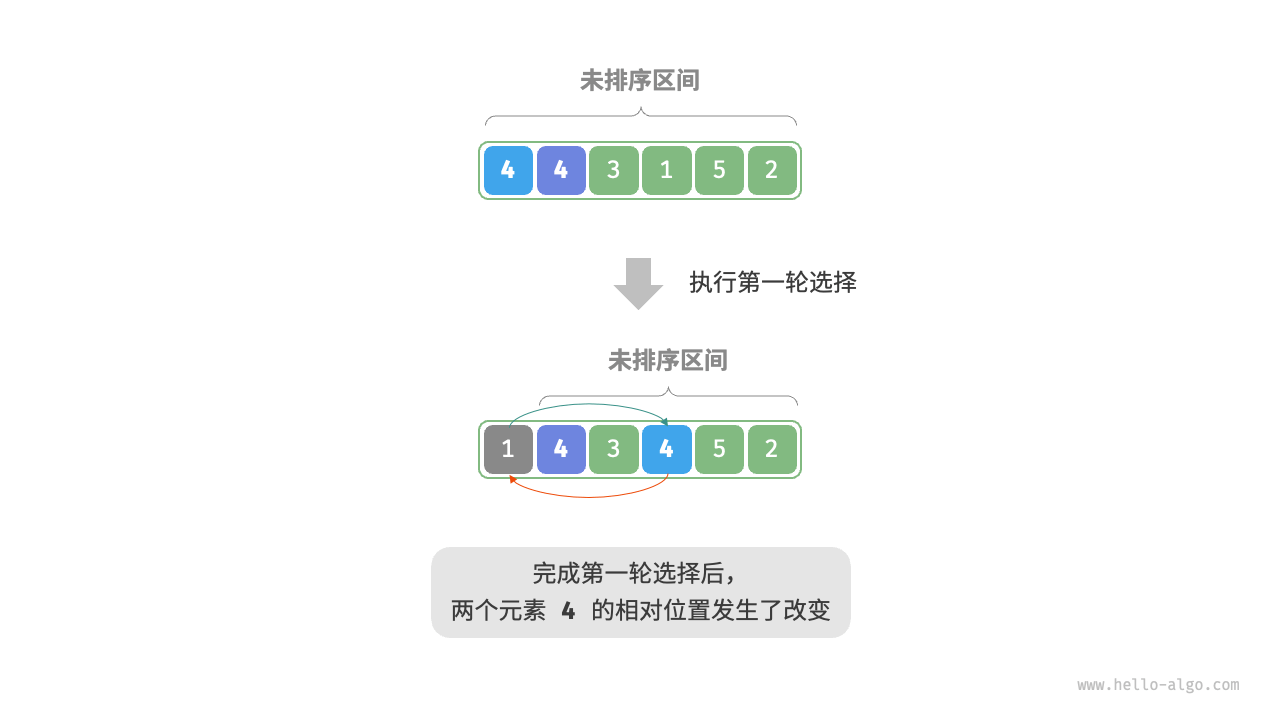
圖 11-3 ? 選擇排序非穩定示例