正則化
正則化是防止過擬合的一種方法,與線性回歸等算法配合使用。通過向損失函數增加懲罰項的方式對模型施加制約,有望提高模型的泛化能力。
概述
正則化是防止過擬合的方法,用于機器學習模型的訓練階段。過擬合是模型在驗證數據上產生的誤差比在訓練數據上產生的誤差(訓練誤差)大得多的現象。過擬合的一個原因是機器學習模型過于復雜。正則化可以降低模型的復雜度,有助于提高模型的泛化能力。
在詳細了解正則化的方法之前,我們先看一下使用了正則化的模型如何防止過擬合。這里使用的數據是圖 2-7 中的訓練數據(灰色的數據點)和驗證數據(黑色的數據點)。這些數據點是對函數 ![]() 添加了遵循高斯分布的隨機數而生成的。
添加了遵循高斯分布的隨機數而生成的。
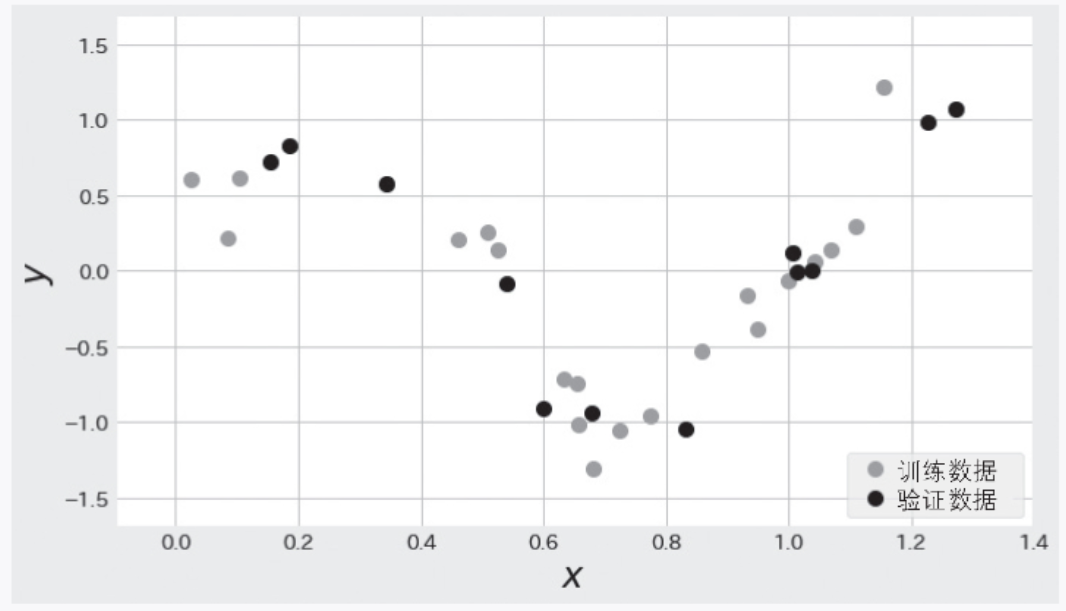
▲圖 2-7 使用 ![]() 加隨機數生成的數據
加隨機數生成的數據
下面嘗試用線性回歸對這份數據建模。不斷在線性回歸中加入一次項、二次項……觀察隨著多項式的次數越來越大,訓練誤差和驗證誤差會如何變化。
不同次數d的訓練結果如圖 2-8 所示。此時,使用均方誤差計算使誤差最小的學習參數wi。一次線性回歸函數是![]() ,因此圖形是直線;二次線性回歸函數是
,因此圖形是直線;二次線性回歸函數是 ![]() ,因此圖形是二次曲線;六次線性回歸函數是
,因此圖形是二次曲線;六次線性回歸函數是![]() ,它的圖形看上去是一個非常復雜的曲線。
,它的圖形看上去是一個非常復雜的曲線。
▲圖 2-8 不同次數的線性回歸的訓練結果(對于同樣的數據,復雜的模型會發生過擬合)
不同次數的訓練誤差和驗證誤差如表 2-5 所示。我們可以看出隨著函數次數的增加,訓練誤差漸漸變小了。如果只看訓練誤差,那么六次線性回歸的誤差 0.024 是最小的,但此時的驗證誤差是 3.472,比訓練誤差大了很多。六次線性回歸是一個復雜的模型,雖然它減小了訓練誤差,但是由于過擬合,它的泛化能力很低。
▼表 2-5 次數與訓練誤差、驗證誤差的關系
接下來看一下對線性回歸應用正則化后的結果,如圖 2-9 和表 2-6 所示。正則化可以通過向損失函數增加懲罰項的方式防止過擬合。從圖 2-9 可以看出,正則化抑制了模型的復雜度,次數增加后驗證誤差也被抑制,從而防止了過擬合的出現。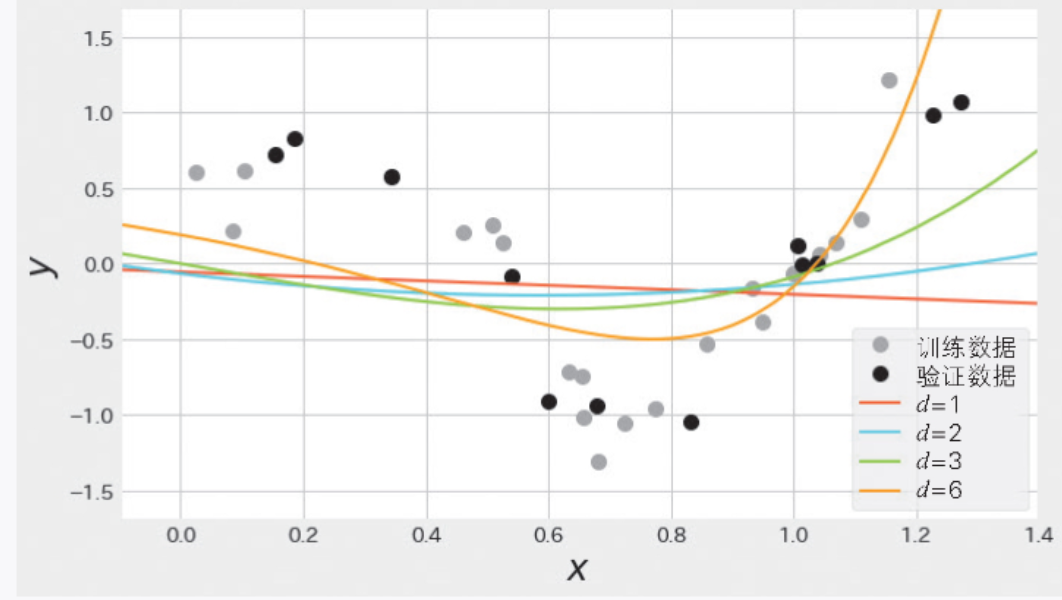
▲圖 2-9 對不同次數的線性回歸應用正則化后的訓練結果(模型的復雜度得到了抑制)
▼表 2-6 應用正則化后的次數與訓練誤差、驗證誤差的關系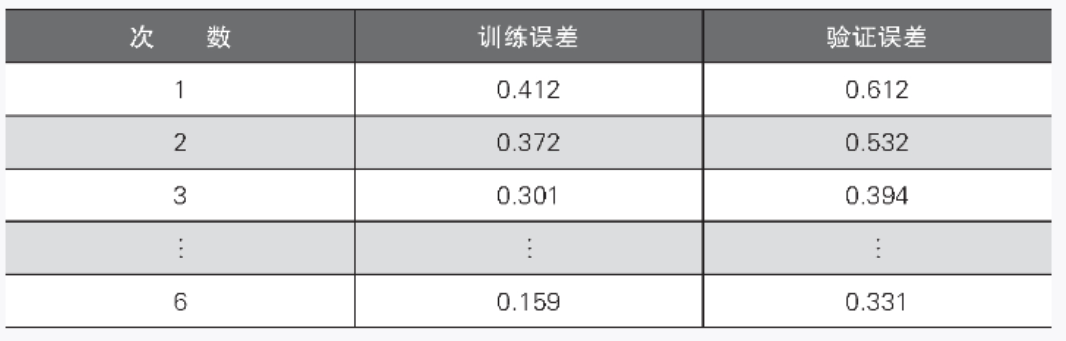
現在有許多正則化的方法。前面使用的回歸模型是被稱為嶺回歸(ridge regression)的具有代表性的回歸方法。下面的“算法說明”部分將介紹如何防止嶺回歸出現過擬合,從而提高它的泛化能力。
算法說明
在“概述”部分,我們了解了復雜模型的過擬合以及使用正則化防止過擬合的知識。復雜模型過擬合的一個原因是學習參數 wi的值太大(或太小)。表 2-7 列出了不同次數的線性回歸的學習參數。隨著次數的增加,學習參數的絕對值變大。
表 2-8 列出了使用正則化后的學習參數。使用正則化能夠抑制學習參數隨著次數增加而變大。
▼表 2-7 不同次數的學習參數
▼表 2-8 應用正則化后的不同次數的學習參數
為什么正則化可以抑制學習參數變大呢?這里以下面的嶺回歸的誤差函數為例進行說明。簡單起見,這里考慮對二次線性回歸應用正則化的情況:
等號右邊的第 1 項???????![]() 是線性回歸的損失函數。第 2 項
是線性回歸的損失函數。第 2 項 ![]() 被稱為懲罰項(或者正則化項),是學習參數的平方和的形式。一般來說,懲罰項中不包含截距。
被稱為懲罰項(或者正則化項),是學習參數的平方和的形式。一般來說,懲罰項中不包含截距。
另外,α是控制正則化強度的參數,α越大,對學習參數的抑制越強;α越小,對訓練數據過擬合的可能性越大。
下面思考嶺回歸的損失函數![]() 的最小化。
的最小化。
等號右邊的第 1 項![]() 其實是求使得與訓練數據 y 之間的誤差變小的任意 w0、w1、w2?的問題,右邊第 2 項(即懲罰項)是學習參數的平方和,因此學習參數的絕對值越大,損失函數整體的值就越大。由此可知,懲罰項具有“對絕對值大的學習參數給予損失變大的懲罰”的作用,這個作用可以抑制學習參數變大。
其實是求使得與訓練數據 y 之間的誤差變小的任意 w0、w1、w2?的問題,右邊第 2 項(即懲罰項)是學習參數的平方和,因此學習參數的絕對值越大,損失函數整體的值就越大。由此可知,懲罰項具有“對絕對值大的學習參數給予損失變大的懲罰”的作用,這個作用可以抑制學習參數變大。
示例代碼
下面是對 sin 函數進行嶺回歸建模時的示例代碼。代碼中使用 PolynomialFeatures 方法創建了六次多項式。
▼示例代碼
# 使用一個簡單的正弦函數和噪聲數據來訓練和測試一個 Ridge 回歸模型,并計算預測值與真實值之間的均方誤差。import numpy as np
from sklearn.preprocessing import PolynomialFeatures # PolynomialFeatures是scikit-learn庫中的一個特征轉換類,用于將輸入數據進行多項式特征擴展。它的主要參數是degree,表示多項式的次數。
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_errortrain_size = 20
test_size = 12# np.random.uniform(low=0, high=1.0, size=None) 是 NumPy 中的隨機數生成函數,用于生成在閉區間 [low, high] 內均勻分布的隨機浮點數。
# 生成一個訓練數據的數組,其中 low=0 表示數據的下限,high=1.2 表示數據的上限,size=train_size 表示生成的數組大小為 train_size。
train_X = np.random.uniform(low=0, high=1.2, size=train_size)
test_X = np.random.uniform(low=0.1, high=1.3, size=test_size)
# 生成一個訓練標簽的數組,其中 np.sin(train_X * 2 * np.pi) 表示一個正弦函數,np.random.normal(0, 0.2, train_size) 表示一個均值為 0,標準差為 0.2 的正態分布噪聲。
train_y = np.sin(train_X * 2 * np.pi) + np.random.normal(0, 0.2, train_size)
test_y = np.sin(test_X * 2 * np.pi) + np.random.normal(0, 0.2, test_size)poly = PolynomialFeatures(6) # 創建了一個次數為 6 的多項式特征轉換對象。
# fit_transform方法會遍歷輸入數據,并根據多項式特征轉換的規則對每個數據點進行擴展。對于訓練數據,通過train_X.reshape(train_size, 1)將其轉換為一維數組,以便與PolynomialFeatures的輸入要求匹配。同樣,對測試數據進行相同的轉換。
train_poly_X = poly.fit_transform(train_X.reshape(train_size, 1))
test_poly_X = poly.fit_transform(test_X.reshape(test_size, 1))# 創建一個嶺回歸模型,其中alpha=1.0是嶺回歸的正則化參數
model = Ridge(alpha=1.0)
# 使用訓練數據train_poly_X和標簽train_y對模型進行訓練。
model.fit(train_poly_X, train_y)
train_pred_y = model.predict(train_poly_X)
test_pred_y = model.predict(test_poly_X)print(mean_squared_error(train_pred_y, train_y))
print(mean_squared_error(test_pred_y, test_y))注:多項式特征轉換的目的是將原始數據轉換為更高維的數據,以便更好地表示數據的特征。通過添加更高次的多項式特征,可以捕捉數據中的非線性關系。
詳細說明
通過α控制正則化強度
下面來詳細看一下控制正則化強度的超參數α。圖 2-10 是使用不同的α 值時模型的可視化圖形。當 α 增大時,可以看出學習參數被抑制,圖形變得簡單。相反,當 α 變小時,對學習參數的絕對值變大的懲罰力度變緩,模型變復雜。另外,當α = 0?時,懲罰項始終為 0,因此等同于不使用正則化的線性回歸。一般來說,應一邊驗證誤差一邊對 α 進行調整,最終得到合適的 α。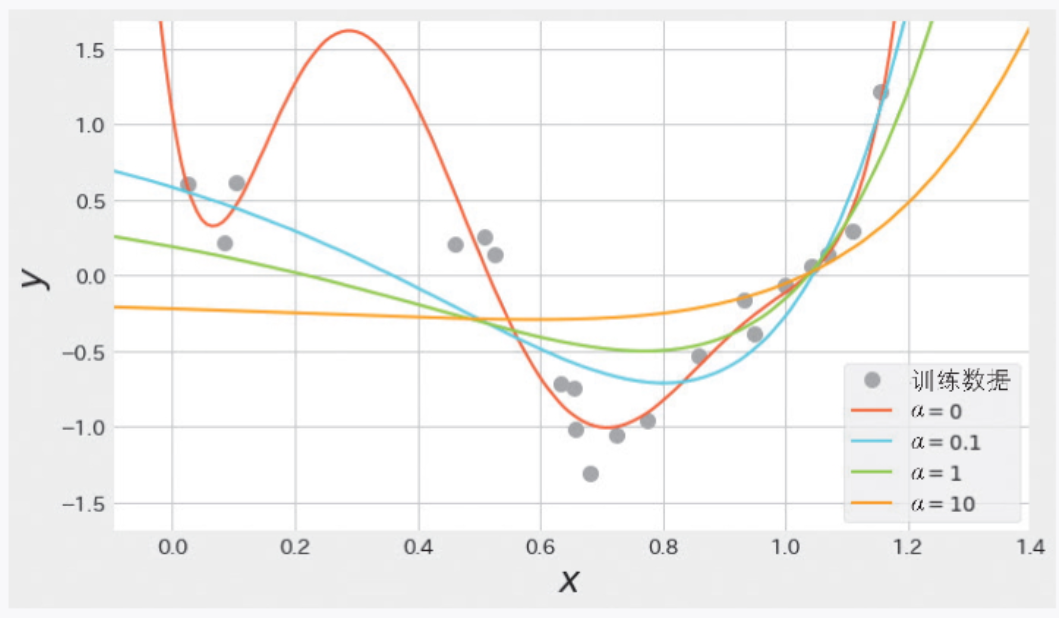
▲圖 2-10 α 變化時的嶺回歸
嶺回歸和 Lasso 回歸
前面介紹了作為正則化方法的嶺回歸。嶺回歸的誤差函數的懲罰項是學習參數的平方和的形式,通過將該懲罰項改為其他形式,可以實現不同特點的正則化。除了嶺回歸以外,還有一種具有代表性的正則化方法——Lasso 回歸。Lasso 回歸的誤差函數如下: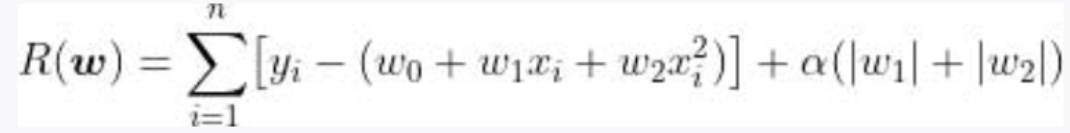
Lasso 回歸的懲罰項是學習參數的絕對值之和,這一點與嶺回歸不同。嶺回歸和 Lasso 回歸計算學習參數時的情況分別如圖 2-11a 和圖 2-11b 所示。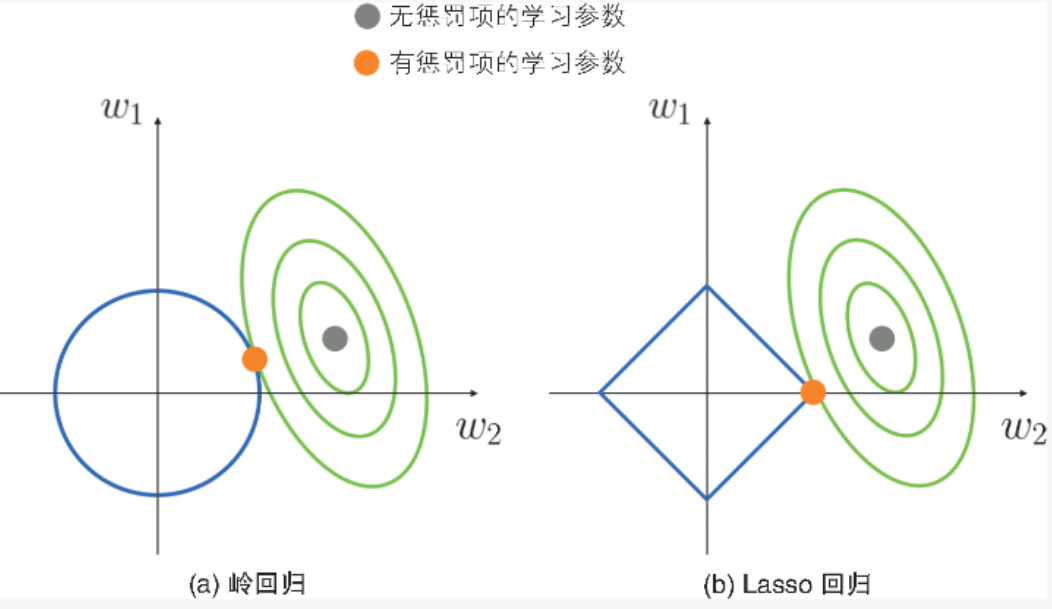
▲圖 2-11 計算學習參數時的示意圖
綠線是線性回歸的誤差函數,藍線是懲罰項的相關函數。嶺回歸的懲罰項是學習參數的平方和,所以其圖形是圖 2-11a 所示的圓形;Lasso 回歸的懲罰項是絕對值的和,所以其圖形是圖 2-11b 所示的四邊形。原來的函數(線性回歸的誤差函數)與這些函數的交點就是帶有正則化項的誤差函數的最佳解。可以看出,在加入懲罰項后,圖 2-11a 的嶺回歸的學習參數得到了抑制。圖 2-11b 的 Lasso 回歸的情況與嶺回歸相似,學習參數同樣被抑制,但學習參數 w2?變為了 0。
Lasso 回歸計算的是函數與這種四邊形函數的交點,因此具有學習參數容易變為 0 的特點。利用這個特點,我們可以使用學習參數不為 0 的特征來構建模型,從而達到利用 Lasso 回歸選擇特征的效果。這樣不僅能提高模型的泛化能力,還能使模型的解釋變容易。
———————————————————————————————————————————
文章來源:書籍《圖解機器學習算法》
作者:秋庭伸也 杉山阿圣 寺田學
出版社:人民郵電出版社
ISBN:9787115563569
本篇文章僅用于學習和研究目的,不會用于任何商業用途。引用書籍《圖解機器學習算法》的內容旨在分享知識和啟發思考,尊重原著作者宮崎修一和石田保輝的知識產權。如有侵權或者版權糾紛,請及時聯系作者。
———————————————————————————————————————————
?



















)