😸二叉搜索樹的概念

二叉搜索樹又名二叉排序樹，一般具有以下性質：

1. 若它的左子樹不為空，則左子樹上所有節點的值都小于根節點的值
2. 若它的右子樹不為空，則右子樹上所有節點的值都大于根節點的值
3. 它的左右子樹也分別為二叉搜索樹

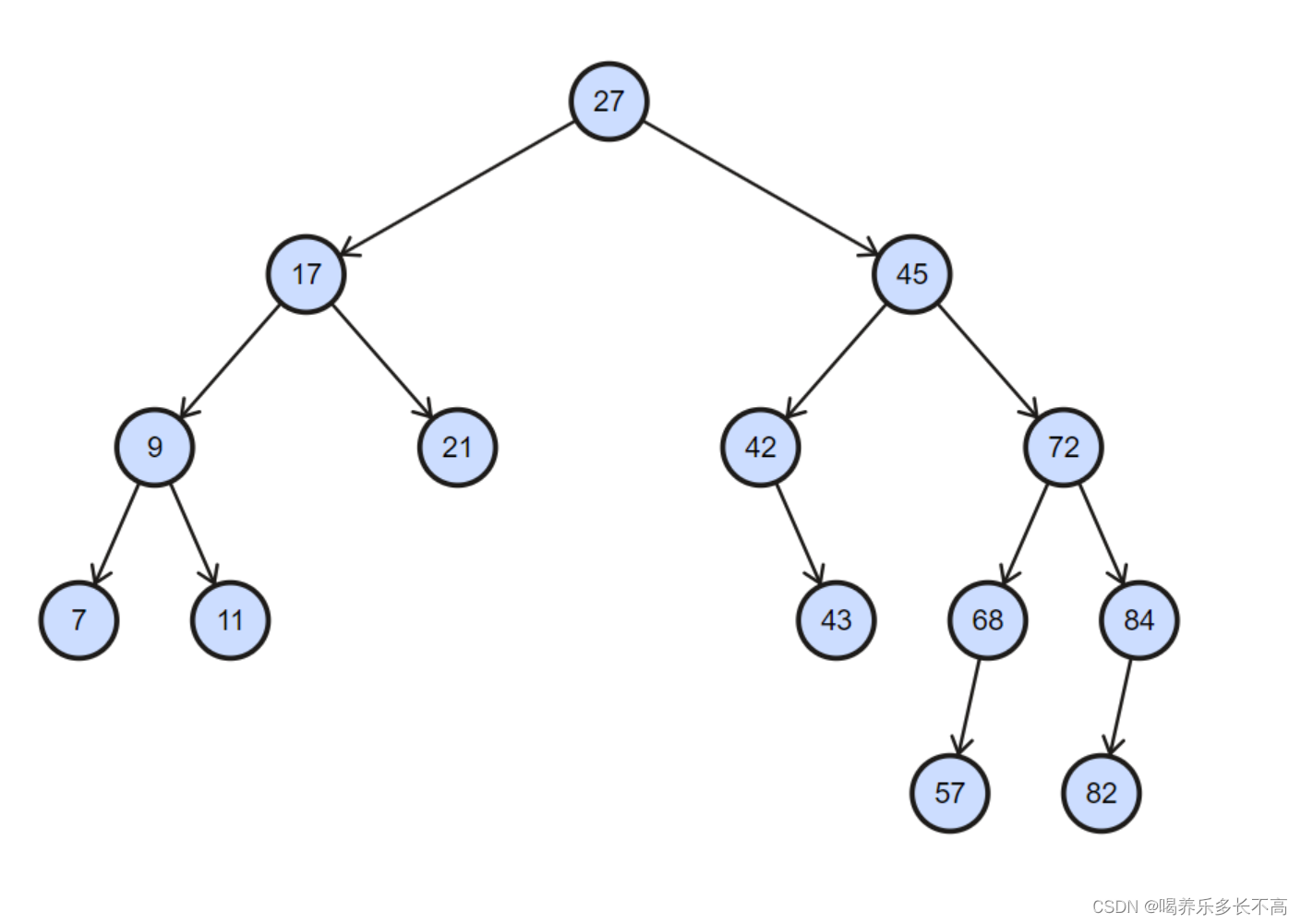將其具現為一個圖就是這樣?

🐭二叉搜索樹的查找

我們可以根據二叉搜索樹的特性，它的每一個結點的左子樹比根小右子樹比根大來進行快速查找，當一個數比根結點小就往根結點的左邊找，比根結點大就往右邊找，每次都可以將搜索范圍縮小一半，最多查找h(樹的高度)次，一個相對平衡的二叉樹搜索樹的時間復雜度大概為O(logN)，為什么要說相對平衡呢?🤔因為在極端情況下，假如一棵二叉樹只有右子樹，那么他就會變成一個鏈表，這時他的復雜度就會變成O(logN)。所以在實際使用中，要注意維護二叉搜索樹的平衡性(形狀)，因此在二叉搜索樹的基礎上，就誕生出了一些更具平衡性的樹如，紅黑樹，AVL樹。

🐭二叉搜索樹的排序

因為二叉搜索樹的每一棵子樹都滿足左子樹 < 根 < 右子樹，所以我們可以進行中序遍歷，這樣就可以得到一個升序序列了，一個相對平衡的二叉樹搜索樹的時間復雜度大概為O(NlogN)

😸二叉搜索樹的實現

🐱二叉搜索樹的創建

具體方法和創建一棵二叉樹一樣，每棵樹都要有左右子樹，然后創建一個初始的根結點

🐱二叉搜索樹的查找

為了方便我們先寫一個判空方法😋

🐭思路：

1. 從根節點開始一直向下遍歷
2. 當目標值大于當前結點的值，就往右子樹中繼續搜索
3. 當目標值小于當前結點的值，就往左子樹中繼續搜索
4. 當目標值剛好等于當前結點值，直接返回true表示已經找到
5. 當遍歷到最后依然每找到則返回false表示沒找到

這里我來畫圖舉個例子：

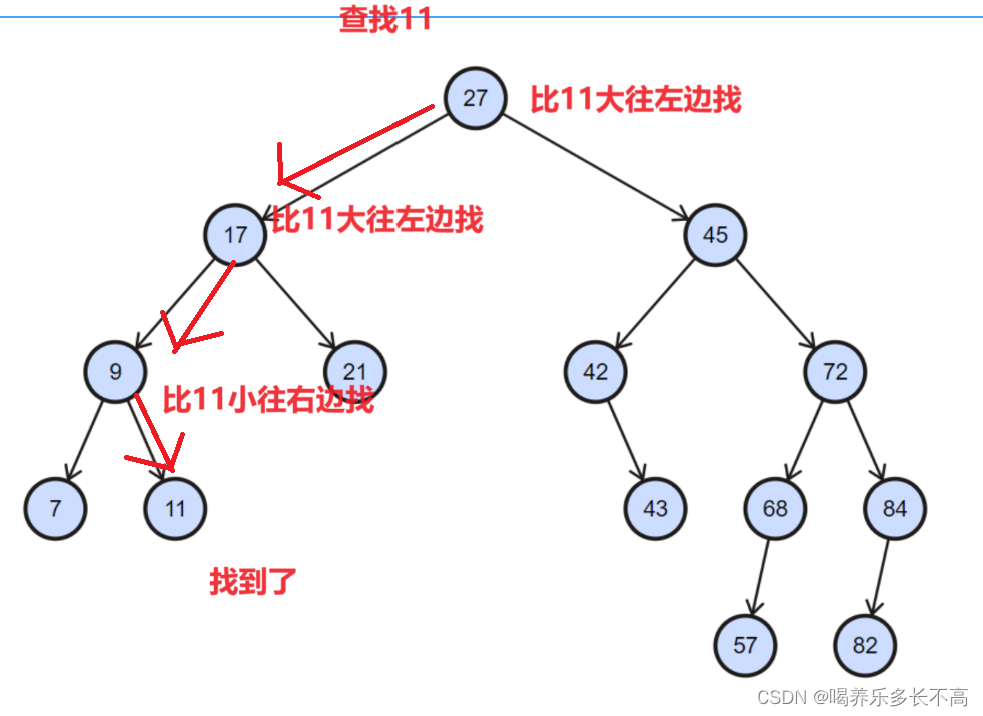
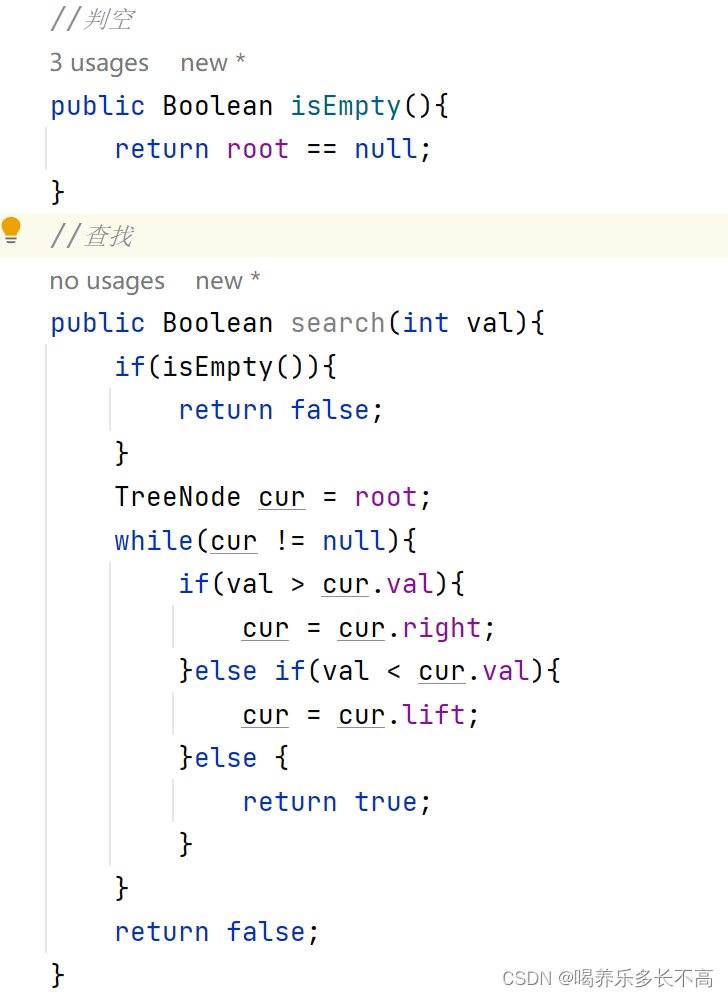
🐱二叉搜索樹的插入

🐭思路：

二叉搜索樹的插入只能插到葉子結點上，而且不能插入相同的結點

首先需要先判斷樹是否為空

樹為空：

😊即根結點為空，直接插入就行

樹不為空：

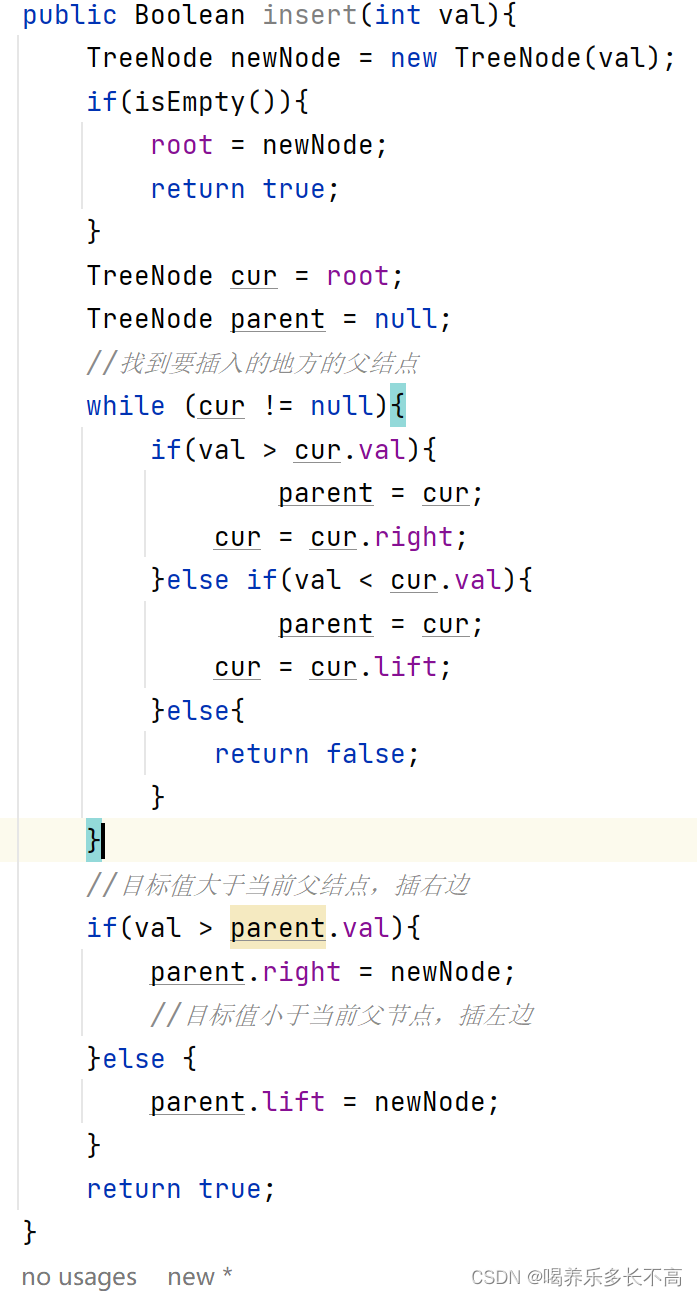
😊因為二叉樹不像鏈表，直接遍歷到最后一個結點然后將新結點連在最后一個結點的后就行，二叉搜索樹可能要插在左邊還可能插在右邊，所以不能像鏈表那樣直接cur.next != null找到最后一個結點，我們要先定義一個父節點，用來標記要插到的葉子結點的父節點，先找到這個父節點然后在判斷，要插入的值和這個父節點的大小以判斷是插在左邊還是右邊。

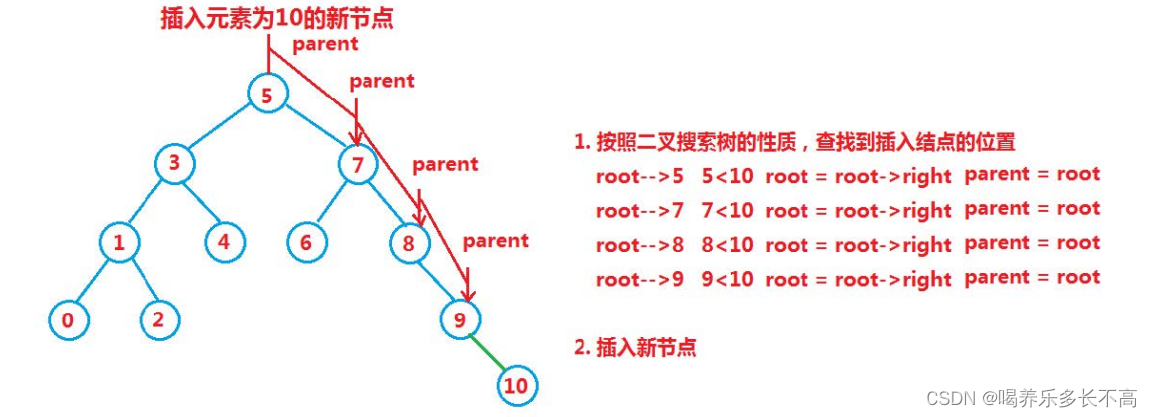
🐱🐱二叉搜素樹的刪除(難點)

🐭思路：

首先我們要先找到要刪除的結點，并且還有記住他的父節點，方法和剛剛寫的插入類似，大的往右找小的往左找，當找到后對結點進行刪除，那么要怎么刪除呢🧐？因為比較復雜，需要單獨寫一個方法😋。

//parent是待刪除的結點的父結點，cur是要刪除的結點

因為這是一個二叉樹刪除之后不能破壞它的結構所以不能像線性表那樣直接刪除，要分幾種情況：

🐭要刪除的結點左邊為空cur.left==null

1.cur是根結點，則直接讓root = cur.right

要刪除的結點左邊為空，并且是根結點所以直接讓根結點等于其右子樹就行

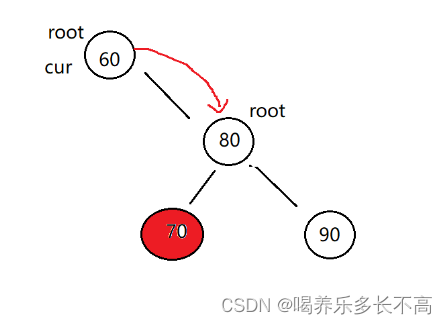
2. cur 不是 root，cur 是 parent.left，則 parent.left = cur.right

如圖，因為要刪除的結點沒有左子樹，并且是父節點的左子樹，所以直接讓父節點的左邊連上cur的右邊

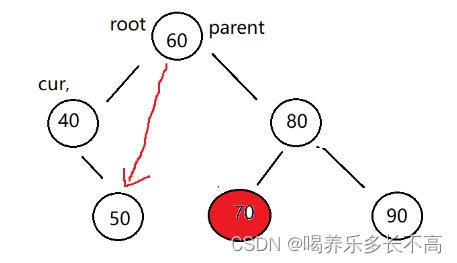
3. cur 不是 root，cur 是 parent.right，則 parent.right = cur.right

和上一個類似，因為要刪除的結點沒有左子樹，并且是父節點的右子樹，所以直接讓父節點的右邊連上cur的右邊

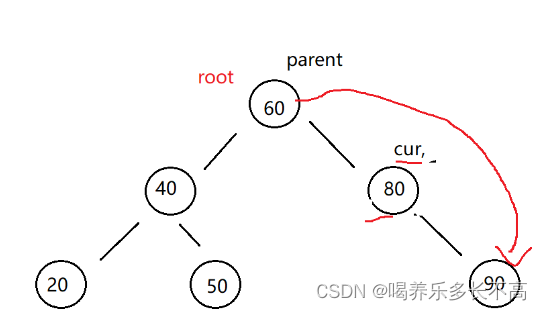
🐭要刪除的結點右邊為空cur.right == null

1. cur 是 root，則 root = cur.left

因為要刪除的結點右邊為空，并且是根結點所以直接讓根結點等于根結點的左子樹

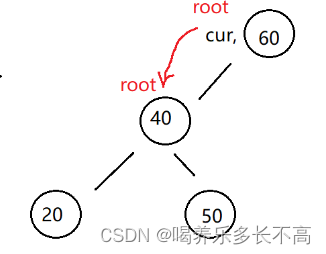
2. cur 不是 root，cur 是 parent.left，則 parent.left = cur.left

因為cur是父節點的左邊，并且cur沒有右子樹，所以直接讓父節點的左邊，連cur的左邊

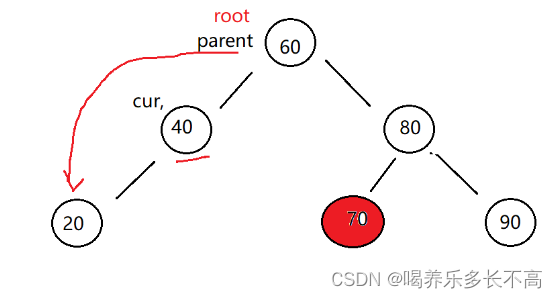
3. cur 不是 root，cur 是 parent.right，則 parent.right = cur.left

因為cur是父節點的右邊，并且沒有右子樹，所以直接讓父節點的右邊連cur的左邊

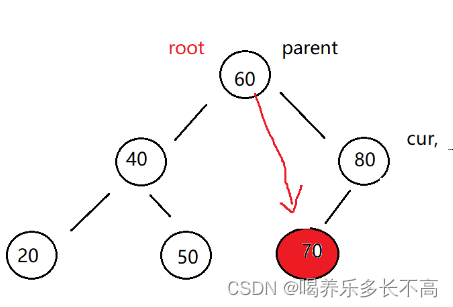
🐭要刪除的結點左右都為空cur.left != null && cur.right != null

這種情況利用上面的方法依然可以實現，比如cur在父節點的右邊，因為cur沒有子樹，所以不管父節點連cur的左邊還是右邊(左右都為null)都可以完成刪除,cue在父節點左邊也是一樣的，所以這部分內容利用上面的代碼也能實現

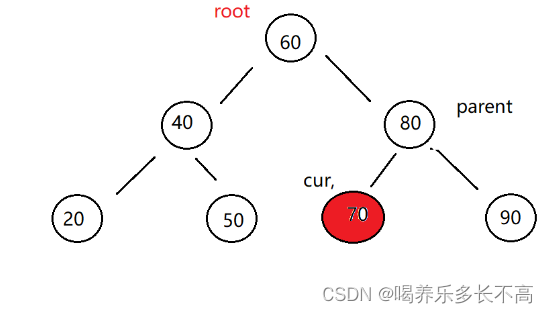
以上我們討論的是要刪除的結點右空的子樹的情況，那么接下來我們要討論沒有子樹的情況即：

🐭要刪除的結點左右都不為空

當cur左右結點都不為空時就會比較麻煩，我們的老招式就不管用了😣😟比如這樣：

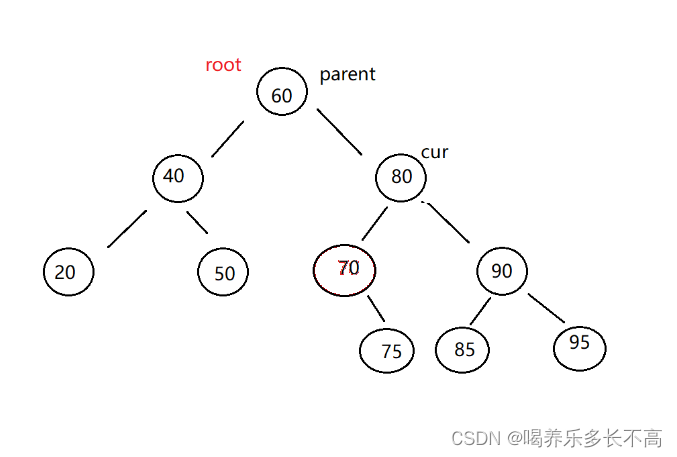
這該讓父節點怎么連？🤔好像不管怎么連都會破壞樹的結構🧐那么索性就不連了，因為當樹的結構比較復雜時這樣很容易就會破壞樹的結構，那么就不刪了嗎🧐當然不是，只是用的方法不是刪除，而是替代。如果我用一個合適的數去把我要刪除的這個數給替代掉，然后再將這個數原來所在的結點刪除，不就間接的完成了刪除而且不會破壞樹的結構了嗎😉，用的這個方法也可以叫做尋找替罪羊。

思路：

既然我們在替代后，還要刪除掉原來結點那么我們找的替罪羊(用來覆蓋cur的結點)必須容易刪除要不然就沒有意義，所以替罪羊至少具有兩點，1結點左右子樹必須有空的，2大小必須合適，要滿足二叉搜索樹左邊比結點小右邊比結點大的特性。

左右子樹必有空，只需要向下查找總能找到，那么我們現在要思考的是怎么找到大小合適的結點？

根據二叉搜索樹的的特性我們有兩種方法可以找到

• 在cur的左邊找最大值
• 在cur的右邊找最小值

這里我就使用在cur的右邊找最小值來演示，因為cur的右子樹都是比cur大的數，所以我們就要在其右子樹中找到比cur.right小的數就行，那么只需要找cur.right的左子樹不就好了😉，既比cur大(因為在cur右邊),又比cur.right小(因為在cur左邊)

所以根據上面的分析我們知道了我們要找的結點是cur.right的左子樹，并且這個替罪羊結點有空的子樹，如果能找到，這個空的結點必然是左子樹(如果左子樹還有結點證明還可以向下查找)最后用這個結點覆蓋掉cur，再刪掉就行😉

//在cur的左邊找最大值，同理找cur.left的右子樹如果能找到，他的右子樹必然是空的

//如果替罪羊結點就是cur.right就不能再往左邊找了，因為這時左邊已經為空了，所以要單獨判斷一下

😸性能分析

二叉搜索樹插入和刪除操作都必須先查找，查找效率代表了二叉搜索樹中各個操作的性能。 對有n個結點的二叉搜索樹，若每個元素查找的概率相等，則二叉搜索樹平均查找長度是結點在二叉搜索樹的深度 的函數，即結點越深，則比較次數越多。

最優情況下，二叉搜索樹為完全二叉樹，其平均比較次數為：logN

最差情況下，二叉搜索樹退化為單支樹，其平均比較次數為：N/2

🐭到這里我們就聊完了二叉搜索樹，如果你有什么不懂或者其他見解歡迎在下方評論或者私信博主，也可以希望多多支持一下博主！！！🥰🥰，我們下一個篇章聊一聊java中的map和set😸