概述
瀏覽器的前進、后退功能,你肯定很熟悉吧?
當依次訪問完一串頁面 a-b-c 之后,點擊瀏覽器的后退按鈕,就可以查看之前瀏覽過的頁面 b 和 a。當后退到頁面 a,點擊前進按鈕,就可以重新查看頁面 b 和 c。但是,如果你后退到頁面 b 后,點擊新的頁面 d,那就無法再通過前進、后退功能查看頁面 c 了。
假設你是瀏覽器的開發工程師,你會如何實現這個功能呢?
這就要用到本章講的 “棧” 這種數據結構了。
如何理解 “棧”?
關于 “棧”,有一個非常貼切的例子,就是一摞疊在一起的盤子。我們平時放盤子時,都是從下往上一個一個的放;取的時候,也是從上往下一個一個地依次取,不能從中間任意抽出。后進者先出,先進者后出,這就是典型的 “棧” 結構。
從棧的操作特性上來看,棧是一種 “操作受限” 的線性表,只允許在一端插入和刪除數據。
第一次接觸這種數據類型時,我對它存在的意義產生了很大的疑惑。因為我覺得,相比數組和鏈表,棧給我的只有限制,并沒有任何優勢。那我直接使用數組或鏈表不就好了嗎?為什么還要用這個 “操作受限” 的 “棧” 呢?
事實上,從功能上來說,數組或鏈表確實可以替代棧,但你要知道,特定的數據結構是對特定場景的抽象,而且,數組或鏈表暴露了太多的接口,操作上的確靈活,但使用時就比較不可控,自然也就容易出錯。
當某個數據集合只涉及在一端插入和刪除數據,并且滿足后進先出、先進后出的特性,這是應該首選 “棧” 這種數據結構。
如何實現一個 “棧”?
從剛才棧的定義里,我們可以看出,棧主要包含兩個操作,入棧和出棧,也就是在棧頂插入一個數據和從棧頂刪除一個數據。理解了棧的定義后,我們來看下如何用代碼實現一個棧。
實際上,棧既可以用數組來實現,也可以用鏈表來實現。
- 用數組實現的棧,我們叫做順序棧。
- 用鏈表實現的棧,我們叫做鏈式棧。
這里實現一個基于數組的順序棧。
這段代碼使用 Java 來實現,但不涉及任何高級語法,并且用了中文做了詳細的注釋。
public class ArrayStack {private String[] items; // 數組private int count; // 棧中元素個數private int n; // 棧大小public ArrayStack(int n) {this.items = new String[n];this.count = 0;this.n = n;}// 入棧操作public boolean push(String item) {if (count == n) {// 數組空間不夠了,直接返回false,入棧失敗return false;}items[count] = item;count++;return true;}// 出棧操作public String pop() {if (count == 0) {// 棧為空,直接返回nullreturn null;}// 返回下標為count-1的數組元素,并且棧中元素個數減1String temp = items[count - 1];count--;return temp;}
}
了解了定義和基本操作,那它的操作時間、框架復雜度時多少呢?
不管是順序棧還是鏈式棧,存儲數據只需要一個大小為 n 的數組就夠了。在入棧和出棧的過程中,只需要一兩個臨時變量存儲空間,所以空間復雜度時 O ( 1 ) O(1) O(1)。
注意,這里存儲數據需要一個大小為 n 的數組,并不是說空間復雜度就是 O ( n ) O(n) O(n)。因為,這 n 個空間是必須的,無法省掉。所以我們說空間復雜度的時候,是除了原本的數據存儲空間外,算法運行還需要額外的存儲空間。
框架復雜度分析是不是很簡單?時間復雜度也不難。不管是順序棧還是鏈式棧,入棧、出棧只涉及棧頂個人數據的操作,所以時間復雜度都是 O ( 1 ) O(1) O(1)。
支持動態擴容的順序棧
剛才那個基于數組實現的棧,是一個固定大小的棧,也就是說,在初始化棧時需要實現制定棧的大小。當棧滿之后,就無法再往棧里添加數據了。盡管鏈式棧的大小不受限,但要存儲 next 指針,內存消耗相對較多。那我們如何基于數組實現一個可以支持動態擴容的棧呢?
還記得在數組那篇文章,是如何來支持一個支持動態擴容的數組嗎?當數組空間不夠時,我們就重新申請一塊更大的內存,將原來數組中的數據統統拷貝過去。這樣就實現了一個支持動態擴容的數組。
所以,如果要實現一個支持動態擴容的棧,我們只需要底層依賴一個支持動態擴容的數組就可以了。當棧滿了之后,我們就申請一個更大的數組,將原來的數據搬移到新數組中。
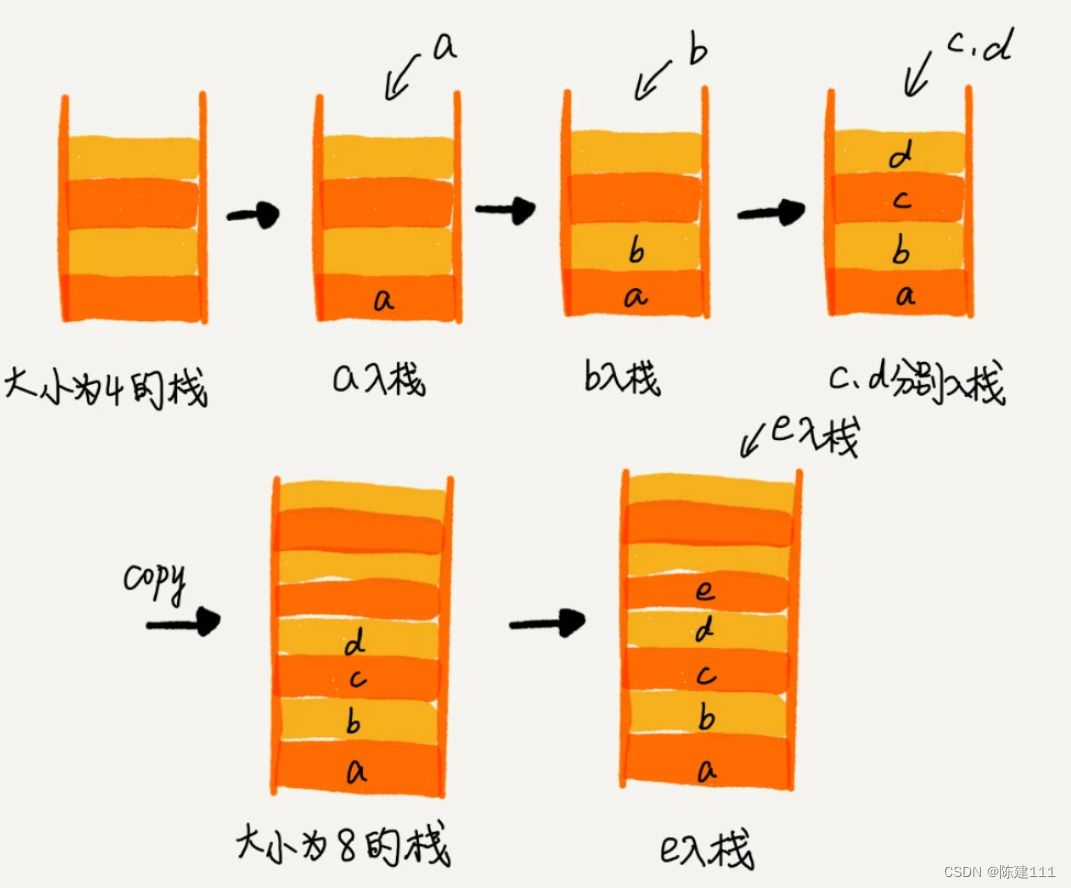
實際上,支持動態擴容的順序棧,我們平時開發中并不常用到。講這個的目的,主要還是希望帶你練習一下前面將的復雜度分析方法。
你不用死記硬背入棧、出棧的時間復雜度,你需要掌握的是分析方法。能夠自己分析才算是真正掌握了。現在就帶你一起分析一下支持動態擴容的順序棧的入棧、出棧的時間復雜度。
對于出棧操作來說,我們不會涉及內存的重新申請和數據搬移,所以出棧的時間復雜度還是 O ( 1 ) O(1) O(1)。但是對于入棧來說,當占用有空閑空間時,入棧操作的時間復雜度是 O ( 1 ) O(1) O(1)。但當空間不夠時,就需要申請內存和數據搬移,所以時間復雜度編程了 O ( n ) O(n) O(n)。
也就是說,對于入棧操作,最好情況時間復雜度是 O ( 1 ) O(1) O(1),最壞情況時間復雜度是 O ( n ) O(n) O(n)。那平均情況下的時間復雜度又是多少呢?還記得我們在復雜度那篇文章中講的攤還分析法嗎?這個入棧操作的平均時間復雜度可以用攤還分析法來分析。正好也借此再回顧一下攤還分析法。
為了分析的方便,我們需要預先做一些假設和定義:
- 棧空間不夠時,我們重新申請一個原來大小兩倍的數組;
- 為了簡化分析,假設只有入棧操作沒有出棧操作;
- 定義不涉及內存搬移的入棧操作為
simple-push,時間復雜度為 O ( 1 ) O(1) O(1)。
如果當前棧大小為 k,并且已滿,當再有新的數據要入棧時,就需要重新申請 2 倍大小的內存,并且做 k 個數據的搬移操作,然后再入棧。
- 我們將
k個數據的搬移操作,均攤到前面 k 次的simple-push操作。 - 均攤后,每個入棧只需要一次
simple-push操作和 一次搬移操作。 - 也就是說,均攤后,入棧操作的均攤時間復雜度就為 O ( 1 ) O(1) O(1)。
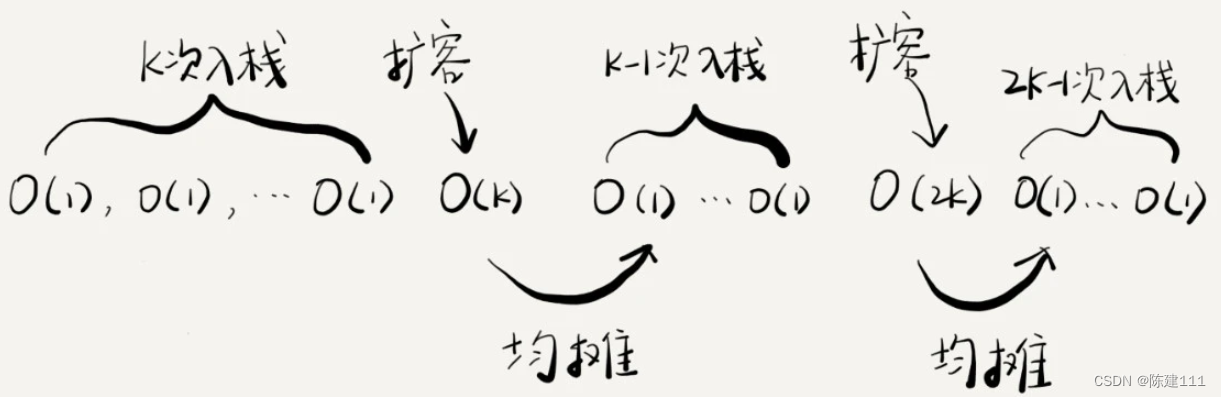
通過這個例子的實戰分析,也印制了前面講的,均攤時間復雜度一般都等于最好情況時間復雜度。因為在大部分情況下,入棧的操作時間復雜度都是 O ( 1 ) O(1) O(1),只有在個別時刻才會退化為 O ( n ) O(n) O(n),所以把好是多的入棧操作均攤到其他入棧操作上,平均情況下的耗時就接近 O ( 1 ) O(1) O(1)。
棧在函數調用中的應用
接下來在看棧的另一個常見的應用場景,編譯器如何利用棧來實現表達式求值。
為了方便解釋,我們將算術表達式簡化為只包含加減乘除四則運算,比如:34+13*9+44-12/3。對于這個四則運算,人腦可以很快求接觸答案,但是對于計算機來說,理解這個表達式本身就是個挺難得事兒。如果換作你,讓你來實現這樣一個表達式求值的功能,你會怎么做?
實際上,編譯器就是通過兩個棧來實現的。其中一個是保存操作數的棧,另一個是保存運算符的棧。我們從左向右遍歷表達式:
- 當遇到數字,我們就直接壓入操作數棧;
- 當遇到運算符,就與運算符棧的棧頂元素進行比較。
- 如果運算符 比 運算符棧頂元素的優先級高,就將當前的運算符壓入棧;
- 如果運算符 比 運算符棧頂元素的優先級低或者相同,從運算符中取棧頂運算符,從操作數棧的棧頂取 2 個操作數,然后進行計算,再把計算的記過壓入操作數棧,繼續比較。
我們將 3+5*8-6 這個表達式的計算過程畫了一張圖,你可以 結合圖來理解上面的計算過程。
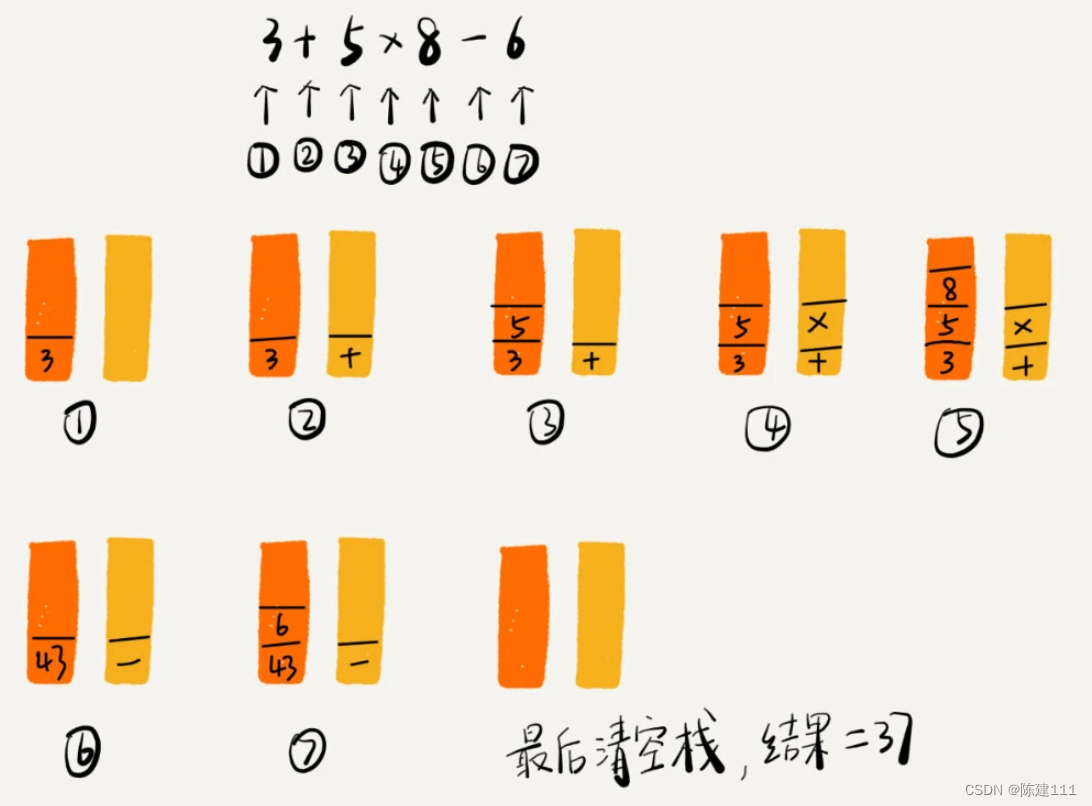
棧在括號匹配中的應用
除了用棧來實現表達式求值,還可以借助棧來檢查表達式中的括號匹配。
假設表達式中只包含三種括號,圓括號 ()、花括號 {} 和方括號 [],并且它們可以任意嵌套。比如 {[]()[{}]} 或 [{()}([])] 等都為合法格式,而 {[}()] 或 [({)] 問哦不合法格式。那我現在給你一個包含三種括號的表達式字符串,如何檢查它們是否合法呢?
這里也可以使用棧來解決。用棧來保存未匹配的左括號,從左到右一次掃描字符串。當掃描到左括號時,將其壓入棧中;當掃描到有括號時,從棧頂取出一個左括號。如果能夠匹配,比如 ( 跟 ) 匹配,[ 跟 ] 匹配,{ 跟 } 匹配,則繼續掃描剩下的字符串。如果掃描過程中,遇到不能匹配的右括號,或者棧中沒有數據,則說明為非法格式。
當所有的括號都掃描完成之后,如果棧為空,則說明字符串為合法字符串;否則,說明有未匹配的左括號,為非法格式。
如何實現瀏覽器的前進、后退功能?
其實,用兩個棧就可以完美解決。
我們使用兩個棧,X 和 Y,我們把首次瀏覽的頁面壓入棧 X,當點擊后退按鈕時,再一次從棧 X 中出棧,并將出棧的數據依次放入棧 Y。當我們點擊前進按鈕時,依次從棧 Y 中取出數據,放入棧 X。當 X 中沒有數據時,那就說明沒有頁面可以后退瀏覽了。當棧 Y 中沒有數據,那就說明沒有頁面可以點擊前進按鈕瀏覽了。
比如,你順序查看了 a,b,c 三個頁面,我們依次把 a,b,c 壓入棧 X,這個時候,兩個棧的數據就是這個樣子的。
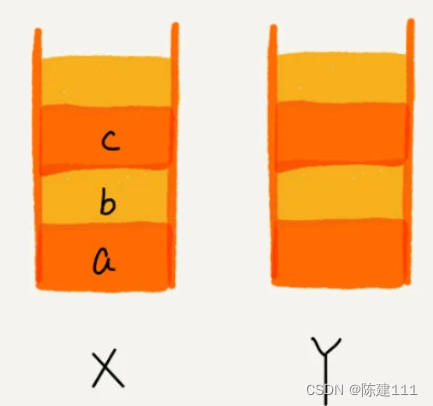
當你通過后退按鈕,從頁面 c 退到頁面 a 之后,我們就一次把 c 和 b 從棧 X 中取出,并依次放入棧 Y。這個時候數據就是這樣的。
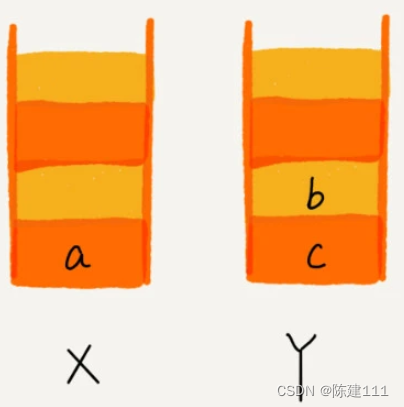
這個時候,如果你又想看頁面 b,于是你點擊了前進按鈕回到頁面 b,我們就再把 b 從棧 Y 出棧,放入棧 X。
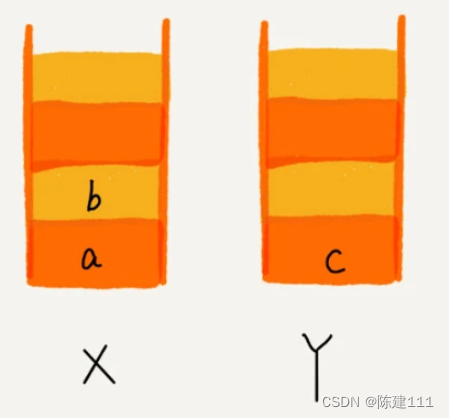
這個時候,你通過頁面 b 跳轉到新的頁面 d,頁面 c 就無法再通過前進、后退按鈕重復查看了,所以需要清空棧 Y。
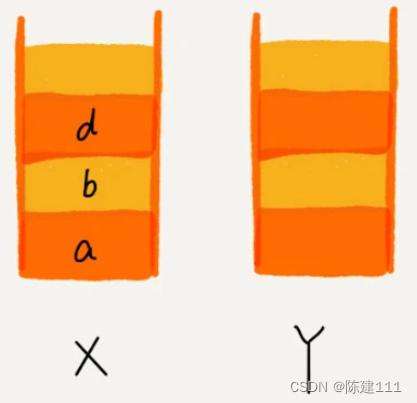
小結
棧是一種操作受限的數據結構,只支持入棧和出棧操作。后勁先出是它最大的特點。棧既可以通過數組實現,也可以通過鏈表來實現。不管基于數組還是鏈表,入棧、出棧的時間復雜度都為 O ( 1 ) O(1) O(1)。此外,還講了一種支持動態擴容的順序棧,你需要掌握其均攤時間復雜度的分析方法。







)

)

)




】)


