目錄
1.樹的概念和結構
1.1樹的概念
1.2樹的相關概念
1.3樹的代碼表示
2.二叉樹的概念及結構
2.1二叉樹的概念
2.2特殊的二叉樹
2.3二叉樹的存儲結構
2.3.1順序存儲
2.3.2鏈式存儲
3.二叉樹的順序結構和實現
3.1二叉樹的順序結構
3.2堆的概念和結構
3.3堆的特點
3.4堆的代碼實現
3.4.1堆代碼實現中的算法問題
3.4.1.1向上調整算法
3.4.1.2向下調整算法
3.4.2堆代碼 Heap.h
3.4.3堆代碼Heap.c
3.4.4堆代碼test.c
3.5堆的應用(TOP K問題)
3.5.1舉例
3.5.2解決問題代碼
4.二叉樹的鏈式結構和實現
4.1手搓鏈式二叉樹
4.2遍歷鏈式二叉樹
4.2.1前序遍歷
4.2.2中序遍歷
4.2.3后序遍歷
4.2.4層序遍歷
?編輯
4.3鏈式二叉樹的其他函數
4.3.1二叉樹節點個數,葉子節點個數,高度函數
4.3.2二叉樹第K層節點個數
4.3.3銷毀二叉樹
1.樹的概念和結構
1.1樹的概念
樹與我們之前學過的數據結構都不相同,因為其具有一個重要特征:非線性。
樹是一種非線性的數據結構,由一組節點(node)和一組連接節點的邊(edge)組成。樹的基本定義如下:
- 每個樹都有一個稱為根(root)的節點,根節點是樹的頂層節點,沒有父節點。
- 除了根節點外,每個節點可以有零個或多個子節點,子節點與父節點之間通過邊連接。
- 樹中的每個節點都有一個稱為父節點(parent)的節點,除了根節點。
- 樹中的節點可以擁有一個或多個子節點,每個子節點都有一個稱為子樹(subtree)的樹,由該子節點及其子節點構成。
- 沒有子節點的節點稱為葉節點(leaf),葉節點位于樹的底層。
- 從根節點到任意節點的路徑都唯一確定一條邊,該邊稱為該節點的父邊。
?用圖來表示就是:
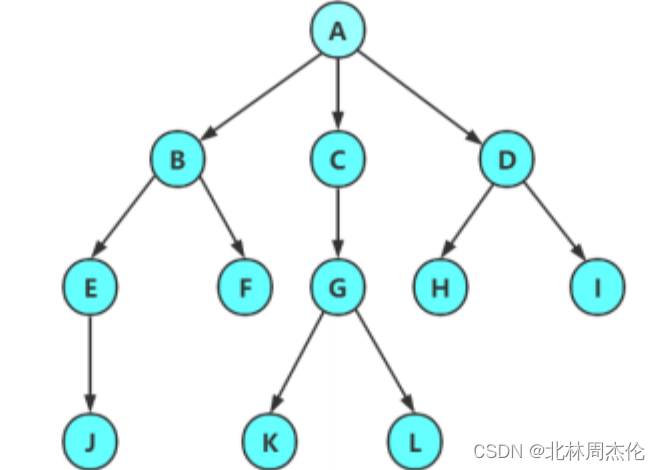
簡單來說,數據結構中樹就是一種發散性的結構,與我們之前學過的單鏈表,順序表,棧和隊列這類的線性事物完全不同。計算機中和樹有關系的就是文件夾,文件夾一般采用多層次結構( 樹狀結構 )。在這種結構中每一個磁盤有一個根文件夾 ,它包含若干文件和文件夾。
需要注意的一點是:?在樹這種結構,子樹之間不能有交集,要不然就不能構成樹了。
1.2樹的相關概念
在樹這種數據結構中包含了很多概念,這些概念基于樹的結構,利用人類親緣關系和樹木的概念名稱命名。
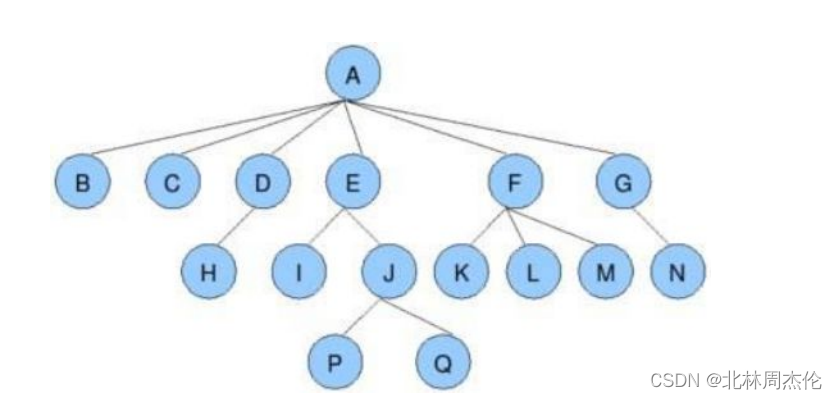
結點的度:一個結點含有的子樹的個數稱為該結點的度;如上圖:A的為6葉結點或終端結點:度為0的結點稱為葉結點;如上圖:B、C、H、I...等結點為葉結點非終端結點或分支結點:度不為0的結點;如上圖:D、E、F、G...等結點為分支結點雙親結點或父結點:若一個結點含有子結點,則這個結點稱為其子結點的父結點;如上圖:A是B的父結點孩子結點或子結點:一個結點含有的子樹的根結點稱為該結點的子結點;如上圖:B是A的孩子結點兄弟結點:具有相同父結點的結點互稱為兄弟結點;如上圖:B、C是兄弟結點樹的度:一棵樹中,最大的結點的度稱為樹的度;如上圖:樹的度為6結點的層次:從根開始定義起,根為第1層,根的子結點為第2層,以此類推;樹的高度或深度:樹中結點的最大層次;如上圖:樹的高度為4堂兄弟結點:雙親在同一層的結點互為堂兄弟;如上圖:H、I互為兄弟結點結點的祖先:從根到該結點所經分支上的所有結點;如上圖:A是所有結點的祖先子孫:以某結點為根的子樹中任一結點都稱為該結點的子孫。如上圖:所有結點都是A的子孫森林:由m(m>0)棵互不相交的樹的集合稱為森林;
1.3樹的代碼表示
樹的代碼表示和一些其他數據結構類似,都是利用指針聯系不同的數據。而樹這個數據結構特殊之處在于是由一個根數據慢慢擴展至很多其他數據。從前面的介紹我們也得知了不同數據之間大體上可以分為兩種:父子(祖先)關系和兄弟關系,聰明的發明者就是利用這一點設計出了樹的代碼表示:
typedef int DataType;
typedef struct Node
{struct Node* firstChild1; // 第一個孩子結點struct Node* pNextBrother; // 指向其下一個兄弟結點DataType data; // 結點中的數據域
}Node;注意:第一個孩子默認是父親向下最左邊的子樹。
無論父親有多少孩子節點,child指向左邊第一個孩子。

通過這個設計思路我們能從根出發找到任意一個子樹,下面是舉例:
(1)
要找到D首先利用(第一個孩子節點指針)找到B,再利用(指向下一個兄弟指針)兩次找到D。
(2)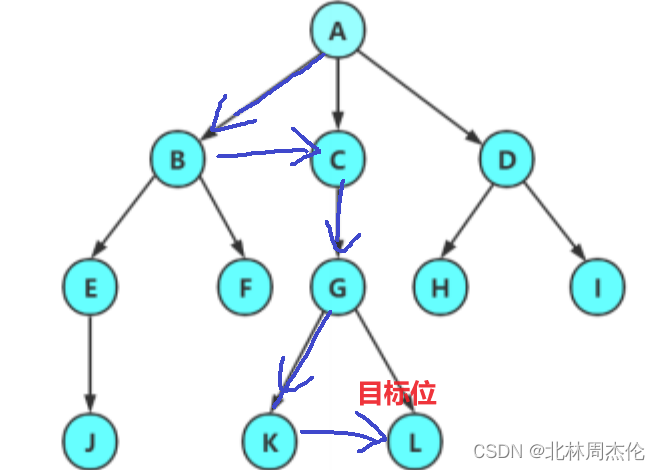
同理,找到L應該走下面這個路線。具體過程不再重復。
2.二叉樹的概念及結構
2.1二叉樹的概念
二叉樹是一種常見的樹狀數據結構,它由一組稱為節點的元素組成,每個節點最多有兩個子節點,分別稱為左子節點和右子節點。根節點是樹的頂部節點,它沒有父節點,而其他節點都有且只有一個父節點。
二叉樹是樹中比較特殊的一種,因為二叉樹中每個父節點最多只能有兩個子樹(左子樹和右子樹)。

從這張圖中我們知道:
1. 二叉樹不存在度大于2的結點2. 二叉樹的子樹有左右之分,次序不能顛倒,因此二叉樹是有序樹
2.2特殊的二叉樹
實際應用中不是所有的二叉樹我們都研究,主要有下面兩種特殊的二叉樹:

1. 滿二叉樹:一個二叉樹,如果每一個層的結點數都達到最大值,則這個二叉樹就是滿二叉樹。也就是說,如果一個二叉樹的層數為K,且結點總數是 2^k-1 ,則它就是滿二叉樹。2. 完全二叉樹:完全二叉樹是效率很高的數據結構,完全二叉樹是由滿二叉樹而引出來的。對于深度為K 的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對 應時稱之為完全二叉樹。 要注意的是 滿二叉樹是一種特殊的完全二叉樹.
2.3二叉樹的存儲結構
二叉樹的儲存結構有兩種,正好對應之前我們學過的兩種數據結構:順序表(底層是數組)和鏈表(底層是結構體和指針)。所以,二叉樹儲存分為順序存儲和鏈式存儲。
2.3.1順序存儲
順序存儲一般只適用于完全二叉樹,因為使用順序存儲要利用到數組。而使用數組存儲二叉樹就必須要用到完全二叉樹(因為這樣會滿足一定的規律,后續會詳細講),所以使用非完全二叉樹時會造成數組空間的浪費(有時需要跳過數組中的一些元素)。如下圖:
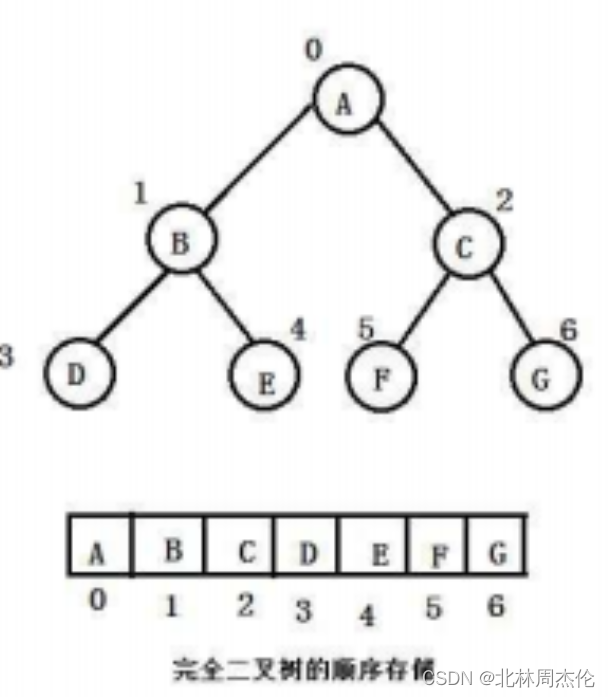
假設4位置是空的,數組中E位置就必須空出來,這樣就造成了空間的浪費。
2.3.2鏈式存儲
3.二叉樹的順序結構和實現
3.1二叉樹的順序結構
二叉樹的順序結構是指將二叉樹的節點按照順序存儲在一個數組中,同時利用數組索引來表示節點之間的父子關系。
具體而言,假設二叉樹的根節點存儲在數組索引為0的位置,任意節點在數組中的索引為i,則它的左子節點存儲在索引2i+1的位置,右子節點存儲在索引2i+2的位置。這種方式可以有效地節省空間,但在插入和刪除節點時可能需要進行數組的移動操作,因此不適用于經常需要插入和刪除操作的情況。

在用數組存儲的時候根部用0表示,每個子樹都要-1.這樣就滿足前面所說的:
左子樹=父親*2+1;右子樹=父親*2+2.

3.2堆的概念和結構
在數據結構中,堆(Heap)是一種特殊的樹形數據結構,它滿足以下兩個特性:
堆是一個完全二叉樹(Complete Binary Tree)。這意味著除了最底層之外的所有層都被完全填滿,并且最底層從左到右填充。
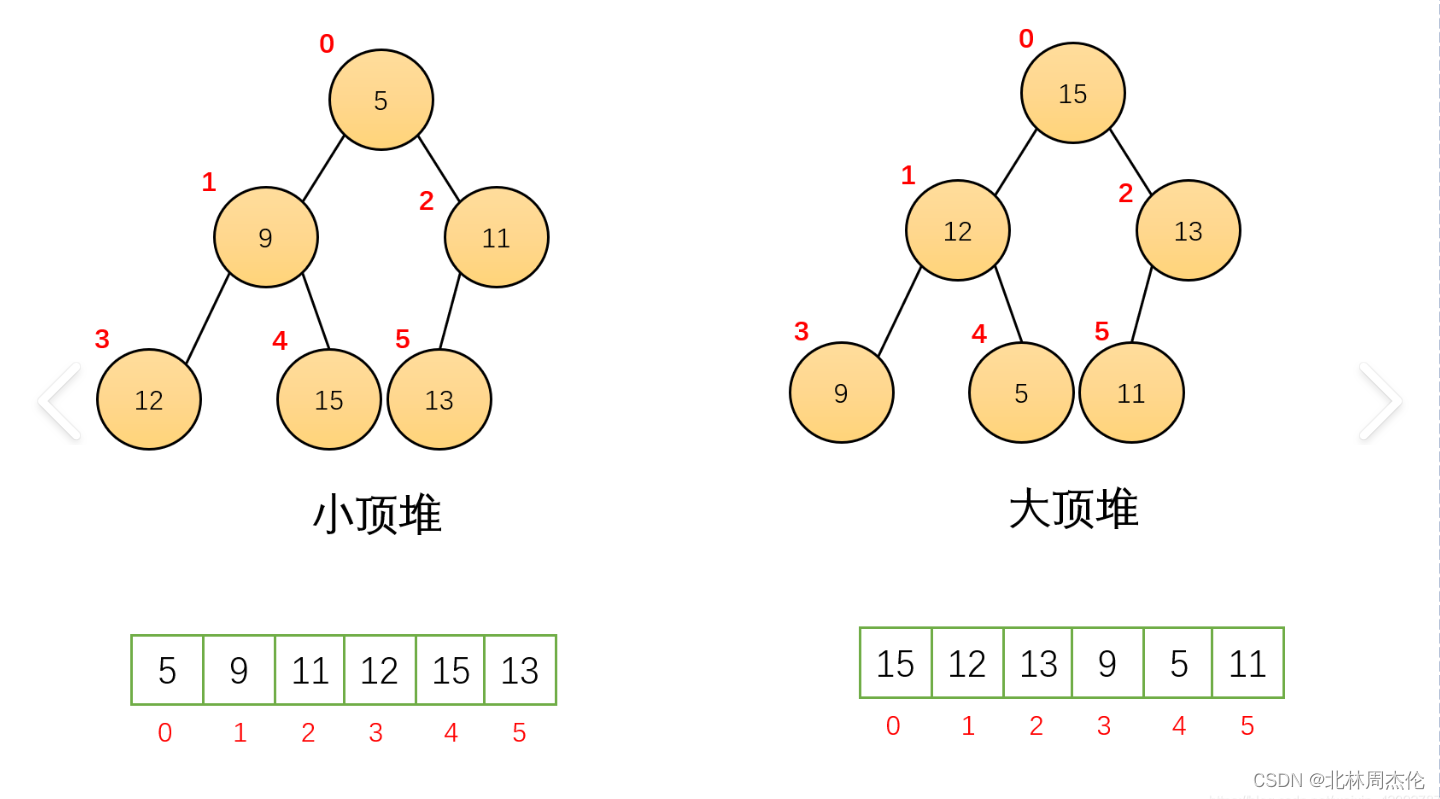
堆中的每個節點的值都必須滿足堆屬性(Heap Property):“對于大頂堆(或最大堆),父節點的值大于或等于其子節點的值;對于小頂堆(或最小堆),父節點的值小于或等于其子節點的值”。
基于上述屬性,堆可以分為兩種常見的類型:大堆和小堆。
下圖就是大堆和小堆最直觀的區別:
3.3堆的特點
無論是小堆還是大堆,祖先的位置和子樹的位置之間都有一定的關系(這一特點對后面關于對的代碼實現很有用處)。
特點如下:
1.堆是以數組作為底層的,存儲數據的邏輯結構是一顆二叉樹,存儲數據的物理結構是數組。
2.想象中的二叉樹上的每一個數據都是數組中的一個元素,都有自己的編號(就是作為數組元素的下標 )。
3.二叉樹上的數據的編號有一定的規律:
(1)由父親找兒子:左子樹=父親*2+1;右子樹=父親*2+2。
(2)由兒子找父親:父親=(兒子-1)/2.(這個公式容易記錯先-1還是先/2的話可以自己畫一個二叉樹的圖去判斷)。
3.4堆的代碼實現
3.4.1堆代碼實現中的算法問題
堆代碼中的算法問題主要解決一個有序的堆中突然插入或刪除一個數據導致有序的堆變為無序的堆的問題,我們需要涉及到的算法有向上調整算法和向下調整算法。
下面我們先來講向上調整算法:
3.4.1.1向上調整算法
這個算法主要解決的是當一個有序的堆插入新數據時怎樣重新調整至有序的狀態。
比如下面這個小堆:

它現在是一個有序的小堆存儲,如果這個時候我們插入一個新的編號為9的數據14,就像下圖:

此時它明顯不符合小堆的概念,這個時候就需要向上調整。
小堆排序中向上調整的方法與思路是:
子樹與父親進行比較,如果子樹比父親小,則與父親交換;若子樹比父親大,則不需要變動。
思路用圖來表示就是:

最后,添加了一個數據的無序堆再次變成了有序的小堆。
向上調整算法用代碼來表示就是:
//向上調整算法
void AdjustUp(DataType*a,int child)
{assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[child] <= a[parent]){int tmp = a[child];a[child] = a[parent];a[parent] = tmp;child = parent;parent = (child - 1) / 2;}else{break;}}
}3.4.1.2向下調整算法
向下調整算法比向上調整算法稍微復雜一點,用于接下來刪除堆頂數據。
還是利用我們剛剛的圖像,如果直接刪除堆頂數據就像這樣:
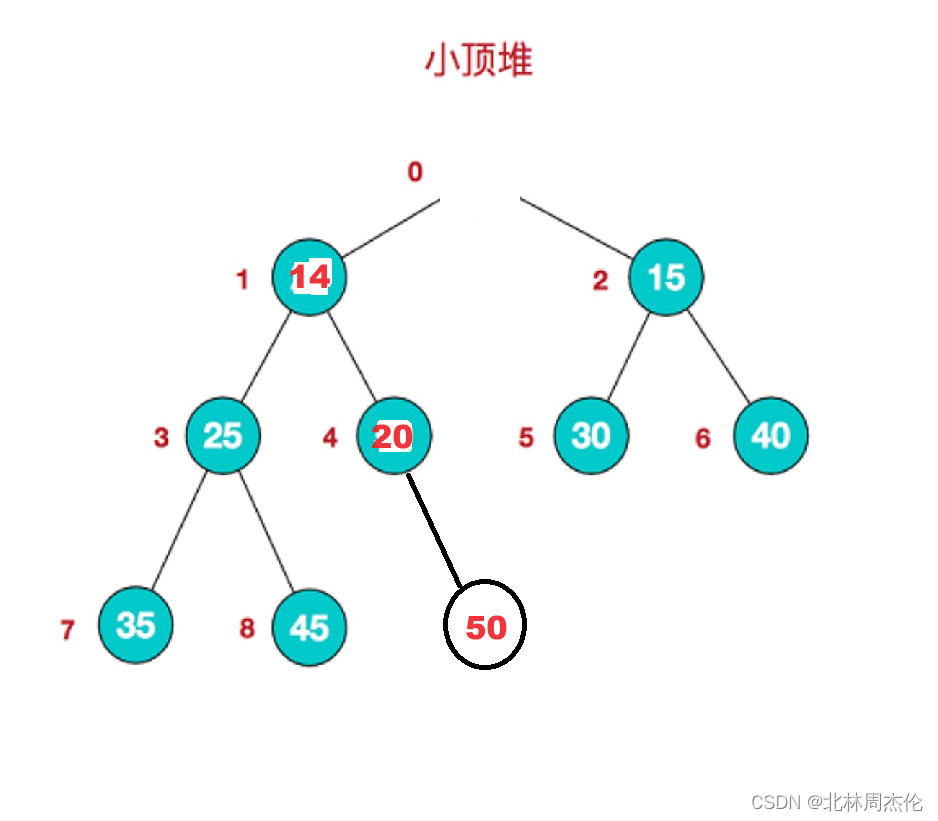
對于剩下數據的重排就比較麻煩,因為動的數據很多(不像向上調整算法一樣只要動一列從子孫到祖先的疏忽),非常麻煩。
這個時候科學家想到一種很妙的方式,思路如下:
1.先將堆頂元素和堆的最后一個元素互換。
2.刪除堆的最后一個元素(相當于刪除了先前的堆頂)。
3.利用向下調整算法將堆重新恢復至小堆。
我們先來講向下調整算法部分。
小堆排序中向下調整的方法與思路是(剛好與向上調整算法相反):
根數據與子樹進行比較,如果根數據比子樹大,則與子樹交換;若根數據比子樹大,則不需要變動。
代碼實現如下:
//向下調整算法
void AdjustDown (Heap* hp,DataType parent)
{assert(hp);//假設左孩子比右孩子要小int child = parent * 2 + 1;while (child < hp->size){// 找出小的那個孩子if (child + 1 < hp->size && hp->a[child + 1] < hp->a[child]){++child;}if (hp->a[parent] >= hp->a[child]){int tmp =hp->a[parent];hp->a[parent] = hp->a[child];hp->a[child] = tmp;parent = child;child = parent * 2 + 1;}else{break;}}
}需要注意的是:這個代碼與向上調整算法的不同之處在于使用了假設法,先假設左子樹比右子樹小,假設成功就不需要調整;若假設失敗,在使數組的下標++即可。
3.4.2堆代碼 Heap.h
堆底層還是數組,所以構成堆的結構體組成與順序表相似。
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>typedef int DataType;typedef struct Heap
{DataType* a;int size;int Capacity;
}Heap;// 堆的構建
void HeapInit(Heap* hp);
// 堆的銷毀
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, DataType x);
// 堆的刪除
void HeapPop(Heap* hp);
// 取堆頂的數據
DataType HeapTop(Heap* hp);
// 堆的數據個數
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);
//展示堆的數據
void HeapPrint(Heap* hp);//向上調整算法
void AdjustUp(Heap*hp,DataType parent);//向下調整算法
void AdjustDown(Heap* hp, DataType parent);3.4.3堆代碼Heap.c
答題的實現方式與順序表比較類似,不同的地方主要有兩個:
(1)堆數據的添加和堆數據的刪除需要引入向上調整算法和向下調整算法。
(2)堆數據的刪除需要三步:
? ? ? ? ? 1.堆頂堆底數據交換。(引入臨時變量)
? ? ? ? ? 2.刪除堆底數據。(size--即可)
? ? ? ? ? 3.向下調整算法。(調用寫好的函數即可)
#include"Heap.h"//向上調整算法
void AdjustUp(DataType*a,int child)
{assert(a);int parent = (child - 1) / 2;while (child > 0){if (a[child] <= a[parent]){int tmp = a[child];a[child] = a[parent];a[parent] = tmp;child = parent;parent = (child - 1) / 2;}else{break;}}
}//向下調整算法
void AdjustDown (Heap* hp,DataType parent)
{assert(hp);//假設左孩子比右孩子要小int child = parent * 2 + 1;while (child < hp->size){// 找出小的那個孩子if (child + 1 < hp->size && hp->a[child + 1] < hp->a[child]){++child;}if (hp->a[parent] >= hp->a[child]){int tmp =hp->a[parent];hp->a[parent] = hp->a[child];hp->a[child] = tmp;parent = child;child = parent * 2 + 1;}else{break;}}
}// 堆的構建
void HeapInit(Heap* hp)
{hp->Capacity = hp->size = 0;hp->a = NULL;
}// 堆的銷毀
void HeapDestory(Heap* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->Capacity = hp->size = 0;
}// 堆的插入
void HeapPush(Heap* hp, DataType x)
{//擴容if (hp->Capacity == hp->size){int NewCapacity = hp->Capacity == 0 ? 4 : 2 * hp->Capacity;DataType* tmp = (DataType*)realloc(hp->a,NewCapacity*sizeof(DataType));hp->Capacity = NewCapacity;hp->a = tmp;}if (hp->size == 0){hp->a[0] = x;hp->size++;}else{hp->a[hp->size] = x;hp->size++;//數據添加AdjustUp(hp->a, hp->size - 1);}
}// 堆的刪除(刪除堆頂數據)
void HeapPop(Heap* hp)
{//1.交換int tmp = hp->a[0];hp->a[0] = hp->a[hp->size - 1];hp->a[hp->size-1]=tmp;//2.刪除末尾數據hp->size--;//3.向下調整算法AdjustDown(hp,0);
}// 取堆頂的數據
DataType HeapTop(Heap* hp)
{assert(hp);return hp->a[0];
}// 堆的數據個數
int HeapSize(Heap* hp)
{return hp->size;
}// 堆的判空
bool HeapEmpty(Heap* hp)
{if (hp->size == 0){return false;}else{return true;}
}//展示堆的數據
void HeapPrint(Heap* hp)
{for (int i=0;i<hp->size;i++){printf("%d ",hp->a[i]);}
}3.4.4堆代碼test.c
#include"Heap.h"int main()
{Heap hp;// 堆的構建HeapInit(&hp);// 堆的插入HeapPush(&hp,1);HeapPush(&hp, 6);HeapPush(&hp, 48);HeapPush(&hp, 45);HeapPush(&hp, 17);HeapPush(&hp, 172);HeapPush(&hp, 51);HeapPush(&hp, 5);//展示堆的數據HeapPrint(&hp);// 堆的刪除HeapPop(&hp);printf("\n");HeapPrint(&hp);// 堆的銷毀HeapDestory(&hp);return 0;
}效果如下:

3.5堆的應用(TOP K問題)
3.5.1舉例
我們知道數據結構的學習就是為了處理數據,堆排序的一個重要應用就是可以解決TOP K問題,下面我們簡單介紹一下TOP K問題。
TOP K問題可以舉出下面的例子:
(1)(實例)假設王者榮耀有幾億個玩家,其中有一般的人都玩過亞瑟這個角色。現在系統要根據每位玩家亞瑟的數據排出全國前十的亞瑟。
(2)現在隨機生成10000個數字,要把最大的5個數字篩選出來。
我們將上述王者榮耀的例子換成整型數字,一億個數字=4億字節≈4G。現在面試官問你能否用1G的內存找出最大的10個數字?解法如下:
將1億個數字分為4堆,分4次堆排序,每次篩選出最大的10個數字,最后再對40個數字來一次堆排序,挑出最大的10個數字即可。
現在面試官改變問法:能否用1KB的內存完成上述的事情呢?方法如下:
先用前10個數字組成一個小堆,之后遍歷1億個數字,將這1億個數字都與小堆頂的數字比較。如果比小堆頂的數字大,就交換,同時再利用向下調整算法重新恢復成小堆;如果比小堆頂的數字還小就不做變動。最后留在小堆的10個數字就是最大的10個數字。這樣就可以利用最少的空間辦最大的事。
3.5.2解決問題代碼
現在我們寫出一段代碼,來證明我們的思路確實有效果。這段代碼大致意思是:給一個長度為10000的數組,生成10000個隨機數,利用代碼篩選出最大的10個數。
Heap.h , Heap.c大體上與堆代碼一致,需要修改的地方如下:
(1)新寫了一個HeapAdd函數,當遍歷數組時用這個函數來判斷數組元素是否要與堆頂元素進行交換。代碼如下:
void HeapAdd(Heap* hp, int x)
{if (x >= hp->a[0]){hp->a[0] = x;AdjustDown(hp, 0);}}(2)主函數需要改動
#include"Heap.h"int main()
{Heap hp;srand((unsigned)time(NULL));int arr[10000] = { 0 };//隨機生成10000個數字for (int i = 0; i < 10000; i++){arr[i] = rand()%10000+ i;}HeapInit(&hp);//將前10個數組成一個小堆for (int j = 0; j < 10; j++){HeapPush(&hp, arr[j]);}for (int l = 10; l < 10000; l++){HeapAdd(&hp, arr[l]);}HeapPrint(&hp);return 0;
}效果如下:

但是我們不知道找到的這10個數是不是最大的,我們要再對代碼進行小小的改動:
#include"Heap.h"int main()
{Heap hp;srand((unsigned)time(NULL));int arr[10000] = { 0 };//隨機生成10000個數字for (int i = 0; i < 10000; i++){arr[i] = rand()%10000+ i;//改動位置if (i % 999 == 0){arr[i] += 1000000;}}HeapInit(&hp);//將前10個數組成一個小堆for (int j = 0; j < 10; j++){HeapPush(&hp, arr[j]);}for (int l = 10; l < 10000; l++){HeapAdd(&hp, arr[l]);}HeapPrint(&hp);return 0;
}我們看到留了很多空白的地方就是改動位置,主要是為了創造出最大的10個數(其他的數都在20000以內,而這10個數在100000以上)。效果如下:

證明我們的代碼沒有問題,TOP K問題被成功解決。?
4.二叉樹的鏈式結構和實現
二叉樹鏈式結構的基礎結構體代碼是:
typedef struct BinaryNode
{int data;struct BinaryNode* LeftTree;struct BinaryNode* RightTree;
}BN;
每棵樹都有左右兩顆子樹,使用兩個指針分別指向他們即可。
4.1手搓鏈式二叉樹
?為了方便操作,我們手動創造一個二叉樹,后續方便寫有關二叉樹的函數。
假設我們要實現下面這個鏈式二叉樹:
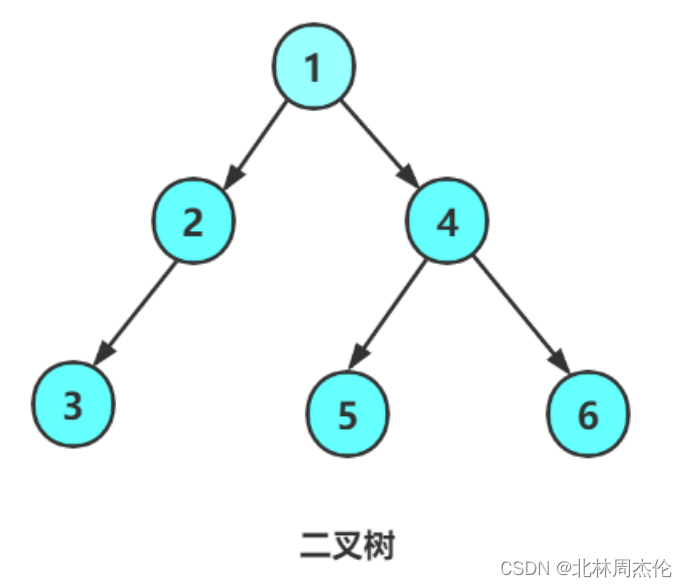
BN* BuyNode(int a)
{BN* NewCapacity = (BN*)malloc(sizeof(BN));if (NewCapacity == NULL){perror("malloc fail");}NewCapacity->data = a;NewCapacity->LeftTree = NULL;NewCapacity->RightTree = NULL;return NewCapacity;
}BN* CreatCapacity()
{BN* Node1 = BuyNode(1);BN* Node2 = BuyNode(2);BN* Node3 = BuyNode(3);BN* Node4 = BuyNode(4);BN* Node5 = BuyNode(5);BN* Node6 = BuyNode(6);Node1->LeftTree = Node2;Node1->RightTree = Node4;Node2->LeftTree = Node3;Node4->LeftTree = Node5;Node4->RightTree = Node6;return Node1;
}主函數內代碼如下:
int main()
{BN *pret=CreatCapacity();PreOrder(pret);return 0;
}4.2遍歷鏈式二叉樹
二叉樹有前序遍歷,中序遍歷,后序遍歷和層序遍歷。一般將前序,中序,后序放在一起講。下面我們就利用上面的二叉樹圖完成下面幾個遍歷。
前序,中序,后序遍歷代碼簡單且比較相似,但是理解起來有一定難度,需要用到遞歸的知識。
4.2.1前序遍歷
void PreOrder(BN* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PreOrder(root->LeftTree);PreOrder(root->RightTree);
}前序遍歷是? 根---->左邊的子樹----->右邊的子樹?這個順序來遍歷的。按照補全空子樹的順序(如下圖)應該是:1 2 3 N N N 4 5 N N 6 N N


如右圖:紅色箭頭代表的是指向節點,綠色的線代表指向節點為空時函數return?到上一層函數并且換向(從指向左子樹換成指向右子樹,即代碼中PreOrder(root->LeftTree)?和 PreOrder(root->RightTree)?的變換)。
用遞歸的思路解釋就是下面這張圖:(紅線表示跳入函數,綠線表示跳出函數)

當遇到NULL的時候函數會沿著綠線向上跳一層,當本函數的所有代碼都走完了之后,該函數也會向上跳一層(這就是為什么出現了綠線連續的情況)。
4.2.2中序遍歷
中序遍歷在代碼上的改變非常小,就是把printf和指向左子樹的PreOrder調換了一下順序。
void MiddleOrder(BN* root)
{if (root == NULL){printf("N ");return;}MiddleOrder(root->LeftTree);printf("%d ", root->data);MiddleOrder(root->RightTree);
}按照中序遍歷的思路輸出的內容應該是:N 3 N 2 N 1 N 5 N 4 N 6 N?
遞歸的思路如下圖:

4.2.3后序遍歷
后序遍歷代碼如下:
void BackOrder(BN* root)
{if (root == NULL){printf("N ");return;}BackOrder(root->LeftTree);BackOrder(root->RightTree);printf("%d ", root->data);
}按照后序遍歷的思路輸出的內容應該是:N N 3 N 2 N N 5 N N 6 4 1
遞歸的思路如下圖:

三種遍歷方式最大的不同就在于執行printf的順序不相同。
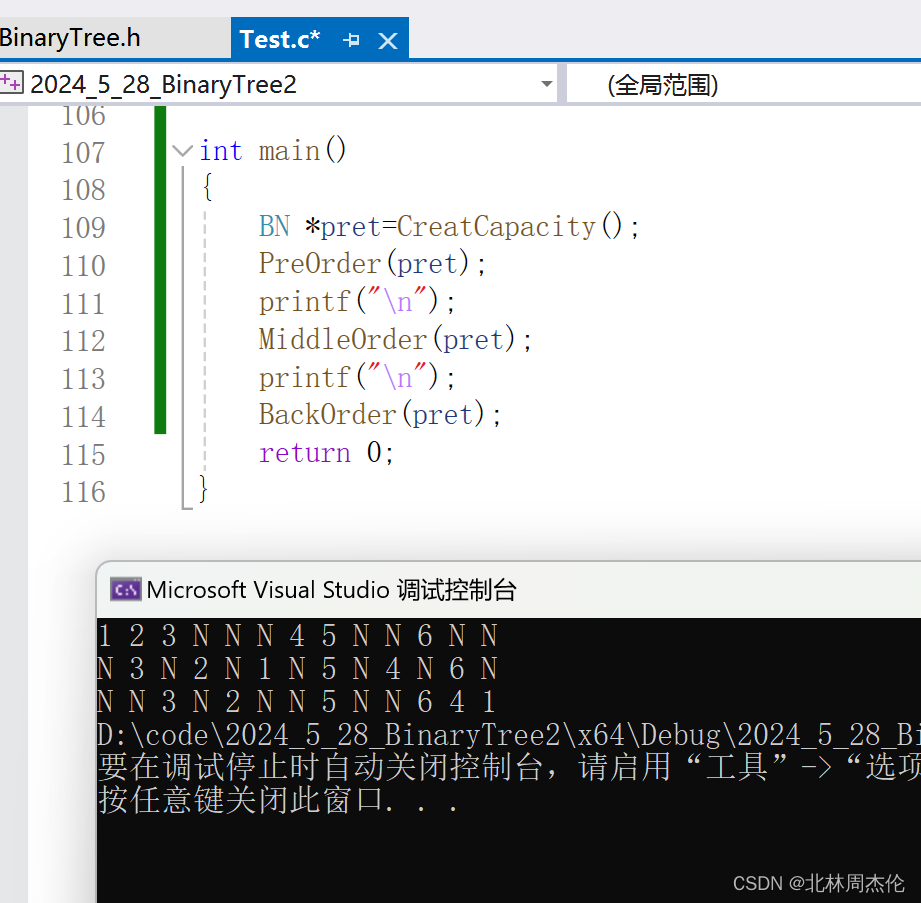
最后三種遍歷的所有代碼以及運行結果如下:
#include"BinaryTree.h"BN* BuyNode(int a)
{BN* NewCapacity = (BN*)malloc(sizeof(BN));if (NewCapacity == NULL){perror("malloc fail");}NewCapacity->data = a;NewCapacity->LeftTree = NULL;NewCapacity->RightTree = NULL;return NewCapacity;
}BN* CreatCapacity()
{BN* Node1 = BuyNode(1);BN* Node2 = BuyNode(2);BN* Node3 = BuyNode(3);BN* Node4 = BuyNode(4);BN* Node5 = BuyNode(5);BN* Node6 = BuyNode(6);Node1->LeftTree = Node2;Node1->RightTree = Node4;Node2->LeftTree = Node3;Node4->LeftTree = Node5;Node4->RightTree = Node6;return Node1;
}void PreOrder(BN* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PreOrder(root->LeftTree);PreOrder(root->RightTree);
}void MiddleOrder(BN* root)
{if (root == NULL){printf("N ");return;}MiddleOrder(root->LeftTree);printf("%d ", root->data);MiddleOrder(root->RightTree);
}void BackOrder(BN* root)
{if (root == NULL){printf("N ");return;}BackOrder(root->LeftTree);BackOrder(root->RightTree);printf("%d ", root->data);
}int TreeSize(BN* root)
{return root == NULL ? 0 :TreeSize(root->LeftTree ) + TreeSize(root->RightTree) + 1;
}int TreeLeafSize(BN* root)
{if (root = NULL){return 0;}if (root->LeftTree == NULL && root->RightTree == NULL){return 1;}return TreeLeafSize(root->LeftTree) + TreeLeafSize(root->RightTree);}int TreeHeight()
{}int main()
{BN *pret=CreatCapacity();PreOrder(pret);printf("\n");MiddleOrder(pret);printf("\n");BackOrder(pret);return 0;
}
4.2.4層序遍歷
層序遍歷顧名思義就是一層一層地讀取數據遍歷二叉樹。其概念如下:
層序遍歷是二叉樹遍歷的一種方法,也稱為廣度優先遍歷。它按照樹的層級順序逐層遍歷樹的節點。具體操作是從根節點開始,先將根節點加入隊列,然后依次取出隊列中的節點,訪問該節點,并將其左右子節點加入隊列。重復該過程,直到隊列為空為止。這樣可以保證按照從上到下,從左到右的順序遍歷整個二叉樹。
像下面這種遍歷順序:

這種遍歷方式不能再用遞歸的方式寫出,聰明的科學家想到了用隊列實現層序遍歷。具體的操作流程如下:
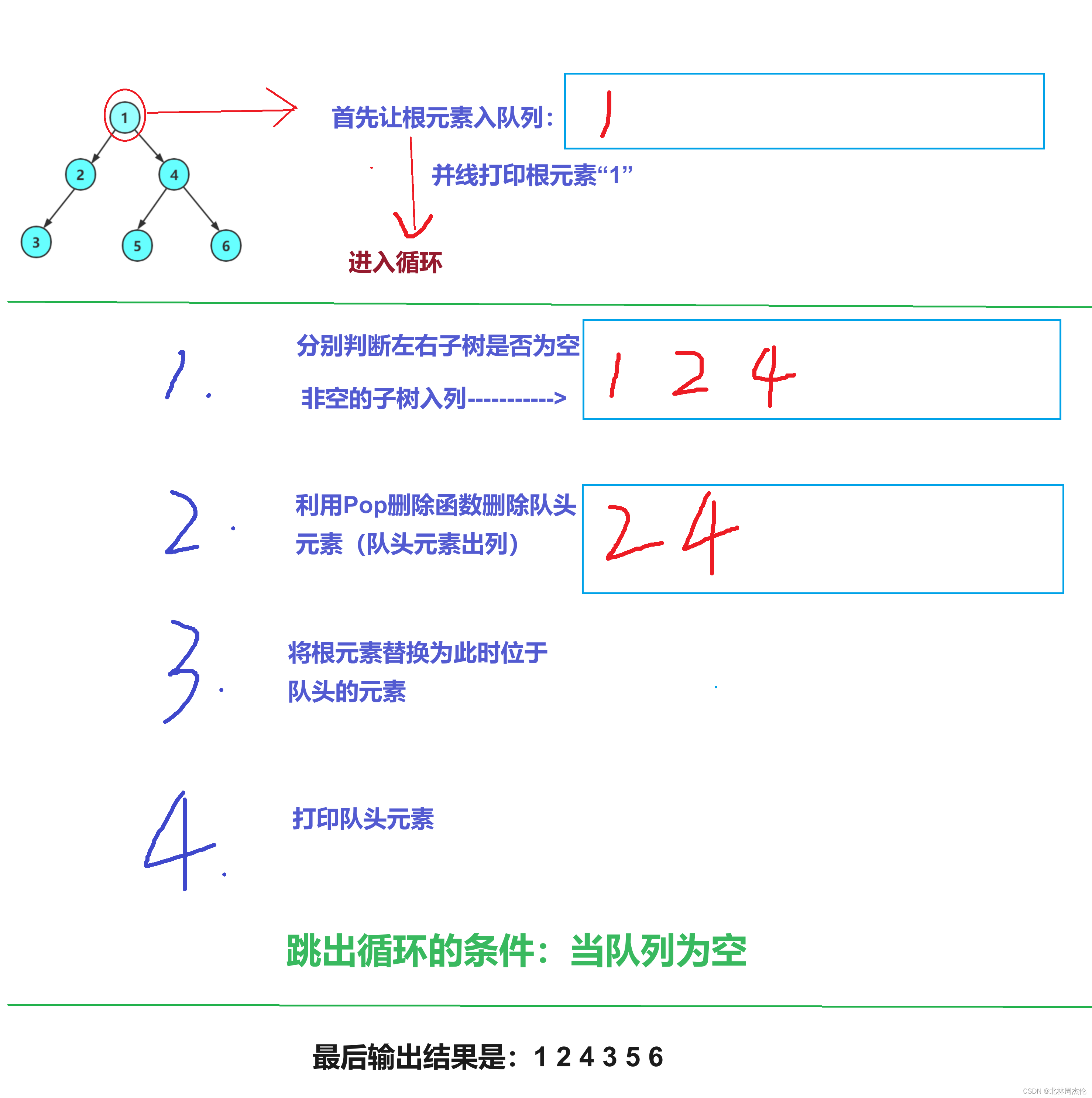
圖上展示的只是一次循環,完整循環我們來用文字表示:
第1步: 1? ? ? ? ? (打印1)
第2步: 1 2 4? ? (1的左右子樹入列)
第3步: 2 4? ? ? ?(打印并刪除1)
第4步: 2 4?3? ? (2的非空子樹入列)
第5步: 4 3? ? ? ?(打印并刪除2)
第6步: 4 3 5 6 (4的左右子樹入列)
第7步: 3 5 6? ? (打印并刪除4)
第8步: 5 6? ? ? ?(打印并刪除3)
第9步:6? ? ? ? ? ?(打印并刪除5)
第10步:NULL? (打印并刪除6)
代碼實現如下:
void LayerOrder(BN* root,Queue*q)
{QueueInit(q);if (root == 0){return ;}else{QueuePush(q,root);printf("%d ", root->data);}while (q->size){if (root->LeftTree != NULL){QueuePush(q, root->LeftTree);}if (root->RightTree!= NULL){QueuePush(q, root->RightTree);}QueuePop(q);if (q->Fir != NULL){root = q->Fir->root;}else{break;}printf("%d ", QueueFront(q));}printf("\n");}?入列函數與我們之前寫的函數有一些改動,一個參數改成了指針,修改之后的入列函數如下:
// 隊尾入隊列
void QueuePush(Queue* q, BN*Node)
{assert(q);QNode* Newnode = (QNode*)malloc(sizeof(QNode));Newnode->val = Node->data;Newnode->root = Node;//判斷隊列是否有元素if (q->Las == NULL){q->Fir = q->Las = Newnode;}else{q->Las->next = Newnode;q->Las = Newnode;//和下面的代碼一個意思/*q->Las->next = Newnode;q->Las =q->Las->next;*/}q->size++;
}我們來對層序遍歷進行檢驗:

現在再添加一個數據“7”(加在3的右子樹上):
BN* CreatCapacity()
{BN* Node1 = BuyNode(1);BN* Node2 = BuyNode(2);BN* Node3 = BuyNode(3);BN* Node4 = BuyNode(4);BN* Node5 = BuyNode(5);BN* Node6 = BuyNode(6);BN* Node7 = BuyNode(7);Node1->LeftTree = Node2;Node1->RightTree = Node4;Node2->LeftTree = Node3;Node4->LeftTree = Node5;Node4->RightTree = Node6;Node3->RightTree = Node7;return Node1;
}結果如下:
4.3鏈式二叉樹的其他函數
4.3.1二叉樹節點個數,葉子節點個數,高度函數
除了遍歷,鏈式二叉樹還有其他函數。
二叉樹節點個數,二叉樹葉子節點個數,二叉樹高度函數
代碼如下:
int TreeSize(BN* root)
{return root == NULL ? 0 :TreeSize(root->LeftTree ) + TreeSize(root->RightTree) + 1;
}int TreeLeafSize(BN* root)
{if (root == NULL){return 0;}if (root->LeftTree == NULL && root->RightTree == NULL){return 1;}return TreeLeafSize(root->LeftTree) + TreeLeafSize(root->RightTree);}int count = 1; int max = 0;
int TreeHeight(BN*root)
{if (root == NULL){return 0;}if (root->LeftTree == NULL && root->RightTree == NULL){if (max <= count){max = count;}return 1;}count++;TreeHeight(root->LeftTree);TreeHeight(root->RightTree);return 1;}
這3個函數主要用的就是遞歸的方法,在判斷條件和返回值上注意一下就能分析出來。
1.二叉樹節點個數函數:當節點不為空時就重復調用函數(先是根節點的左子樹再是右子樹)并且每次+1,相當于把二叉樹遍歷一遍。
2.二叉樹葉子節點函數。葉子就是外層兩個子樹都為空的節點。當根就是空的時候,直接返回0,根的左右子樹均為0的時候代表已經到葉子處了,于是返回1.再運用遞歸的手法不斷深入遍歷二叉樹直至找到所有葉子為止,并返回葉子的個數。
3.二叉樹高度函數。二叉樹的高度就是最深的節點的深度。要創建兩個全局變量來記錄每次最深節點的深度,最后篩選出最大的那個。深入方式就是每調用一次函數count++,當走到葉子時(到底的時候),就做判斷,如果count比max大就賦值給max,最后就能取得最大值了。
測試效果如下:

再改動一下數據,將數據7掛在6的右子樹,將8掛在7的左子樹,測試結果如下:

4.3.2二叉樹第K層節點個數
代碼如下:
int TreeLevelKSize(BN* root, int k)
{assert(k > 0); //斷言從根節點算起不存在第0層的節點if (root == NULL)return 0;if (k == 1)return 1;return TreeLevelKSize(root->LeftTree, k - 1)+ TreeLevelKSize(root->RightTree, k - 1);//從根節點開始,分別向左子樹和右子樹深入k-1層;//當二叉樹的最深處都比所要查找的層數大則使用assert報錯。
}4.3.3銷毀二叉樹
代碼如下:?
// 二叉樹銷毀
void BinaryTreeDestory(BN* root)
{if (root == NULL)return;BinaryTreeDestory(root->LeftTree);BinaryTreeDestory(root->RightTree);free(root);
}結語:二叉樹一些基本內容幾乎都在本篇文章中,謝謝閱讀,如有錯誤請批評指正?




)









)





