題目

n(3<=n<=100)個點的有向圖，

圖的邊的關系未知，但保證以下兩點：

1. 只存在j->i（i<j）的邊

2. 對于任意三個點i、j、k（i<j<k），要么k可以到達i，要么k可以到達j，要么j可以到達i

每次你可以詢問兩個點，? i j（i<j），如果j可以到達i，返回YES，否則返回NO

你需要將圖染成黑白兩色，

使得黑色的任意兩個點x、y（x<y），都滿足y可到達x，

且白色的任意兩個點x、y（x<y），都滿足y可到達x

你有最多2n次詢問機會，可以證明答案一定存在

最終輸出n個點染色的情況，輸出0表示染黑色，為1表示染白色

圖不是交互式的，也就是說圖一開始是固定下來的，不會隨詢問的改變而動態變更

實際t(t<=100)組樣例，但保證sumn不超過1000

思路來源

亂搞ac

題解

其實也不完全是算亂搞，一開始wa了，后來看了下數據的反例修了下就過了

首先原圖肯定可以拆分成兩條鏈，這樣對于三個點，一定存在兩點共鏈，就滿足題意了

然后考慮這個圖的形狀可能是怎樣的，一開始是想的雙螺旋結構的

維護兩條鏈，開始只有點n，然后點n-1如果在點n下游就接上去，否則就新開一條鏈，

然后這兩條鏈可以匯集在一點，后續在這點之后繼續擴，類似Y型，

然后Y型后續還能拆成兩個分支，再成兩條鏈，后續兩條鏈再能合并成一個點，重復若干次

然后輸出的話，就沿著點n，往下找一個下游，直接找齊一條鏈，這樣另一條鏈就自然另一種顏色

但是，遇到了一個反例

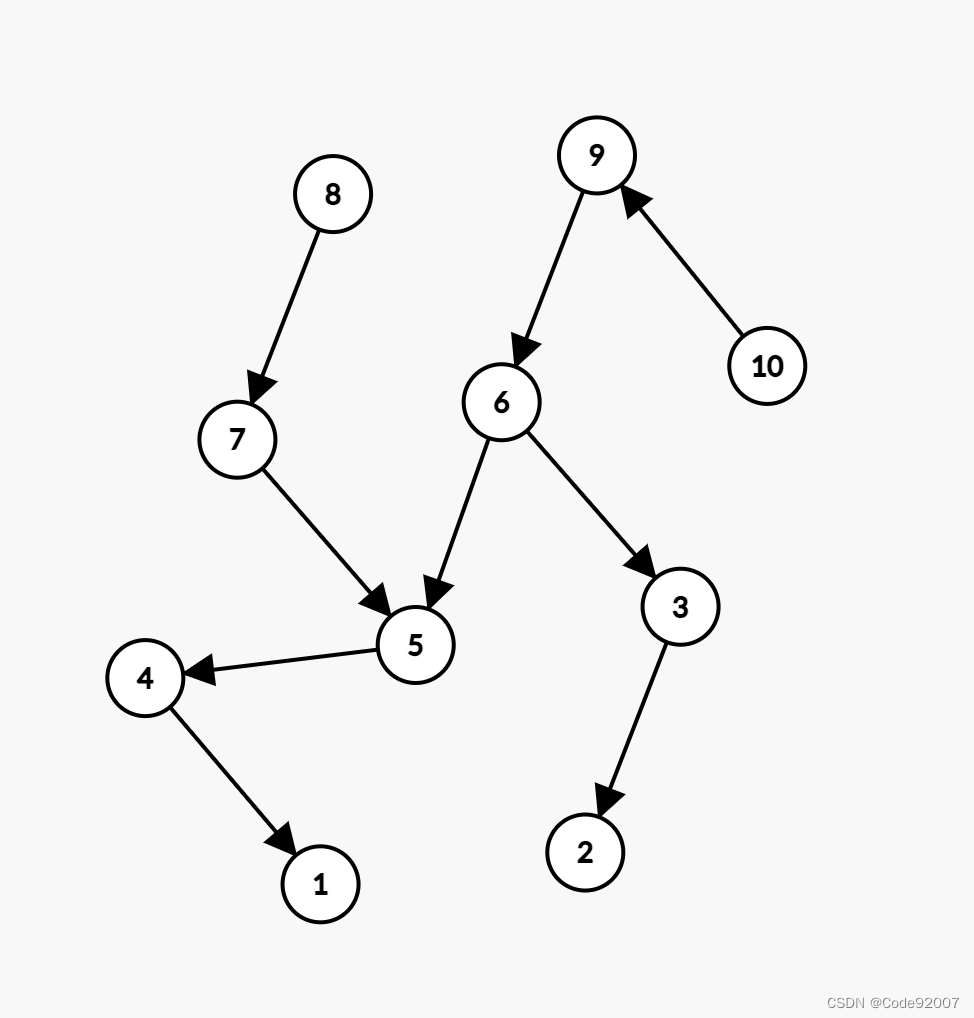
可以發現，在點5形成Y字型，后接點4之后，新來的點3并沒有續到點4上，

也沒有續到點5上，而是續到了點6上，

此時我找的鏈是10->9->6->5->4->1，就使得另一條鏈8->7和3->2不連通

而此時應該是10->9->6->3->2，另一條鏈8->7->5->4->1

這表明，當出現Y形狀的交點時（也就是圖中的5點）后，代表兩條鏈合成了一條鏈（合并）

這時候這條鏈往下接了點4，

新來的點3，可以接在點4后，也可以接在點5后，也可以接在點6后，也可以接在點7后，

這四種情況，都能使原圖被劃分成兩條鏈，

對于5->4鏈上有多個點的情況，不妨只視為有Y字形交點（點5）、Y字形尾部點（點4）兩個點

因為在鏈中間的點后面續新的點，都可以看成是在交點后面續新的點，不影響兩條鏈的性質

此外注意到，點3的出現，使得一條鏈又變成了兩條鏈（拆分）

這兩條鏈后續仍然可能再形成新的Y字形，也就是分分合合的過程可能出現若干次

所以，做法是：

1. 初始時，點n當第一條鏈的鏈尾

2. 當前如果有兩條鏈，記他們的鏈尾分別為f和s，當前要續的點是i，

（1）i如果能同時往f和s后面續，代表兩條鏈合成了一條

（2）否則，如果能往第一條鏈后面續，就往第一條后面續

（3）否則，如果能往第二條鏈后面續，就往第二條后面續

（4）否則，兩條鏈都續不了，記兩條鏈上一次合并成Y字形交點（也就是上圖的點5）為las，如果能往las后面續，就往las后面續

（5）否則，記las的兩個父親為f1、f2（也就是上圖的點6、點7），如果能往f1后面續，就往f1后面續

（6）否則往f2后面續

3. 如果當前只有一條鏈，能續則續，不能續的時候，新開一條鏈即可

代碼里加了如果不存在則為-1的情況，以及加了詢問的記憶化，統一了部分情況的分類討論

詢問次數想了一下，是不超過2n的，因為最極端的情況是上圖點3不能續到點4后面的情況

此時有4種情況，需要最多詢問3次才能確認是哪種情況，

而這種情況的出現，說明前面有一個只詢問了1次的點，也就是在點5下面的點4，

這兩個點均攤一下，平均次數就不超過2了

代碼

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
const int N=105;
int t,n,col[N];
vector<int>e[N];
int mp[N][N];
char s[10];
void clr(int x){if(x<0)return;e[x].clear();
}
void add(int x,int y){if(x<0)return;e[x].pb(y);
}
bool ask(int i,int j){if(i>j)return 0;if(~mp[i][j])return mp[i][j];printf("? %d %d\n",i,j);fflush(stdout);scanf("%s",s);return mp[i][j]=(strcmp(s,"YES")==0);
}
void out(){printf("! ");rep(i,1,n){printf("%d%c",col[i]," \n"[i==n]);}fflush(stdout);
}
int main(){sci(t);while(t--){memset(col,0,sizeof col);memset(mp,-1,sizeof mp);sci(n);rep(i,1,n)e[i].clear();int f=n,s=-1,las=-1,f1=-1,f2=-1;bool x,y;per(i,n-1,1){x=ask(i,f),y=ask(i,s);if(x && y){add(f,i);add(s,i);las=i,f1=f,f2=s;f=i,s=-1;}else if(x){add(f,i);f=i;}else if(y){add(s,i);s=i;}else{if(las==-1)s=i;else{y=ask(i,las);if(y){add(las,i);s=i;continue;}y=ask(i,f1);if(y){clr(f1);add(f1,i);s=i;}else{clr(f2);add(f2,i);s=i;}}}}for(int i=n;;i=e[i][0]){col[i]=1;if(e[i].empty())break;}out();}return 0;
}