算法簡介：
K-近鄰法（KNN）是一種簡單而有效的分類算法，也可用于回歸問題。它的基本原理是根據待分類樣本與訓練樣本的距離，選取最近的K個樣本進行投票決定分類。該算法無需訓練過程，而是利用訓練數據集直接進行預測。KNN算法簡單易懂，對于非線性問題有很好的適應性，但對于大型數據集計算量較大。在MATLAB中，可以使用fitcknn函數來訓練KNN分類模型，使用predict函數對新樣本進行預測。
部分代碼：
x=randn(1,2);%待判樣本
hold on,plot(x(1),x(2),'m+','MarkerSize',10,'LineWidth',2)
for i=1:2*Ndist(i)=norm(x-X(i,:));
end
[Sdist,index]=sort(dist,'ascend');
K=5; %近鄰數目
for i=1:Khold on,plot(X(index(i),1),X(index(i),2),'ko');
end
legend('Cluster 1','Cluster 2','x','Location','NW')
flag1=0;flag2=0;
for i=1:Kif ceil(index(i)/N)==1flag1=flag1+1;elseif ceil(index(i)/N)==2flag2=flag2+1;end
end
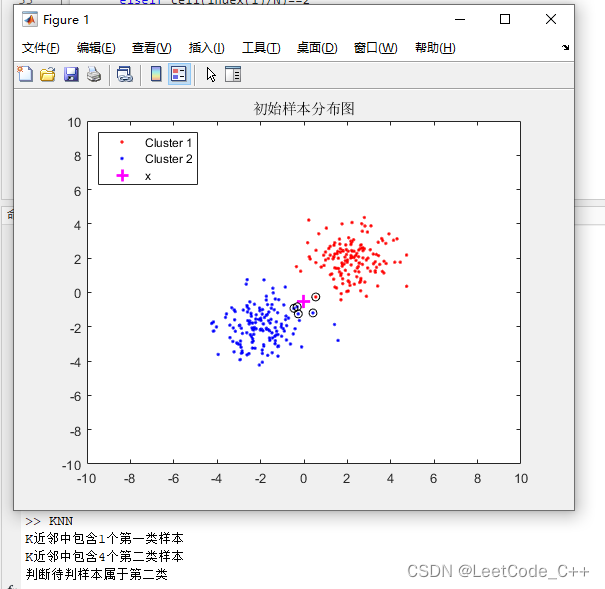
disp(strcat('K近鄰中包含',num2str(flag1),'個第一類樣本'));
disp(strcat('K近鄰中包含',num2str(flag2),'個第二類樣本'));
if flag1>flag2disp('判斷待判樣本屬于第一類');
elsedisp('判斷待判樣本屬于第二類');
end結果展示：
