前言

接上節：simulink-仿真以及PID參數整定

系統模型的辨識工作，在控制領域，一般用于開發控制器的先手工作。一般而言，設計控制器，會依據被控對象的數學模型。依據其數學模型，可以分析其各種特性，所以數學模型就顯得很重要。

數學模型，通俗一點講就是一個數學表達式，f(x, t)，這個表達式有個特點就是，給（輸入）x 賦值，那么這個表達式就會是一個關于時間 t 的函數，就會在時間軸上，隨著時間變化而變化，呈現出的輸出值，就會和實際的物理模型的輸出近似。

為什么說是近似呢，實際生活中，物理模型的實際輸出大多都會相對復雜，并不是有特別明顯的規律，有的可能會隨時間、環境以及各種情況變化而變化，那么還用一個固定的公式表示其輸出，就不準確了。也有一些簡單的物理模型，這樣的模型就很容易，就直接可以用簡單的數學公式表示其輸出。

那么可能會有新手和我一樣疑惑，既然有的不準確，那就用一些高級的方法去擬合得到實際物理對象的數學模型。有沒有方法，也有，但是考慮到情況的復雜度，用統計學的方法去擬合，也不能覆蓋全部的情況下的數學模型，所以隨后的數學模型也只能做到近似。

那么問題又來了，既然是近似，橫豎結果不能完全一致，那何必用那么復雜的方法去得到數學模型呢。所以就是這個想法，就有了高階模型線性化處理，或者降階數，能夠用最簡單的一階模型去表示物理對象的輸出，就不用二階模型，就秉承這個原則，去簡化數學模型。

那么什么情況下用一階什么時候用二階呢，有這么一段話，但是很繞口，簡單說就是要給物理對象一個輸入信號，可以是階躍信號，看從一個值變化到另一個值，物理對象的實際輸出結果的變化曲線，由變化曲線來判斷。

這里說的是對一個系統不知道的情況下，采取的辦法，這個辦法又被通俗的叫作工程試驗法，給一個激勵信號，看輸出動態響應，然后有輸入和輸出結果，就可以借助工具箱里的系統辨識去擬合系統的數學模型。

在開始說系統辨識的方法前，還要解釋一下前邊的兩個問題：

1. 既然最后得到的數學模型只是近似模型，那么設計的控制器能有用么？這個問題就是控制器需要解決的問題，最經典的PID控制器，就是包含了這點，它允許模型不準確。所以大多的控制器都具備一定的容錯能力，本身控制器的作用就是降低誤差，只要這個誤差不是太大，就能救回來。那些嚴格綁定被控對象數學模型的控制器，就更加適用在準確的數學模型上。
2. 準確的數學模型又從哪里來呢？最常見的運動的質點，物理中學過的 s = v0 x t + 1/2 x a x t^2 ， 這個質點可以稍微放大一下，就變成遙控小車。那么遙控小車的運動學模型就是這個公式，輸入加速度后，路程就和時間相關，隨時間變化。但是實際小車沒這么簡單，小車還有質量，小車也不是手推的，需要提供電，由電機轉動驅動小車，那么就涉及驅動力多大，能提供多大加速度，小車需要變速，那么要平滑變速，就需要加速度控制，那么就要有動力學公式，一個運動學，一個動力學，兩個公式就是小車的數學模型，在不考慮什么復雜環境下，風阻，地面摩擦力降低這些情況，數學模型就是精準的，所以科研分析大多是先有推導的公式，然后才會有一些沒法計算推導得到的系統進行掃頻然后系統辨識 。

系統辨識

上邊說了，辨識模型就需要激勵信號輸入，和響應信號輸入，由輸入、輸出才能辨識。

常用的激勵信號，是一個組合信號，階躍、正弦、斜坡、啁啾信號：

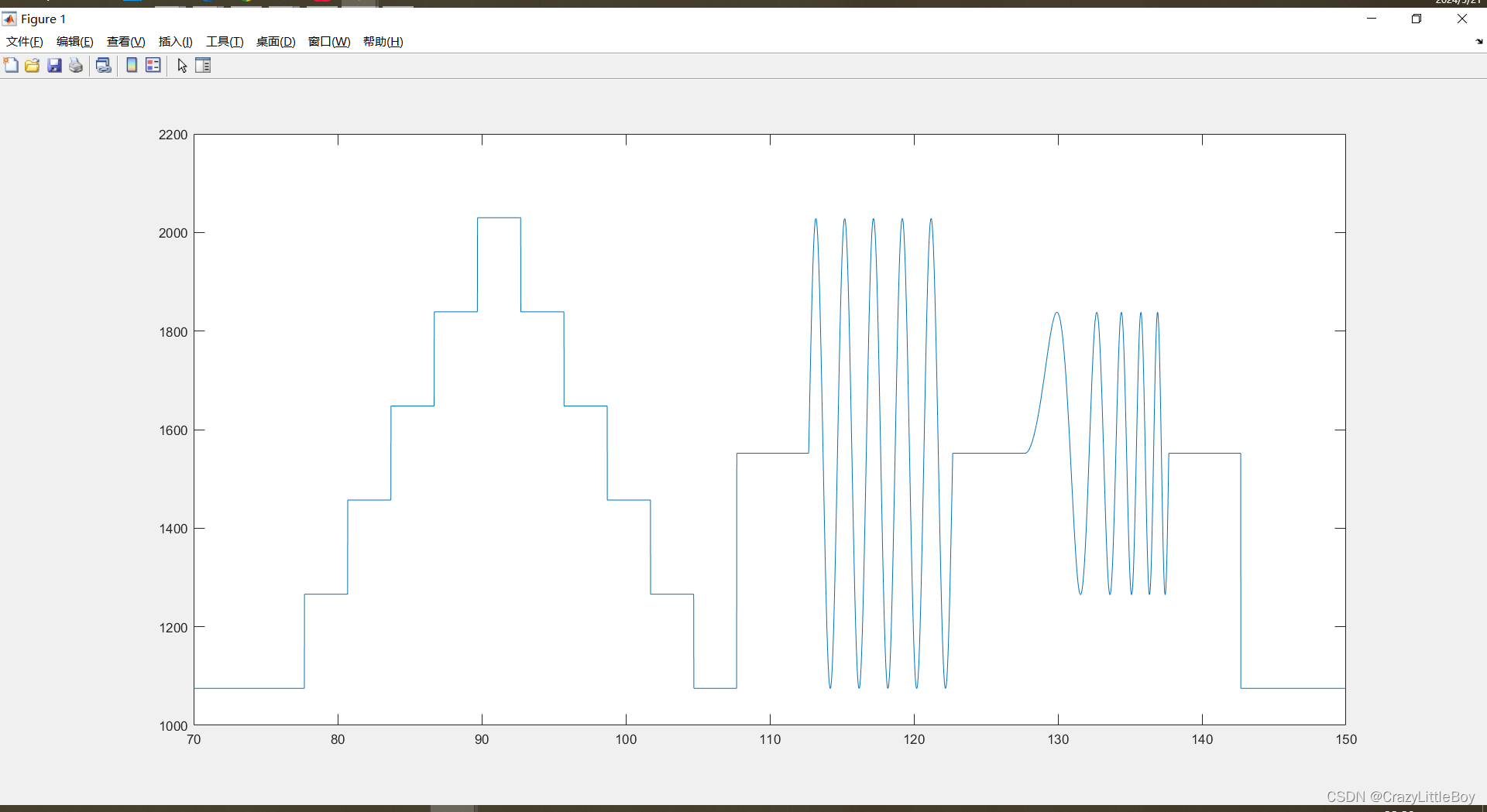
然后會得到一個對應的輸出：

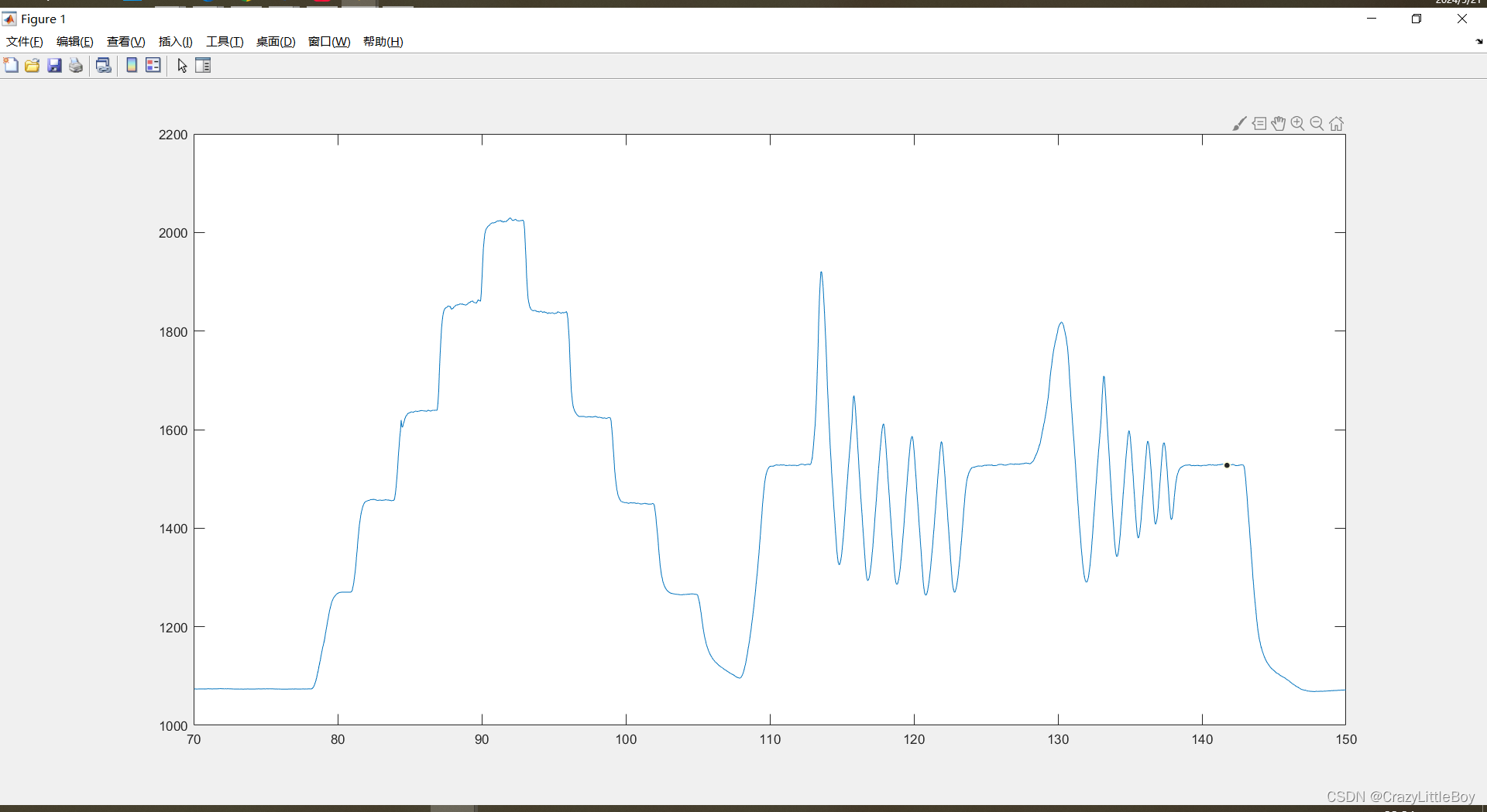
這個輸出肯定不是一個實際的物理對象的輸出，一般情況下，實際輸出和輸入不在一個維度上，比如上邊的小車模型，實際輸出是路程，輸入是加速度，在做控制器的時候，路程和加速度沒法做加減，為什么作加減，閉環控制嘛，就得把輸出送回來和輸入目標值進行對比嘛，那么就得在同一個維度下進行了。為了方便辨識，我們把輸出轉換成輸入相同的維度，這樣就可以直接使用，最后得到的系統輸出的值，就是轉換后，這個在最后不要忘記了。

圖片是為了展示效果，實際上要把數據導入matlab整理好成這樣：

第一步 選取時域數據到app

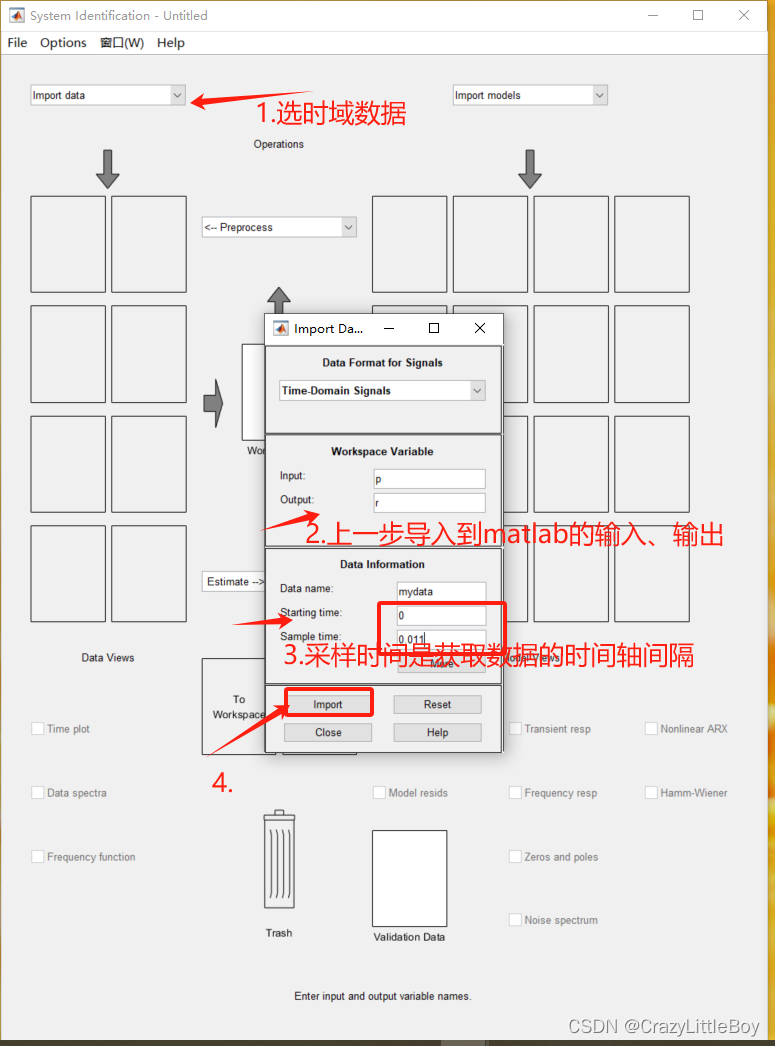
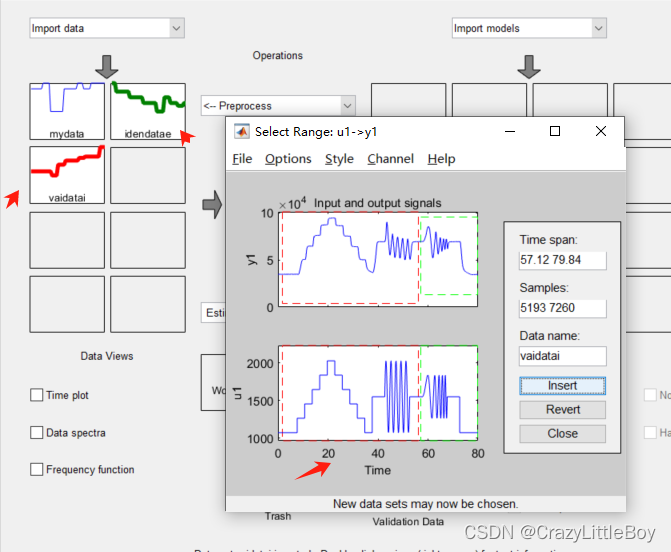
第二步 分割數據

這一步將數據分割成測試集和驗證集

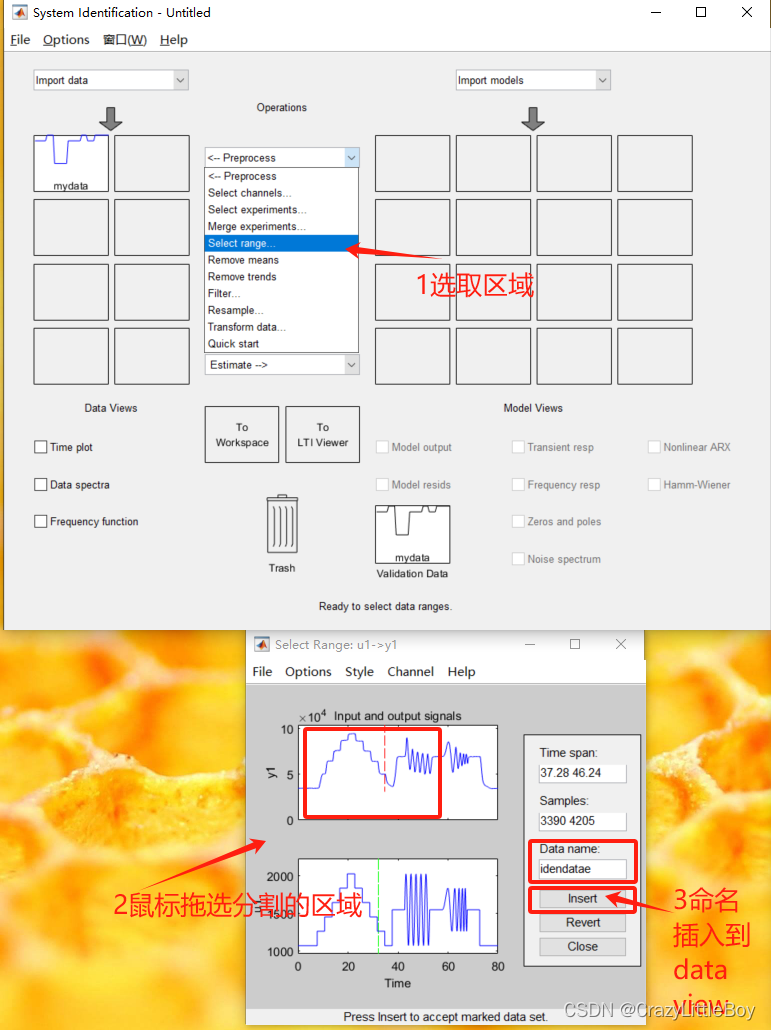
然后就會得到這個狀態：

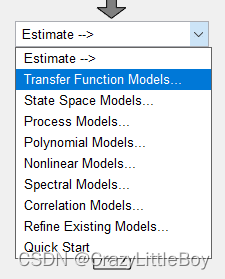
第三步 設置傳遞函數的參數

最保守的就是第一個，或者 process models 比較直觀,或者就是最后一個什么都不用設置

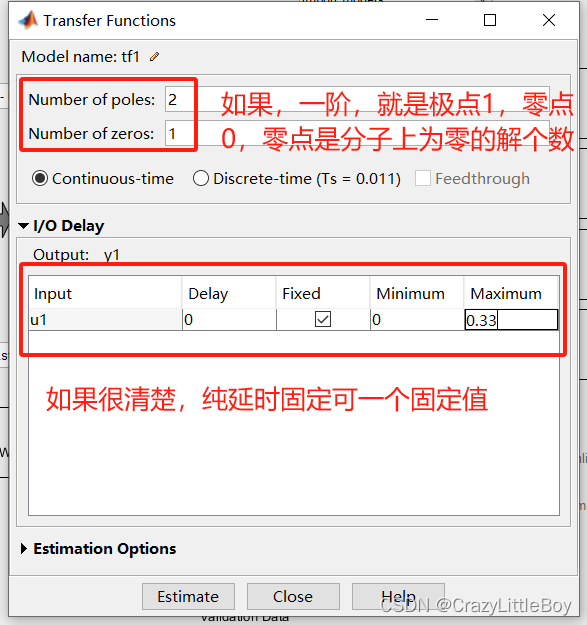
第四步 Estimate

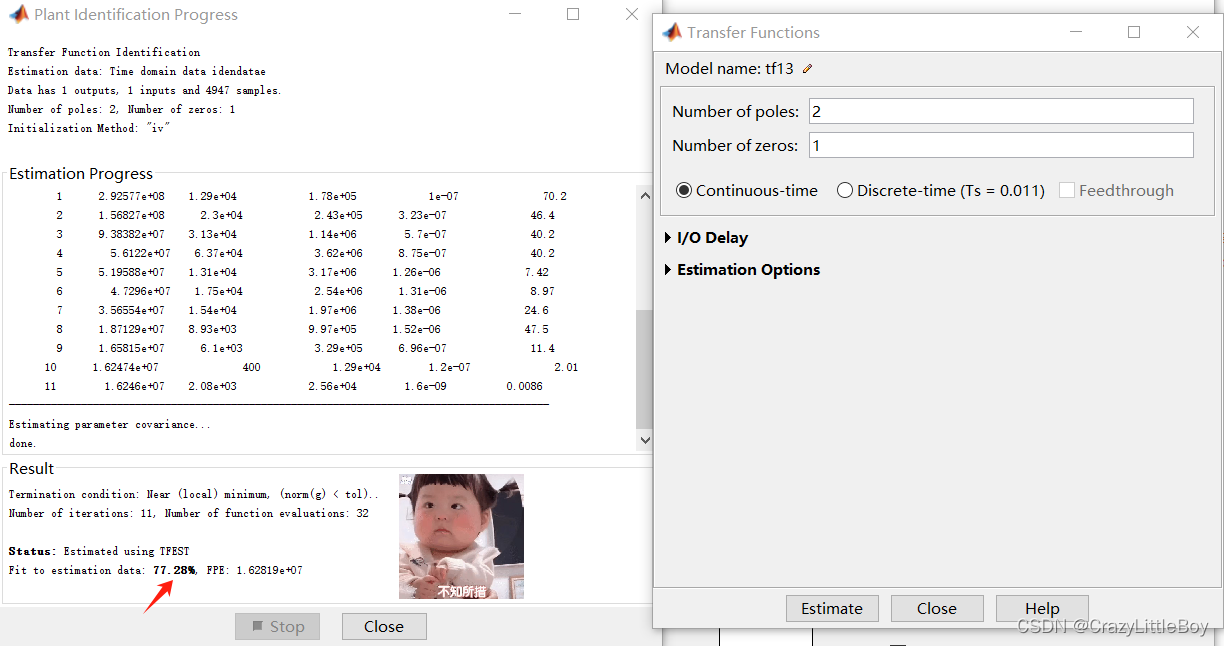
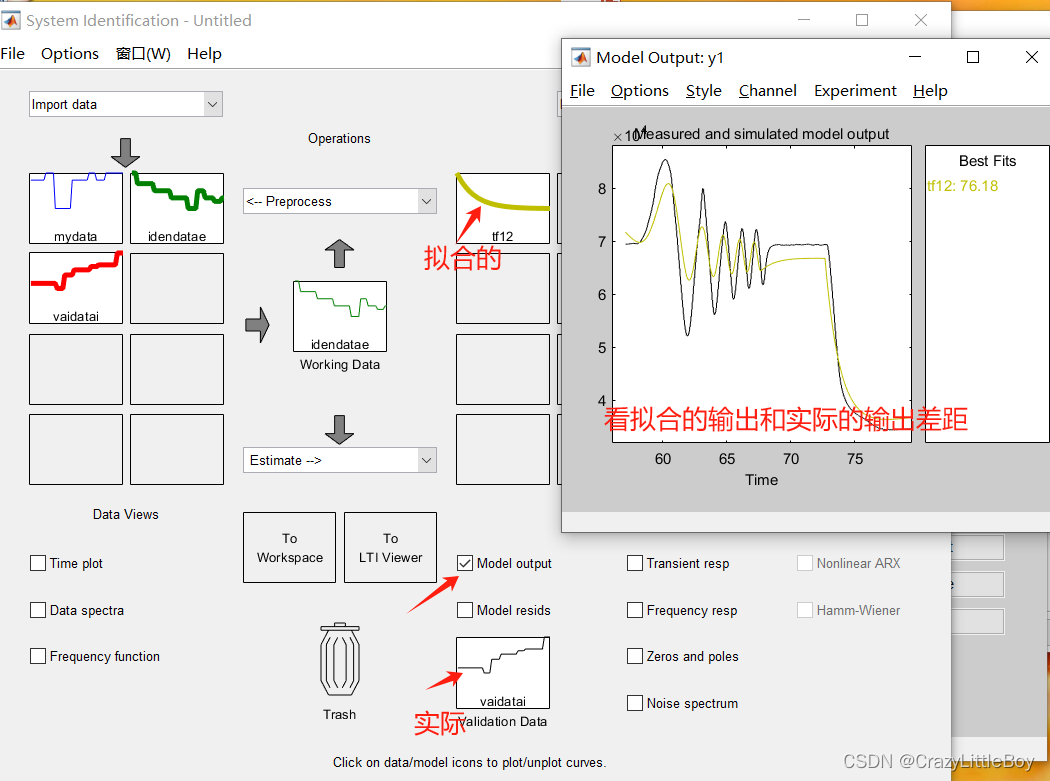
第五步

在選擇階數前可以先用state space model 推薦最合適的階數

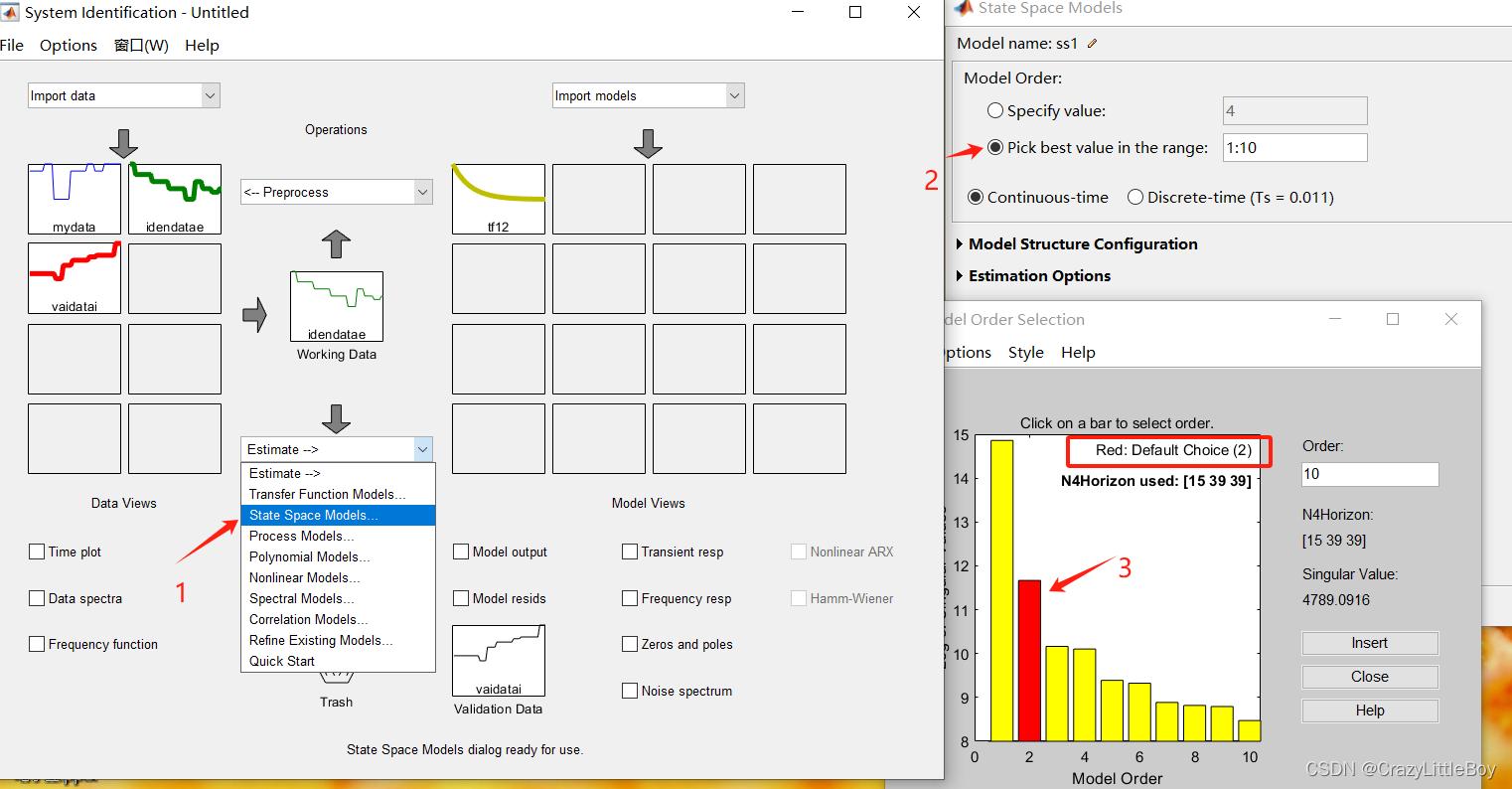
然后就來回試一試，找到擬合度最好的一個模型，那個就是辨識得到的模型：

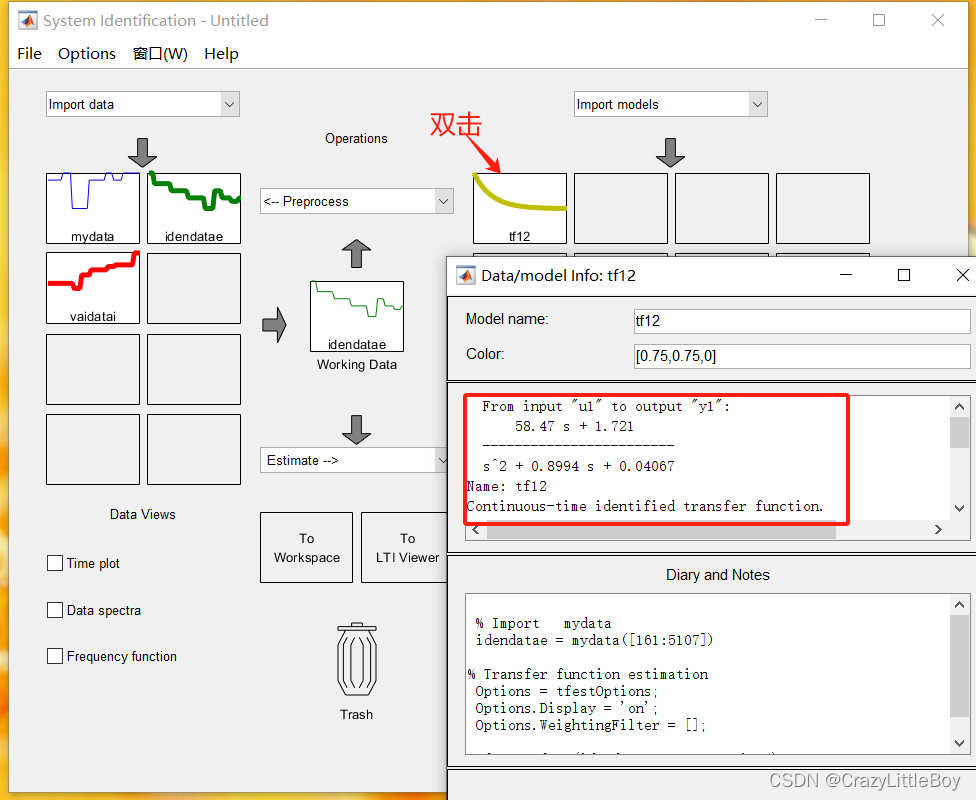
結束

打完收工，其實得到的模型只是一個輔助，應為采集到的數據到擬合，有很多需要注意的地方，最后得到的模型不一定理想。