leetCode. 85. 最大矩形

---

部分參考上一題鏈接
leetCode.84. 柱狀圖中最大的矩形

---

此題思路

---

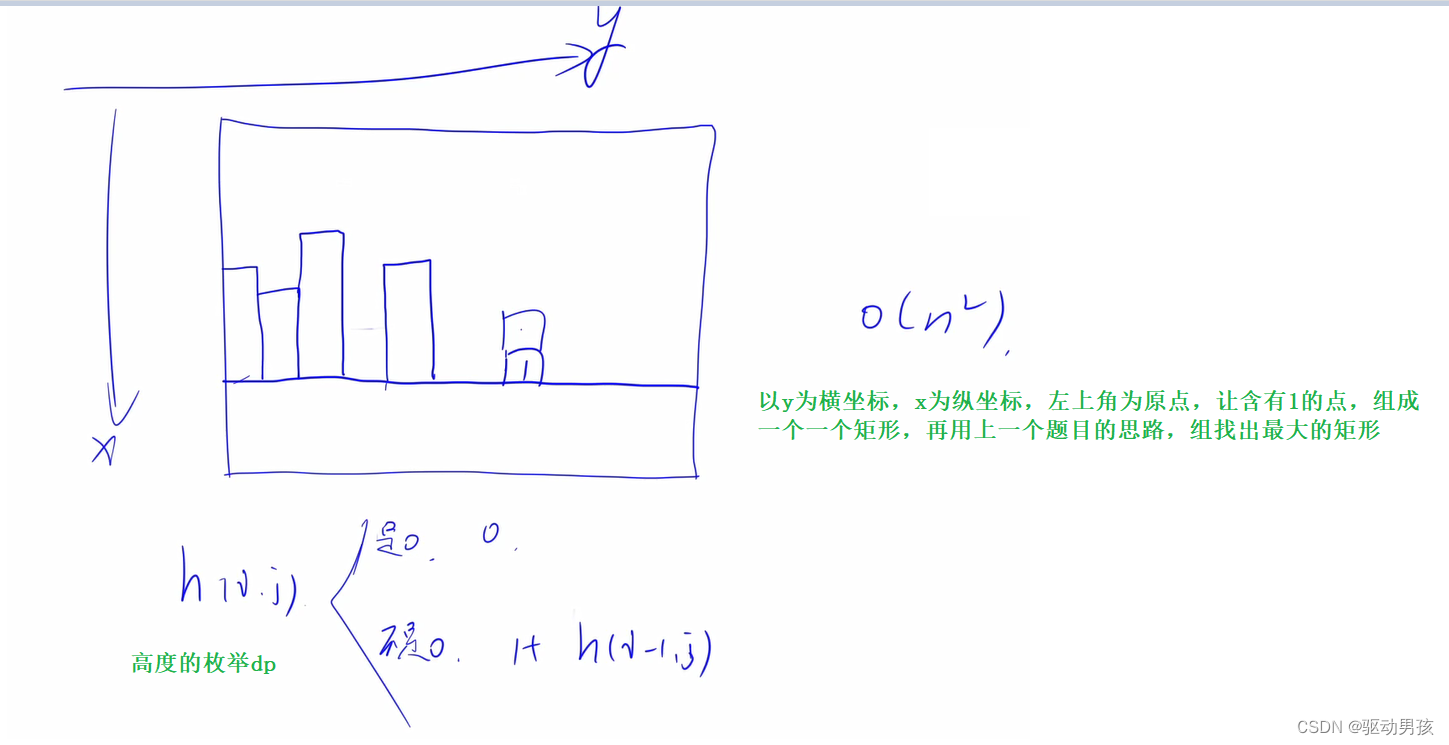
代碼

class Solution {
public:int largestRectangleArea( vector<int>& h ) {int n = h.size();vector<int> left( n ), right( n );stack<int> st;// 求每個矩形的第一個小于左邊界的矩形 - 用單調棧for ( int i = 0; i < n; ++i ) {while ( st.size() && h[st.top()] >= h[i] ) st.pop();if ( st.empty() ) left[i] = -1;else left[i] = st.top();st.push( i );}// 求每個矩形的第一個小于右邊界的矩形 - 用單調棧st = stack<int>(); // 清空棧for ( int i = n - 1; i >= 0; --i ) {while ( st.size() && h[st.top()] >= h[i] ) st.pop();if( st.empty() ) right[i] = n;else right[i] = st.top();st.push( i );}// 遍歷維護 最大值int ret = 0;for (int i = 0; i < n; ++i) ret = max( ret, (right[i] - left[i] - 1) * h[i] );return ret;}int maximalRectangle(vector<vector<char>>& matrix) {if(matrix.size() == 0 || matrix[0].size() == 0) return 0;int n = matrix.size(), m = matrix[0].size();// n 行， m 列vector<vector<int>> h(n,vector<int>(m));for(int i = 0; i < n; i ++) {for(int j = 0; j < m; j ++) {if(matrix[i][j] == '1') {if(i) h[i][j] = 1 + h[i - 1][j]; else h[i][j] = 1; } }}int ret = 0;// 把每行的矩形，按照上題的思路進行處理，然后維護最大值就好for(int i = 0; i < n; i ++) ret = max(ret, largestRectangleArea(h[i]));return ret;}
};