目錄
一、問題解析
二、實例剖析
三、算法思路
四、代碼實現
結果：
總結
前言
【問題】n 個作業{1, 2, …, n}要在兩臺機器上處理，每個作業必須先由機器 1 處理，再由機器 2 處理，機器 1 處理作業i所需時間為 ai，機器 2 處理作業 i 所需時間為 bi（1 ≤ i ≤ n），批處理作業調度問題（batch-job scheduling problem）要求確定這 n 個作業的最優處理順序，使得從第 1 個作業在機器 1 上處理開始，到最后一個作業在機器 2 上處理結束所需時間最少。
一、問題解析
【想法】顯然，批處理作業的一個最優調度應使機器 1 沒有空閑時間，且機器 2的空閑時間最小。
- 存在一個最優作業調度使得在機器 1 和機器 2 上作業以相同次序完成。
- 由于是一種作業調度順序的方案，因此該問題的解空間樹是排列樹。
二、實例剖析
例如，有三個作業{1, 2, 3}，在機器 1 上所需的處理時間為(2, 5, 4)，在機器 2上所需的處理時間為(3, 2, 1)，則存在 6 種可能的調度方案：{(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1)}，相應的完成時間為{12, 13, 12, 14, 13, 16}，最佳調度方案是(1, 2, 3)和(2, 1, 3)，最短完成時間為 12。
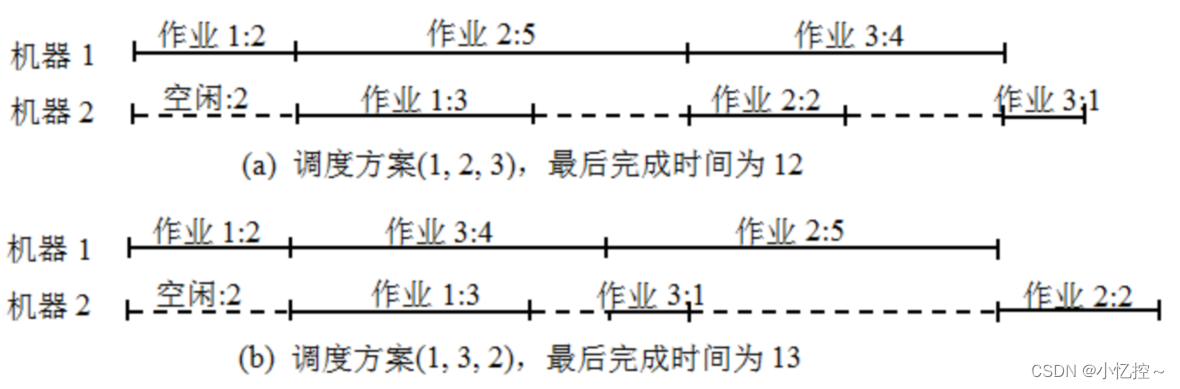
其他情況如上類似，這里就不再贅述！！
三、算法思路
【算法】設數組a[n]存儲 n 個作業在機器 1 上的處理時間，b[n]存儲 n 個作業在機器 2 上的處理時間。設數組x[n]表示 n 個作業批處理的一種調度方案，其中x[i]表示第 i 個處理的作業編號，sum1[n]和sum2[n]保存在調度過程中機器 1 和機器 2的當前完成時間，其中sum1[i]表示在安排第 i 個作業后機器 1 的當前完成時間，sum2[i]表示在安排第 i 個作業后機器 2 的當前完成時間，且根據下式進行更新：
關鍵點：
?sum1[i] = sum1[i-1] + a[ x[i] ]
?sum2[i] = max(sum1[i], sum2[i-1]） +b[ x[i] ]
算法：回溯法求解批處理調度BatchJob
輸入：n 個作業在機器 1 上的處理時間 a[n]，在機器 2 上的處理時間 b[n]
輸出：最短完成時間bestTime，最優調度序列 x[n]
1. 初始化解向量 x[n] = {-1}；最短完成時間bestTime = MAX;
2. 初始化調度方案中機器 1 和機器 2 的完成時間：
sum1[n] = sum2[n] = {0}; i = 0;
3. 當 i >= 0 時調度第 i 個作業：
3.1 依次考察每一個作業，如果作業 x[i] 尚未處理，則轉步驟 3.2，
否則嘗試下一個作業，即 x[i]++；
3.2 處理作業 x[i]：
3.2.1 ?sum1[i]=sum1[i-1]+ a[x[i]]；
3.2.2 ?sum2[i]=max{sum1[i], sum2[i-1]}+ b[x[i]]；
四、代碼實現
#include <iostream>
#include <vector>
#include <climits>using namespace std;int bestTime = INT_MAX;
vector<int> bestSchedule;
vector<int> currentSchedule;void backtrack(vector<int>& a, vector<int>& b, vector<bool>& processed, vector<int>& sum1, vector<int>& sum2, int index, int n) {if (index == n) {if (sum2[n-1] < bestTime) {bestTime = sum2[n-1];bestSchedule = currentSchedule;}return;}for (int i = 0; i < n; i++) {if (!processed[i]) {processed[i] = true;currentSchedule[index] = i;sum1[index] = (index > 0 ? sum1[index-1] : 0) + a[i];sum2[index] = max(sum1[index], (index > 0 ? sum2[index-1] : 0)) + b[i];backtrack(a, b, processed, sum1, sum2, index + 1, n);processed[i] = false;}}
}int batchJobScheduling(vector<int>& a, vector<int>& b) {int n = a.size();vector<bool> processed(n, false);vector<int> sum1(n, 0);vector<int> sum2(n, 0);currentSchedule.resize(n);backtrack(a, b, processed, sum1, sum2, 0, n);return bestTime;
}int main() {vector<int> a = {2, 3, 1};vector<int> b = {3, 1, 2};int result = batchJobScheduling(a, b);cout << "Best processing time: " << result << endl;cout << "Best schedule: ";for (int job : bestSchedule) {cout << job << " ";}cout << endl;return 0;
}結果：
第一行表示：所需的最短時間；第二行表示:最好的安排次序
總結
算法時間復雜度高，時間消耗太多了，在ACM上一直會超時，不如貪心法效率高。我是一個小菜雞，歡迎各路大神批評指正！！
?
)
