本篇會加入個人的所謂魚式瘋言

??????魚式瘋言:??????此瘋言非彼瘋言
而是理解過并總結出來通俗易懂的大白話,
小編會盡可能的在每個概念后插入魚式瘋言,幫助大家理解的.
🤭🤭🤭可能說的不是那么嚴謹.但小編初心是能讓更多人能接受我們這個概念 ！！！

前言

學習完了 雙指針算法，相比小伙伴應該對我們的 雙指針算法 爛熟于心了吧 💖 💖 💖

接下來迎面走來的就是我們的 == “滑動窗口” 算法== ,什么是滑動窗口算法，該怎么用，有哪些特殊的場景，下面就請寶子們和我一起推開 “滑動窗口” 算法的大門吧 💞 💞 💞

目錄

1. 滑動窗口的初識

2. 滑動窗口的應用

3. 滑動窗口的結論

一. 滑動窗口的初識

1. 滑動窗口的簡介

滑動窗口算法是一種常用的 解決字符串/數組子串問題 的算法。它通過維護一個窗口，該窗口在字符串/數組上滑動，每次滑動一個位置，并根據問題的要求調整窗口的 大小和位置 。

通過不斷滑動窗口，可以有效地解決 字符串/數組子串問題 。

滑動窗口算法的基本思想是通過兩個指針（左指針和右指針）來定義窗口的邊界。

2. 滑動窗口如何使用

初始時，左指針和右指針都指向字符串/數組的 第一個元素 ，然后右指針開始向右移動，直到滿足某個 條件（如子串的長度等）時停止。

然后左指針開始向右移動，同時 縮小窗口的大小，直到不滿足某個條件時停止。

這樣，通過不斷地向右移動 右指針 和 左指針，可以在 字符串/數組上 滑動窗口，并根據問題的要求進行相應的 調整和計算。

滑動窗口算法在求解字符串/數組子串問題時具有 高效性 ，因為它將問題的規模由 O(n^2) 降低到O(n) ，而且只需要遍歷一次 字符串/數組 。同時，滑動窗口算法也可以解決一些 其他類型的問題，

如求解最長不重復子串、找到滿足特定條件的子串等。

魚式瘋言

滑動窗口本質上還是一種 雙指針算法 ，

而我們滑動窗口的這個 “窗口” 其實就是雙指針所圍成的 一段區間

二. 滑動窗口的應用

1. 長度最小的子數組

長度最小的子數組題目鏈接

<1>. 題目描述

給定一個含有 n 個正整數的數組和一個正整數 target 。

找出該數組中滿足其和 ≥ target 的長度最小的 連續子數組 [numsl, numsl+1, …,
numsr-1, numsr] ，并返回其長度。如果不存在符合條件的子數組，返回 0 。

示例 1：
輸入： target = 7, nums = [2,3,1,2,4,3]
輸出： 2
解釋：
子數組 [4,3] 是該條件下的長度最小的子數組。

示例 2：
輸入： target = 4, nums = [1,4,4]
輸出： 1

示例 3：
輸入： target = 11, nums = [1,1,1,1,1,1,1,1]
輸出： 0

題目含義:

找到一群 最短 連續的元素，這群元素之和大于等于 我們的目標值 target

<2>. 講解算法思想

當我們看到這道題時，我們是需要兩個數來充當我們的 左邊界 和 右邊界 的

解法一:

暴力枚舉

我們就可以通過先 固定左邊界 的值，來移動右邊界 的方式來查找我們需要的最小子數組的長度

解法二 ：

滑動窗口

我們在解法一的基礎上優化出 “滑動窗口” 的算法思路

滑動窗口算法的 三步驟 ：

先

用定義兩個指針 left 和 right 讓我們都指向 零位置

入窗口操作

先讓 right 不斷向右移動， 并用 sum 來計算滑動窗口內的總和

出窗口操作

當我們 sum 滿足 >= target 時， 我們就讓 left 也 向右移動，同時 sum 減去 left
位置的值

更新結果

當我們 每次滿足 sum >= right 時，就 更新 每次的長度，直到找到 最小 的那個長度為止

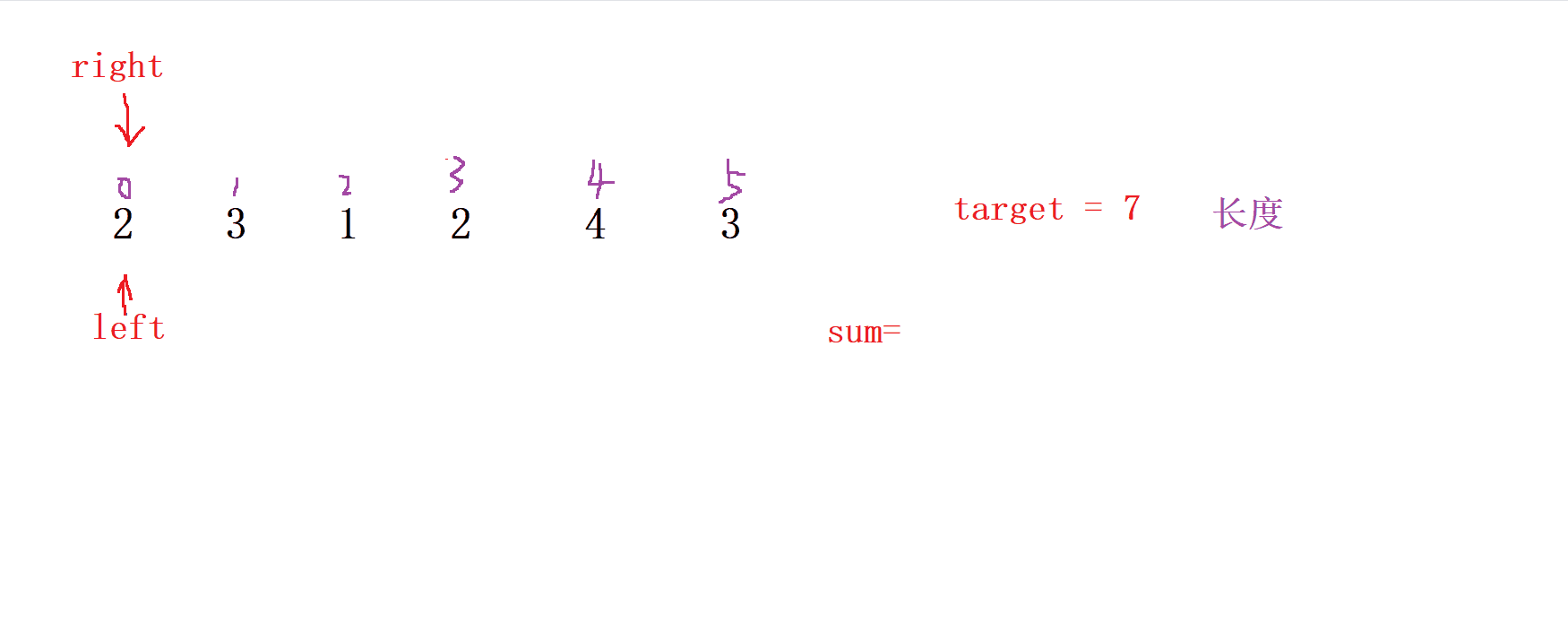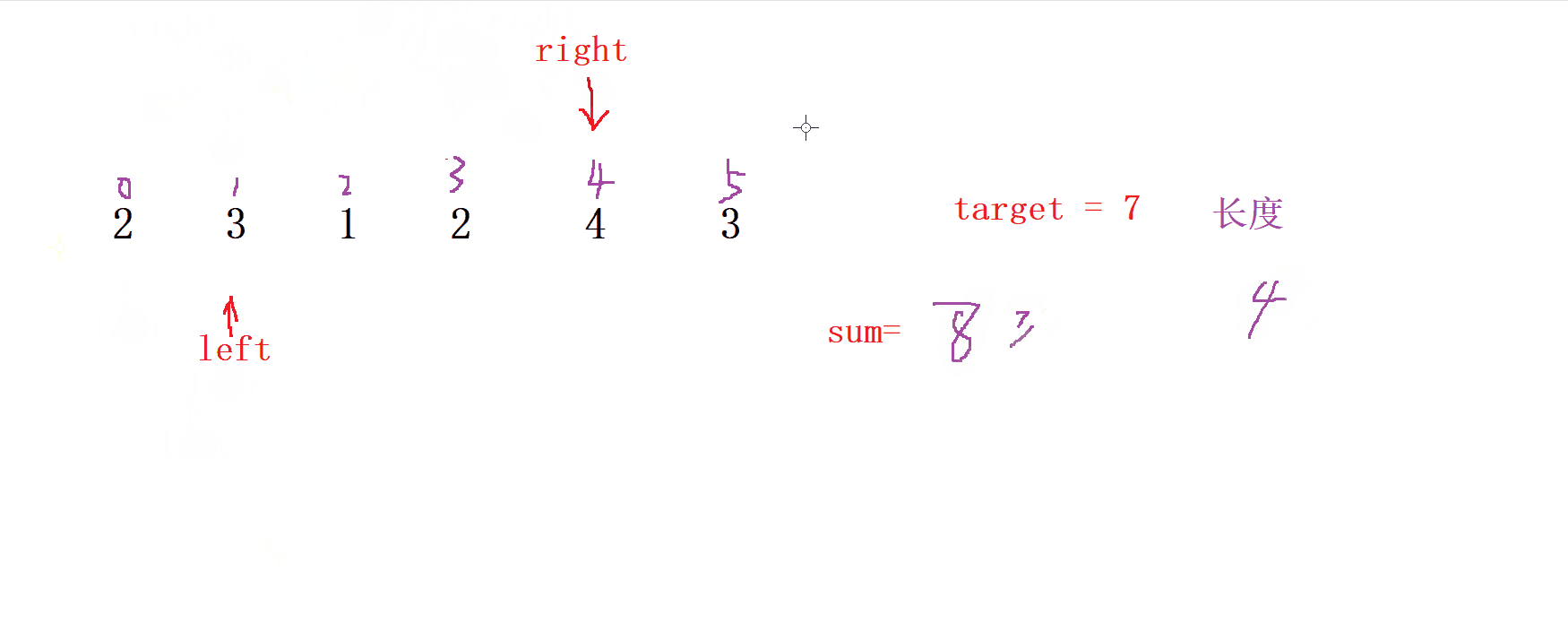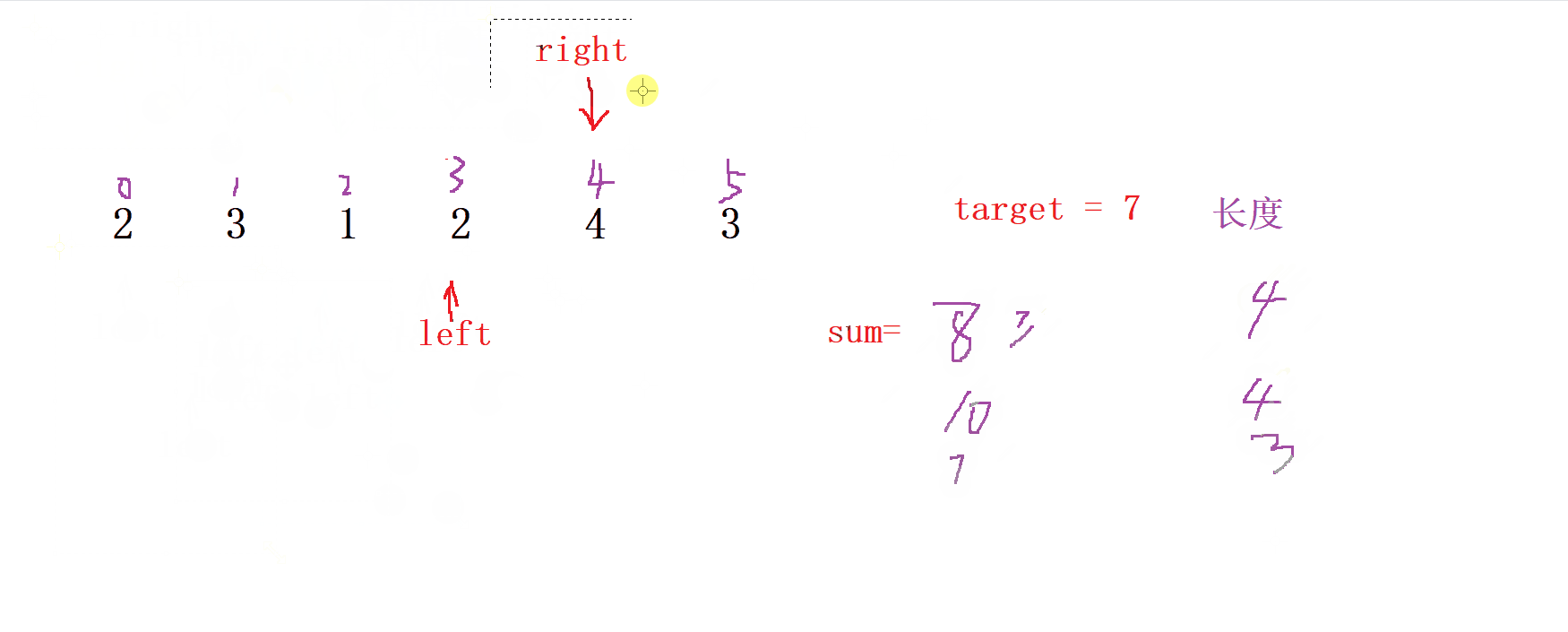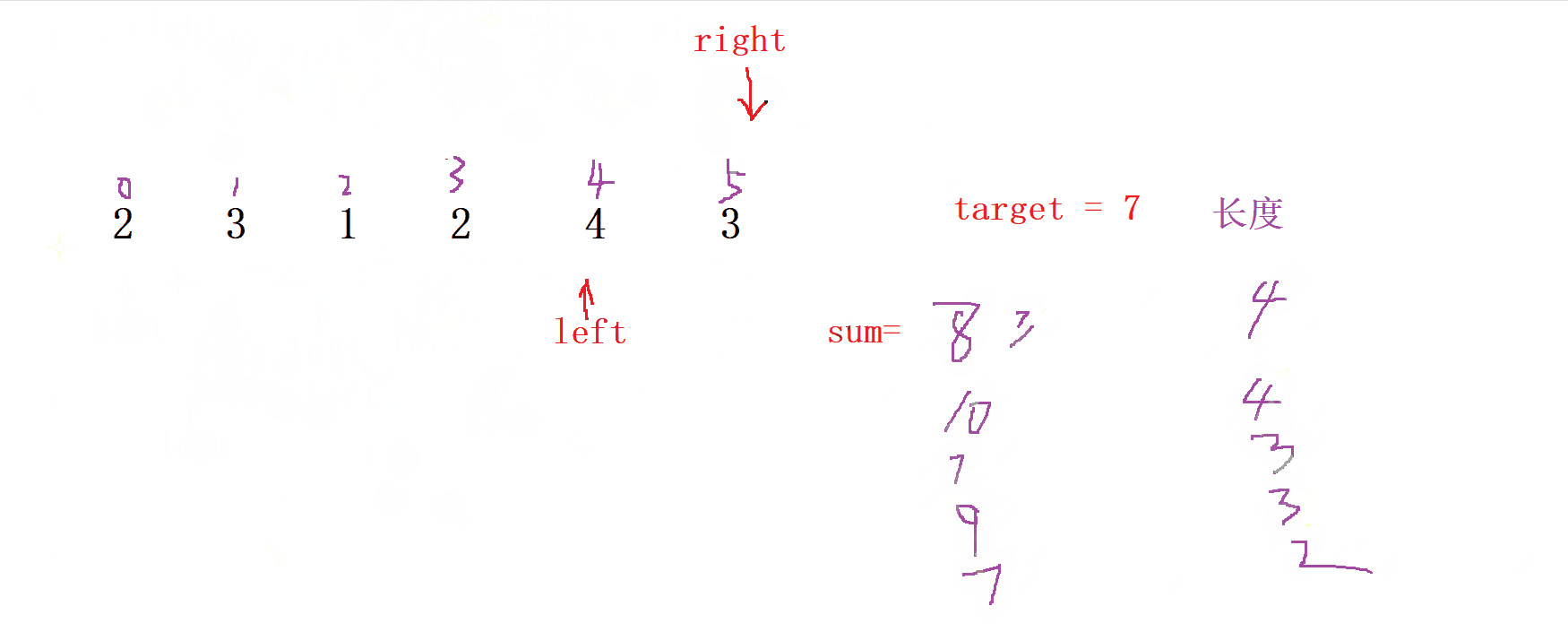
<3>. 編寫代碼

class Solution {public int minSubArrayLen(int target, int[] nums) {int sz=nums.length;int left=0,right=0;int sum=0,len=Integer.MAX_VALUE;for( ;right< sz;right++) {sum += nums[right];while(sum >= target) {len= Math.min(len,right-left+1);sum -= nums[left];left++;}}return len > sz ? 0: len;}
}

魚式瘋言

說兩點小編自己的體會

1. 在我們的滑動窗口算法中 ， right 不需要回退 的，當我們需要改變 “窗口” 的狀態時， 唯一要看的是條件需要什么，來移動我們的 left 的位置來調整

 for( ;right< sz;right++) { }

2. 終止條件的判定，我們只需要讓 right 走完整個數組 即可 ，因為這個 滑動的 “窗口” 存在 于 有實際含義的區域

當 right 出了數組，也就意味著 滑動窗口 就不存在了

2. 最大連續1 的個數

1004.最大連續 1 的個數 題目鏈接

<1>. 題目描述

給定一個二進制數組 nums 和一個整數 k，如果可以翻轉最多 k 個 0 ，則返回 數組中連續 1 的最大個數 。

示例 1：

輸入：nums = [1,1,1,0,0,0,1,1,1,1,0], K = 2
輸出：6
解釋：[1,1,1,0,0,1,1,1,1,1,1]
粗體數字從 0 翻轉到 1，最長的子數組長度為 6。

示例 2：

輸入：nums = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
輸出：10
解釋：[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
粗體數字從 0 翻轉到 1，最長的子數組長度為 10。

題目含義:

尋找一段連續有 1 的數組，如果存在 零 的話，并可以補最多 k 個零 的最長子數組

<2>. 講解算法思想

題目分析 ：

我們需要的是 1 的長度，但是 1 卻有可能會加入 0

那我們不妨從 正難則反 的思維來統計 零 出現的個數

當 零的個數 <= k 的時候就統計長度， 當 > k 時候，我們就減少零的個數

解法一 :

暴力枚舉

還是兩個 for 的嵌套 ，一端固定 ，一端移動，并且通過 滿足 零 個數時候的 子數組的長度

解法二 ：

滑動窗口

還是先 定義兩個指針 ，left，right 都指向 0 下標的位置

入窗口操作

讓 right 一直 向右 移動 ，并用 zero 來統計 出現過的 零 的個數， 只要 零 的個數 <= k

我們就一直入窗口

出窗口

當 zero 的個數 > k 時，就讓 left ++ 向右移動 , 直到 zero <= k 時，停止 出窗口

更新結果

只要 零 的個數 <= k , 我們就不斷更新結果，直到找到我們 最長的子數組

<3>. 編寫代碼

class Solution {public int longestOnes(int[] nums, int k) {int sz=  nums.length;if(k >= sz) return sz;int sum=0,zero=0;int ret=0;for(int left=0, right=0; right < sz ;right++) {// 統計 0 的個數來進窗口if(nums[right] == 0) {zero++;}// 通過 0 的個數和 k的大小比較 來出窗口while(zero > k) {if(nums[left]==0) {zero--;}left++;}ret=Math.max(right-left+1,ret);}                                                                                                                                                                                       return ret;}}

魚式瘋言

小編這里最想強調的一點就是我們 這個解題的思維

這個思路： 正難則反

題目要求是統計 1出現的子數組的長度

當我們只需要從 反面 來統計 出現 零的個數， 進行 滑動窗口的 出 和 入

3. 最小覆蓋子串

76.最小覆蓋子串題目鏈接

<1>. 題目描述

給你一個字符串 s 、一個字符串 t 。返回 s 中涵蓋 t 所有字符的最小子串。如果 s 中不存在涵蓋 t 所有字符的子串，則返回空字符串 “” 。

注意：

對于 t 中重復字符，我們尋找的子字符串中該字符數量必須不少于 t 中該字符數量。
如果 s 中存在這樣的子串，我們保證它是唯一的答案。

示例 1：

輸入：s = “ADOBECODEBANC”, t = “ABC”
輸出：“BANC”
解釋：最小覆蓋子串 “BANC” 包含來自字符串 t 的 ‘A’、‘B’ 和 ‘C’。

示例 2：

輸入：s = “a”, t = “a”
輸出：“a”
解釋：整個字符串 s 是最小覆蓋子串。

示例 3:

輸入: s = “a”, t = “aa”
輸出: “”
解釋: t 中兩個字符 ‘a’ 均應包含在 s 的子串中，
因此沒有符合條件的子字符串，返回空字符串。

** 題目含義**

給定一個字符串 s，得到所有包含 t 每一個的子串的 下標

<2>. 講解算法思想

當我們分析這題時，肯定少不了要統計 字符串中每個字符出現的 個數 ，這時我們就需要 借用一個工具 來使用

那就是我們的 哈希表💞 💞 💞

本題解法：

滑動窗口 + 哈希表

算法步驟

1. 先定義兩個哈希表 hash1 和 hash2 分別統計 s 和 t 中出現字符的個數

2. 先把 t 中 的每個字符都存入到哈希表 hash1 中

入窗口

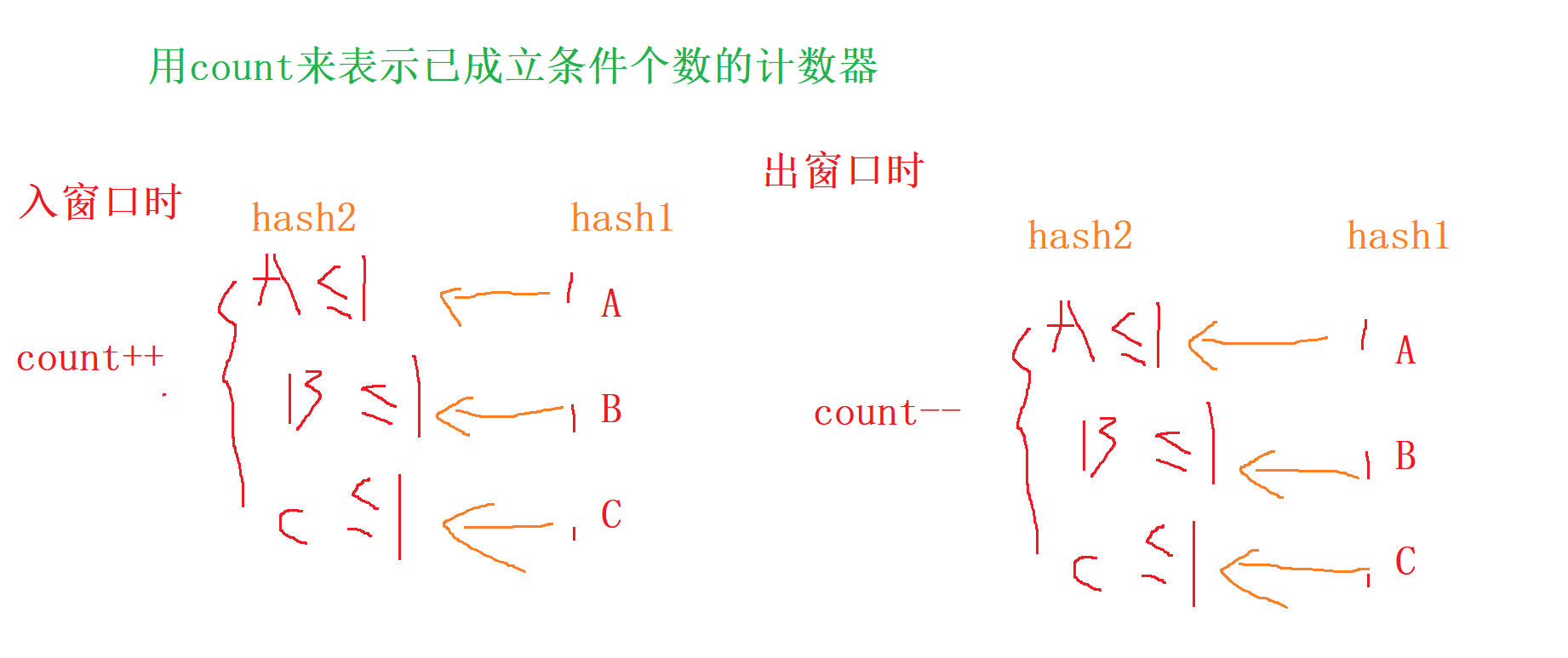
3. 然后再 用 滑動窗口 ，先讓 right 一直往右走， 一直進入哈希表 ， 當 hash2 【A】 <= hash1 【A】 (其他字符以此類推) ， 我們就用count 來統計增加的個數， 否則 count 不變

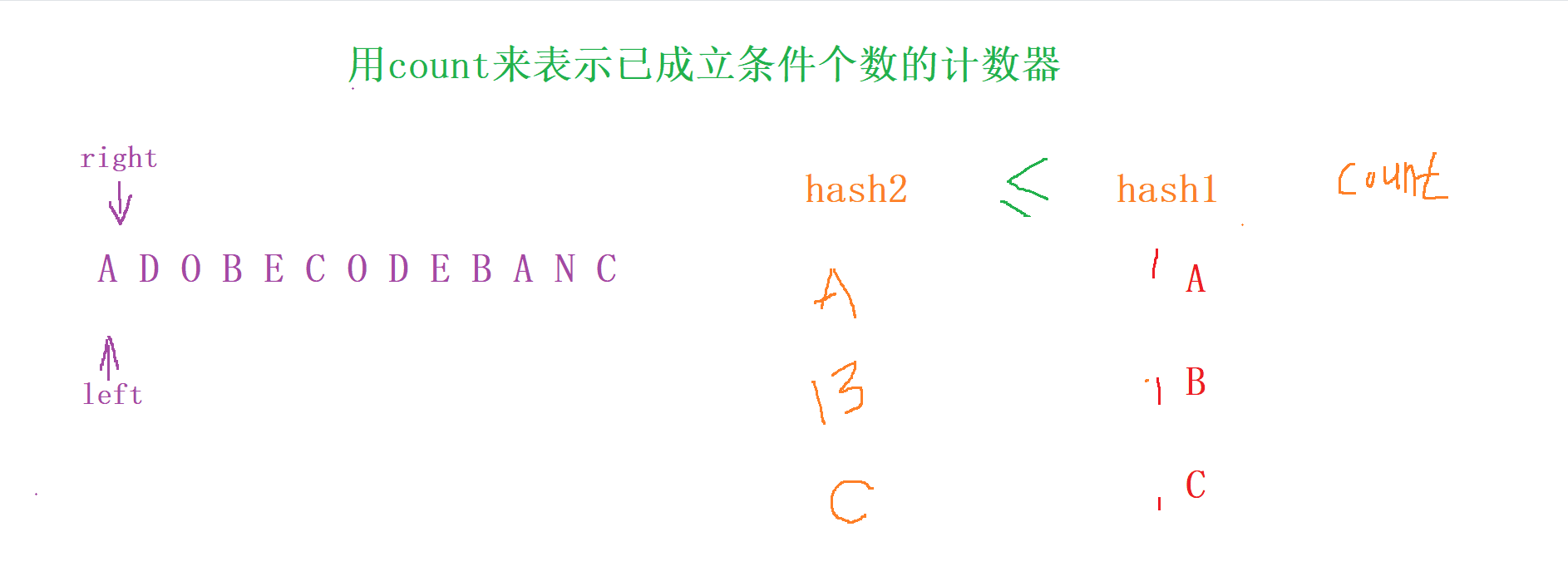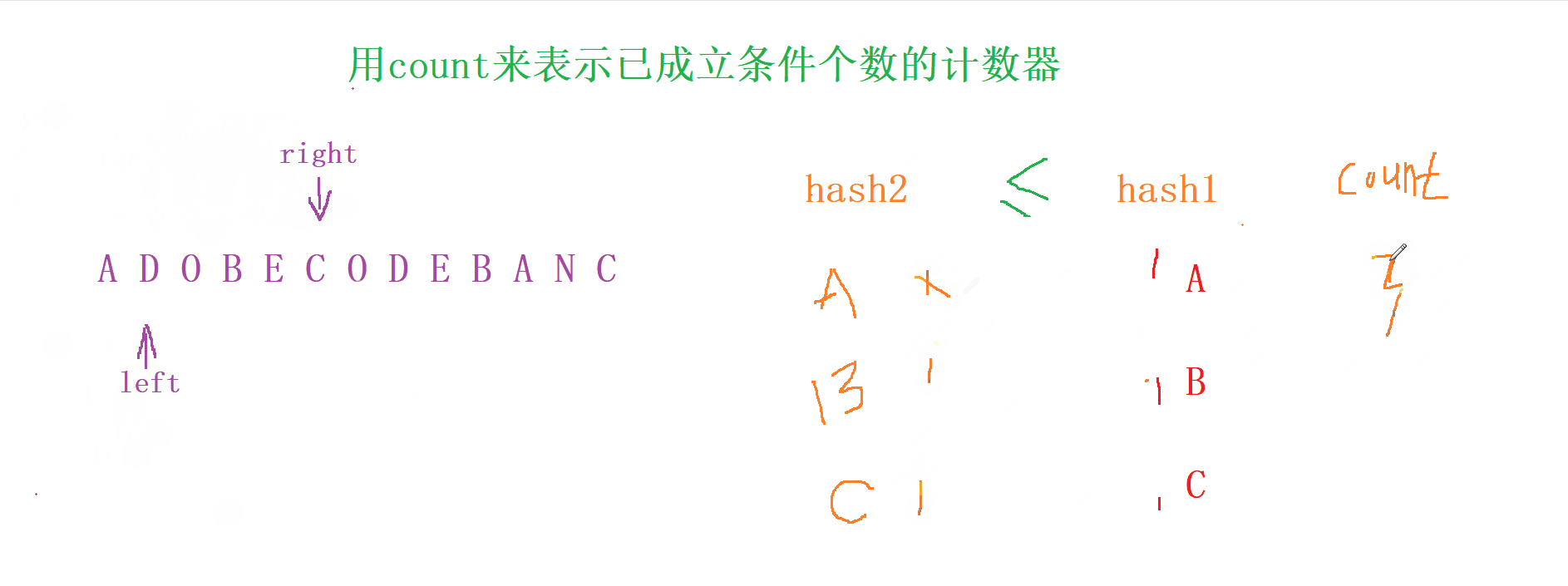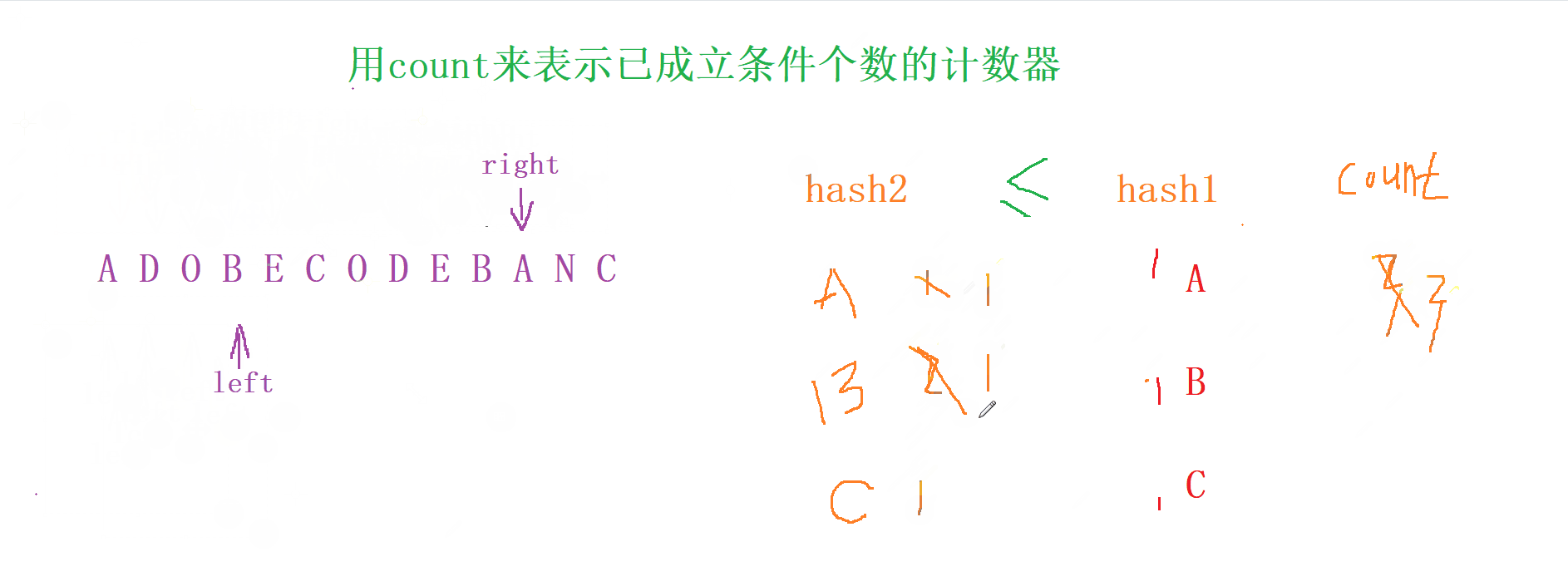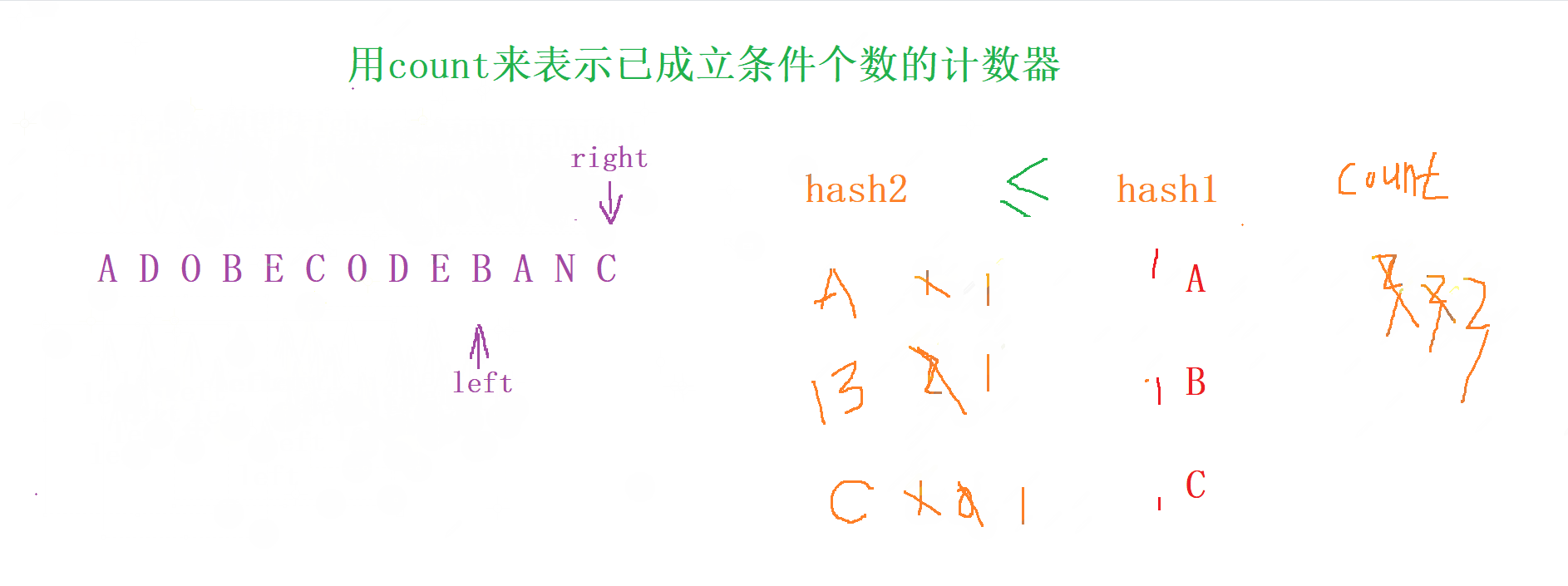
更新結果

當 count 的值 = 數組長度 時 ， 我們就 更新結果，記錄當前 下標

出窗口操作

先 去除 hash2 中 left 當前下標的字符

如果我們的 當 hash2 【A】 <= hash1 【A】 (其他字符以此類推) ， 我們就用count 來 減少成立的個數， 否則 count 不變

<3>. 編寫代碼

class Solution {public String minWindow(String s, String t) {// 先得到兩個字符串的長度int slength=s.length();int  tlength=t.length();// 先定義兩個數組來哈希映射 統計次數int [] hash1= new int[100];int [] hash2= new int[100];// 先統計 s 中 字符的個數for(int i=0; i < tlength ; ++i) {hash1[t.charAt(i)-'A']++;}int len = Integer.MAX_VALUE;int begin=Integer.MAX_VALUE;// 進行滑動窗口操作for(int left=0,right=0, count=0; right < slength ; right++) {// 入窗口char in= s.charAt(right);hash2[in-'A']++;// 判斷if(hash2[in-'A'] <= hash1[in-'A']) {count++;}// 更新結果while(count == tlength) {// 得到最小長度 并記錄起始位置if(right-left+1 < len) {begin=left;len=right-left+1; }char out= s.charAt(left);// 出窗口if(hash2[out-'A'] <= hash1[out-'A']) {count--;}hash2[out-'A']--;left++;} }// 不存在直接返回空字符串if(begin==Integer.MAX_VALUE) return "";// 截斷時要注意 左閉右開// 當起始位置加上 字符串長度時// 不需要 -1return s.substring(begin,begin+len);}
}

魚式瘋言

對于本題,小編這里有 三點體會 和小伙伴們一起分享

1. 當我們需要對滑動窗口進行 出窗口 還是 入窗口 判斷時， 用 count 來統計是否成立的 字符的個數 這個思想是很巧妙的

2. 當我們需要統計一個字符串中出現 所有字符的情況 的時候， 哈希表 是不錯的工具

3. 在這里,.我們看到了更新結果的位置是在 入窗口 和出窗口 之間, 上題中我們的更新結果是在 出窗口之后, 所以我們的更新結果是 不固定 有可能在 入窗口和出窗口之間 , 也有可能在 == 出窗口 之后==

4. 串聯所有單詞的子串

30.串聯所以單詞的子串題目鏈接

<1>. 題目描述

給定一個字符串 s 和一個字符串數組 words。 words 中所有字符串 長度相同。

s 中的 串聯子串 是指一個包含 words 中所有字符串以任意順序排列連接起來的子串。

例如，如果 words = [“ab”,“cd”,“ef”]， 那么 “abcdef”， “abefcd”，“cdabef”， “cdefab”，“efabcd”，

和 “efcdab” 都是串聯子串。 “acdbef” 不是串聯子串，因為他不是任何 words 排列的連接。

返回所有串聯子串在 s 中的開始索引。你可以以 任意順序 返回答案。

示例 1：

輸入：s = “barfoothefoobarman”, words = [“foo”,“bar”]

輸出：[0,9]

解釋：因為 words.length == 2 同時 words[i].length == 3，連接的子字符串的長度必須為 6。

子串 “barfoo” 開始位置是 0。它是 words 中以 [“bar”,“foo”] 順序排列的連接。

子串 “foobar” 開始位置是 9。它是 words 中以 [“foo”,“bar”] 順序排列的連接。

輸出順序無關緊要。返回 [9,0] 也是可以的。

示例 2：

輸入：s = “wordgoodgoodgoodbestword”, words = [“word”,“good”,“best”,“word”]

輸出：[]

解釋：因為 words.length == 4 并且 words[i].length == 4，所以串聯子串的長度必須為 16。
s 中沒有子串長度為 16 并且等于 words 的任何順序排列的連接。
所以我們返回一個空數組。

示例 3：

輸入：s = “barfoofoobarthefoobarman”, words = [“bar”,“foo”,“the”]
輸出：[6,9,12]

解釋：因為 words.length == 3 并且 words[i].length == 3，所以串聯子串的長度必須為 9。

子串 “foobarthe” 開始位置是 6。它是 words 中以 [“foo”,“bar”,“the”] 順序排列的連接。

子串 “barthefoo” 開始位置是 9。它是 words 中以 [“bar”,“the”,“foo”] 順序排列的連接。

子串 “thefoobar” 開始位置是 12。它是 words 中以 [“the”,“foo”,“bar”] 順序排列的連接。

題目含義 :

找到所有完全包含 words 的字符子串（不包含 每個單詞 的順序，一定是包含 單詞內每個字符 的順序）

<2>. 講解算法思想

題目分析:

本題目的是找到相同的 子字符串 ， 而且是不按照順序的 ，所以我們 還得借用我們的 哈希表 這個工具來完成本題

算法步驟

首先得到 還是定義 一個 left 和 right 來進行 滑動窗口的 操作， 并且定義 兩個哈希表 hash1 和 hash2 來分別統計 words 和 s 的字符串 出現的次數。

入窗口

我們先讓 right 嗎，以每個 單詞的長度 為單位進行移動 ， 截取該 單詞長度的子字符串 進入 哈希表

3. 用 滑動窗口 ，先讓 right 一直往右走， 一直進入哈希表 ， 當 hash2 【foo】 <= hash1 【foo】 (其他字符以此類推) ， 我們就用count 來統計增加的個數， 否則 count 不變

更新結果

一旦 count 滿足 字符串數組中所有字符 的總和長度

我們就 更新結果 ,存放該 left 的下標

出窗口操作

當 count 滿足 字符串數組 長度

更新完結果后， 我們就讓 left 也跟著 每個單詞(子字符串) 想右移動進行 出窗口 的操作

最后讓重新初始化我們的 left 繼續每次向右 移動 一格， 只需要 循環移動 每個 子字符串的長度 即可

<3>. 編寫代碼

class Solution {public  List<Integer> findSubstring(String s, String[] words) {// 得到每個 字符串以及字符串數組的長度int slen=s.length();int wdslen=words.length;int wlen= words[0].length();// 定義一個返回結果List<Integer> ret= new ArrayList<>();// 先 定義兩個 hashMap// 用于統計 字符串 的數量Map<String, Integer>  hash1= new HashMap<>();// 統計 words 里面 的長度for(int i=0; i< wdslen ; i++) {String str= words[i];hash1.put(str,hash1.getOrDefault(str,0)+1);}// 開始進行滑動窗口操作for(int j=0; j < wlen ; ++j) {Map<String, Integer>  hash2= new HashMap<>();// 初始化 left 和 right 的最初位置int  left=j;int right= j + wlen;int count=0;// 設置  right 每次跳躍的 跨度for( ;right  <= slen ; right += wlen) {// 通過入窗口操作String in = s.substring(right-wlen,right);hash2.put(in,hash2.getOrDefault(in,0)+1);// 判斷有效結果if(hash1.containsKey(in) && hash2.get(in).compareTo(hash1.get(in)) <= 0) {count++;}// 判斷是否存在while(count >= wdslen) {// 更新結果if(right-left ==  wdslen * wlen) {ret.add(left);}String out= s.substring(left,left+wlen);// 出窗口操作if(hash1.containsKey(out) && hash2.get(out).compareTo(hash1.get(out)) <= 0) {count--;}// 更新每次 left 跳躍的值hash2.put(out,hash2.get(out)-1);left += wlen;}}}return ret;}
}

魚式瘋言

以上的整體的思路小編就介紹的差不多，但還有細節問題需要處理

 // 通過入窗口操作String in = s.substring(right-wlen,right);

1. 注意這個字符串截取的方法 是 左閉右開 區間，就意味著右邊的 下標位置是取不到的

 // 出窗口操作if(hash1.containsKey(out) && hash2.get(out).compareTo(hash1.get(out)) <= 0) {count--;}

2. 首先要包含這個字符串，其次就是當我們 比較兩個字符串大小 的時候，不能用 == 來比較，只能用 compareTo（） 來比較兩個字符串的大小關系

  // 更新結果if(right-left ==  wdslen * wlen) {ret.add(left);}

3. 更新結果的時候，我們獲取的是 全部單詞長度的總和 ， 所以 是和 wdslen * wlen 進行比較大小的

三. 滑動窗口的結論

通過文章的學習

• 在滑動窗口的初識 中

我們先是認識到 滑動窗口 本質上就是 兩個 指針所圍成的區域

而我們通過這個調整這個 區域 來 解決算法問題的方式就是叫 滑動窗口算法

• 在 滑動窗口的應用 中

我們在 長度最小數組 和 最大連續1 的個數中, 見識到了如何根據我們需要的條件來 入窗口 和出窗口
調整滑動窗口的方法來解決我們 一段有單調性并且連續的子數組 或者 子字符串 的問題

而我們又在 “最小覆蓋子串” 和 “串聯所有單詞的子串” 中， 通過 以 滑動窗口 和 哈希表 的思想共同
解決我們的 ***包含該元素卻是無序的情況 *** 的一種算法問題 。

如果覺得小編寫的還不錯的咱可支持 三連 下 (定有回訪哦) , 不妥當的咱請評論區 指正

希望我的文章能給各位寶子們帶來哪怕一點點的收獲就是 小編創作 的最大 動力 💖 💖 💖