二叉樹
1、什么是二叉樹
二叉樹(Binar Tree)是n(n>=0)個結點的優先集合,該集合或者為空集(稱為空二叉樹),或者由一個根結點和兩顆互不相交的、分別稱為根結點的左子樹和右子樹的二叉樹構成。
這里給張圖,能更直觀的感受二叉樹:
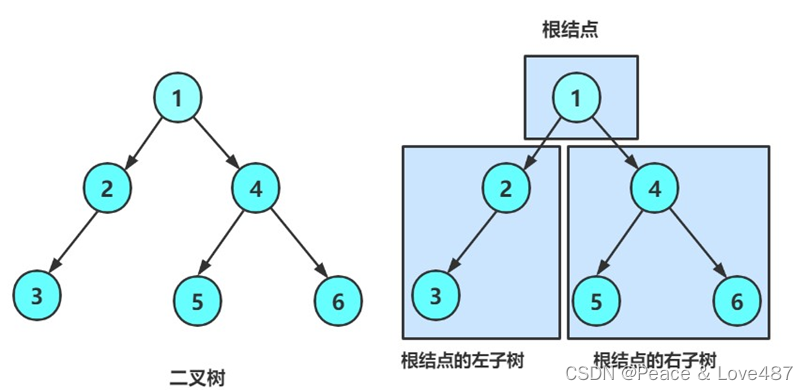
? 2、二叉樹的特點
從上圖可以看出二叉樹的幾個特點:
- 二叉樹不存在度大于2的結點,每個結點最多有兩顆子樹;
- 左子樹和右子樹是有順序的,次序不能顛倒;
- 即使樹中的某個結點只有一顆子樹,那也要區分它是左子樹還是右子樹。
講到這那就不得不提及二叉樹的五種基本形態:
- 空二叉樹;
- 只有一個根節點;
- 根結點只有左子樹;
- 根結點只有右子樹;
- 根結點既有左子樹又有右子樹。

?
如下圖所示,這棵樹就不符合二叉樹的條件,所以它就不是一顆二叉樹。
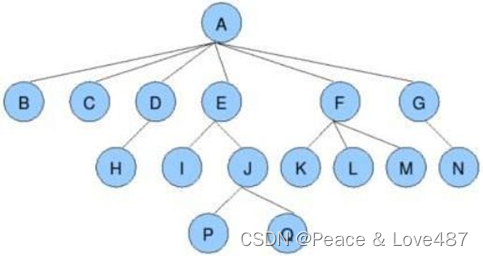
?
3、幾種特殊的二叉樹
- 斜樹:顧名思義,斜樹一定是要斜的,但是往哪斜是有講究的。所有結點只有左子樹的二叉樹叫左斜樹。所有結點只有右子樹的二叉樹叫右斜樹。這兩者統稱為斜樹。

- 滿二叉樹:在一棵二叉樹中,如果所有分支結點都存在左子樹和右子樹,并且所有葉子都在同一層上,這樣的二叉樹稱為滿二叉樹。
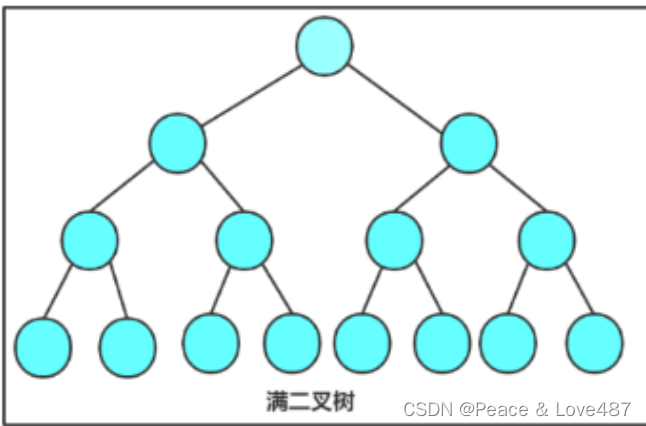
- 完全二叉樹:完全二叉樹是效率很高的數據結構,完全二叉樹是由滿二叉樹而引出來的。對于深度為K的,有n個結點的二叉樹,當且僅當其每一個結點都與深度為K的滿二叉樹中編從1至n的結點一一對應時稱之為完全二叉樹。 要注意的是滿二叉樹是一種特殊的完全二叉樹。
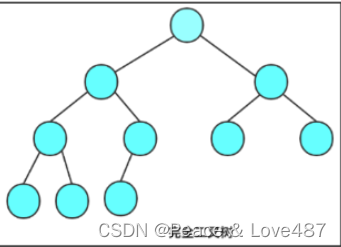
?
4、二叉樹的性質
4.1 滿二叉樹的性質
- 葉子只能出現在最下一層。出現在其他層就不可能達到平衡;
- 非葉子節點的度一定是2,否則就是“缺胳膊少腿”了;
- 在同樣深度的二叉樹中,滿二叉樹的結點個數最多,葉子最多。
4.2 完全二叉樹的性質
- 葉子結點只能出現在最下兩層;
- 最下層的葉子一定集中在左部連續位置;
- 倒數兩層,若有葉子結點,一定都在右部連續位置;
- 如果結點度為1,則該結點只有左孩子,即不存在只有右孩子的情況;
- 同樣結點數的二叉樹,完全二叉樹的深度最小。
4.3 二叉樹的性質
- 若規定根節點的層數為 1 ,則一棵非空二叉樹的 第 i 層上最多有2^(i-1)?個結點.
- 若規定根節點的層數為1,則深度為h的二叉樹的最大結點數是2^h - 1.
- 若規定根節點的層數為 1 ,具有 n 個結點的滿二叉樹的深度 , h= log2(n+1). (ps:是log 以 2 為底,n+1 為對數 ).
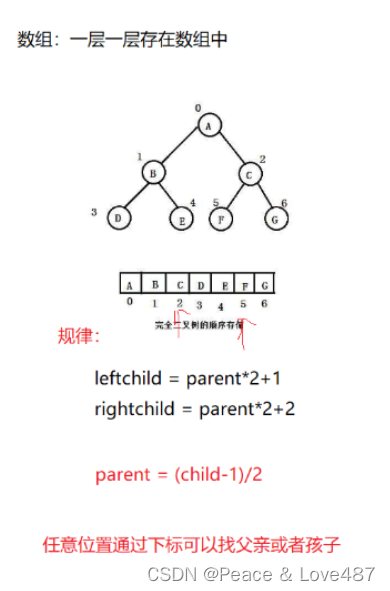
- 對于具有n個結點的完全二叉樹,如果按照從上至下從左至右的數組順序對所有節點從0開始編號,則對 于序號為i的結點有:1. 若 i>0 , i 位置節點的雙親序號: (i-1)/2 ; i=0 , i 為根節點編號,無雙親節點2. 若 2i+1<n ,左孩子序號: 2i+1 , 2i+1>=n 否則無左孩子3. 若 2i+2<n ,右孩子序號: 2i+2 ,2i+2>=n否則無右孩子
- 對任何一棵二叉樹, 如果度為 0 其葉結點個數為n0? , 度為 2 的分支結點個數為n2? , 則有 n0=n2?+ 1.
5、現實中的二叉樹

6、二叉樹的存儲結構
二叉樹一般可以使用兩種存儲結構,一種是順序存儲結構,另一種則是鏈式存儲結構。?
6.1 順序存儲結構
二叉樹的順序存儲結構計算用一個一維數組存儲二叉樹中的結點。一般使用數組只適合表示完全二叉樹,因為不是完全二叉樹會有空間的浪費。而現實中使用中只有堆才會使用數組來存儲。
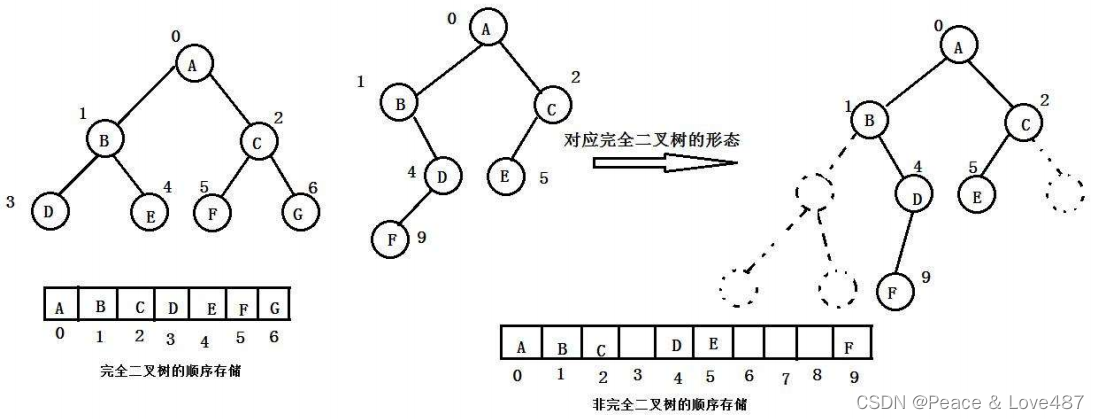
6.2 鏈式存儲結構
二叉樹的鏈式存儲結構是指,用鏈表來表示一棵二叉樹,即用鏈來指示元素的邏輯關系。 通常的方法是鏈表中每個結點由三個域組成,數據域和左右指針域,左右指針分別用來給出該結點左孩子和右孩子所 在的鏈結點的存儲地址 。鏈式結構又分為二叉鏈和三叉鏈。
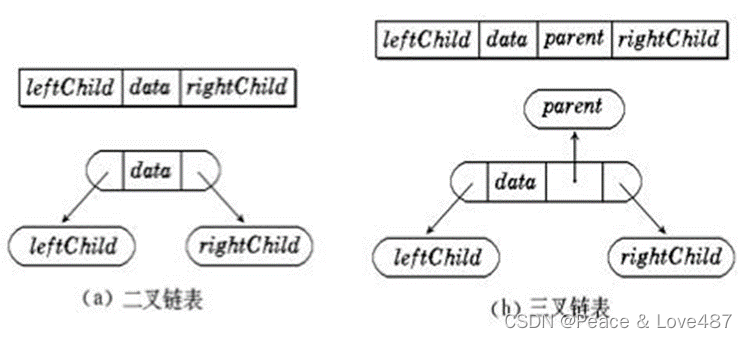
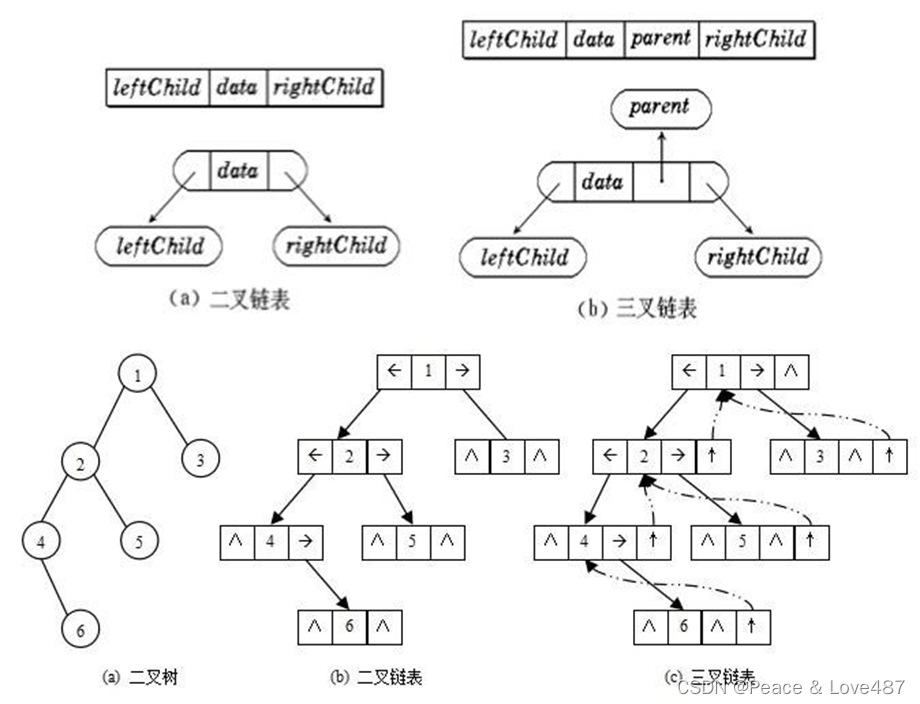
?
typedef int BTDataType;
// 二叉鏈
struct BinaryTreeNode
{struct BinTreeNode* _pLeft; // 指向當前節點左孩子struct BinTreeNode* _pRight; // 指向當前節點右孩子BTDataType _data; // 當前節點值域
}
// 三叉鏈
struct BinaryTreeNode
{struct BinTreeNode* _pParent; // 指向當前節點的雙親struct BinTreeNode* _pLeft; // 指向當前節點左孩子struct BinTreeNode* _pRight; // 指向當前節點右孩子BTDataType _data; // 當前節點值域
};?
7、二叉樹的順序存儲結構
普通的二叉樹是不適合用數組來存儲的,因為可能會存在大量的空間浪費。而完全二叉樹更適合使用順序結 構存儲。現實中我們通常把堆 ( 一種二叉樹 ) 使用順序結構的數組來存儲,需要注意的是這里的堆和操作系統 虛擬進程地址空間中的堆是兩回事,一個是數據結構,一個是操作系統中管理內存的一塊區域分段。
7.1 堆的概念和結構
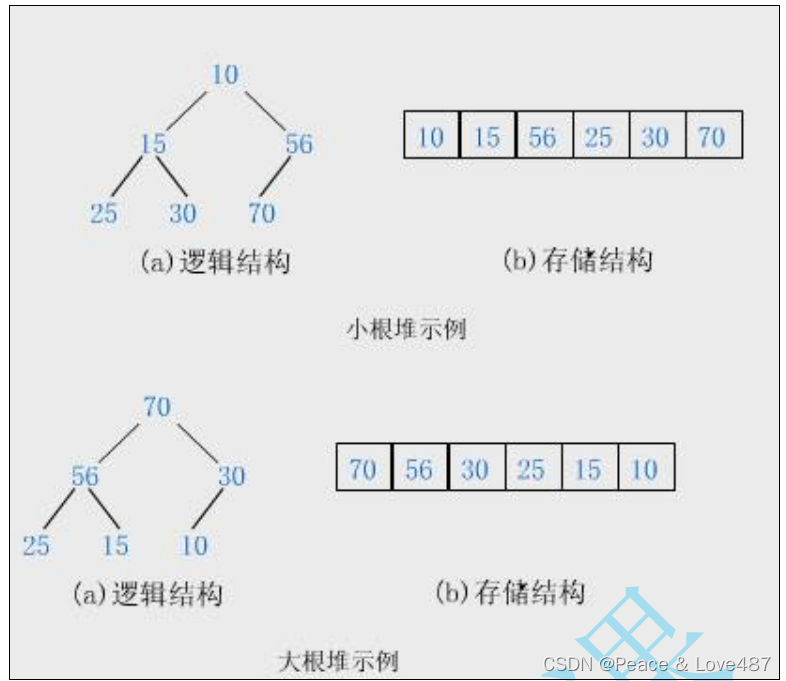
如果有一個關鍵碼的集合 K = { k0 ,k1 ,k2 , … ,kn-1},把它的所有元素按完全二叉樹的順序存儲方式存儲 在一個一維數組中,并滿足:?ki<=k2i+2 且 ki<=k2i+1?(ki >=k2i+1 且?ki>=k2i+2 ) i = 0, 1, 2…,則稱為小堆 ( 或大堆 ) 。將根節點最大的堆叫做最大堆或大根堆,根節點最小的堆叫做最小堆或小根堆。
堆的性質:
堆中某個節點的值總是不大于或不小于其父節點的值;
堆總是一棵完全二叉樹。
?
?
7.2 堆的實現
?實現堆的接口函數:
?
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include<time.h>
#include<string.h>typedef int HPDataType;
typedef struct Heap
{//數組存儲HPDataType* a; //數組int size; //數據的個數int capacity; //數組長度
}HP;//初始化
void HeapInit(HP* php);//釋放空間
void HeapDestory(HP* php);//插入數據
void HeapPush(HP* php, HPDataType x);//打印數據
void HeapPrint(HP* php);//刪除數據
void HeapPop(HP* php);//獲取第一個數據
HPDataType HeapTop(HP* php);//判斷是否為空
bool HeapEmpty(HP* php);函數的具體實現
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->size = php->capacity = 0;
}//釋放空間
void HeapDestory(HP* php)
{assert(php);free(php->a);php->a = NULL;php->size = php->capacity = 0;
}//交換數據
void Swap(HPDataType* x, HPDataType* y)
{HPDataType tmp = *x;*x = *y;*y = tmp;
}//結點向上調整 -- 小堆
void AdJustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//循環判定條件為孩子結點下標大于0while (child > 0){ //如果孩子結點值小于父親節點就相互交換if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}//如果孩子結點值大于或等于父親節點值就直接跳出循環else{break;}}}//向下調整
void AdJustDown(HPDataType* a, int n, int parent)
{int child = 2 * parent + 1;while (child < n ){//找出左孩子和右孩子中較小的那個if (child+1 < n && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);//繼續向下調整parent = child; child = 2 * parent + 1;}else{break;}}
}//插入數據
void HeapPush(HP* php, HPDataType x)
{assert(php);//擴容if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;//插入新元素后,要使原來的堆還是小堆,就得向上調整AdJustUp(php->a , php->size-1);
}//打印數據
void HeapPrint(HP* php)
{assert(php);for (int i = 0; i < php->size; i++){printf("%d ", php->a[i]);}
}//刪除數據
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);//交換第一個和最后一個數據Swap(&php->a[0], &php->a[php->size - 1]);--php->size;AdJustDown(php->a, php->size, 0);
}//獲取第一個數據
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}//判斷是否為空
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}












【獨一無二】)





