5/25日參加了一個培訓分享會，由博奧研究院、武漢博奕咨詢和華工科技聯合舉辦，主題是“攜手Ai，共贏未來”。

抱著跟書友線下交流的心態我參與了，參與前我對博奧做了基礎了解，他們跟工信部考試和教育中心有合作，可以提供ai專項技能課程培訓，開始以為是想打廣告割韭菜，結果發現不是。現場座無虛席，博奧研究院總經理巖哥從頂層設計，國家政策規劃，ai發展趨勢，全程講解ai賦能，從元宇宙到數字人，再到實踐案例和產品演示，全面生動，干貨滿滿。培訓講師專業有溫度，介紹了國產多個ai工具的使用妙招，現引導操作，即時互動，有趣有料。



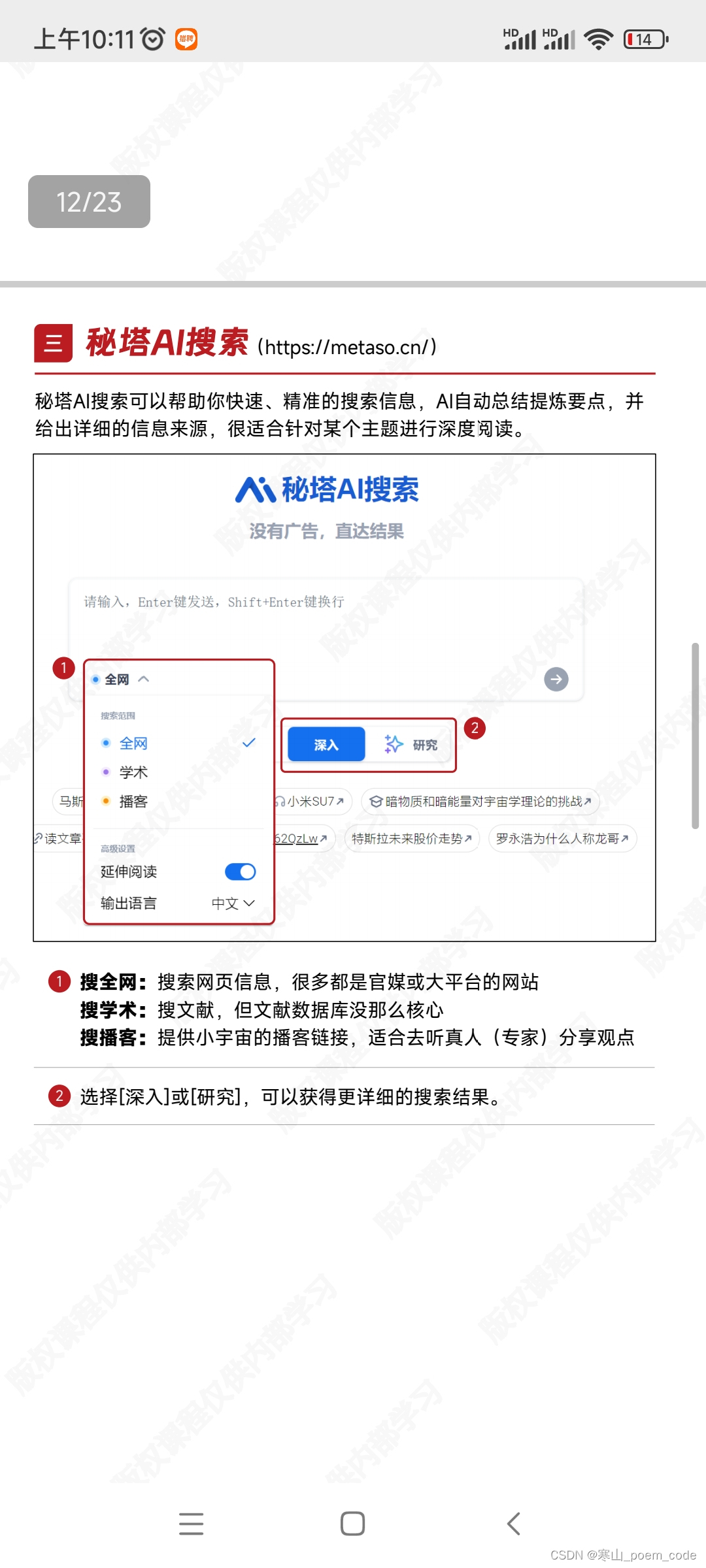
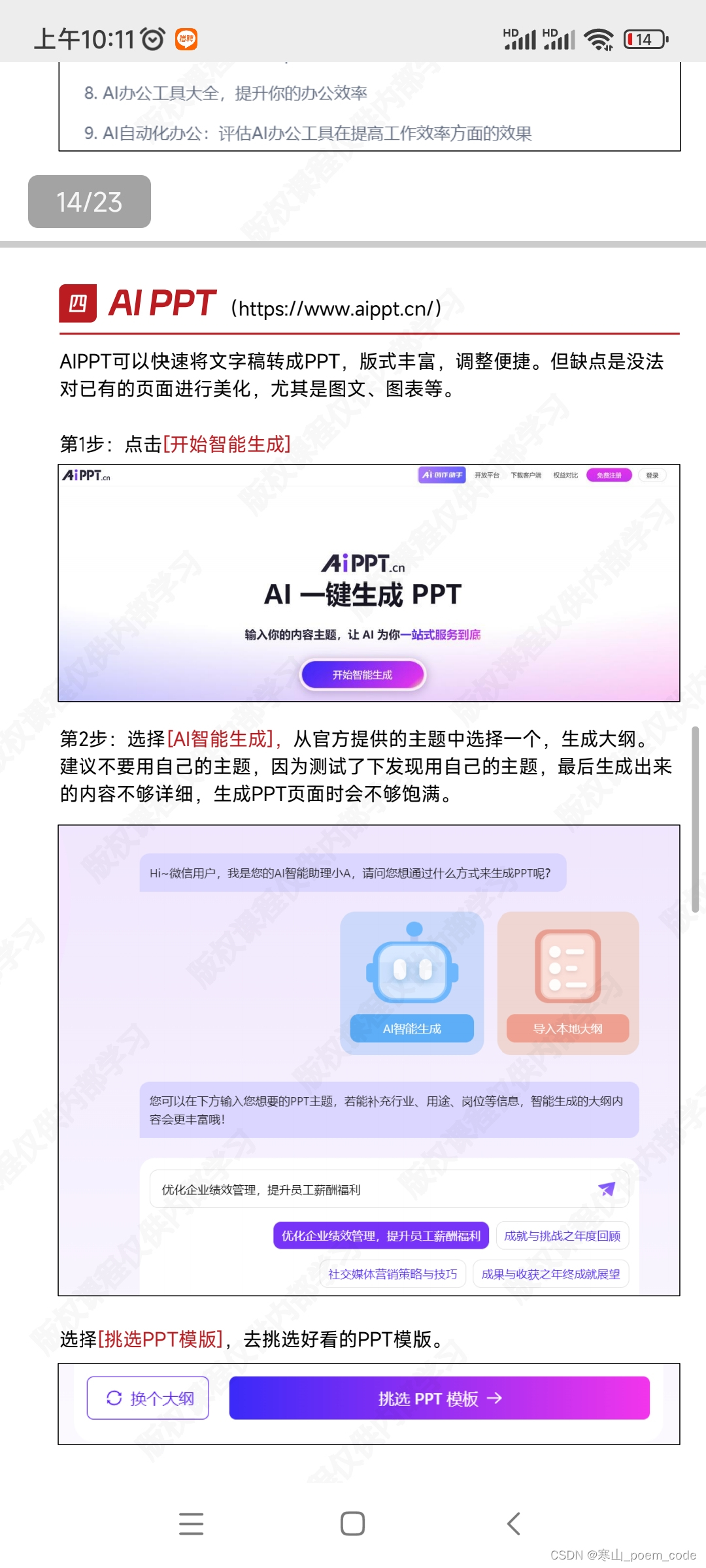
以上是部分圖片示例。

巖哥講完后，我趁著茶歇時間向他提了一個問題：會議主題是攜手ai，我大概明白啥意思，但是共贏未來，怎么共贏呢？
巖哥和華工科技的老師都做了回復，雖然沒有得到我想要的答案，確讓我受益匪淺。

我自己也總結了下對這個問題的思考：按層級分，國家層面大力支持ai發展，提出各種政策扶持。工信部和教育部層面制訂標準和人才培養考核措施，以及證書發放人才認證。培訓機構層面承上啟下，承接企業內訓，課程制訂，人才培養，等收費服務。企業層需要創新變革，引入培訓，通過運用ai賦能職場，新技術降本增效。職場層需要掌握ai工具的基礎使用，提升職場競爭力和晉升力。

至上而下，各方都有各自愿力，動機，訴求，需求，自此完美的閉環形成，可達成共贏局面。

個人的一點思考和總結，僅供參考。如需調整，請私信我，圖片來源于朋友圈和培訓交流群群內老師分享，侵刪。#猿腦2.0