
在深度學習中,神經網絡的初始化是一個看似不起眼,卻極其重要的環節。它就像是一場漫長旅程的起點,起點的選擇是否恰當,往往決定了整個旅程的順利程度。
今天,就讓我們一起深入探討神經網絡初始化的數學策略,以及這些策略對訓練的影響。
一、為什么要初始化?
當我們搭建好神經網絡模型,準備開啟訓練之旅時,權重和偏置的初始值就像是模型的“起跑線”。
如果起跑線設置得不合理,模型可能會陷入“跑不動”或者“跑偏”的困境。
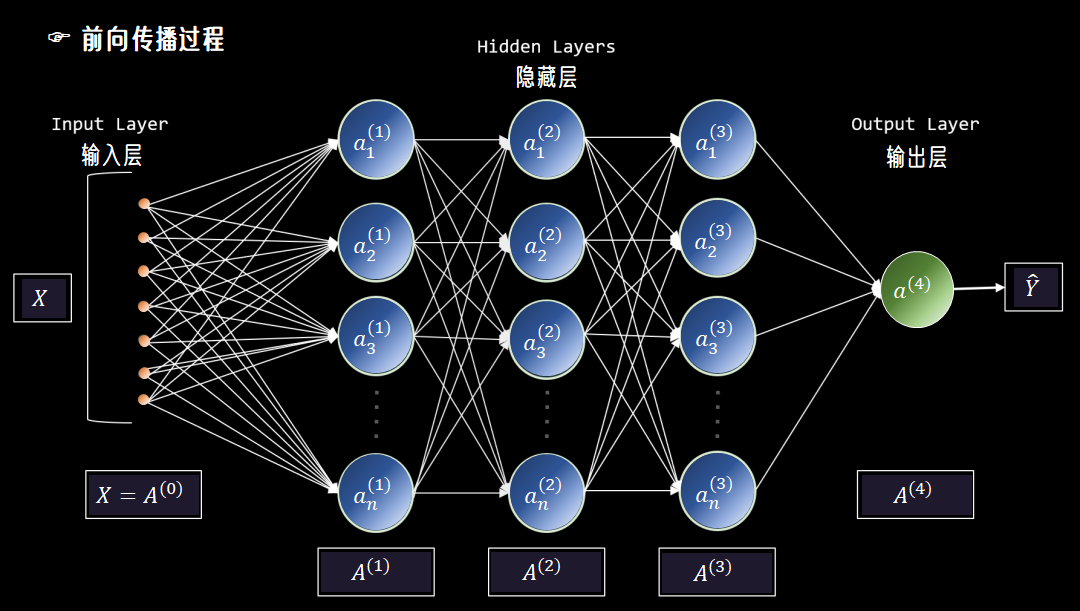
比如,如果所有權重都初始化為零。那么無論輸入是什么,每一層的輸出都會是相同的值,網絡的梯度也會消失,模型根本無法學習。
0m×n=(00?000?0????00?0)\mathbf{0}_{m \times n} = \begin{pmatrix} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \end{pmatrix}0m×n?=?00?0?00?0??????00?0??
而如果權重初始化過大,又會導致梯度爆炸,讓模型的訓練過程變得混亂不堪。
因此,合理的初始化是神經網絡訓練能夠順利進行的關鍵第一步。它不僅影響模型的收斂速度,還決定了模型是否能夠收斂到一個好的解。
二、權重初始化的方法
權重初始化是深度學習中一個重要的步驟,它對模型的收斂速度和最終性能有顯著影響。
以下是一些常見的權重初始化方法及其數學原理:
2.1 隨機初始化
隨機初始化是最直觀的一種方法。它的核心思想是給每個權重賦予一個隨機值,從而打破神經元之間的對稱性。
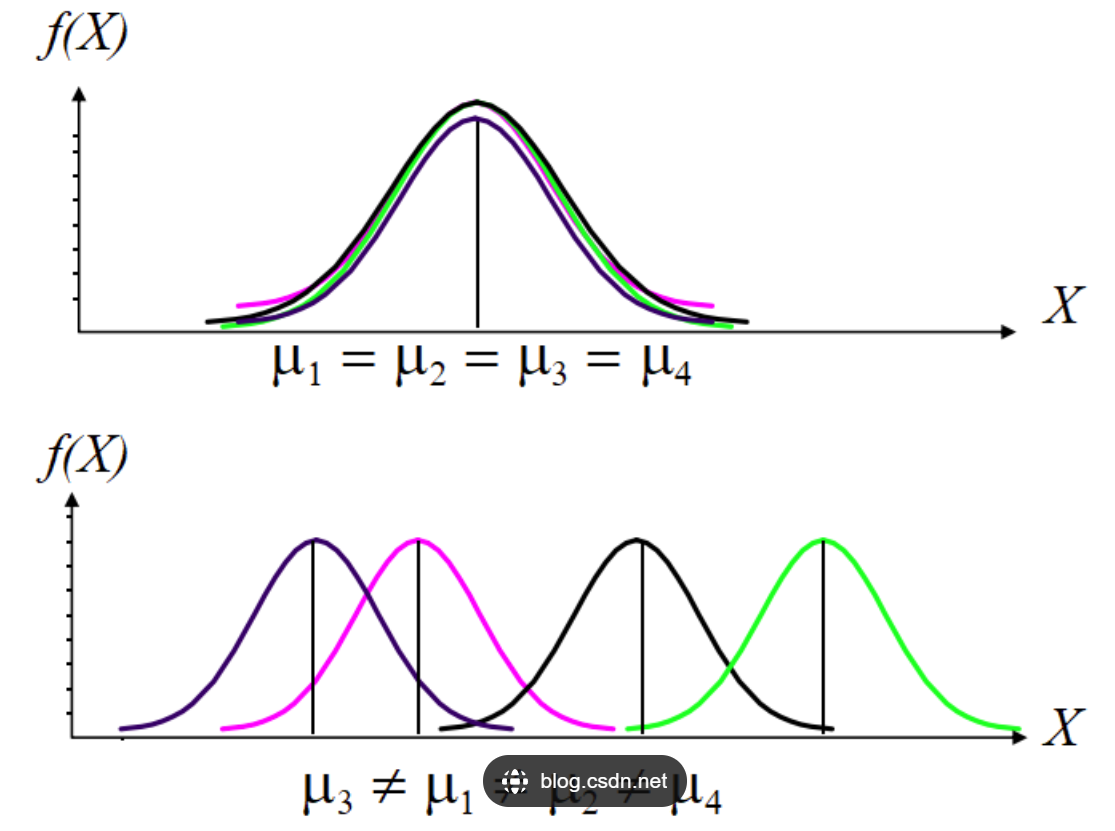
數學上,我們通常會從一個均勻分布或正態分布中隨機抽取權重值。
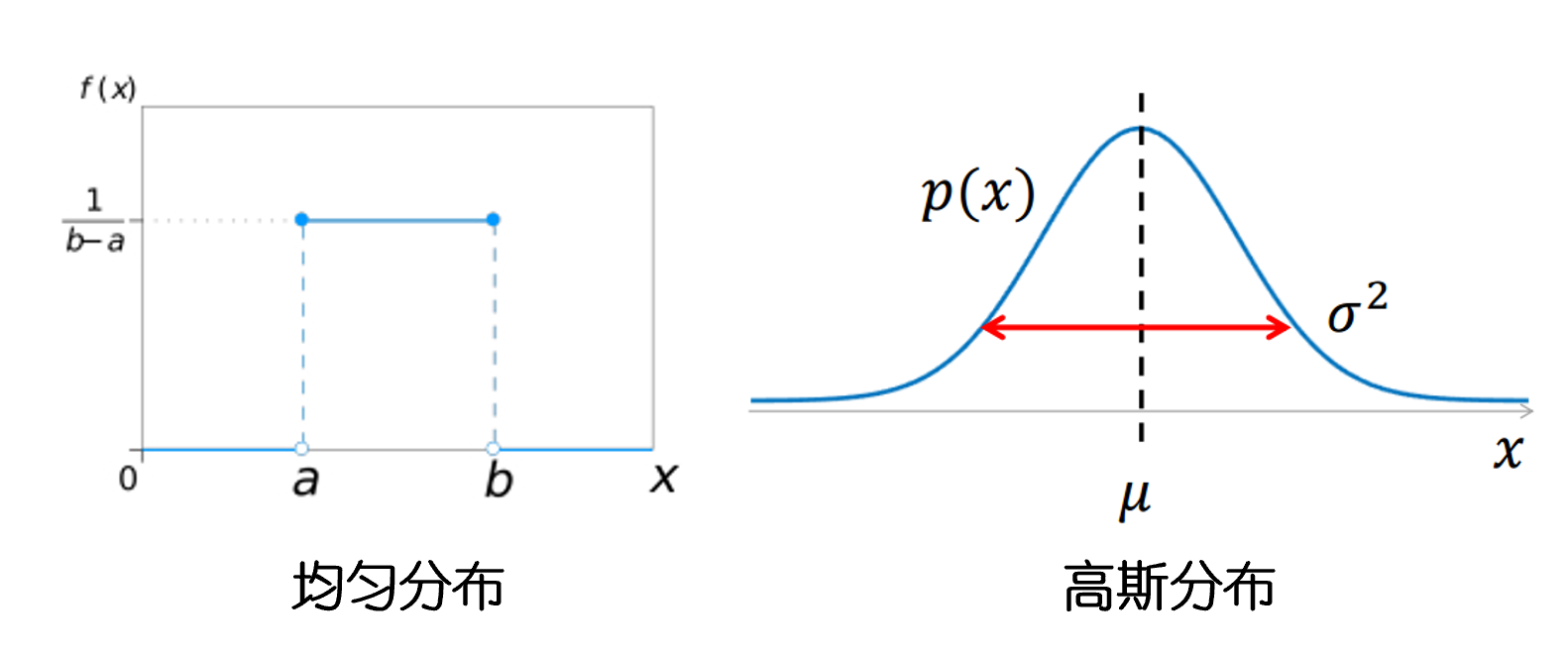
例如,我們可以使用均勻分布 U[??,?]U[-\epsilon, \epsilon]U[??,?],其中 ?\epsilon? 是一個很小的正數。<>
這樣做的好處是簡單直接,能夠讓神經元在初始階段就具有不同的激活值,從而避免了“所有神經元都一樣”的問題。
但如果?\epsilon?選擇得過大或過小,可能會導致網絡在訓練初期就出現梯度爆炸或梯度消失的問題。因此,我們需要還更精細的初始化方法。
2.2 Xavier初始化
Xavier初始化是一種針對激活函數為Sigmoid或Tanh的網絡設計的初始化方法。其核心思想是保持輸入和輸出的方差一致,從而避免梯度消失或爆炸。
假設輸入的方差為 Var(x)\text{Var}(x)Var(x),權重的方差為 Var(w)\text{Var}(w)Var(w),那么對于一個神經元的輸出 y=w?xy = w \cdot xy=w?x,其方差可以表示為:
Var(y)=Var(w)?Var(x)\text{Var}(y) = \text{Var}(w) \cdot \text{Var}(x)Var(y)=Var(w)?Var(x)
為了保持輸入和輸出的方差一致,我們需要讓 Var(y)=Var(x)\text{Var}(y) = \text{Var}(x)Var(y)=Var(x)。因此,Xavier初始化將權重的方差設置為:
Var(w)=1n\text{Var}(w) = \frac{1}{n}Var(w)=n1?
其中 nnn 是前一層的神經元數量。
這樣,無論網絡有多深,每一層的方差都能保持一致,也就避免了梯度消失或爆炸的問題。
2.3 He初始化
He初始化是一種針對ReLU激活函數設計的初始化方法。
He初始化的核心思想是調整權重的方差,使其更適合ReLU激活函數。
具體來說,He初始化將權重的方差設置為:
Var(w)=2n\text{Var}(w) = \frac{2}{n}Var(w)=n2?
其中nnn仍然是前一層的神經元數量。
這個公式比Xavier初始化多了一個2,是因為ReLU激活函數在訓練初期更容易產生較大的梯度。通過這種方式,He初始化能夠更好地平衡ReLU激活函數的特性,避免梯度爆炸的問題。
三、偏置初始化的策略
與權重初始化相比,偏置初始化相對簡單一些。一般來說,偏置可以初始化為零或一個很小的常數。
在大多數情況下,將偏置初始化為零已經足夠了。然而,對于某些特定的激活函數,如ReLU,將偏置初始化為一個很小的正數可能會更有幫助。
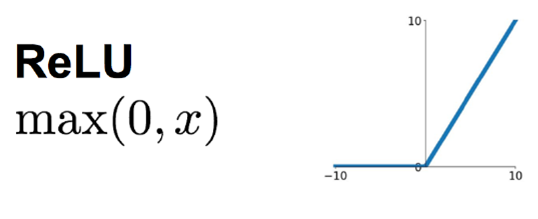
這是因為ReLU激活函數在輸入為負時輸出為0,這可能會導致一些神經元在訓練初期就“死亡”,即它們的輸出始終為0。
通過將偏置初始化為一個很小的正數,可以增加神經元的初始輸出,從而避免它們過早死亡。
神經網絡的初始化是一個看似簡單卻極其重要的環節。通過精心設計權重和偏置的初始化策略,我們可以有效地避免梯度消失或爆炸的問題,從而讓網絡在訓練過程中能夠快速收斂,并且具有更好的穩定性。
在實際應用中,我們需要根據網絡的結構和激活函數的特性,選擇合適的初始化方法。例如,對于使用Sigmoid或Tanh激活函數的網絡,Xavier初始化是一個不錯的選擇;而對于使用ReLU激活函數的網絡,He初始化則更為合適。
注:本文中未聲明的圖片均來源于互聯網




![[rStar] 搜索代理(MCTS/束搜索)](http://pic.xiahunao.cn/[rStar] 搜索代理(MCTS/束搜索))



)





 D題題解記錄)




